Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

In questa serie di articoli, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti. Nel primo di essi, parliamo di qualcosa che tutti dovrebbero conoscere: gli elementi orbitali. Tuttavia, vedremo che la determinazione degli elementi orbitali non permette di ricavare immediatamente la posizione di un pianeta nella sua orbita. La faccenda è piuttosto complicata e ha dato non pochi grattacapi allo stesso Keplero, che l’ha però affrontata e risolta con una sapienza a dir poco inaspettata per i suoi tempi.

L’orbita di un pianeta, di un satellite naturale o di un satellite artificiale può essere definita in vari modi. Noi consideriamo quello classico, usato normalmente per i pianeti e i corpi minori del Sistema Solare. Alcune misure angolari cambiano quando si parla dei satelliti dei pianeti e delle comete. I parametri che definiscono un’orbita vengono chiamati elementi orbitali.

Innanzitutto, va tenuto presente che nessun corpo planetario ha degli elementi orbitali fissi, dato che essi variano continuamente per effetto delle perturbazioni dei compagni di viaggio. In questo articolo ci riferiamo, quindi, ai parametri orbitali nel caso kepleriano, ossia nel problema dei due corpi. In altre parole, quelli relativi a un orbita ricavata dalla legge di gravitazione universale di Newton. Inoltre, essi si riferiscono a un sistema non-inerziale, ossia a un sistema relativo a uno dei due corpi, specificatamente il Sole (o il pianeta per i satelliti). In altre parole, essi vengono definiti considerando come fissa la posizione della massa principale (Sole o pianeta) e analizzando la traiettoria del secondo corpo intorno al primo. Sappiamo, infatti benissimo, che due corpi rivolvono, in realtà, attorno al baricentro del sistema.

Gli elementi orbitali necessari a definire un’orbita e, di conseguenza, a calcolare la posizione del corpo celeste in ogni momento (effemeridi) sono sei. Essi possono essere divisi in tre gruppi (o meglio quattro).

Il primo gruppo (due parametri) serve a definire la forma dell’orbita come si presenta sul proprio piano orbitale. Il secondo (due parametri) serve a definire l’orientamento del piano orbitale rispetto a un piano di riferimento (l’eclittica per i pianeti e il piano equatoriale per i satelliti). Il terzo gruppo (un parametro) definisce l’orientamento dell’orbita nel suo piano. Il quarto gruppo (un parametro) è molto particolare ed è quello che definisce la posizione dell’oggetto lungo la sua orbita. Si può facilmente notare che esso è il solo ad avere bisogno del tempo. Tutti gli altri definiscono soltanto la traiettoria, in cui il pianeta può anche non esistere, l’ultimo lo inserisce nella posizione che occupa realmente a un certo istante.

Dato che, come già detto, gli elementi orbitali variano col tempo, è necessario aggiungere un ulteriore parametro che indichi a quale data si riferiscono i parametri orbitali. Esso serve, in pratica, a stabilire con esattezza il sistema di riferimento usato. Alcuni lo considerano un “settimo” elemento, ma in realtà non ha niente a che fare con la descrizione kepleriana.

Iniziamo a definirli esattamente, utilizzando varie figure.

Il primo gruppo (Fig. 1) contiene i due parametri più conosciuti: semiasse maggiore a ed eccentricità e (vedi QUI). Il primo ci dice qualcosa sulla distanza media dal Sole (posto in un fuoco dell'ellisse) e il secondo quanto l’orbita sia allungata. Da essi si deducono subito due distanze estremamente particolari e molto usate: la distanza perielica q e la distanza afelica Q. La prima identifica il punto di minima distanza raggiungibile dal pianeta rispetto al Sole (perielio P) e la seconda il punto di massima (afelio A).

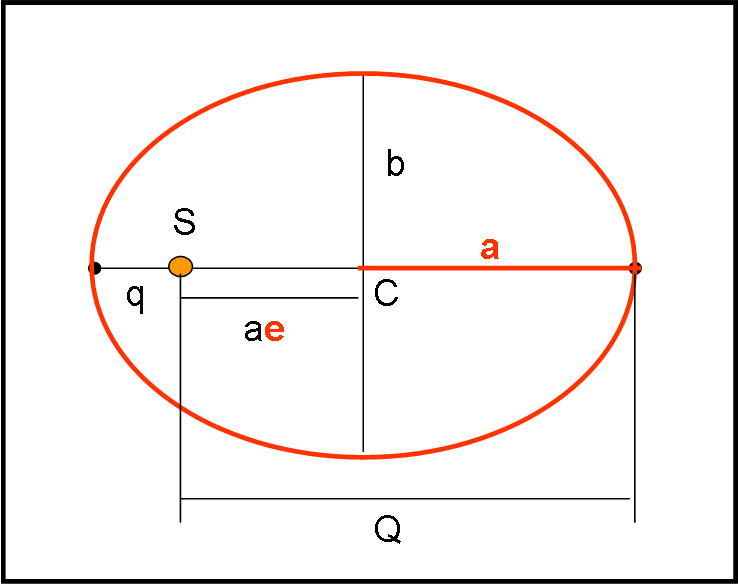
Le formule che permettono di ricavare queste due grandezze “ausiliarie” sono:

q = a(1 - e)

Q = a(1 + e)

Ovviamente, nel caso in cui e = 0, cadiamo nel caso di un’orbita circolare, con il Sole che si porta nel centro C e il semiasse che diventa il raggio della circonferenza. Perielio e afelio perdono di significato.

Il secondo gruppo (Fig. 2) è formato, innanzitutto, dall’inclinazione i del piano dell’orbita rispetto al piano dell’eclittica. Esso serve, immediatamente, a definire la linea dei nodi, ossia la linea intersezione tra i due piani (ne abbiamo parlato anche QUI). Nel suo moto di rivoluzione attorno al Sole, il pianeta passa da una parte all’altra della sfera celeste, centrata nel Sole,  rispetto al piano dell’eclittica. Il nodo ascendente N è quello che vede il passaggio del pianeta diretto verso l’alto. In N’ (nodo discendente) avviene il contrario: il pianeta scende verso il basso.

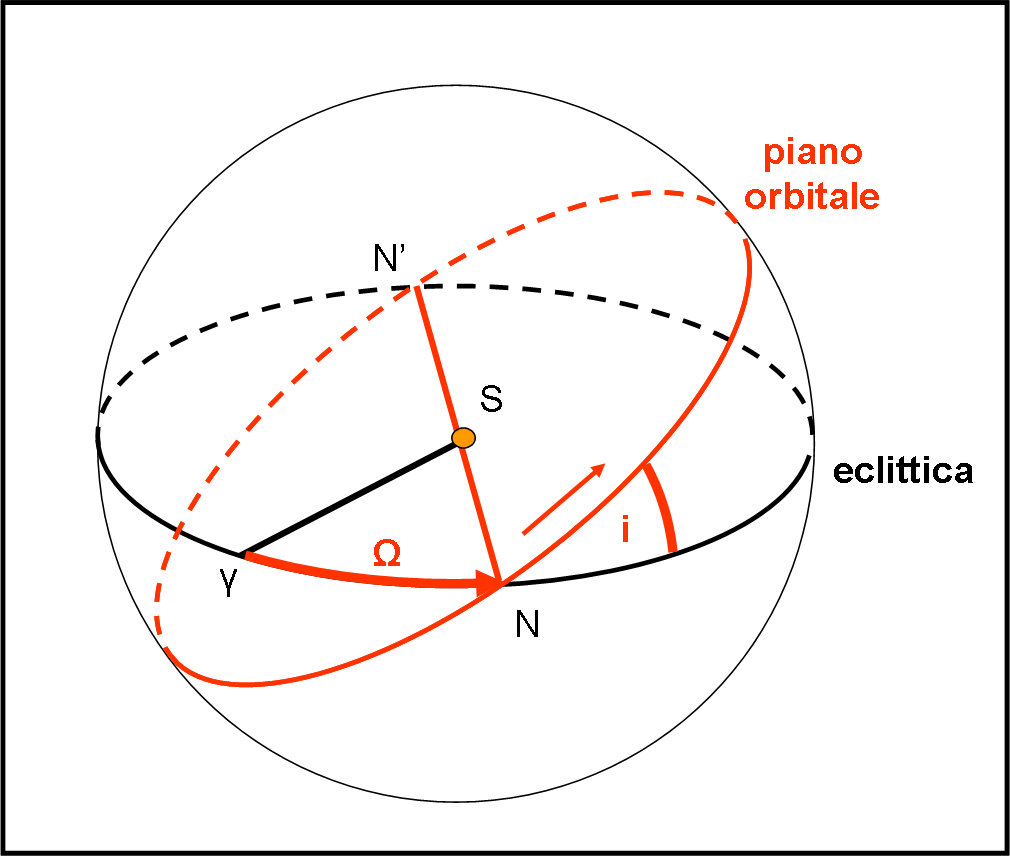
Definita una linea fissa sul piano dell’eclittica (si sceglie  la direzione del punto γ di cui parleremo a lungo nella trattazione dei sistemi di riferimento e che rappresenta la linea dei nodi tra piano dell'equatore terrestre ed eclittica) si definisce come longitudine del nodo ascendente  Ω l’arco di cerchio massimo γN (o -se preferite- l’angolo in S tra γ e N). Dell’arco di cerchio massimo abbiamo parlato nella lezione 3 della geometria sferica.

Con questi due parametri abbiamo piazzato in modo univoco il piano orbitale rispetto al piano di riferimento che è l’eclittica.

La forma dell’orbita è stata stabilita così come la posizione del piano orbitale rispetto all’eclittica. Non ci resta, adesso, che trovare la posizione dell’orbita sul suo piano orbitale. In poche parole, prendiamo una linea particolare dell’orbita e fissiamola rispetto a un'altra linea ben determinata della sua orbita. Queste due linee sono la linea degli apsidi, ossia la congiungente afelio-Sole-perielio (ossia quella che misura l’asse maggiore dell’ellisse) e la linea dei nodi determinata precedentemente. Siamo di nuovo in un problema piano.

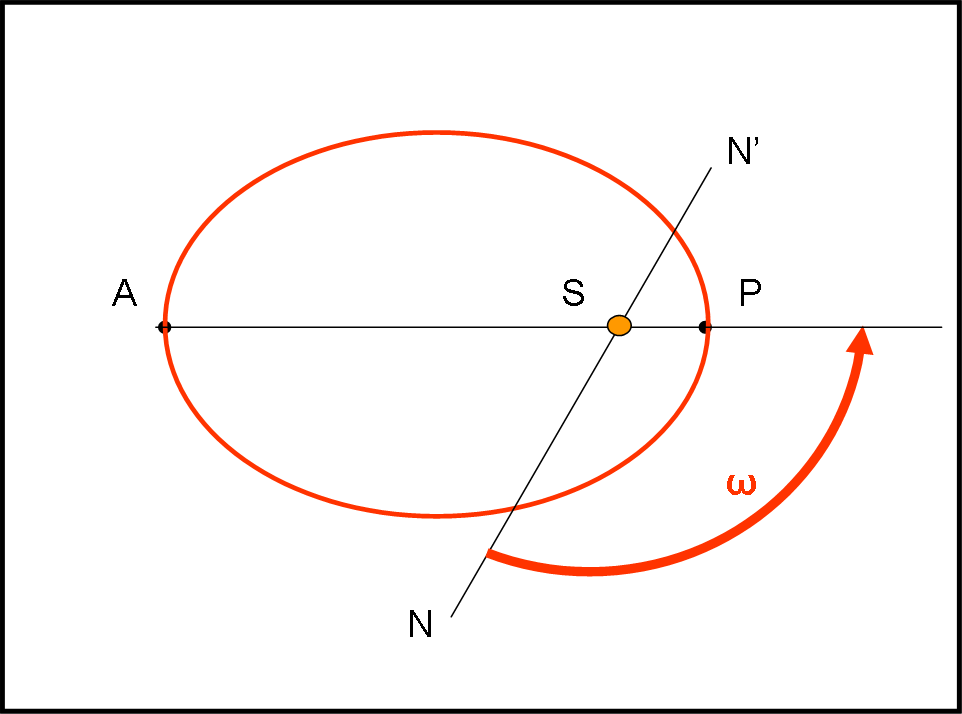
Il terzo gruppo (Fig. 3) è composto dall’angolo formato dalla direzione Sole-nodo ascendente e la direzione Sole-perielio, che viene chiamato argomento del perielio ω. A questo punto è come se avessimo incollato l’orbita (che ha una forma ben determinata) sul suo piano orbitale che a sua volta è stato bloccato univocamente rispetto all’eclittica.

La parte puramente geometrica si è conclusa e la riassumiamo nella Fig. 4.

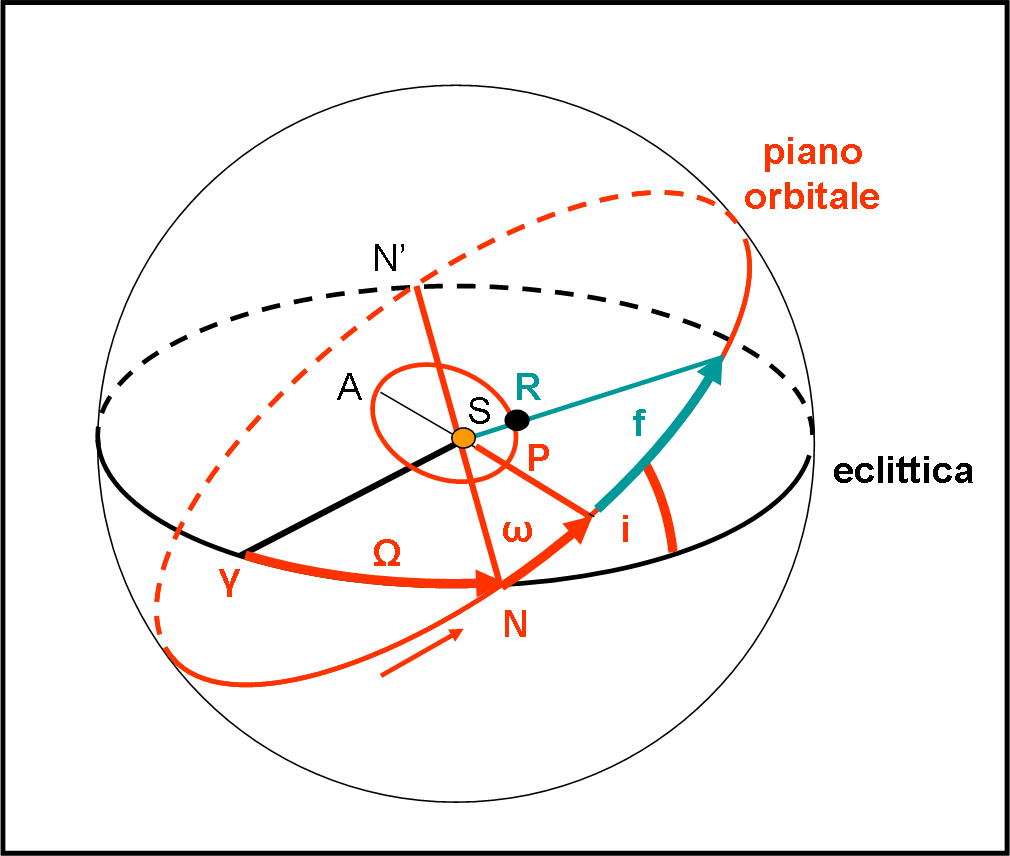
A questo punto non resta che inserire il vero pianeta nella sua orbita e vedere dove si trova.

Un modo per determinare questa situazione è quella di indicare il tempo in cui il pianeta passa al perielio e poi determinare la posizione attuale rispetto al perielio. Ciò comporta la conoscenza dell’angolo al Sole tra perielio e pianeta, ossia la conoscenza dell’angolo chiamato anomalia vera f.

In teoria, esso deriva direttamente dalla seconda legge di Keplero (la velocità areolare è costante), ma il suo calcolo effettivo è tutt’altro che semplice, da un punto di vista matematico. Esso, infatti, è un angolo che varia continuamente col tempo in modo non lineare (il pianeta cambia continuamente la sua velocità). E’ molto più conveniente usare un angolo “ausiliario” che vari linearmente col tempo e che sia legato all’anomalia vera. Un bel problemino che introduce un altro angolo ausiliario, ma che semplifica di molto il calcolo della posizione finale del pianeta.

Ne consegue che, invece di indicare il tempo di passaggio al perielio, si indica l’anomalia media M a una certa data e, attraverso di lei (che varia linearmente), si determina l’anomalia vera e la posizione reale del pianeta.

L’anomalia media è un angolo che non corrisponde a un effettivo angolo geometrico visibile in figura, per cui si preferisce sempre indicare l’anomalia vera (l’angolo VERO, appunto).

Il problema di passare dall’anomalia media, di facile calcolo, all’anomalia vera prende anche il nome di problema di Keplero, che lui riuscì a risolvere in modo geniale anche se abbastanza approssimato. Oggi, con i computer, la trasformazione è di irrisoria facilità.

 

Quanto detto spiega perché in molti testi si continui a dare come sesto elemento orbitale il tempo di passaggio al perielio, mentre invece si trova indicata l’anomalia media nei testi professionali che servono effettivamente a ricavare la posizione del pianeta a ogni istante.

Certi angoli vengono chiamati anomalie fin dall’antichità, dato che rappresentavano “anomalie” rispetto a un moto perfettamente circolare.

In realtà (come già accennato), la conoscenza degli elementi orbitali non permette una posizione del pianeta abbastanza accurata, dato che le perturbazioni degli altri pianeti li modificano continuamente e vari effetti a lungo periodo, come la precessione degli equinozi, sposta in maniera sensibile la direzione del punto γ. E’ per questo che gli elementi orbitali sono sempre accompagnati da un’epoca di riferimento attraverso la quale può essere calcolata facilmente la posizione di γ all’epoca attuale. In generale, comunque, la determinazione della posizione di un pianeta abbisogna della soluzione (più o meno accurata) del problema degli n corpi (risolvibile solo attraverso integrazioni numeriche).

Per determinare un’orbita approssimata o -meglio- kepleriana sono necessari sei parametri. Ciò vuol dire, matematicamente parlando, che abbiamo sei incognite. E’ necessario, perciò, determinare almeno sei equazioni in cui compaiano le sei incognite (in realtà, molte di più in modo da applicare il metodo dei minimi quadrati). Nei metodi “classici” bastavano tre posizioni e tre velocità, osservate da terra, per ottenere gli elementi orbitali. Oggi si usano metodi anche molto diversi. Tuttavia, il problema della determinazione degli elementi orbitali è, ormai, un lavoro di routine, effettuato, quasi automaticamente, in alcuni centri specializzati. Il volerli calcolare “in casa” è solo e soltanto un simpatico esercizio di ben poca utilità pratica. Analogo discorso vale per il problema opposto: passare dagli elementi orbitali alla posizione reale all’istante desiderato (calcolo delle effemeridi).

E’, invece, oltremodo interessante (non solo storicamente) descrivere meglio il legame tra anomalia media e anomalia vera, ossia andare a fondo del problema di Keplero. Sotto questo punto di vista, è più che giusto dare grande risalto all’anomalia eccentrica e all’equazione di Keplero, un piccolo grande capolavoro di meccanica, risolto prima ancora che questa disciplina nascesse realmente…

Ne consegue che, tanto per richiamare una nuova voce di Wikipedia, aggiunta da un nostro lettore, ha poco senso parlare singolarmente delle varie anomalie, ma è fondamentale trattarle tutte  assieme, per potere veramente comprendere il loro significato teorico e “pratico”. Ed è quello che faremo nel prossimo articolo. Vedremo che l’interesse non sarà trascurabile…

QUI trovate tutti gli articoli su “Gli elementi orbitali e i loro compari”

Chi ha voglia e curiosità di fare due chiacchiere con Keplero in persona (e non solo lui), può trovarlo QUI