Link al capitolo 1. Link al capitolo 2.

Nei precedenti capitoli avevamo visto che è enormemente probabile che l'entropia aumenti perché il sistema tenderà ad evolvere verso configurazioni macroscopiche che corrispondono ad un grande numero di configurazioni microscopiche con il conseguente emergere della freccia del tempo.

A questo punto dobbiamo introdurre il concetto di stato di un sistema fisico, ovvero tutte le informazioni relative al sistema ad un dato istante di tempo che è necessario specificare per determinarne l'evoluzione temporale, una volta assegnate le leggi della fisica. In meccanica classica, ad esempio, equivale a specificare la posizione e quantità di moto di ogni singola particella.

Con il termine microstato si indica lo stato preciso di un sistema. Il macrostato invece specifica solo le caratteristiche macroscopicamente osservabili. Pensiamo ad esempio al solito recipiente di gas diviso in due da una parete nella quale è praticato un foro, il microstato ad un certo istante è dato dalla posizione e dalla quantità di moto di ogni singola molecola di gas, mentre quello che noi osserviamo a livello macroscopico è solo quante molecole stanno nella parte destra e quante nella parte sinistra, cioè un macrostato.

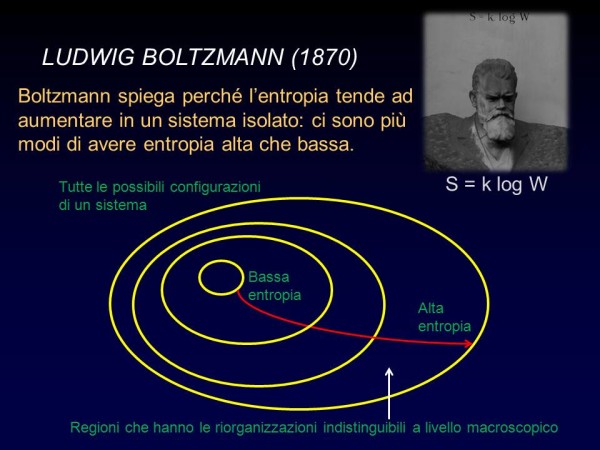
La definizione di W (entropia) diventa quindi, più brevemente: il numero di microstati corrispondenti ad un particolare macrostato.

Boltzmann, quindi, spiega in questo modo l'origine della freccia del tempo: partiamo da un insieme di leggi della fisica microscopiche che sono invarianti per inversione temporale, non distinguono tra passato e futuro. L'entropia caratterizza il numero di stati microscopici che a livello macroscopico sono indistinguibili e nella ragionevole ipotesi che il sistema tenda ad evolvere verso configurazioni macroscopiche che corrispondono ad un gran numero di stati possibili, è naturale che l’entropia cresca nel tempo.

La freccia del tempo, quindi, nasce perché l’Universo passa naturalmente da configurazioni rare a configurazioni più comuni col passare del tempo.

L’aumento dell’entropia è responsabile di tutti gli aspetti della freccia del tempo e rende possibile la vita.

La fonte principale di energia per la Terra è il Sole e come insegna Clausius il calore fluisce spontaneamente dal un corpo caldo ad un corpo freddo, ma se la storia finisse lì prima o poi i due corpi arriverebbero all'equilibrio termico e non succederebbe più nulla, perché sarebbe un mondo statico. Nell'Universo reale invece la Terra riceve energia dal Sole, la rielabora, e la irraggia nello spazio, che è molto più freddo della Terra, sotto forma di energia, nella stessa quantità, ma ad entropia 20 volte più elevata.

La vita è coerente col secondo principio della termodinamica. Ma cos'è la vita?

Schrodinger disse che un pezzo di materia è vivente quando va “facendo qualcosa”, si muove, scambia materiali con l’ambiente e così via, per un periodo di tempo più lungo di quanto ci aspetteremo in circostanze analoghe da un pezzo di materia inanimata. Gli organismi viventi mantengono l’ordine nel loro ambiente locale (che comprende anche il loro corpo) sfruttando l’energia utile e degradandola ad energia inutile.

Distinguiamo il passato dal futuro anche attraverso la relazione tra causa ed effetto, gli effetti comportano sempre un aumento di entropia, pensiamo ad un tuffatore che si tuffa in piscina, o quando, giocando a biliardo, spacchiamo una formazione di palle ordinatamente disposte a triangolo (provocando un visibile aumento di entropia).

Per capire il perché il secondo principio funziona nel nostro mondo reale non è sufficiente applicare il ragionamento statistico alle leggi fondamentali della fisica. Il secondo principio, nella definizione statistica di Boltzmann, non è una legge assoluta, ma descrive un comportamento che è oltremodo probabile. Se ad esempio partiamo da uno stato di entropia media, quasi tutti i microstati corrispondenti evolveranno verso un’entropia maggiore, ma un piccolo numero di essi si sposterà verso un’entropia minore.

Dobbiamo inoltre tenere conto del principio di indifferenza, secondo cui dato un certo macrostato, di cui conosciamo l’intero insieme dei microstati, possiamo presupporre che siano tutti ugualmente probabili. Questo principio fu studiato nel contesto della teoria della probabilità dal grande matematico francese Laplace, ed in sintesi dice che quando non esistono informazioni sufficienti a far preferire, su un determinato fenomeno, un'ipotesi rispetto ad un'altra, le probabilità ad esse associate sono equivalenti.  

Boltzmann ci ha spiegato perché l’entropia aumenta: ci sono più modi di avere entropia alta che bassa, dunque la maggior parte dei microstati che fanno parte di un macrostato a bassa entropia evolveranno verso macrostati ad entropia più alta. Ma questo ragionamento non fa alcun riferimento alla direzione del tempo. Seguendo quella logica, la maggior parte dei microstati all’interno di un dato macrostato si muoveranno verso una maggior entropia in futuro, ma saranno anche provenuti da condizioni di entropia maggiore in passato.

Nel mondo reale, in pratica, quando consideriamo i microstati all’interno del nostro macrostato non applichiamo il principio di indifferenza, scegliamo solo i microstati compatibili con un passato di entropia molto bassa.

Dobbiamo ipotizzare anche che l’Universo abbia avuto inizio in uno stato di entropia molto bassa. Questa ipotesi prende il nome di ipotesi sul passato, che rappresenta quindi una eccezione al principio di indifferenza.

Un esempio di ricorso all’ipotesi sul passato è quella dei ricordi, ovvero la possibilità che abbiamo di ricordare il passato, spiegata in termini di entropia. Pensiamo ad esempio ad una nostra fotografia del decimo compleanno che ci ritrae con un maglione rosso. Se non facessimo ricorso all'ipotesi sul passato potremmo dire con assoluta certezza che alla festa dei nostri dieci anni indossavamo un maglione rosso? La risposta è no. La storia che raccontiamo per spiegarla (una elaborata ricostruzione del passato, la festa di compleanno, una fotografia che si conserva per molti anni, ecc…) è ancor meno probabile della foto in sé, intesa come una fluttuazione casuale di atomi proveniente da uno stato di entropia maggiore. In pratica non applichiamo il principio di indifferenza al macrostato attuale del mondo, che ci imporrebbe di assegnare a tutti i microstati la stessa probabilità, ma consideriamo solo quei microstati che sono compatibili con un passato ad entropia molto bassa.

Un altro esempio: immaginiamo di camminare lungo una strada e di notare sul marciapiede un uovo rotto; la nostra presunzione di bassa entropia del passato ci consente di affermare con elevata sicurezza che non molto tempo fa ci deve essere stato un uovo integro, che qualcuno ha lasciato cadere. Poiché non vi è ragione di sospettare che l’entropia diminuirà nel futuro, non possiamo dire molto circa il futuro dell’uovo, ci sono troppe possibilità: forse rimarrà lì e marcirà, forse qualcuno lo leverà e pulirà il marciapiede, forse lo mangerà un cane… quell'uovo sul marciapiede è come un ricordo nel nostro cervello.

Tutto questo però implica una questione che tutt'ora non è stata risolta ed è oggetto di controversie, ovvero se ci sono più modi di avere alta entropia che bassa, perché ieri l’entropia era più bassa? L’entropia ieri era più bassa perché l’altro ieri era ancora più bassa, così come il giorno prima e via dicendo… Tutto questo ci porta a circa 13,7 miliardi di anni fa, all'epoca del Big Bang.

(continua...)