Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Quanto detto nel capitolo precedente esprimiamolo attraverso la Fig. 9.

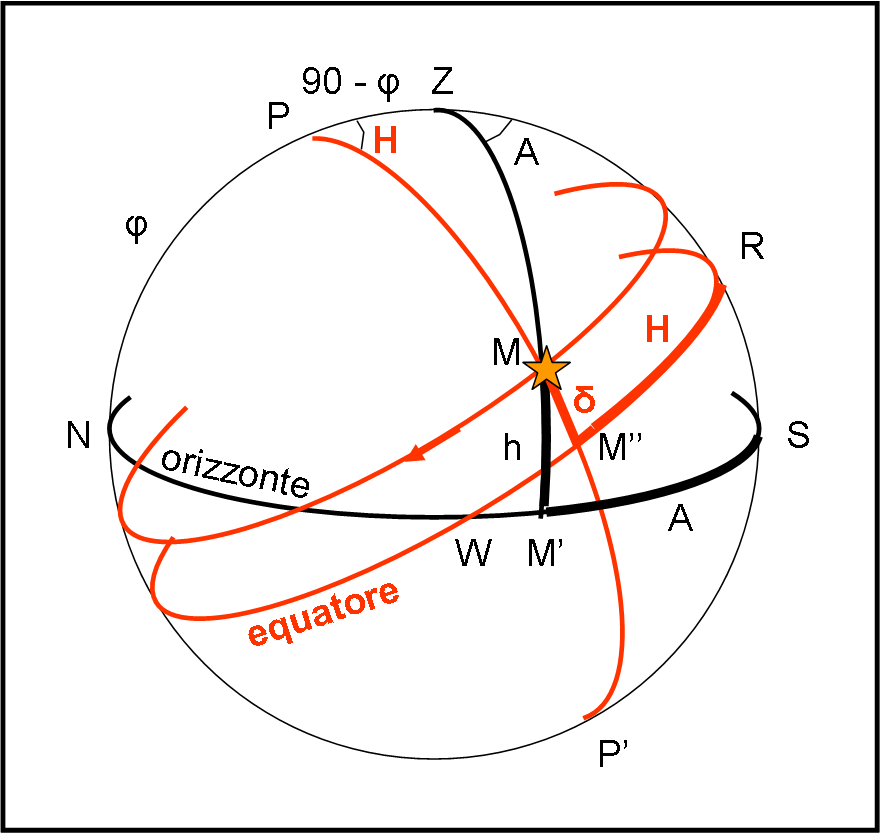
Disegniamo la sfera celeste ponendo sempre l’orizzonte celeste come cerchio massimo orizzontale. Sul cerchio massimo verticale (meridiano), segniamo lo zenit Z e il polo P, Come già sappiamo l’arco PZ è uguale a 90 – φ. E’ immediato tracciare il cerchio massimo che è definito dall’intersezione della sfera celeste con il piano dell’equatore terrestre, ossia l’equatore celeste. Diamo qualche definizione: tutti i cerchi massimi che passano per il polo P (e P’) sono chiamati cerchio orari. Quello tra essi che passa anche per Z è ovviamente il meridiano.  Le intersezioni di esso con l’orizzonte sono, di conseguenza, i punti N e S (come già visto nel primo sistema).

Dimostriamo subito che i punti intersezione tra orizzonte celeste ed equatore celeste sono i punti W ed E. Infatti, come punto dell’orizzonte il punto W (oppure E) è a 90 ° da Z. Tuttavia, come punto dell’equatore è a 90° da P. Ma se è a 90° da  P e Z deve essere a 90° da tutti i punti del cerchio massimo che passa per P e Z e, quindi, anche da N e S.

Come abbiamo visto nella Fig. 8 del capitolo precedente, le stelle appaiono muoversi da Est verso Ovest lungo cerchi minori paralleli all’equatore celeste (in modo simile ai paralleli terrestri). Nel loro moto apparente devono prima o poi attraversare il meridiano del luogo (il cerchio massimo PZ). Anzi, lo devono fare due volte, una ogni 12 ore. Quando la stella effettua questo passaggio alla massima altezza  il punto rappresenta la culminazione superiore. Dalla parte opposta, si ha la culminazione inferiore, che può  anche avere altezza negativa, ossia avvenire sotto l’orizzonte e quindi non essere visibile.

E’ immediato definire la prima coordinata in questo sistema: l’arco compreso tra il cerchio descritto dalla stella M e l’equatore (con segno più se è nell’emisfero nord e con segno meno se è nell’emisfero sud). Essa prende il nome di declinazione ed è una coordinata che non dipende assolutamente dal luogo dell’osservatore e dall’istante dell’osservazione. Ovviamente, essa può variare se la stella non è una stella, ma un corpo planetario o un satellite artificiale.

L’altra coordinata è invece più “ballerina”. Essa è l’angolo sferico ZPM o, se preferite, l’arco di equatore RM”, contato in ore minuti e secondi a partire dal meridiano, in senso positivo verso W e negativo verso E. Prende il nome di angolo orario e vale 0^h quando la stella si trova alla culminazione superiore e 12^h quando è alla culminazione inferiore. Dato che la stella si muove continuamente, l’angolo orario è una coordinata che cambia da istante a istante, ma lo fa in modo costante (per quanto è costante la rotazione della Terra).

Si può notare, come già accennato, il grande vantaggio di questo sistema rispetto al primo. Una delle due coordinate che identificano una stella è uguale per tutti gli osservatori, dato che la distanza angolare tra equatore e cerchio minore a lui parallelo, che passa per la stella, deve rimanere sempre la stessa. Il cerchio minore descritto dalla stella prende anche il nome di parallelo di declinazione. E’ la stessa cosa che capita per i paralleli terrestri: due luoghi hanno sempre la stessa latitudine φ, indipendentemente da come orientate la Terra nello spazio. L’altra coordinata varia, ma in modo costante e basta un motorino per permetterci di seguire il moto di una stella nel cielo. Questo sistema è quello su cui si basano i telescopi a montatura equatoriale.

Finita la semplice descrizione, ci si pone un problema di grande importanza astronomica: conoscendo le coordinate di una stella nel primo sistema come si fa passare alle sue coordinate nel secondo sistema ( e viceversa)?

Potrei lasciarlo come esercizio per voi, dato che ormai dovreste conoscere perfettamente le formule fondamentali della trigonometria sferica (ecco che diventano utili!). Per non creare subito confusione, eseguiamo insieme la prima trasformazione e poi… vedremo.

Qual è il problema da risolvere? Conosciamo le coordinate h (altezza sull’orizzonte), oppure z (distanza zenitale) e l’azimut A di una certa stella S, definiti nel prima sistema. Entrambe sono coordinate variabili sia nel tempo che da luogo a luogo. Vogliamo determinare le coordinate δ (declinazione) e H (angolo orario),definite dal secondo sistema, dove la prima è una costante sia rispetto al tempo che al luogo, mentre la seconda varia col tempo in modo costante. In altre parole più sintetiche:

Dal primo al secondo sistema

La figura da utilizzare è nuovamente la Fig. 9, che riportiamo per comodità.

Il triangolo da cui dobbiamo partire è PZM. Innanzitutto… è un triangolo sferico? Sicuramente sì, dato che tutti i suoi lati sono archi di cerchio massimo (non dimentichiamoci mai questa verifica!), lo abbiamo spiegato QUI figura 6.  Se è un triangolo sferico, gli si possono applicare le formule fondamentali.  Definiamo bene ciò che conosciamo. Innanzitutto l’arco PZ, che 90° - φ, dove φ è la latitudine del luogo (coordinata terrestre che deve essere conosciuta da ogni cittadino, astrofilo oppure no). Conosciamo, poi, l’arco ZM che non è altro che la distanza zenitale z (o, se preferite, 90° - h). Conosciamo anche l’arco di cerchio massimo NM descritto sull’orizzonte. Esso vale 180° - A. Ma esso è anche uguale all’angolo PZM. Ovviamente, vogliamo determinare:

δ = 90° - PM

e

H = ZPM = arco sull’equatore M”R

In parole povere, conosciamo due lati e l’angolo tra essi compresi: PZ, ZM e PZM.

Non ci resta che applicare la prima formula fondamentale della trigonometria sferica (andate a cercarla QUI, dove l’abbiamo ricavata). Essa dice proprio che il coseno di un lato è uguale al prodotto dei coseni degli altri due lati più il prodotto dei loro seni moltiplicati per il coseno dell’angolo opposto al lato da determinare. In parole matematiche:

cos PM = cos PZ cos ZM + sen PZ sen ZM cos PZM

Tutto ciò che compare al secondo mebro è, però, conosciuto! Il coseno del primo membro è, invece, proprio il coseno di PM che è legata strettamente con una delle incognite, ossia la declinazione δ.

Sostituiamo i valori è otteniamo:

cos (90 – δ) = cos (90 – φ) cos z + sen (90 - φ) sen z cos (180 – A)

Ossia:

sen  δ = sen φ cos z – cos φ sen z cos A    …. (1)

ricordando che cos (180 – A) = - cos A  (al limite, andate a ripassarvi le basi della trigonometria QUI, capitolo 22)

La (1) è più che sufficiente per determinare δ, dato che il suo seno è positivo per δ positivo e negativo per δ negativo. In poche parole, la (1) ci basta per sapere se la declinazione è positiva o negativa.

Passiamo, adesso, alla determinazione di H.

Usiamo lo stesso triangolo di prima, ma utilizziamo la seconda formula fondamentale, quella dei seni, che ci dice che il rapporto tra i seni degli angoli e dei lati opposti è costante.

Nel nostro caso:

sen PZM/sen PM = sen ZPM/sen ZM

Sostituendo, abbiamo:

sen (180 – A)/sen (90 – δ) = sen H/sen z

sen A/cos δ = sen H/sen z

sen H = sen A sen z/cos δ        …. (2)

Dato che la declinazione δ è già stata ricavata, essa è adesso un valore conosciuto e quindi sembrerebbe che la (2) ci regali l’angolo orario H.

In realtà non è così, dato che il seno di un angolo che può andare da 0° a 180° (o da 0^h a 12^h, cosa del tutto analoga). Vediamo cosa dice allora la conoscenza di un angolo di questo tipo, attraverso il solito cerchio goniometrico di Fig.10.

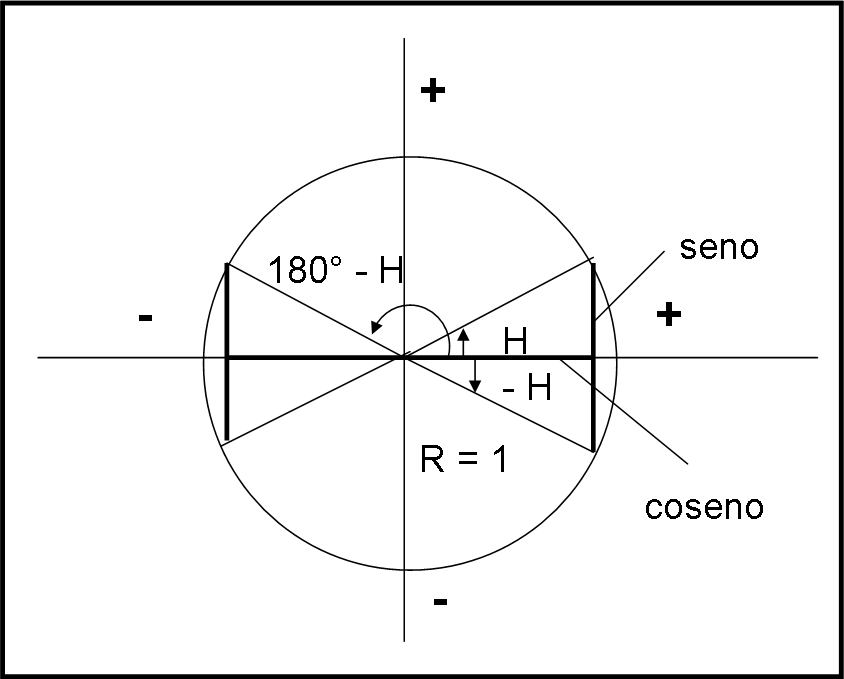
Come si vede molto bene, conoscere il sen H non riesce a dirci se H è proprio H o è 180 – H, dato che i loro seni sono uguali anche nel segno. In altre parole la (2) permette due soluzioni.

Potremmo, allora utilizzare nuovamente la prima formula fondamentale scrivendo:

cos ZM = cos PZ cos PM + sen PZ sen PM cos ZPM

cos z = cos (90 – φ) cos (90 – δ) + sen (90 – φ) sen (90 – δ) cos H

cos z = sen φ sen δ + cos φ cos δ cos H

da cui:

cos H = (cos z - sen φ sen δ)/ cos φ cos δ      …. (3)

Il secondo membro è conosciuto e quindi si ricava H. Ma siamo proprio sicuri? Il coseno di H e di 180 – H cambia di segno e quindi permette di determinare l’angolo giusto attraverso il suo segno. Tuttavia, il coseno di H e –H rimane lo stesso e noi sappiamo che H può assumere valori negativi. Accidenti nemmeno la (3) ci dona il risultato definitivo!

Attenzione, però… noi abbiamo determinato sia il seno che il coseno dell’angolo e quindi confrontando i loro due segni è immediato sapere in che quadrante cadono nel cerchio goniometrico. L’angolo H, quindi, è completamente risolto, utilizzando la (2) e la (3).

In realtà, in giro per il web si potrebbero trovare dei passaggi che portano a determinare la tangente degli angoli, ma per noi è più che sufficiente questa trattazione: più immediata e senza troppi passaggi.

Tanto per fare esercizio, dimostriamo che il coseno di H può essere anche ricavato con la terza formula fondamentale.

Essa dice, applicata al solito triangolo:

sen PM cos ZPM = cos ZM sen PZ – sen ZM cos PZ cos PZM

sostituendo:

sen (90 – δ) cos H = cos z sen (90 – φ) - sen z cos (90 – φ) cos (180 – A)

cos δ cos H = cos z cos φ + sen z sen φ cos A

cos H = (cos z cos φ + sen z sen φ cos A)/ cos δ        …. (4)

Anche nella (4) l’unica incognita è H e quindi può essere usata al posto della (3). Decidete voi quale preferite…

Dal secondo al primo

Ciò vuol dire, conoscere δ e H (e φ, ovviamente) e ricavare z (o h) e A.

Utilizziamo sempre la  Fig. 9.

Consideriamo sempre il triangolo sferico PZM. Questo volta, però, conosciamo δ e H, oltre che al solito φ. Dobbiamo ricavare l’altezza h (o la distanza zenitale z) e l’azimut A.

Ragioniamo un attimo… Del solito triangolo conosciamo due lati e l’angolo compreso. E’ quindi facile utilizzare la prima formula fondamentale per determinare il lato opposto all’angolo:

cos ZM = cos PM cos PZ + sen PM sen PZ cos ZPM

Sostituiamo:

cos z = sen δ sen φ + cos δ cos φ cos H          …. (5)

La coordinata z può variare tra 0 e 90° e tra 0 e – 90°. Ma, in entrambi i casi, il coseno risulta positivo. Abbiamo quindi bisogno di conoscere anche il seno di z. La faccenda si complica un po’, dato che qualsiasi altra relazione si possa applicare fa comparire entrambe le incognite (A e z).

Con grande pazienza, proseguiamo comunque…

La seconda formula fondamentale ci dice:

sin z/sen H = sin (90 – δ)/sin (180 – A) = cos δ/sin A

sen z sen A = sen H cos δ             …. (6)

La terza formula fondamentale dice invece:

sen z cos (180 – A) = cos (90 – δ) sen (90 – φ) – sen (90 – δ) cos (90 – φ) cos H

- sen z cos A = sen δ cos φ – cos δ sen φ cos H

Cambiando di segno:

sen z cos A = - sen δ cos φ + cos δ sen φ cos H       … (7)

Basta, adesso, dividere la (6) per la (7) e ci accorgiamo che il sen z si semplifica. Senza fare troppo calcoli è facile capire che ci troveremo di fronte alla tan A che per la stessa definizione di tangente ci permette di sapere in che quadrante cade l’angolo (A può variare tra 0 e 180 e  0 e -180).

Ricavato A, basta usare la (6) per determinare la z.

Tuttavia, nei casi pratici è ben difficile aver bisogno delle coordinate nel primo sistema a partire da quelle del secondo…

Possiamo tranquillamente passare al terzo sistema, forse il più conosciuto e usato. La vera e propria carta d’identità di una stella.

QUI trovate tutti gli articoli su questo argomento