Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Capisco benissimo che l’argomento che andiamo a trattare possa sembrare uno di quei noiosi e inutili procedimenti geometrici e matematici. Tuttavia, vi invito a non pensarla così e a dedicargli un poco del vostro tempo. Il pensare che Keplero sia stato in parte fortunato e in parte “brutalmente” empirico nella determinazione delle sue leggi è assolutamente falso. A parte l’aver saputo sfruttare al meglio le fantastiche osservazioni di Tycho Brahe, è indubbio che solo un uomo di eccezionale intuizione e di grande capacità di sintesi poteva arrivare al risultato ottenuto. La strada a Newton non poteva essere preparata meglio.

La sua grandezza è ulteriormente confermata da quello che viene riportato in questo articolo. La relazione tra l’angolo teoricamente fondamentale (anomalia vera) e gli angoli quasi astratti utilizzati da Keplero è un capolavoro di genialità e, quindi, di semplicità. Se pensiamo che è stato realizzato ben prima che nascesse la meccanica celeste, esso acquista un valore enorme sia dal punto di vista storico che pratico. Ancora oggi si utilizza comunemente, anche se sveltito in modo impressionante dai calcolatori elettronici.

Gustiamolo per quello che è e diamo a Keplero un valore che supera sicuramente l’apparente empirismo delle tre leggi. In conclusione: non perdetelo e seguitelo attentamente, sarà un vero regalo per delle menti che desiderano apprendere e capire l’armonia e l’eleganza della matematica e della meccanica, il linguaggio essenziale per vivere nel Cosmo con umiltà e orgoglio.

Anomalia eccentrica

La volta scorsa (QUI) abbiamo definito gli elementi orbitali, ponendo particolare attenzione sul tempo di passaggio al perielio e, di conseguenza, sul calcolo dell’anomalia vera f, ossia sulla determinazione della posizione del corpo planetario lungo la sua orbita. Abbiamo visto che la seconda legge di Keplero potrebbe risolvere la questione, ma che, in realtà, il calcolo sarebbe oltremodo complesso e si preferisce introdurre al posto di f degli angoli ausiliari. Questo procedimento prende proprio il nome di problema di Keplero.

Cominciamo con lo scrivere la seconda legge di Keplero, ricordando ciò che dice: le aree descritte dal raggio vettore (congiungente Sole-pianeta) sono proporzionali ai tempi impiegati a descriverle. Facciamo riferimento alla Fig. 5.

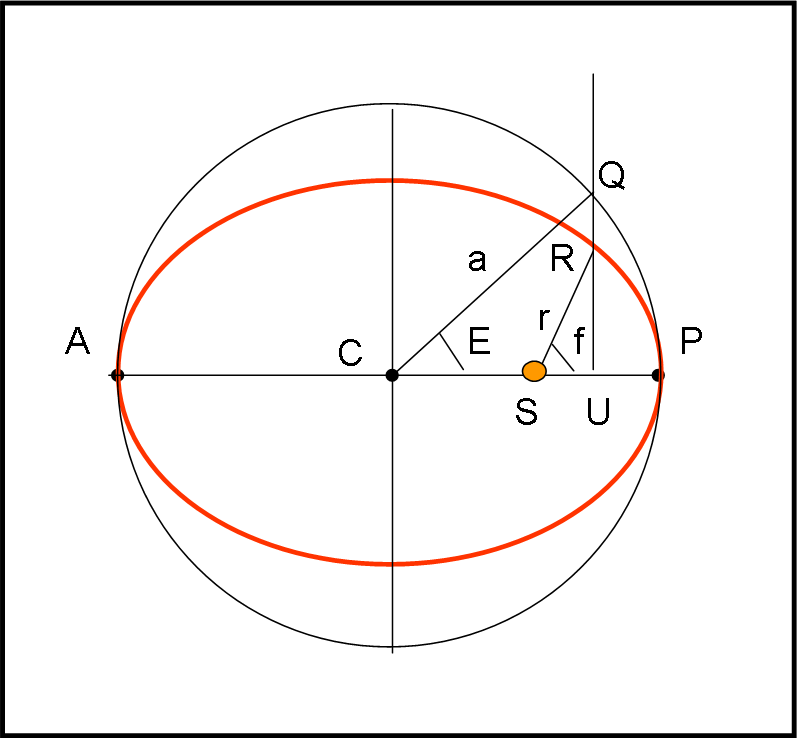
Ciò vuole anche dire che l’area dell’intera ellisse sta all’area descritta da SR come il periodo orbitale P sta al tempo trascorso dal passaggio al perielio al tempo relativo alla posizione R. In parole più sintetiche:

Area (SRP)/πab = (t – t₀)/P              ( a e b semiassi dell’ellisse)

Area (SRP) = πab(t – t₀)/P

Come già detto, il secondo membro è noto e dall’area si potrebbe dedurre la posizione di R. Ma, il calcolo è complesso e Keplero si mise all’opera…

Introduciamo la grandezza moto medio n, dato da:

n = 2π/P

che non è altro che la velocità angolare media del pianeta, come se fosse inserito in un’orbita circolare.  In realtà, a volte il pianeta la supera e a volte è più lento, ma al completamento dell’orbita tutto torna al suo posto. Una grandezza facilissima da calcolare, che ci servirà in seguito.

Tracciamo in figura il cerchio di raggio a e di centro C. Notiamo che se il pianeta descrivesse la circonferenza e se il Sole fosse al centro la sua velocità, costante, sarebbe proprio il moto medio.

Noi, invece, tracciamo da R la perpendicolare a CP e l’allunghiamo fino a incontrare la circonferenza in Q. Introduciamo l’angolo E (QCP) e lo chiamiamo anomalia eccentrica.

E è un angolo davvero “simpatico” (ma non solo…). Confrontiamolo con l’anomalia vera f in Fig. 6.

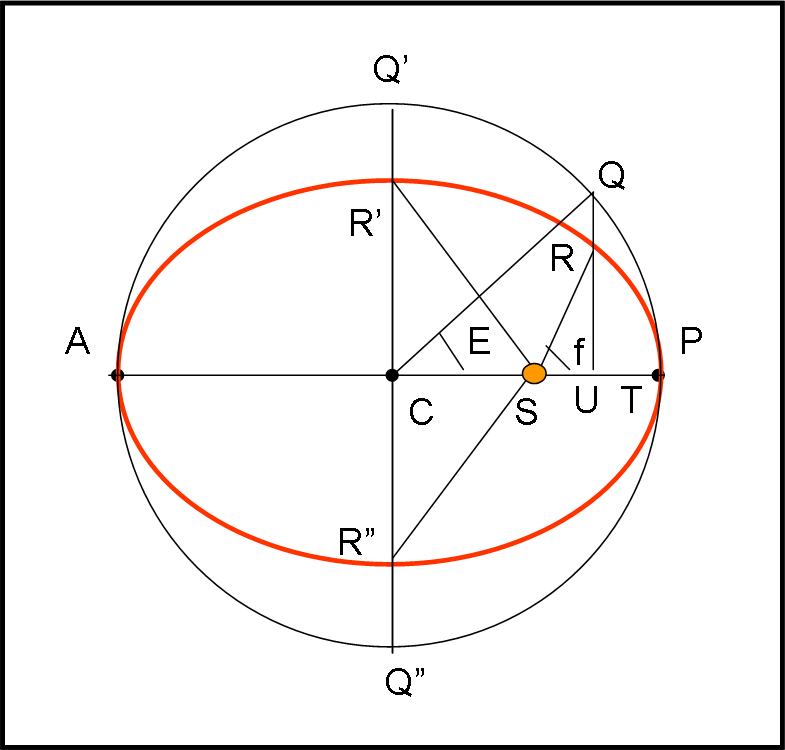
Quando il pianeta è al perielio P, i punti R e Q coincidono ed è E = f = 0.  Quando il punto R si porta in R’, Q arriva in Q’. Sono entrambi sulla verticale passante per C e l’angolo E è uguale a 90°, decisamente più piccolo di f. Tuttavia, essi tornano a essere uguali quando il pianeta raggiunge l’afelio A. Sembra quasi che E abbia accelerato per raggiungere f. Quando R si porta in R”, Q” sta anch’esso sulla verticale tracciata da C, una situazione simile a quella relativa a E = 90°. Ma, adesso E = 270°, mentre f è decisamente più piccolo. E’ lui che adesso deve accelerare per raggiungere, nuovamente, E al perielio P. Una corsa davvero interessante che fa sicuramente pensare che E ed f siano legati assieme da una qualche relazione. D’accordo che E non è un angolo misurabile, ma è già qualcosa. Oltretutto, non ci può scappare una certa analogia con l’anomalia media…

La faccenda si fa interessante. Dedichiamoci al legame tra anomalia vera e anomalia eccentrica. C’è da divertirsi…

Innanzitutto c’è da ricordarsi o da ricavare un’altra proprietà dell’ellisse che a noi va proprio a fagiolo:

QU/RU = a/b           …. (1)

L’ellisse è veramente una figura fantastica… Come si ottiene questa relazione? Qui di seguito riportiamo la dimostrazione e la scriviamo in corsivo. Chi non la conosce la può leggere, gli altri possono saltarla.

Usiamo la Fig. 7, dove abbiamo disegnato due cerchi concentrici di raggio a e b, rispettivamente.

Tracciamo una qualsiasi retta CQ. Il punto B (intersezione di questa retta con la circonferenza più piccola) appartiene alla circonferenza di raggio b e la sua ordinata y = BD è data da:

y_b = BD = b sen E

Il punto Q appartiene, invece, alla circonferenza di raggio a e la sua ascissa CU è data da:

 x_a = CU = a cos E

Bene, senza fare tanti passaggi possiamo dimostrare facilmente che il punto R dell’ellisse ha coordinate

x = a cos E

y = b sen E

Proviamo? Basta elevare a quadrato le due relazioni:

x²/a² = cos²E

y²/b² = sen²E

Sommiamole e si ottiene:

x²/a² + y²/b² = cos²E + sen²E = 1

Ma un’equazione del tipo:

x²/a² + y²/b² = 1

è proprio l’equazione di un ellisse di semiassi a e b.

Il che vuole dire che RU è uguale a BD, dato che entrambi valgono b sen E. Possiamo, allora considerare i triangoli rettangoli CUQ e CDB.

Essi sono, ovviamente, simili e quindi vale la relazione:

QC/BC = QU/BD

Ma… RU è uguale a BD e quindi segue che:

a/b = QU/RU

Proprio quello che volevamo dimostrare.

Torniamo alla Fig. 5, che ci permette di scrivere:

RU = r sen f                                 (r è il raggio vettore)

QU = a sen E

Utilizzando la (1), si ottiene:

a/b = QU/RU = a sen E/r sen f

ossia:

r sen f = b sen E                   …. (2)

Dedichiamoci a SU che vale:

SU = r cos f

Tuttavia SU è anche :

SU = CU – CS

Come sappiamo bene dallo studio dell’ellisse (QUI, capitolo 15)

CS = ae                  (distanza tra centro e fuoco)

CU è invece dato da:

CU = a cos E

Ne segue che:

SU = r cos f  =  a cos E – ae = a(cos E – e)

r cos f  = a(cos E – e)              …. (3)

Eleviamo a quadrato la (2) e la (3) e sommiamole:

r² sen ²f  + r² cos² f  = b² sen²E + a²(cos E – e)²

r² = b² sen²E + a²(cos E – e)²

Sappiamo, però, che (QUI, capitolo 15):

b² = a²(1 – e²)

Sostituendo, si ha:

r² = a²(1 – e²) sen²E + a²(cos E – e)²

Eseguiamo il quadrato di un binomio (QUI, capitolo PN, l'ultimo)

r² = a²sen²E – a²e²sen²E + a²cos²E + a²e² – 2a²e cosE

r² = a²sen²E + a²cos²E + a²e² – a²e²sen²E – 2a²e cosE

Ricordiamo che sen²E + cos²E = 1 e che, analogamente, 1 – sen²E = cos²E

r² = a² + a²e²cos²E – 2a²e cosE

Raccogliendo a², al secondo membro compare il quadrato di un binomio

r² = a²(1 + e²cos²E – 2e cosE) = a²(1 – e cosE)²

E, infine, estraendo la radice quadrata:

r = a(1 – e cosE)        …. (4)

A questo punto dobbiamo introdurre le formule di bisezione (la trigonometria è ricchissima di formule…). Non ve le voglio assolutamente dare dall’alto, ma ricaviamole semplicemente da ciò che già sappiamo. In particolare nel quiz sul barattolo e la formica (QUI), abbiamo introdotto le formule di addizione e sottrazione (la loro dimostrazione è data nell’appendice di quell’articolo). A noi interessa la seconda, ossia:

cos(α + β) = cos α cos β - sen α sen β

La utilizziamo nel caso particolare in cui α = β. Si ottiene:

cos(2α) = cos²α - sen²α          …. (5)

Con questa formuletta si può giocare in due modi molto simpatici:

a) Scriviamo, come ormai sappiamo molto bene:

cos²α = 1 - sen²α

La (5) diventa:

cos(2α) = 1 - sen²α - sen²α = 1 - 2 sen²α

Poniamo adesso, tanto per restare vicini al nostro problema (che è poi quello di Keplero):

2α = f

Si ha:

cos f = 1 - 2 sen²(f/2)

Da cui:

2 sen²(f/2) = 1 – cos f             …. (6)

b) Scriviamo, come sappiamo altrettanto bene:

sen²α = 1 - cos²α

Inseriamola nella (5):

cos(2α) = cos²α – (1 - cos²α) = 2 cos²α – 1

Come prima, poniamo 2α = f e otteniamo:

cos f = 2 cos²(f/2) – 1

Da cui:

2 cos²(f/2) = 1 + cos f              …. (7)

Notiamo quante cose si possono fare partendo dalla semplice relazione fondamentale sin²(α) + cos²(α) = 1. Sembra quasi impossibile… la matematica sa essere fantasiosa e sorprendente come poche altre discipline!

Torniamo a noi con la (6) e la (7). Tanto per gradire moltiplichiamole per r:

2 r sen²(f/2) = r(1 – cos f)

2 r cos²(f/2) = r(1 + cos f)          …. (8)

Dobbiamo cercare di scrivere i secondi membri in funzione dell’anomalia eccentrica E. Andiamo a cercare, nella trattazione precedente, qualche relazione utile allo scopo.

Una è la (3), che dice:

r cos f  = a(cos E – e)

Un’altra è la (4) che dice:

r = a(1 – e cosE)

Riscriviamo le (8) e andiamo a sostituire ciò che dicono la (3) e la (4)

2 r sen²(f/2) = r(1 – cos f) = r – r cos f = a(1 – e cosE) - a(cos E – e)

2 r sen²(f/2) = a - ae cos E – a cosE + ae = a(1 + e) – a cosE (1 + e)

2 r sen²(f/2) = a(1 + e)(1 – cosE)             …. (9)

 

2 r cos²(f/2) = r(1 + cos f) = r + r cos f =  a(1 – e cosE) + a(cos E – e)

2 r cos²(f/2) =  a – ae cosE + a cosE – ae = a(1 – e) + a cosE (1 - e)

2 r cos²(f/2) = a(1 – e)(1 + cosE)             …. (10)

Compattiamo la (9) e la (10), dividendo la prima per la seconda:

sen²(f/2)/cos²(f/2) = ((1 + e)/(1 – e)) (1 – cosE)/(1 + cosE)

tan²(f/2) = ((1 + e)/(1 – e)) (1 – cosE)/(1 + cosE))     …. (11)

Ancora uno sforzo… non mollate proprio adesso!

Ricordiamoci la (6) e la (7), dove al posto di f inseriamo E (le formule valgono per qualsiasi angolo). Otteniamo:

2 sen²(E/2) = 1 – cos E

2 cos²(E/2) = 1 + cos E

Sostituendo, la (11) diventa:

tan²(f/2) = ((1 + e)/(1 – e)) (sen²(E/2)/cos²(E/2))

tan²(f/2) = ((1 + e)/(1 – e)) tan²(E/2)

Estraendo la radice quadrata, otteniamo, finalmente:

tan (f/2) = ((1 + e)/(1 – e))^1/2 tan (E/2)            …. (12)

La (12) è veramente importante: permette di ricavare l’anomalia vera in funzione dell’anomalia eccentrica, conoscendo, ovviamente, l’eccentricità.

Questo è solo il primo passo del problema di Keplero, dato che l’anomalia eccentrica non può misurarsi. Tuttavia, abbiamo già intuito che essa potrebbe essere collegata all’anomalia media e quest’ultima è di immediata determinazione, dipendendo solo dal periodo orbitale.

Il secondo passo è, allora, quello di legare anomalia eccentrica  e anomalia media. Il genio di Keplero c’è riuscito, anche se ciò che trova non è di facile soluzione e prende proprio il nome di equazione di Keplero.

QUI trovate tutti gli articoli su “Gli elementi orbitali e i loro compari”

Chi ha voglia e curiosità di fare due chiacchiere con Keplero in persona (e non solo lui), può trovarlo QUI