Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Adesso che abbiamo a disposizione il lemma di Zorn, siamo in grado di dimostrare  Il  teorema di Zermelo (o del buon ordinamento)

Ogni insieme X è ben ordinabile, ovvero è possibile trovare per X un ordinamento che sia totale, e per cui ogni sottoinsieme Y di X abbia minimo.

Per dare un buon ordine, è necessario dare un insieme e un ordine fra i suoi elementi. Se B è un sottoinsieme di X, indichiamo con  la coppia () un certo buon ordine. Consideriamo adesso l'insieme di tutti questi buon ordini, e chiamiamolo ; dunque

; in pratica costruiamo un nuovo insieme,  , i cui elementi sono dei buoni ordini. Ci vuole un certo sforzo di astrazione  per comprendere ciò. L'insieme  non è vuoto: infatti se consideriamo dei sottoinsiemi B finiti di X, essi sono ben ordinabili (1)(vedi nota in fondo alla pagina).

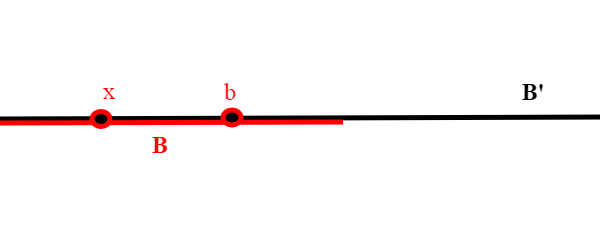
Stabiliamo adesso su  un ordine in tal modo; diremo che  se B è un segmento iniziale di B';questo equivale a richiedere tre cose:

i)

ii)la relazione  ristretta a B coincida con 

iii)se x  b con b appartenente a B, allora anche x appartiene a B (non basta essere sottoinsiemi per essere segmenti iniziali, ci vuole una condizione in più).

La relazione  è una relazione d'ordine (parziale) su .

Semplifichiamo un po' le notazioni; indichiamo con   la coppia (A,),  la coppia (B,),  la coppia (C,)

Dobbiamo verificare le tre proprietà

1) simmetrica

sia qualsiasi; chiaramente A è segmento iniziale (non proprio) di se stesso, quindi

2) antiriflessiva

dobbiamo dimostrare che se   allora =; ma se A è sottoinsieme di B e B sottoinsieme di A  allora A=B.

3) transitiva

dobbiamo provare che da  ,   segue  

i)

ii)la relazione  ristretta a B coincide con ; anche la relazione   ristretta su A coincide con ; ne segue che  ristretta su A coincide con .

iii) se a appartiene ad A e x<A, anche x appartiene ad A (è segmento iniziale di B)

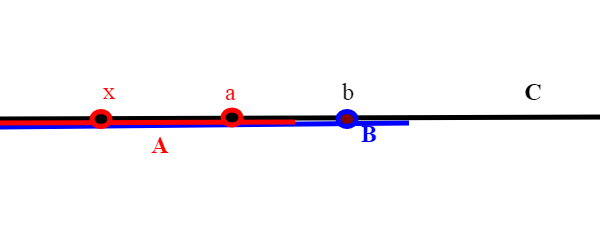Consideriamo ora una  qualsiasi catena C  di elementi di  :

; sappiamo da un articolo precedente che l'unione di un insieme (collezione,famiglia) di buoni ordini che sono uno un segmento iniziale dell'altro è ancora un buon ordine , quindi un elemento di , e inoltre tale elemento è un maggiorante per la catena; siamo nelle ipotesi del lemma di Zorn(per ogni catena esiste un maggiorante) quindi esiste un elemento massimale . Resta da dimostrare che M=X.

Se fosse  , possiamo prendere un elemento  X\M; Notiamo che  è un elemento per così dire "libero", in quanto non è in relazione con alcun elemento di M. Consideriamo l'insieme (sottoinsieme di X) D=M  U {}; definiamo un buon ordine in tal modo, (M  U {},) dove poniamo    maggiore di tutti gli elementi di M. In pratica, su M abbiamo l'ordine  qualsiasi siamo x,y in M, mentre al più può succedere che uno dei due (o entrambi) siano uguali a .  Ma allora (D,) sarebbe un buon ordine, e M segmento iniziale di D,generato da , quindi ; ma allora   non sarebbe più massimale.

Quindi M=X; ma allora , quindi X è totalmente ordinato.

Conseguenza immediata del teorema di Zermelo è la confrontabilità dei numeri cardinali. 

Riprendiamo un teorema sugli isomorfismi (dimostrato qui) :

Dati due buoni ordini A e B uno dei due è isomorfo ad un segmento iniziale dell'altro (non necessariamente proprio).

Se consideriamo due  insiemi (infiniti) A e B qualsiasi, possiamo applicare ad essi il teorema di Zermelo e  ben ordinarli. Siamo adesso nelle ipotesi del teorema sugli isomorfismi; l'isomorfismo in fin dei conti è una applicazione biunivoca, che in più , nel caso di insiemi ordinati, conserva l'ordine. Il segmento iniziale di un insieme  è anche un sottoinsieme; dire che esiste una applicazione biunivoca di A in un segmento iniziale di B, vuol anche dire che esiste una applicazione biunivoca di A in un sottoinsieme di B (e questo nel caso dei cardinali significa che |A| <=|B|). Il fatto che il segmento iniziale possa non essere proprio si traduce con la possibilità che sia |A|=|B|.

La tricotomia dei numeri cardinali si esprime anche cosi:

Dati due insiemi A,B esistono tre possibilità:

1. |A|<|B|
2. |A|>|B|
3. !A|=|B|

nota (1)

Sebbene non sia mai sottolineato , il fatto che BO non sia vuoto perchè i sottoinsiemi B finiti di X sono ben ordinabili è un punto fondamentale della dimostrazione. Finchè siamo nel finito non ci sono problemi; possiamo dare un ordine in un insieme come vogliamo, mediante una relazione fra elementi  di B X B; per trovare il minimo di un insieme finito , che senz'altro esiste,possiamo applicare l'algoritmo che meglio ci aggrada.