Questo articolo è esattamente uguale a quello precedente (terza parte) ed è, quindi, la diretta continuazione del secondo  e del primo . Ho inserito all’interno le risposte alle domande che erano state fatte (tre). Per cui, posso tranquillamente eliminare quello che avevo identificato come terza parte, che viene sostituito da questo.

La parte più difficile del problema viene spiegata in questo articolo (il terzo di una serie di cui i primi due trovate QUI e QUI). Tuttavia, l’appetito vien mangiando e la trattazione si conclude con ben tre ulteriori QUIZ, di più facile soluzione, che vengono date direttamente (magari prima di guardarle pensateci un po' sopra). Non arrabbiatevi, ma sono convinto che la ricerca di soluzioni e il trucco matematico che trovate all’interno di questo articolo (ammetto che è un po’ troppo “arduo” da immaginare) non possono che stimolare sempre di più una mente vogliosa di apprendere e di agire. Un bravo particolare, comunque, a Leandro che ha impostato correttamente la funzione e stabilito altrettanto correttamente l’apparente impossibilità di proseguire.

Iniziamo con lo scrivere la funzione che contraddistingue il percorso più generale della formica.

La Fig. 6 (praticamente la vecchia Fig. 5) ci porta velocemente alla funzione s dell’angolo φ. Essa si divide in due tronconi, la prima parte descrive il percorso da A a P  la seconda il percorso da P a B. P, ovviamente, appartiene sia alla circonferenza che al cilindro srotolato.

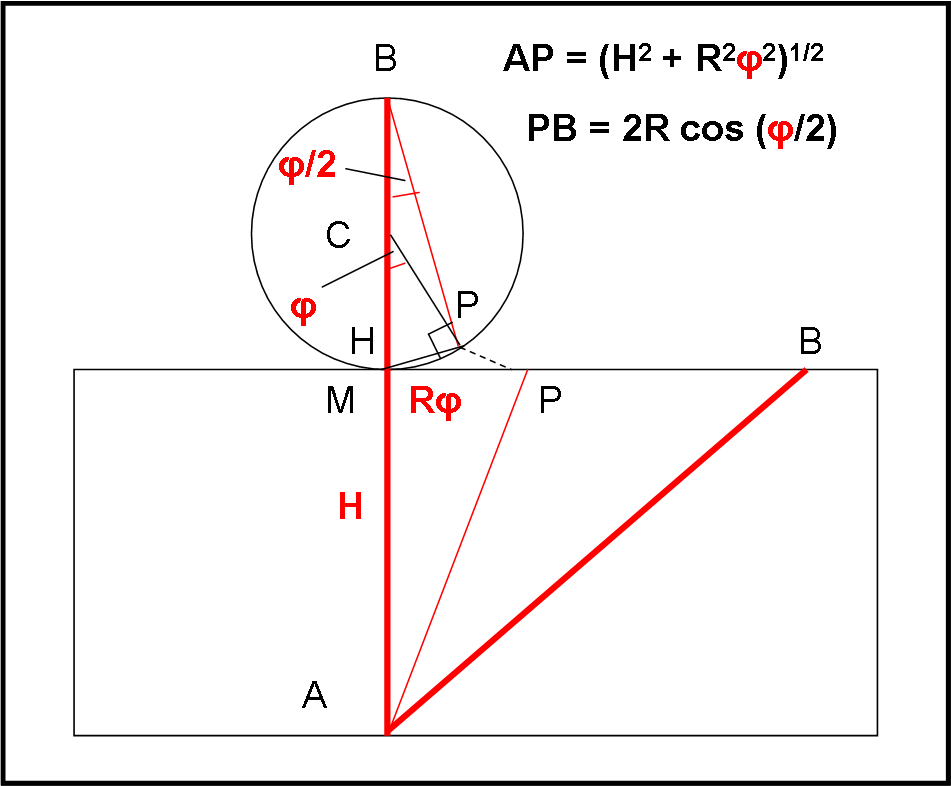
Ricordando che il segmento MP (sul cilindro) è uguale all’arco di circonferenza MP (sul cerchio) e che quest’ultimo vale Rφ, dal teorema di Pitagora applicato al triangolo AMP sul cilindro srotolato, abbiamo:

AP = (H² + R²φ²)^1/2

Portiamoci adesso sul cerchio. Sappiamo che l’angolo in HBP è la metà dell’angolo al centro HOP, dato che insistono sullo stesso arco MP (dimostrazione nell’Appendice). Inoltre l’angolo BPH deve essere retto dato che insiste su un arco uguale a metà della circonferenza. Ne consegue che il triangolo BPH è rettangolo in P. Si ha subito che:

PB = BH cos(PBH)

Ossia:

PB = 2R cos(φ/2)

Il percorso totale s(φ) è quindi dato dalla somma dei due segmenti e, quindi, da:

s = (H² + R²φ²)^1/2 + 2R cos(φ/2)         …. (1)

Notiamo che l’unica variabile è proprio φ, dato che H e R sono stati fissati e quindi sono termini noti.

Risulta chiaro che non sarebbe assolutamente giusto confrontare soltanto gli estremi di questa funzione (φ = 0° e φ = 180°) per decidere quale sia il percorso minimo. Può darsi che uno dei due lo sia veramente, ma lo possiamo dire solo dopo aver studiato la funzione nell’intervallo 0° < φ < 180°.

Come facciamo a verificare se la funzione presenta dei minimi (o massimi) al suo interno? Beh… lo sappiamo molto bene dallo studio delle funzioni (QUI). Basta eseguire la derivata prima e studiare i punti in cui si annulla.

Non ci resta, allora, che derivare la (1) rispetto a φ.

ds/dφ = R²φ/(H² + R²φ²)^1/2 – R sen(φ/2)            (le derivate potete calcolarle voi…)

e poi uguagliare a zero.

R²φ/(H² + R²φ²)^1/2 – R sen(φ/2) = 0

O ancora:

R²φ/(H² + R²φ²)^1/2 = R sen(φ/2)

sen(φ/2) = Rφ/(H² + R²φ²)^1/2     …. (2)

In parole povere, si ha un massimo o un minimo (o un flesso orizzontale, teoricamente…), quando vale l’uguaglianza (2). Bene… potete provare quanto volete, ma non troverete modo di risolvere l’equazione (2), ossia non c’è modo di esprimere φ in funzione di H e R attraverso funzioni elementari.

Dobbiamo abbandonare l’impresa e andare a tentativi, punto a punto? Direi proprio di no. Possiamo ancora fare qualcosa di risolutivo senza tralasciare il formalismo matematico. Basta ricordare ancora lo studio delle funzioni.

Sappiamo che per decidere se un punto in cui si annulla la derivata prima è un punto di massimo o di minimo, si può calcolare la derivata seconda e vedere il suo segno. Se essa è minore di zero abbiamo un punto di massimo, se è maggiore di zero, abbiamo un punto di minimo.

Per quello che interessa a noi, è sufficiente verificare una di queste situazioni. Se trovassimo una derivata seconda minore di zero, saremmo certi che non esiste alcun minimo all’interno dell’intervallo in cui si studia la funzione e, quindi, sapremmo che il minimo cade proprio in uno dei due estremi. La risposta più semplice data precedentemente sarebbe giusta. Se, invece, trovassimo una derivata seconda positiva, dovremmo ammettere che siamo stati troppo frettolosi. In ogni modo, per correttezza, la prova deve essere fatta.

Cominciamo col calcolare la derivata seconda della (1):

d²s/dφ² = R²H²/((H² + R²φ²)^1/2)³ – R cos(φ/2)/2   …. (3) (continuate a fare esercizio con le derivate…)

Sì, sì, molto bella… anche se è addirittura più complicata della prima. Inoltre, sarà anche bello aver calcolato la derivata seconda, ma per sapere il suo segno è necessario calcolarla nel punto in cui si annulla la derivata prima. E questo è proprio quello che vorremmo sapere. Sembra proprio un serpente che si morde la cosa. Però, però, potremmo usare un bel trucco!

Qualsiasi sia il punto che annulla la derivata prima, esso deve soddisfare la (2). Perché, allora, non scriviamo la (2) in modo tale da poterla inserire nella (3)? Facendo questo avremmo una (3) che si riferisce proprio al punto che soddisfa la (2). Ovviamente, non c’è speranza di ricavare valori numerici, ma c’è la possibilità di valutare in qualche modo il segno della (3), in cui è stato sostituito il valore che soddisfa la (2). Il punto misterioso non si vede, ma c’è!

Cerchiamo di trasformare i “pezzi” della (3) dove compare H, utilizzando la (2). in modo che questo parametro sparisca a vantaggio di φ . Chissà mai…

Mettiamo le mani nella (2), scrivendola in altro modo:

(H² + R²φ²)^1/2 = Rφ/sen(φ/2)          …. (4)

Un pezzo è stato ricavato…

Adesso, eleviamo a quadrato:

H² + R²φ² = R²φ²/sen²(φ/2)

E ricaviamo H²

H² = R²φ²/sen²(φ/2) - R²φ²

H² = R²φ²(1/sen²(φ/2) – 1)

H² = R²φ²(sen²(φ/2) + cos²(φ/2) - sen²(φ/2))/sen²(φ/2)     (ricordando che sen²(φ/2) + cos²(φ/2) = 1)

H² = R²φ²cos²(φ/2)/sen²(φ/2)       …. (5)

E anche il secondo pezzo è stato trovato…

Prendiamo la (4) e la (5) e andiamo a sostituirli nella (3). Stiamo proprio inserendo il valore che soddisfa la (2), nella (3). Si ottiene:

d²s/dφ² = R² (R²φ² cos²(φ/2)/sen²(φ/2))/(Rφ/sen(φ/2))³ – R cos(φ/2)/2

Praticamente è come se avessimo la derivata seconda calcolata nel punto che annulla la derivata prima. Basta, adesso, semplificarla, compattarla, studiarne il segno e… lavorare con molta calma e attenzione.

d²s/dφ² = R(cos²(φ/2) sen(φ/2))/φ – R cos(φ/2)/2

d²s/dφ² = (R/2φ) 2cos²(φ/2) sen(φ/2) – φ cos(φ/2))     

d²s/dφ² = (R/2φ) cos(φ/2) (2 cos(φ/2) sen(φ/2) – φ )         …. (6)

A questo punto, bisogna conoscere le formule trigonometriche dell’addizione e sottrazione, ossia:

cos(α - β) = cos α cos β + sen α sen β

cos(α + β) = cos α cos β - sen α sen β

sen(α - β) = sen α cos β - cos α sen β

sen(α + β) = sen α cos β + cos α sen β

Le dimostriamo nell’Appendice e, per adesso, le prendiamo per buone. In particolare usiamo la quarta, ossia:

sen(α + β) = sen α cos β + cos α sen β             …. (7)

La usiamo, però, per due angoli particolari, ossia per α = β = φ/2. La (7) diventa:

sen(2φ/2) = sen(φ/2) cos(φ/2) + cos(φ/2) sen(φ/2) = 2 sen(φ/2) cos(φ/2)

sen(φ) = 2 sen(φ/2) cos(φ/2)           …. (8)

Ma, nel secondo membro della (6) abbiamo proprio il secondo membro della (8). Possiamo sostituirlo e la (6) diventa:

d²s/dφ² = (R/2φ) cos(φ/2) (sen(φ) – φ )

Possiamo finalmente analizzare il segno di questa espressione per  0° < φ < 180°, ossia in tutto l’intervallo della funzione, tranne che nei due punti estremi che già conosciamo.

La quantità (R/2φ) cos(φ/2) è sempre POSITIVA, dato che il coseno è sempre positivo e varia tra 0 e 1. Il segno della derivata seconda dipende, perciò, solo e soltanto dall’espressione:

sen(φ) – φ

Tuttavia, sappiamo benissimo che il seno di un angolo è sempre minore dell’angolo espresso in radianti, nell’intervallo 0 < φ < π. Basterebbe mettere in grafico le funzioni s = sen(φ)  e s = φ per confermarlo (Fig. 7)

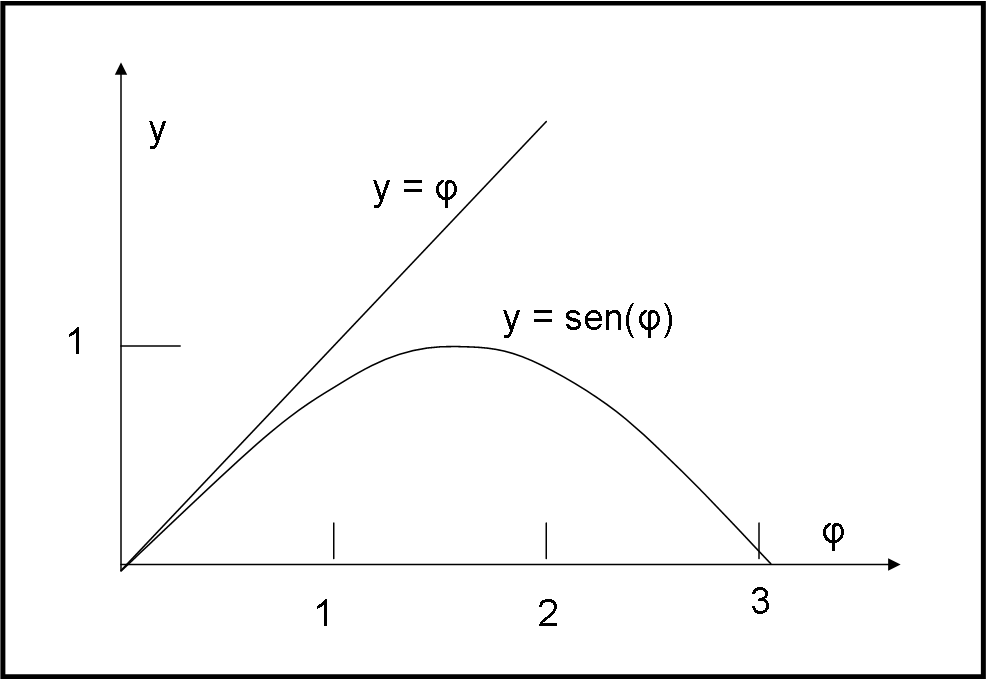
La conclusione è che la derivata seconda nel punto in cui si annulla la derivata prima NON può essere un minimo, dato che la derivata seconda sarebbe negativa.

Ne segue che il percorso minimo, per qualsiasi valore di H e di R, deve trovarsi in uno dei suoi estremi, ossia in uno dei casi trattati all’inizio dell’articolo.

Le soluzioni iniziali erano quindi quelle esatte, ma solo per un caso fortunato. In realtà, si era arrivati alla conclusione senza tener conto delle vie alternative e senza valutare se potessero essere le più corte. In altre parole ci siamo limitati a guardare i due estremi di una funzione, senza curarci di cosa faceva tra uno e l'altro. Questo esempio, non certo banale, vuole solo mettere in guardia di fronte a soluzioni apparentemente semplici e rapide. Vale sempre la pena di ragionarci un po’ sopra. Di questi tempi, dominati dalla fretta e da pressapochismo, questo articolo può essere veramente utile.

Ma… ma… siamo proprio sicuri di aver provato tutte le strade? In realtà, no! Vi è ancora una possibilità attraverso percorsi come quello indicato nella Fig. 8.  La parte a tratteggio è un percorso fatto sulla base inferiore circolare (ossia è una corda della base). No, non arrabbiatevi. Non è difficile dimostrare che questa via è più lunga di quella precedente, anche solo graficamente. Provate, comunque, a dimostrarlo…

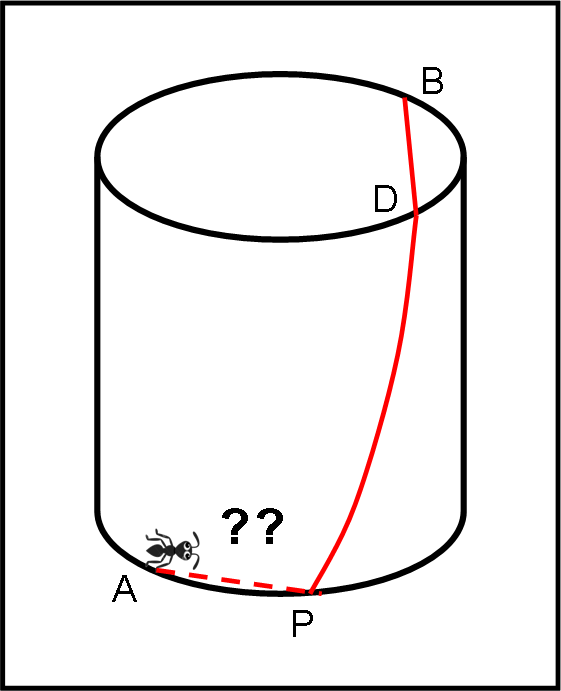
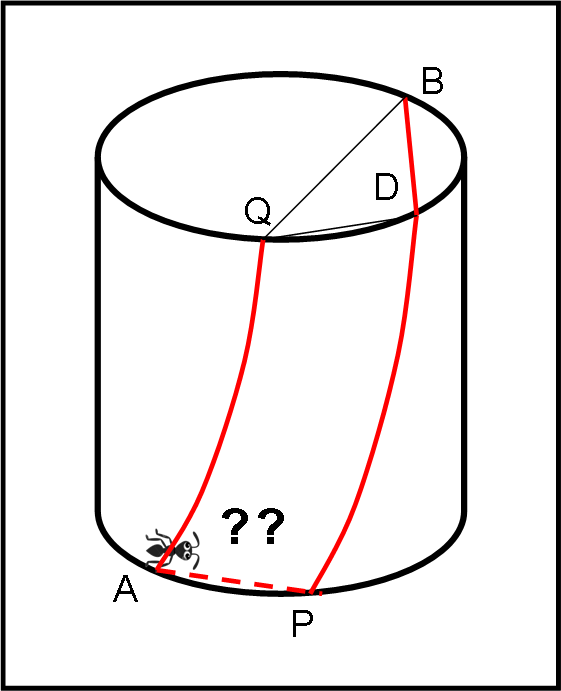
La soluzione per questo ulteriore percorso è decisamente facile. Basta considerare (per la geometria del cilindro) che il percorso è esattamente uguale a quello indicato come AQDB in Fig. 8bis (AQ = PD). Tuttavia, il tratto QDB, qualsiasi sia il percorso da Q a D (o circolare o rettilineo) è obbligatoriamente minore della via diretta QB, che è già stata trattata. Per cui, il nuovo percorso è decisamente più lungo dei precedenti già trattati esaurientemente.

Appendice (per i meno esperti)

Più che un appendice, in questa prima fase, è una coppia di quiz... Perdonatemi, ma le soluzioni sono proprio alla portata di tutti coloro che conoscono le regole della più semplice geometria e le basi classiche della trigonometria.

a) L’angolo al centro di una circonferenza, che insiste in un arco qualsiasi, è il doppio di quello alla circonferenza relativo allo stesso arco. Meglio di tante parole vale la Fig. 9.

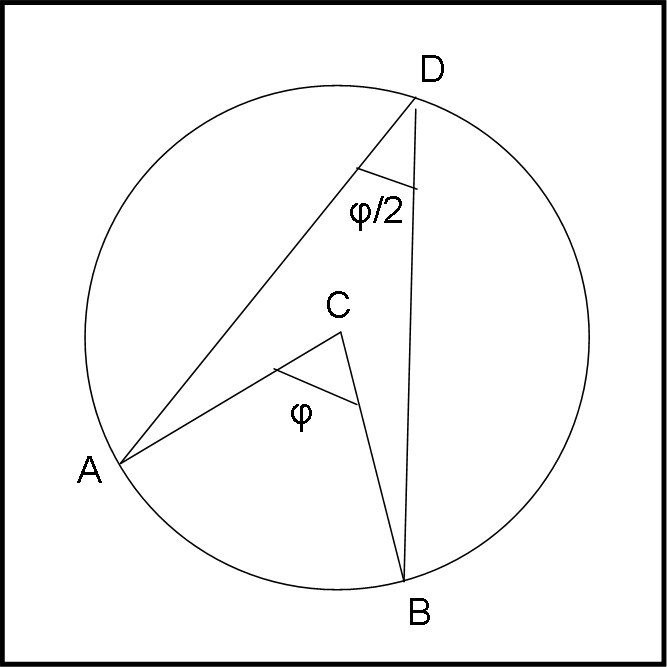
Cercate di dimostrarlo da soli… basta trovare i triangoli giusti...

Lo facciamo in Fig. 9bis

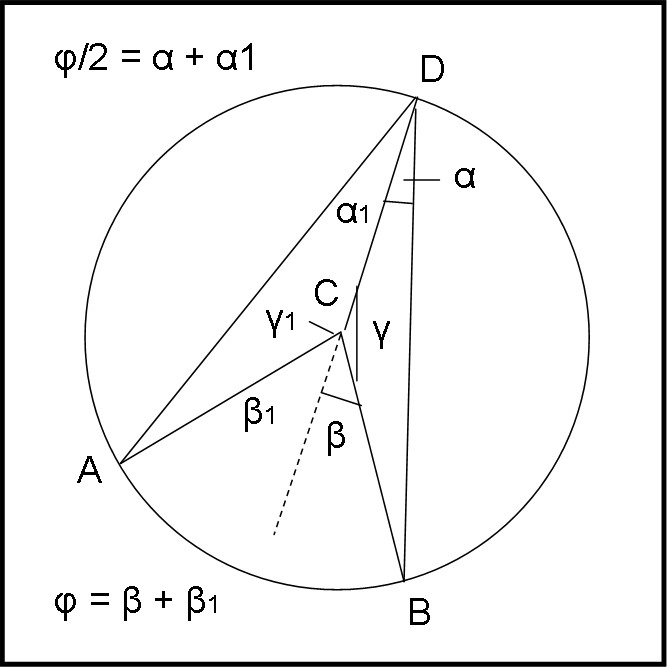
Tracciamo la congiungente DC, prolungandola oltre C. Il triangolo DCB è isoscele, dato che CD = CB = raggio. L'angolo in D e l'angolo in B devono essere uguali ad α.

L’angolo γ è uguale, perciò, a 180 - 2α. Ne segue che β deve essere uguale a 2α.  Considerando il triangolo ACD otteniamo un risultato analogo, ossia β₁ = 2α₁.

Ne segue che, l’angolo al centro, ossia φ, vale:

φ = β + β₁ = 2α + 2α₁ = 2(α + α₁)

Ma l’angolo alla circonferenza (quello in D) è dato da:

α + α₁ = φ/2

Come volevasi dimostrare.

b) Valgono le seguenti relazioni additive e sottrattive per il seno e il coseno di due angoli:

cos(α - β) = cos α cos β + sen α sen β

cos(α + β) = cos α cos β - sen α sen β

sen(α + β) = sen α cos β + cos α sen β

sen(α - β) = sen α cos β - cos α sen β

Partiamo dalla prima e tutte le altre saranno un’ovvia conseguenza.

Tanto che ci siamo, provate a dimostrare anche queste relazioni… bastano un paio di segmenti e le proprietà del seno e del coseno...

Iniziamo a dimostrare la prima relazione:

cos(α - β) = cos α cos β + sen α sen β

Per far ciò disegniamo la Fig. 10. I vari angoli sono identificati in figura e a ogni punto sono associate le relative coordinate.

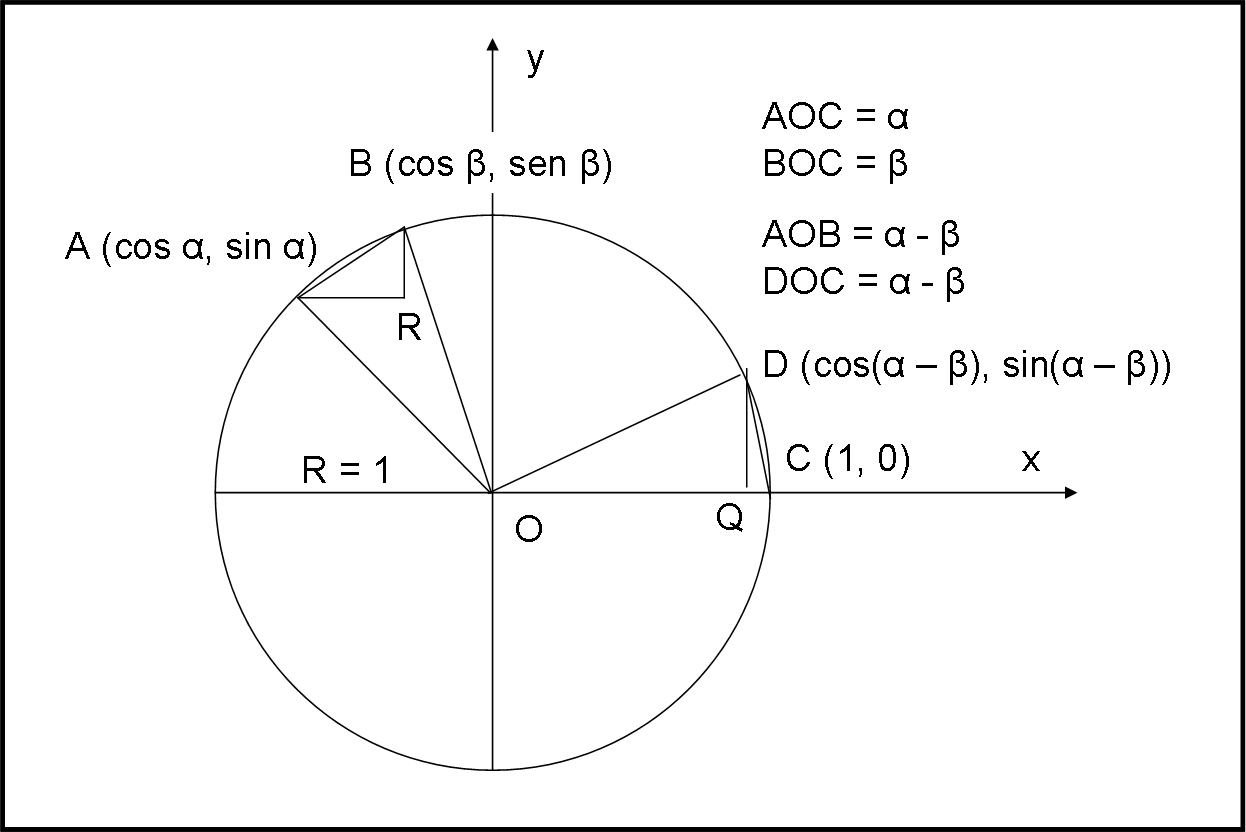
Costruiamo l’angolo DOQ = AOB nel primo quadrante. Gli archi DC e AB devono essere uguali e altrettanto devono esserle le corde AB e DC. Ricordando il teorema di Pitagora (o la definizione di distanza tra due punti, che è la stessa cosa…), possiamo scrivere:

AB = (AR² + BR²)^1/2 = ((cosα – cosβ)² + (senα – senβ)²)^1/2

DC = (DQ² + CQ²)^1/2 = ((cos(α – β) - 1)² + (sen(α – β) – 0)²)^1/2

Uguagliamo le due relazioni:

((cosα – cosβ)² + (sinα – sin β)²)^1/2 = ((cos(α – β) - 1)² + sen²(α – β))^1/2

(cosα – cosβ)² + (sinα – sinβ)² = (cos(α – β) - 1)² + sen²(α – β)

Eseguiamo tutti i quadrati (si fa in fretta!):

cos²α + cos²β - 2cosα cosβ + sin²α + sin²β - 2 senα senβ = cos₂(α - β) + 1 - 2cos(α - β) + sen²(α - β)

semplifichiamo, ricordando che sin²φ + cos²φ = 1:

1 + 1 – 2 cosα cosβ - 2 senα senβ = 1 + 1 – 2 cos(α – β)

Semplificando ancora e cambiando di segno:

2 cosα cosβ + 2 senα senβ = 2 cos(α – β)

E, infine:

cos(α – β) = cosα cosβ + senα senβ           …. (9)

La prima relazione è stata dimostrata.

Passiamo alla seconda…

cos(α + β) = cos α cos β - sen α sen β

Ci sbrighiamo in fretta, riducendoci a quella precedente. Consideriamo, nella (9), come angolo β l’angolo – β. La relazione diventa:

cos(α - (- β)) = cos α cos(- β) + sen α sen(- β)

Essa diventa, ricordando che cos(- β) = cos(β) e che sen(- β) = - sen(β) (QUI):

cos(α + β) = cos α cos β - sen α sen β        …. (10)

che è proprio la seconda.

Passiamo alla terza:

sen(α + β) = sen α cos β + cos α sen β

Ricordiamo subito una proprietà degli angoli complementari:

sen(α + β) = cos (90 – (α + β)) = cos((90 – α) - β))

Siamo ricaduti nella formula (9) e, quindi, possiamo scrivere:

sen(α + β) =  cos(90 – α) cosβ + sen(90 – α) senβ

Ossia:

sen(α + β) = sen α cos β + cos α sen β           …. (11)

come volevasi dimostrare.

Passiamo, infine, alla quarta:

sen(α - β) = sen α cos β - cos α sen β

La procedura è veramente banale. Ponendo – β al posto di β, nella (11), abbiamo:

sen(α + (- β)) = sen α cos(- β) + cos α sen(- β)

sen(α - β) = sen α cos β - cos α sen β      …. (12)

come volevasi dimostrare.

Sarà stato un articolo anche un po’ lungo e noioso(?), ma abbiamo imparato molte cose.

Non possiamo che finire augurando alla nostra formica di cadere all’interno del barattolo, pieno di zucchero, come dice Daniela!