Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Le relazioni e le classi di equivalenza aprono un altro capitolo estremamente importante della teoria degli insiemi. Tramite le classi di equivalenza è stato possibile formalizzare correttamente le definizioni di numero intero, razionale ed altro ancora.  In poche parole costruire una base solida della matematica.

Prima di parlare di relazioni di equivalenza,  devo introdurre un'altro concetto che riguarda gli insiemi:

La partizione di un insieme.

Una partizione di un insieme X è una divisione di X in sottoinsiemi, dette classi della partizione, che "coprono" X senza sovrapporsi. Tali sottoinsiemi sono non vuoti, ovvero hanno almeno un elemento.

Dall'immagine è chiaro di cosa stiamo parlando: Abbiamo dei sottoinsiemi (non vuoti) di un insieme A che sono disgiunti (comunque ne prendiamo due, non hanno elementi in comune) e tali che la loro unione dia tutto X.

Facciamo comunque un esempio : Sia A ={0,1,23,4,5,6,7,8,9,10} ;

I tre sottoinsiemi:

B={0,1,2,3,4}; C={5,6,7,8}; D={9,10};  costituiscono una partizione di A

Infatti non sono vuoti, non hanno elementi in comune e la loro unione dà tutto A.

Relazioni tra gli elementi di un insieme.

Consideriamo un insieme qualsiasi; potremmo prendere per esempio gli abitanti di una certa città. Questi sono gli elementi di un certo  insieme. Ma cosa può legarli fra loro? Una relazione. Prendiamo due elementi a e b. Per esempio:

"a è sposato con b "è una relazione. "a è figlio di b " rappresenta un' altra relazione fra due elementi dell'insieme.

Non farò una trattazione formale delle relazioni, che esula dagli obiettivi che vogliamo raggiungere. Tratteremo inoltre solo relazioni definite fra elementi di uno stesso insieme A. Possiamo anche pensare di rappresentare una relazione tramite una tabella:

A	a1	a2	a3	a4
a1				*
a2	*
a3		*
a4			*

 

Infatti una relazione altro non è che un sottoinsieme di A x A (insieme prodotto di A), ovvero formato dalle coppie che stanno appunto in relazione fra loro.

Le proprietà delle Relazioni di equivalenza.

Un tipo particolare di relazione fra due elementi di uno stesso insieme è quella di equivalenza, che ha delle particolari caratteristiche ( o proprietà).

(Se a è in relazione di equivalenza con b scriveremo a b)

Una relazione si dice di equivalenza se sono valide  le seguenti proprietà:

Proprietà riflessiva

a  a (ovvero a è in relazione con se stesso)

Proprietà simmetrica

se a b allora b  a (se a è in relazione con b, allora  anche b è in relazione con a)

Proprietà transitiva

se a b e b c allora a  c (se a è in relazione con b, b è in relazione con c, allora a è in relazione con c)

Notiamo che per il fatto che è riflessiva, una relazione di equivalenza è definita su tutto A; infatti c'è sempre almeno un elemento che è in relazione con x, ed è x stesso.

Esempi.

"a è figlio di b " non è una relazione di equivalenza; non vale infatti la proprietà simmetrica (se a è figlio di b , b non può essere figlio di a) e nemmeno quella riflessiva (a non può essere figlio) di se stesso.

Invece se   A è l'insieme delle rette nel piano, il parallelismo fra rette è una relazione di equivalenza.

Infatti;

Proprietà riflessiva

una retta è parallela a se stessa.

Proprietà simmetrica

se a è parallela a b, chiaramente  b è parallela ad a.

Proprietà transitiva

se a è parallela a b, e b è parallela a c, allora a è parallela a c.

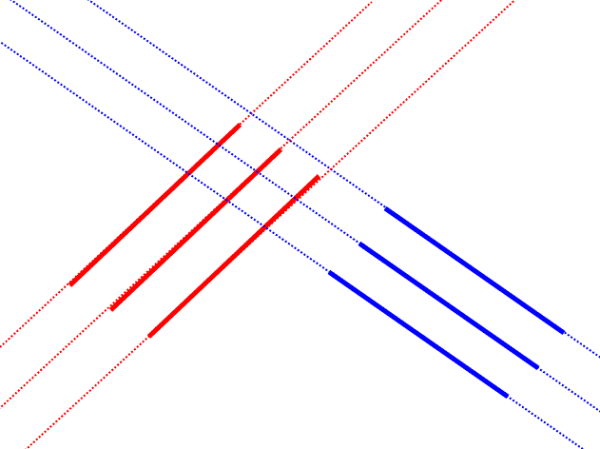
Consideriamo l'insieme delle automobili di una certa città. La relazione "hanno lo stesso colore" è una relazione di equivalenza.

Proprietà riflessiva:Infatti a ha lo stesso colore di a

Proprietà simmetrica:Se a e b hanno lo stesso colore, lo stesso dicasi per b e a

Proprietà transitiva:se a e b hanno lo stesso colore, e b e c hanno lo stesso colore, allora anche a e c hanno lo stesso colore.

Classi di equivalenza.

Un sottoinsieme di A che contiene tutti e soli gli elementi equivalenti a un qualche elemento x di A prende il nome di classe di equivalenza di x per la relazione . Si indica una classe di equivalenza con [x]. In una classe di equivalenza tutti gli elementi in essa contenuti sono tra loro equivalenti.

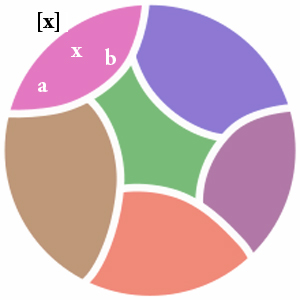
Se torniamo all'esempio delle macchine dello stesso colore, e supponiamo che x sia una macchina di colore fucsia , allora l'insieme delle macchine di colore fucsia è costituito da {x,a,b} e lo indichiamo con [x]. La scelta del rappresentante, in questo caso x, non conta; se prendiamo a o b, la classe (colore) non cambia.

Volevo dimostrare formalmente quanto asserito sopra:

Se x 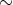 y allora [x]=[y]

Scegliamo un elemento , allora  zx. Ma xy  ma allora per la proprietà transitiva zy, quindi  , quindi  (tutti gli elementi di [x] appartengono a [y].

Allo stesso modo prendiamo un , allora wy; per la proprietà simmetrica  yx e per la transitiva wx dunque    quindi   . Pertanto [x]=[y]

Insieme quoziente di una relazione di equivalenza.

L'insieme delle classi di equivalenza su A si chiama insieme quoziente di A per la relazione , e viene talvolta indicato con l'espressione A / . Si dimostra che esso rappresenta una partizione di A (per non appesantire il discorso ho messo la dimostrazione in appendice). Il nome (quoziente) deriva dal fatto che agendo sulle classi dividiamo l'insieme.

Sempre nel caso delle macchine, l'insieme quoziente non è altro che l'insieme di tutti i colori delle macchine di una certa città.

Nel caso di parallelismo fra rette, la classe non è che la direzione della retta nel piano. L'insieme quoziente è invece l'insieme di tutte le direzioni possibili.

Nel prossimo articolo useremo il concetto di classe di equivalenza per  definire la cardinalità dell'insieme senza contare i suoi elementi.

Appendice

Questa appendice è un po' formale; chi vuole una dimostrazione rigorosa del fatto che l'insieme quoziente è una partizione di A la legga pure, ma non è necessaria per comprendere i prossimi argomenti.

L'insieme quoziente è una partizione di A.

Riscriviamo la definizione di classe di equivalenza in modo un po' più formale.

[x]={  tali che y x  } ricordiamo che questi sono sottoinsiemi di A.

Ricordiamo anche che abbiamo dimostrato che: Se x  y allora [x]=[y]

Dobbiamo dimostrare tre cose:

1 la classe [x] non è mai vuota

Infatti , dato un x appartenente ad A, per la proprietà simmetrica x  x. quindi [x] contiene almeno un elemento.

2 Se [x] , [y] sono le classi di x,y , la loro intersezione è vuota, oppure coincidono.

Supponiamo che l'intersezione fra [x] e [y] dia l'elemento z, allora z x (perché (z appartiene a [x]), x z  (per la proprietà simmetrica) z y (perché z appartiene anche a [y] per la transitiva abbiamo che x  y  . Ma abbiamo dimostrato sopra che   Se x  y allora [x]=[y] , quindi coincidono.

3)L'unione di tutte le classi dà l'insieme A

l'unione di tutte le classi è contenuta in :  (sono sottoinsiemi di A)

Non è possibile che  ovvero : se l'unione fosse contenuta propriamente in A,  allora esisterebbe un x appartenente ad A tale che x non è in relazione con nessun y  appartenente ad A, ma sappiamo che x  x per la proprietà riflessiva.