Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

In questo articolo ci proponiamo di dare la definizione di numero cardinale usando il concetto di classe di equivalenza visto nell'articolo precedente. Questo modo di definire i concetti astratti come classi di equivalenza  risale a Friedric Ludwig Gottlob Frege  matematico, logico e filosofo tedesco, padre della logica matematica moderna ed è molto usato  nella teoria degli insiemi. Potrebbe servire leggere prima questo articolo Corrispondenze e funzioni.

Pensiamo  agli insiemi che possono essere messi in corrispondenza biunivoca fra di loro. Questa è una relazione di equivalenza.

 

Proprietà riflessiva

Chiaramente A può essere messo in corrispondenza biunivoca con se stesso.

(mando ogni elemento a  di A in a ( a--->a)

Proprietà simmetrica

Se A è in corrispondenza biunivoca con B, allora B è in corrispondenza biunivoca con A.

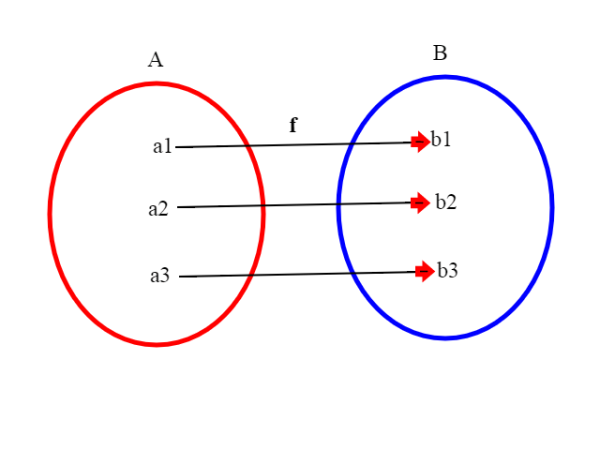
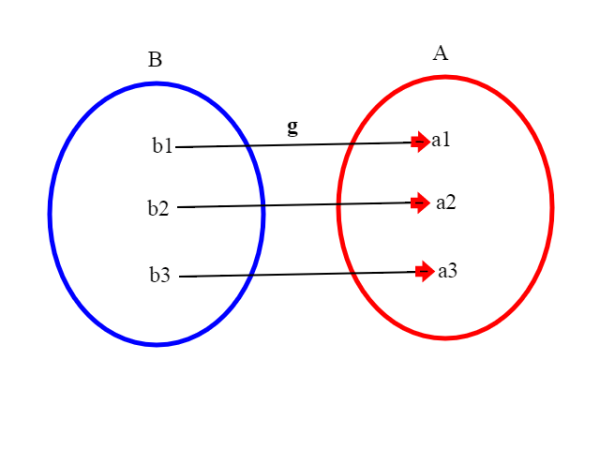
Se  A è in corrispondenza biunivoca con B, la funzione f che va da A a B copre tutto B e manda elementi  distinti in elementi distinti; costruiamo una g che invece va da B in A; dato un b appartenente a B sappiamo che b=f(a) (notiamo che questo a è unico, perchè f è iniettiva) , quindi poniamo g(b)=a. Il fatto poi che a sia unico ci assicura che g sia una funzione, ovvero che associ ad ogni elemento del dominio uno e un solo elemento del codominio.

g si chiama funzione inversa di f, e si indica con .

Proprietà transitiva

se  A è in corrispondenza biunivoca con B, e B è in corrispondenza biunivoca con C, allora A è in corrispondenza biunivoca con C.

 

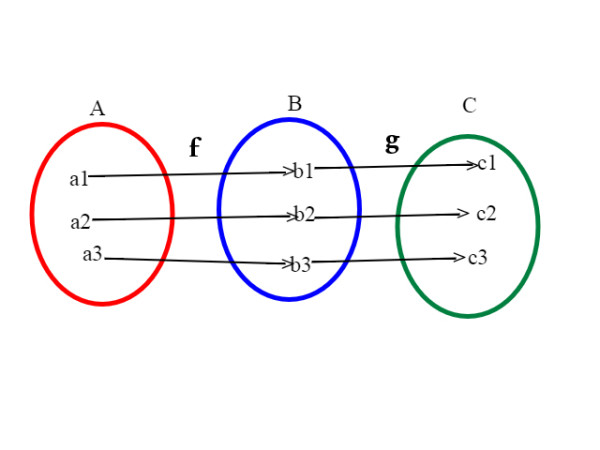
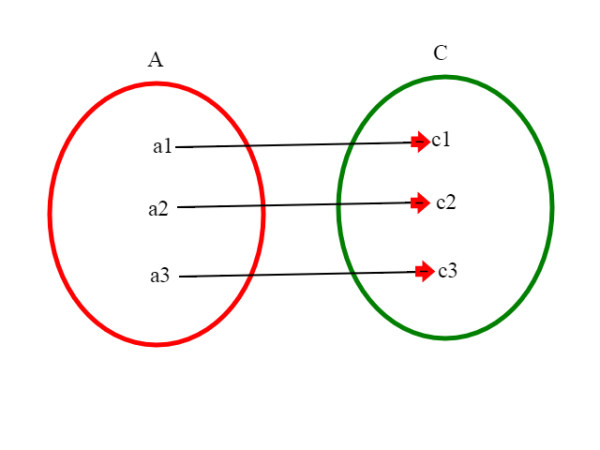
Per dimostralo rigorosamente basta definire una terza funzione z (che va da A a C) in questo modo:

z(a)=g(f(a)); questa funzione si chiama funzione composta di f e g.

(esempio: a1-->b1---->c1)

1 z è iniettiva

infatti se a1a2, essendo f iniettiva, f(a1)f(a2) e quindi essendo anche g iniettiva g(f(a1)) g(f(a2))

2 z è suriettiva.

Infatti se prendiamo un qualsiasi c che appartiene a C, sappiamo (g è suriettiva) che esiste un b tale che c=g(b); ma anche f è suriettiva, quindi esiste un a tale che f(a)=b; z(a)=g(b)=g(f(a)).

Quindi è una relazione d'equivalenza.

Nel caso della relazione di equivalenza fra insiemi che possono essere messi in corrispondenza biunivoca, la classe non è altro che il numero Cardinale dell'insieme.

Nel caso finito esso non è altro che quello che abbiamo sempre chiamato numero di elementi di un insieme; ma Cantor estese questa definizione anche agli insiemi infiniti.