Grazie ad Arturo e Umberto, posso ufficializzare la soluzione del quesito che avevo posto QUI e grazie a Zappi ora so che un certo Nicomaco di Gerasa, matematico e pensatore greco vissuto a cavallo tra il I e II secolo d.C., ci aveva già pensato parecchio tempo fa: da un lato un pochino mi dispiace, dall'altro mi fa piacere essere in buona compagnia 

Ma veniamo al sodo... tanto per cominciare, a riprova della mia inesperienza, avevo commesso un errore nella sintassi delle sommatorie! L'impostazione corretta è questa:

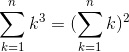    ed è ciò che vogliamo dimostrare

Notiamo subito che il secondo termine non è altro che la sommatoria di Gauss (ovvero la somma dei primi n numeri interi), quindi possiamo scriverla così:

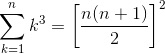       (1)

Ricordiamo che la sommatoria di Gauss è stata dimostrata da Umberto QUI utilizzando il principio di induzione che si usa nell'ambito dei numeri naturali e consiste nel dimostrare che se una certa proprietà vale per un certo numero naturale n' e, supponendo che sia valida per n si dimostra che è valida per n+1, allora vale per tutti i numeri naturali n>=n'.

A questo punto, possiamo proseguire con la dimostrazione di Arturo che utilizza proprio il principio di induzione

a) La (1) è vera per n=1. Infatti, per n=1 risulta:

b) Se la (1) è vera per n, è vera anche per n+1 ? Vediamo.

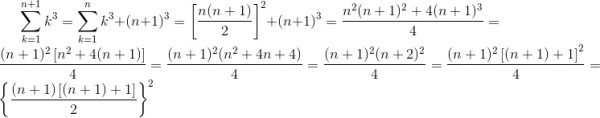
Cioè ho ottenuto:

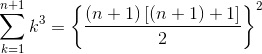
quindi la (1) è vera anche per n+1.

Allora, essendo verificate le condizioni a) e b), per il principio di induzione, la (1) è vera per qualunque valore di n.

Fatta la dimostrazione, non mi resta che ricordarvi come Gauss capì che la somma dei primi n numeri naturali è uguale al quadrato del semiprodotto di n e n+1... era poco più che un bambino e non aveva voglia di fare tutte quelle somme che il maestro assegnava alla classe per punizione (o per stare un po' tranquillo...). Zappi lo ha raccontato QUI!

Buona domenica a tutti, alla prossima!

Valentina

QUI trovate tutte le puntate de "La Maga dei Numeri"