Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Capisco benissimo che le coordinate sferiche siano una cosa abbastanza “noiosa” e appaiano poco importanti per comprendere i misteri del Cosmo. Tuttavia, esse sono di fondamentale importanza per eseguire calcoli e trasformazioni tra le posizioni apparenti degli astri. E’ un po’ come se volessimo scrivere un grande romanzo, ma considerassimo inutile o quasi imparare l’alfabeto…

Per cui vado avanti, comunque, e lascio un quiz per tutti coloro che amano la trigonometria e vogliano capire sempre meglio come si possa lavorare su una superficie sferica. Ricordiamoci che la superficie sferica -e le sue regole- sono la base della Relatività Generale… Concludiamo la nostra trattazione con il quarto sistema di coordinate celesti, particolarmente usato per le posizioni dei corpi celesti “vagabondi”.

La volta scorsa (qui) abbiamo già introdotto il piano dell’eclittica e la sua intersezione con la sfera celeste. Questo cerchio massimo è di estrema importanza perché rappresenta il percorso apparente del Sole durante l’anno. Altrettanto importante è il nodo ascendente tra l’eclittica e l’equatore, il celeberrimo punto d’Ariete (γ), da cui si misura l’ascensione retta del terzo sistema.

Le coordinate del terzo sistema sono perfette per dare nome e cognome alle stelle “fisse” (o quasi). Sono coordinate “teoricamente” sempre uguali (a parte le variazioni dovute alle perturbazioni agenti su tempi scala molto lunghi, su tutte la precessione degli equinozi) che permettono di stabilire molto bene i movimenti propri delle stelle (anche loro si muovono sulla sfera celeste, anche se di poco) e la parallasse annua.

La seconda permette di determinare la distanza di stelle relativamente vicine; il moto proprio ci dice quali sono i movimenti reali tra stella e stella, che risentono della rotazione differenziale della galassia, ma anche della loro vicinanza: più una stella è vicina e più il suo movimento rispetto a  noi diventa importante e macroscopico.

Coordinate, quindi, molto utili per la carta d’identità, ma anche per valutare qualsiasi piccolo spostamento non sistematico tra noi e le stelle teoricamente fisse.

Questo sistema di coordinate può andare ancora bene per i pianeti e gli oggetti del Sistema Solare, ma i loro movimenti rispetto a noi sono decisamente più macroscopici, dato che  anch’essi orbitano attorno al Sole.

Risulta ovvio che se i pianeti orbitassero tutti sul piano orbitale della Terra, i loro moti si proietterebbero solo e soltanto sull’eclittica. In realtà non è proprio così, dato che le orbite sono inclinate rispetto alla nostra, a volte di poco (pianeti maggiori), a volte anche di molto (asteroidi, comete, oggetti Kuiper Belt, ecc.).

In ogni modo, è indubbio che l’eclittica risulti un piano di riferimento migliore dell’equatore. Poco importa, in fondo, che i pianeti descrivano traiettorie circolari come le stelle a causa della rotazione del nostro pianeta sul suo asse. Molto più importante, per loro, è sapere di quanto si muovano sulla sfera celeste da un giorno all’altro. Proprio questi movimenti hanno, per secoli e secoli, costretto gli astronomi a inventarsi traiettorie strane, come gli epicicli, per finire, finalmente, con la visione eliocentrica.

Per non farla troppo lunga, è importante, perciò, introdurre un sistema di coordinate che faccia riferimento all’eclittica, che, come sappiamo molto bene, forma un angolo ε “abbastanza” costante rispetto all’equatore terrestre, pari a circa 23.5°.

Ricordiamo anche che proprio l’eclittica definisce le costellazioni dello Zodiaco, ossia quei gruppi di stelle che si trovano attorno a lei, indipendentemente se siano realmente vicine oppure no. Dato che i pianeti si muovo lungo l’eclittica, spostandosi di poco verso l’alto o verso il basso, ecco che nasce una parte fondamentale dell’astrologia,  quella interessata alla posizione dei pianeti rispetto a queste costellazioni, variabile durante l’anno. A noi, però, questa parte interessa ben poco…

Bando alle ciance e veniamo al nostro sistema (Fig. 13).

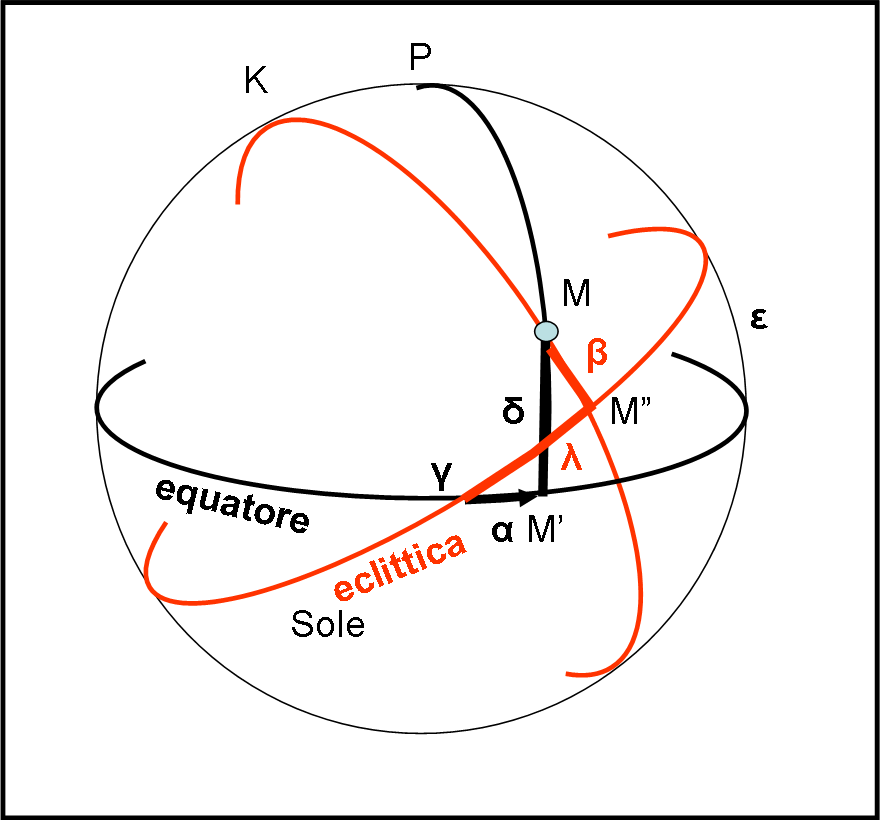
Il punto di riferimento lungo cui misurare gli archi di cerchio massimo dei pianeti lungo l’eclittica resta il punto γ, che può essere considerato fisso come fosse una vera stella. L’altro punto fondamentale, da cui far passare i cerchi massimi perpendicolari all’eclittica, è il polo dell’eclittica K. Ovviamente, l’angolo tra Polo Nord P e polo dell’eclittica K è ancora uguale a ε.

Tracciamo il cerchio massimo che passa per K e per l’oggetto M, fino a incontrare l’eclittica nel punto M”. La distanza in gradi, primi e secondi tra M” e M viene chiamata latitudine celeste e si indica con β. Essa è positiva sopra l’eclittica e negativa sotto. L’arco di eclittica tra il punto γ e il punto M”, anch’esso misurato in gradi, primi e secondi si chiama longitudine celeste e si indica con λ.

A questo punto, per permettervi di esercitarvi con la trigonometria sferica lascio a voi le formule che permettono il passaggio tra il terzo e il quarto sistema e viceversa. Basta trovare il triangolo  da risolvere e poi tutto risulta un semplice lavoro di routine…

QUI trovate tutti gli articoli su questo argomento