Categorie: Relatività
Tags: caduta libera campo gravitazionale forze apparenti principio di equivalenza relatività generale sistema accelerato sistemi di riferimento terzo principio dinamica verso la RG
Scritto da: Vincenzo Zappalà
Commenti:41
Einstein e l’imbianchino… ***
Questo articolo è stato inserito nella pagina d'archivio "La caduta libera" compresa nelle sezioni "Dinamica e meccanica" e "Relatività Generale"
Galileo ha avuto i suoi gravi, Newton ha avuto la sua mela e Einstein ha avuto il suo … imbianchino. Ebbene sì, sembra che l’idea più straordinaria che abbia avuto Einstein (secondo le sue stesse parole) gli sia venuta parlando con un imbianchino che era caduto da un’impalcatura di fronte al suo palazzo. Dopo di allora, forze apparenti, inerzia, accelerazione, gravità hanno iniziato a cambiare completamente la loro descrizione (in pratica sono scomparse) e, allo stesso modo, le conclusioni di Galileo e Newton sull’uguaglianza “fortunata” di massa gravitazionale e massa inerziale, è diventata l’ovvia conseguenza della gravità.
Non illudiamoci. Quello che sto per raccontare è solo una parte della Relatività Generale e va presa come un piccolo antipasto in vista di un pranzo ben più articolato e complesso. L’articolo vuole solo far vedere come il significato di inerzia e di forze apparenti diventi del tutto “trascurabile” o addirittura “privo di senso”, quando si arrivi all’equivalenza tra sistema accelerato e campo gravitazionale. Ci torneremo sopra, ripetendo varie cose, fino a inserire il tutto in un quadro veramente generale. Einstein ha faticato anni e anni, cercando di capire l’essenza del problema oltre che la sua descrizione. Possiamo, anzi dobbiamo, faticare un poco anche noi…
Le parole dette dal povero imbianchino, uscito solo un po’ malconcio, furono piuttosto banali, ma non per Einstein: “Mentre cadevo mi sono accorto di essere senza peso… una strana sensazione!”. Nella mente del grande genio scoccò la scintilla che stravolse tutte le leggi della dinamica newtoniana, ribaltandone il senso.
Ricordiamo che Galileo (grazie agli esperimenti con il piano inclinato) e Newton avevano già concluso che tutti i corpi cadono con la stessa accelerazione, il che comporta che la massa gravitazionale è uguale a quella inerziale e, ancora, che un corpo in caduta libera è soggetto a una forza apparente uguale e contraria a quella di gravità, tale da farlo sentire immobile nel suo sistema di riferimento (ne avevamo parlato anche QUI). Parliamoci chiaro: il peso (che è una forza), si sente solo quando agiamo sul terreno, o su superfici analoghe, che ci vietano la caduta verso il centro della Terra. Il peso, o –meglio- le conseguenze del peso, si sentono solo come risposta (terzo principio) della Terra verso di noi!
Einstein accetta tutto ciò, ma ribalta la situazione, assumendo che le “strane” evidenze osservative dei suoi illustri predecessori, non erano frutto di strane coincidenze, ma erano descritte completamente dalla natura stessa della gravità. Non è un caso che massa gravitazionale e massa inerziale sono uguali, come dicono le osservazioni, ma una conseguenza della nuova visione geometrica della gravità. Tutto è perciò da riscrivere, comprese le forze stesse agenti su una massa immersa in un campo gravitazionale o, comunque, accelerato
Einstein decide di rappresentare la gravità attraverso la geometria dello spazio, proprio in un momento in cui la Scienza ufficiale si sta dirigendo sempre di più verso il mondo sconosciuto e assurdo della meccanica quantistica . Una specie di “conservatore” a oltranza (anche se una delle prove osservative più importanti della MQ proviene proprio dal SUO effetto fotoelettrico ). Una rivoluzione “poco moderna”, che porta però a una teoria praticamente perfetta, che la MQ non riesce ancora a far sua.
Non vogliamo, però, parlare ancora dettagliatamente del principio di equivalenza sia debole che forte e nemmeno entrare a piedi uniti nella RG. Vogliamo solo fare un po’ di chiarezza sulle forze vere e apparenti che tanto sono servite al nostro Alberto per impostare la sua rivoluzione quasi inconcepibile per le altre menti, come ebbe a dire lo stesso Feynman.
Consideriamo, allora, due sistemi di riferimento e una scatola contenente due semplici palline di massa (ed energia) diverse. Cerchiamo di descrivere cosa succede se la scatola viene inserita in un ambiente PRIVO di gravità e in un campo gravitazionale.
Consideriamo la Fig. 1.
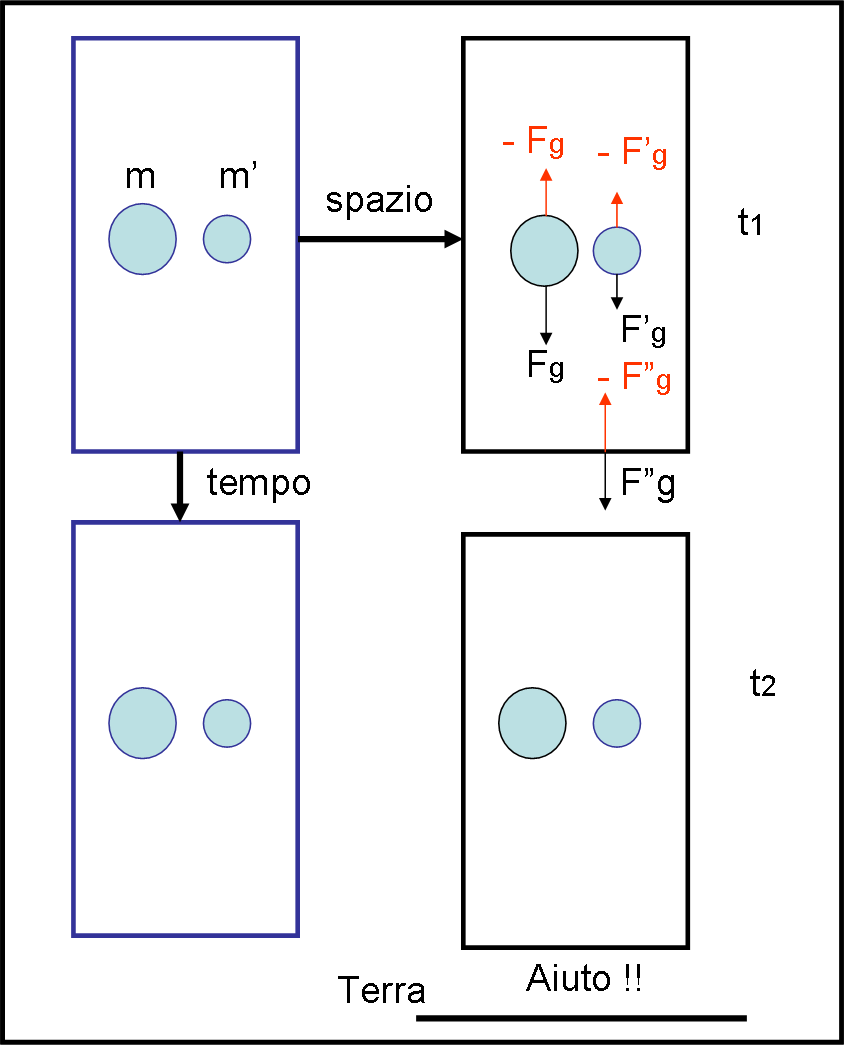
A sinistra abbiamo la nostra scatola talmente lontana da qualsiasi massa aliena che su di lei non agisce alcuna forza gravitazionale. Scatola e palline possono essere considerate ferme o, se preferiamo, in moto rettilineo uniforme, come dice il primo principio della dinamica. Le palline sono sospese nel vuoto, e tali rimangono dato che non vi è alcun movimento relativo uniforme tra scatola e palline (relatività ristretta).
L’osservatore esterno può vedere il tutto viaggiare a velocità costante o anche vedere il tutto immobile. Poco importa, dato che siamo di fronte a sistemi inerziali e il sistema della scatola può tranquillamente considerarsi fermo. Le palline non hanno peso… non solo, però, non sanno nemmeno cosa significhi la parola peso. Esse hanno solo massa, ossia energia (l’equivalenza tra massa ed energia l’abbiamo approfondita nelle lezioni di Dinamica Relativistica).
Al passare del tempo (verticale) niente cambia nel sistema sia se viene visto da fuori sia se viene osservato dal suo interno (in modo solidale con le palline e la scatola).
A destra, invece, spostiamo la scatola e la lasciamo in balia di un campo gravitazionale. Essa, insieme alle due palline, inizia a cadere verso il suolo sotto l’azione della forza di gravità. Il sistema non è più inerziale e tutto cambia se visto da fuori o dall’interno, seguendo, però, la regola fondamentale che il fenomeno meccanico (e anche fisico, dopo la RR) deve rimanere lo stesso.
Chi sta fuori non può che essere spaventato: la scatola e la pallina stanno cadendo a grandissima velocità… anzi, una velocità che aumenta istante per istante (l’imbianchino è caduto dall’impalcatura…).Tuttavia, se riusciamo a intervistare le palline (o l’imbianchino oppure il nostro Ciccio nell’ascensore), esse ci dicono che non pensano proprio di cadere: la parola peso è per loro del tutto sconosciuta. Tutto avviene esattamente come nell’esperienza fatta precedentemente nel vuoto.
Il problema esiste solo per l’osservatore esterno che deve cercare di spiegare come tutto ciò possa succedere. E’ lui che introduce una forza peso ed è lui che è costretto a far sì che le due palline si sentano perfettamente a loro agio. Le palline, in realtà non sentono la forza peso e, quindi, ciò implica che se veramente esistesse loro dovrebbero essere trattenute da una forza uguale e opposta. Chi ne ha veramente bisogno? Loro o l’osservatore esterno per cercare di avvalorare le proprie convinzioni?
Mi permettete di dire una cosa, piuttosto imbarazzante? Se tutta la massa della Terra fosse concentrata in un punto (cosa che già Newton aveva ipotizzato), la forza peso (o gravità, come preferite) non avrebbe alcun senso per le due palline e, di conseguenza anche tutti gli sforzi atti a cercare di descrivere l’intera faccenda con gli occhi di un osservatore esterno. Le palline sarebbero in caduta libera fino all'incontro con un punto in cui è concentrata tutta la massa della Terra. Una rappresentazione assurda che, però, aiuterebbe a vedere il tutto come una pura rappresentazione geometrica (ricordiamo la "strana" piastra calda). In fondo, basterebbe cambiare la visione complessiva della situazione…ed è quello che Einstein inizia a capire guardando l’imbianchino e parlando con lui… "il giorno più bello della sua vita!".
Cerchiamo di seguire il ragionamento dell’osservatore esterno.
Egli vede che tutto sta cadendo verso la Terra (scatola e palline) con la stessa velocità. Per lui è in azione la forza Fg, la quale impone un’accelerazione costante a tutto ciò che cade. Ha accettato l’idea che massa inerziale e massa gravitazionale siano uguali e quindi può dire che la forza, uguale alla massa moltiplicata per l’accelerazione (F = ma), utilizzi un massa che è la stessa che entra nella “sua” forza peso. La massa di chi cade sparisce e questo comporta che la velocità di qualsiasi oggetto (sempre più alta) rimanga la stessa per qualsiasi massa.
Non può, perciò, stupirsi più di tanto se alle palline sembra che tutto sia immobile come nel vuoto cosmico. Può anche spiegare alle palline che il loro non-peso “apparente” è dovuto all’entrata in azione, nel loro sistema di riferimento, di forze uguali e contrarie a quella di gravità ( -Fg), tali da farli sentire in completo riposo.
Il fenomeno fisico, anche se con qualche difficoltà, non cambia assolutamente. Le palline possono anche dargli ragione, ma ciò che sentono è molto più semplice da spiegare. Su di loro non si esercita nessuna forza o accelerazione. Tuttavia, se veramente esiste una forza peso, allora loro sentono prepotentemente la forza apparente che l’annulla completamente.
L’unica vera differenza è che l’osservatore esterno sa benissimo che al momento dell’impatto al suolo, le forze apparenti svaniranno, dato che il sistema in caduta libera non sarà più tale, e la forza gravitazionale darà luogo a una reazione uguale e contraria per il terzo principio della dinamica. Per lui la differenza tra sistema nel vuoto cosmico e sistema in preda al campo di gravità è decisamente grande. Non solo. Egli sa anche benissimo che questa reazione non dipende solo dall’accelerazione, ma anche dalla massa e il cratere formato dalle due sfere deve anche essere diverso (Fig. 2). Quello che conta non è più soltanto la velocità, ma anche la massa, come spiega bene l’energia cinetica (1/2 mv2).
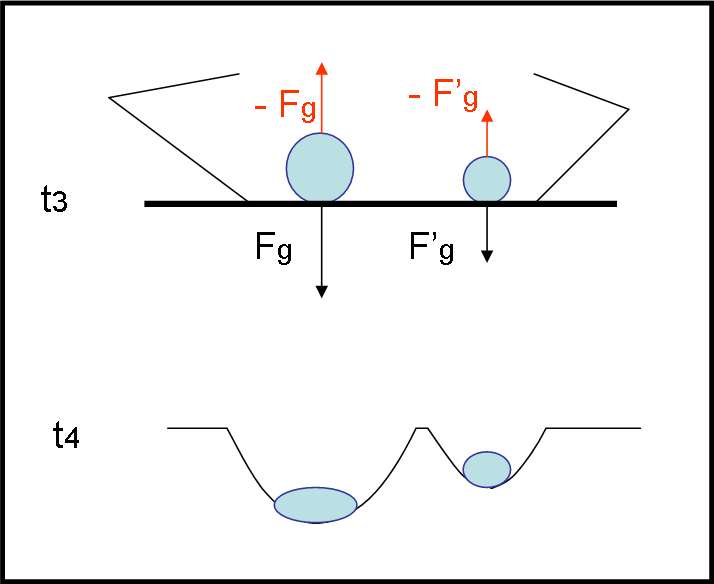
In poche parole, ben più generali, si può concludere che un corpo in caduta libera si comporta esattamente come un corpo che non è soggetto a nessuna forza o accelerazione. Se tutto il sistema segue la legge gravitazionale, nessuno può accorgersi della differenza delle due situazioni. L’idea di una situazione puramente geometrica comincia a farsi largo.
In pratica è stato detto che:
Un sistema di riferimento in caduta libera (ossia soggetto solo alla forza gravitazionale) e un riferimento inerziale sono del tutto equivalenti.
Possiamo anche lanciarci più in là e dire: “La geometria dell’ambiente è tale che conta poco la massa degli oggetti che stanno cadendo… loro seguono solo delle direzioni prestabilite. O -ancora più esplicitamente- poco importa quale sia la massa o l’energia coinvolta, dato che siamo di fronte a un problema puramente geometrico. Le masse non fanno altro che seguire le strade che la geometria ha preparato per loro. Avete presente uno scalo ferroviario con tanti scambi e tanti binari che vanno ognuno per i fatti suoi e a cui poco importa la massa del treno che sta arrivando? La differenza di massa e di energia si valuterà solo se avverrà uno scontro.”
Una visione completamente ribaltata rispetto a quella di Newton e Galileo. E tutto ciò grazie a un imbianchino caduto da un’impalcatura… Forza peso, forze apparenti, unicità dell’accelerazione stanno diventando ovvie conseguenze di una geometria particolare.
Tuttavia, possiamo tranquillamente procedere nel nostro tentativo di equivalenza ed estenderlo a un riferimento che non sia accelerato dalla gravità. Se esiste l’equivalenza di prima, dobbiamo continuare a confermarla.
Prendiamo la nostra scatola nel vuoto, fuori da ogni campo gravitazionale. Ci accorgiamo però che abbiamo a disposizione un motore, ossia un qualcosa capace di variare la velocità del sistema. Ovviamente, non può agire su tutto il sistema, ma solo sulla scatola. Le palline non possono risentire direttamente dell’accelerazione impartita alla scatola.
Tuttavia, succede qualcosa di strano… per chi sta all’esterno del sistema accelerato (Fig. 3, a sinistra).
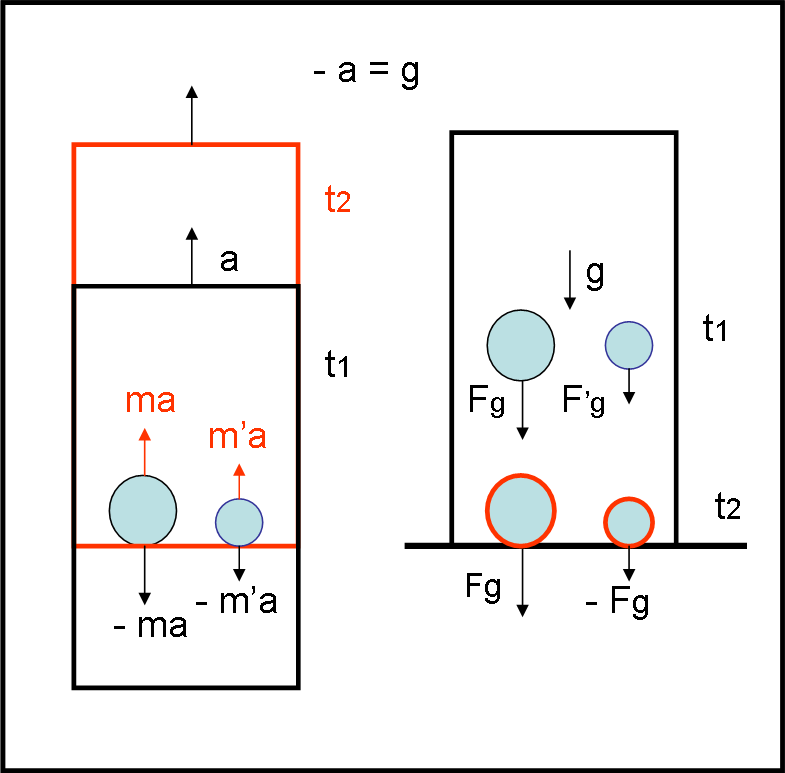
Le palline restano ferme (nessuno le ha accelerate o -se preferiamo- sono “inerti”) mentre si muove la scatola. Attenzione per muoversi deve accelerare, ossia cambiare la velocità precedente, sia che fosse zero sia che fosse un valore costante, lo stesso delle palline.
In breve, la parete di fondo non può che andare a scontrarsi con le palline. La palline subiscono un forza da parte della parete e per il terzo principio della dinamica esse devono rispondere esercitando sulla parete una forza uguale e contraria. Questa non è una forza apparente, ma una forza legata alla reazione. Una forza che vale proprio –ma e –m’a, se a è l’accelerazione della scatola.
Notiamo che a deve essere la stessa per le due palline, dato che è quella, unica, della scatola. Non sono invece uguali le forze subite dalle due palline, così come quando cadevano sulla Terra (o era la Terra che le veniva incontro come, adesso, il fondo della scatola?)
Portiamoci all’interno della scatola. Le palline vedono solo le pareti, che, ovviamente considerano ferme. Tuttavia, quella di fondo le si avvicina velocemente. Non possono che concludere che sono loro due che si stanno muovendo con una certa velocità diversa da prima, ossia che sono soggette a un’accelerazione che la porta verso il fondo della scatola. Stranamente, malgrado esse abbiano massa diversa, l’accelerazione è la stessa. Qualcosa di molto simile a quello che gli hanno raccontato mentre cadevano verso la Terra e si sentivano senza peso. Allora non si aspettavano l’impatto, ma adesso lo vedono arrivare con grande paura.
Adesso, finalmente, capiscono cosa sia la forza peso e che rischi comporti. Purtroppo, anche loro, subiscono lo scontro legato al terzo principio: la parete risponderà alla loro forza, con una reazione uguale e contraria che le farà fermare. Il fenomeno rimane identico nei due sistemi.
Dov’è la forza apparente? Beh, è sicuramente quella che sembra portarle verso il fondo, ma è così “fittizia” che è capace di creare una forza uguale e contraria nell’urto. In analogia a quanto è successo cadendo verso terra, sotto l’effetto della gravità, si può concludere che la forza fittizia è proprio qualcosa di identico alla forza di gravità! Questa volta, però, niente la viene ad annullare.
Possiamo dare il nome che vogliamo alle forze che abbiamo incontrato, ma resta il fatto che le palline si muovono geometricamente verso il basso per effetto di un’accelerazione, diretta o indiretta che sia. Se vediamo il sistema da fuori, le palline restano ferme e le viene incontro la parete. Se siamo all’interno del sistema sono le palline che si muovono fino a scontrarsi con la parete.
Bene, passiamo, nuovamente, a un sistema dominato dalla forza di gravità. Immaginiamo di prendere il nostro sistema inerziale e di poggiarlo a terra (Fig 3, a destra). La scatola non può muoversi dato che la parete di fondo imprime una forza contro il suolo e il suolo prontamente risponde con una forza uguale e contraria (terzo principio della dinamica). Attenzione: questo vuol dire che la scatola fa parte del sistema Terra. Le palline però, non sono poggiate a terra e quindi risentono della forza di gravità e cadono verso il suolo con la stessa accelerazione uguale a g.
La conclusione è che chi sta fuori vede le palline cadere verso il suolo, dominate da un’accelerazione ben definita g. La stessa cosa capita, però, anche alle palline che stanno dentro.
Finalmente tutto sembra uguale sia per un osservatore esterno sia per uno interno. Il fenomeno fisico è chiaramente lo stesso, senza dovere introdurre forze apparenti. La cosa è del tutto ovvia, dato che il sistema della scatola non è più un sistema diverso da quello terrestre. Si può togliere tranquillamente la scatola che fa ormai parte della Terra, essendo immobile su di lei. Le due palline cadono al suolo senza nessun aiuto esterno che cerchi di fermarle.
Possiamo veramente concludere che niente è assolutamente cambiato rispetto all’esperimento precedente: un sistema accelerato è del tutto equivalente a un sistema su cui agisce solo la forza di gravità. Possiamo cambiare le parole per spiegarlo, ma è indubbio che una nuova definizione della gravità potrebbe sistemare tutto sotto un unico ombrello, puramente geometrico, annullando forze reali e fittizie che si scambiano il ruolo continuamente.
Nasce il principio di equivalenza einsteniano:
Gli effetti dovuti all’inerzia, all’interno di una scatola uniformemente accelerata, in uno spazio non affetto da forze gravitazionali, sono equivalenti a quelli che si verificano in campo gravitazionale omogeneo. In altre parole: un’accelerazione uniforme crea un campo gravitazionale uniforme.
Notiamo bene la parola omogeneo… proprio la parola che ci farà curvare il mondo. La scatola non può essere considerata omogenea, dato che l’accelerazione di gravità g è costante solo LOCALMENTE. La gravità non è ancora del tutto pronta a essere sostituita da un sistema di riferimento accelerato.
Ribadiamo meglio questo concetto: anche se la scatola fosse grande, l’accelerazione che gli viene impressa è uguale per tutte le parti della scatola e, di conseguenza, anche l’accelerazione più o meno fittizia che sentono le palline. Se invece scatola e palline vengono inserite in un campo gravitazionale, le accelerazioni (di gravità) cambiamo da zona a zona della scatola. Per avere una perfetta equivalenza bisognerebbe considerare una scatola infinitesima che abbia una distanza unica dalla Terra e due palline per le quali siano trascurabili perfino le forze mareali.
Il principio di equivalenza si fa più sottile e le traiettorie di caduta geometriche sono costrette a deformarsi.
Bene fermiamoci qui, dato che l’intenzione è quella di affrontare la RG in modo ben più accurato. Considerate questo articolo sono un piccolo antipasto che serva, soprattutto, per interpretare in modo diverso le forze fittizie. Forze utilissime, sentite dagli oggetti, chiamate in tanti modi, che cessano di esistere quando finalmente la gravità viene veramente uguagliata a un sistema accelerato attraverso soltanto la sua geometria.
Le diverse visioni e proprietà delle forze fittizie spariscono come neve al Sole… e Pippo e il sottoscritto saranno pienamente d’accordo (spero ardentemente).
Non spaventatevi se questo articolo ha forse confuso un po’ certe idee. Mettetelo in un cassetto della memoria. Quando ci torneremo sopra sarà servito a puntualizzare i vari concetti, veri e propri mattoni per la costruzione della RG.
Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.
QUI trovate l'approfondimento dedicato alla Relatività Generale
QUI una spiegazione dell'assenza di peso in caduta libera adatta a neofiti e bambini di tutte le età
QUI la "vera storia" del piccolo Albert, molto intelligente ma anche un po' birbante, alle prese con un ascensore...






41 commenti
Dal letto di ospedale , a intervento concluso benissimo , col cellulare , mi dichiaro pienamente d'accordo e mi congratulo! Spiegazione semplice ma rigorosa !
Per le forze di marea c'è tempo. ..!
Ora devo solo pensare a...passare a vita migliore, ma non nel solito senso , bensì quello letterale !
Grande Pippo!!!
E, visto che mi sembri di buon umore, ti confesso che per me è una sorpresa prendere atto che anche la gravità possa essere considerata una forza fittizia (mi perdonerà Enzo se lo ha scritto da qualche parte in passato...)
Che ci vuoi fare... in questo Circolo, oltre ai super-preparati, ci sono anche persone come me ed è per questo che Enzo ci tiene tanto a procedere con estrema calma e a semplificare tutto al massimo, anche a costo di compiere, a volte, errori veniali (parlo in generale, non mi sto riferendo alla discussione sulla forza centrifuga) che possono infastidire esperti come te.
Un in bocca al lupo di tutto cuore per la tua nuova vita migliore!
Grazie Daniela ! Ma non sono un esperto , solo un appassionato.
Aspetta e vedrai , quando Enzo parlerà di come la materia curva lo spaziotempo!
Allora abbiamo qualcosa in comune... anch'io sono un'appassionata, solo con competenze tecniche decisamente inferiori alle tue!
Benissimo Pippo!!!!
Che bello saperti già in forma
Non vedo l'ora di combattere sullo spaziotempo tutto ondulato... Direi che ormai sei dei NOSTRI!
Il grande maestro ebbe nel suo lavoro,una grande stella polare,che lo guidò nelle sue entusiasmanti scoperte:”LA SIMMETRIA”.Nella relatività ristretta la simmetria è tra tutti gli osservatori che si muovono con velocità costante l’uno rispetto all’altro,quella generale mette il turbo,ed estende la simmetria a tutti i possibili osservatori,anche a quelli la cui velocità relativa non è costante.L’articolo ha messo in evidenza la simmetria dell’affresco scientifico,partorito da quella sublime mente,come fece, con la “Resurrezione “,Piero Della Francesca a Sansepolcro.Anche la scienza ha le sue vette estetiche ,quando riesce a spiegarne i suoi segreti meccanismi.
caro Gianni,
ti ricordavi questo articolo...?
http://www.infinitoteatrodelcosmo.it/2015/01/05/leffetto-fotoelettrico-un-processo-fisico-o-unopera-darte/
Caro Vincenzo,
l'articolo e' come al solito molto chiaro e persino alla mia portata (dubito lo sara' il seguito, ma per ora ci sono :-)).
Una cosa pero' mi risulta un po' ostica... o per lo meno in apparente contraddizione con l'esperienza quotidiana.
Tu dici che un oggetto in caduta non avverte il suo peso... e allo stesso modo non lo avvertono le palline che cadono insieme alla scatola. Ma a me pare che un oggetto che cade (o che accelera) avverta eccome l'accelerazione ... e la avverta anche se tutti riferimenti circostanti accelerano con lui. Per fare un esempio noi ci accorgiamo quando l'ascensore parte in discesa, anche se non c'e' alcun riferimento che possa mostrarcelo visivamente... e se accelerasse all'infinito continueremmo ad avvertirla, dico bene ?
Una sensazione credo molto diversa da quella che avverte l'astronauta in orbita, il quale non e' soggetto ad alcuna accelerazione, ma ad un equilibrio delle forze agenti su di lui. Dove sbaglio ?
Ciao Paolo,
in attesa che ti risponda Enzo, puoi dare un'occhiata a questo articolo che mette in relazione caduta libera e assenza di peso sia in ascensore che in astronave.
Mi ricordavo il quadro di Piero della Francesca,e che tu lo avevi lodato facendo delle considerazioni simili alle mie sulla "Flagellazione ",ma mi ero dimenticato di che cosa parlava,ottima occasione per un ripasso...Ero sicuro che comunque sarebbe stato apprezzato visto che oltre alle simmetrie in fisica,apprezzi questo grande maestro.
Paolo,
tu cosa intendi per "sentire" l'accelerazione? Noi abbiamo solo dimostrato che essere accelerati con un'accelerazione uguale a -g è come essere immerso in campo gravitazionale di accelerazione uguale a g.
Se sei in caduta libera non senti alcun peso, mentre lo senti comunque se l'ascensore ti rallenta dato che si oppone alla caduta libera, anche se accelera leggermente. Quando dovesse arrivare a un'accelerazione uguale a g, saresti in caduta libera così come lo sarebbe anche l'ascensore. Finché l'ascensore non raggiunge g, egli agisce come un qualcosa che ti impedisce di cadere.
Ti chiederei di farmi un esempio preciso, per potere vedere esattamente cosa senti e perché lo senti...
Mh. Per "sentire l'accelerazione" intendevo semplicemente "avvertire" la forza che ci costringe ad accelerare.
Provo a fare un esempio. Se noi (il nostro corpo) e la famosa scatola con dentro le palline siamo immobili nel vuoto, lontano da qualsiasi campo gravitazionale. In assenza di alcuna forza non c'e' alcuna accelerazione... noi, la scatola, le palline, stiamo li fermi senza peso.
Supponiamo adesso che vicino a noi (diciamo qualche migliaio di km) appaia per incanto un bel pianeta, e che noi e la scatola con dentro le palline si finisca immersi nel suo campo gravitazionale. Le palline, la scatola, noi stessi si inizierebbe a cadere verso la superficie... cioe' ad accelerare continuamente fino a schiantarci al suolo.
La mia considerazione forse puramente sensoriale, e' basata sull'intuizione che accelerare continuativamente (cioe' essere soggetti ad una forza), anche se i nostri riferimenti accelerano con noi, e' qualcosa di avvertibile diversamente dal caso in cui non c'e' alcuna forza (oppure quelle che ci sono si annullano, come nel caso dell'orbita). Ma forse sbaglio...
caro Paolo,
Tu stai ipotizzando proprio il caso descritto... Chi sta sull'astronave comincia a muoversi per effetto della gravità del pianeta, accelerando con g (sia l'astronave che chi gli sta dentro) e non può notare alcuna differenza rispetto a prima. Caduta libera = immobilità nel vuoto. Si sente un'accelerazione quando vi è inerzia rispetto a chi accelera... (schiacciamento contro il sedile o cose del genere).
Ci ho riflettuto ancora... mi sa che sbaglio.
Questo il ragionamento: spesso l'accelerazione viene avvertita dal nostro corpo perche' la forza ci viene trasmessa da un altro corpo (un'auto, un'astronave... il suo sedile)... e quindi il nostro corpo viene schiacciato o tirato...
Ma se la forza (es la gravita') agisce su tutto il nostro corpo contemporaneamente (dalla pelle agli organi interni), allora non saremmo in grado di capire se siamo immobili o stiamo accelerando, e quindi l'astronauta in orbita (forza nulla) dovrebbe provare esattamente la stessa sensazione di quello che (assurdamente) si lasciasse cadere verticalmente verso la superficie da un immaginario trampolino spaziale fermo (non orbitante), e non si renderebbe quindi conto di stare accelerando verso la superficie...
Correggimi se dico stupidaggini (e perdona la banalita').
Credo di avere capito, forse, a cosa tu, Paolo, ti riferisca quando parli di sensazione dovuta all'accelerazione di gravità. E' la sensazione di cadere che ognuno di noi ha avvertito almeno qualche volta nel sonno ? Oppure quella che si prova quando si precipita di botto da quelle paurose giostre di un parco dei divertimenti ? Il fatto è che, con riferimento al quiz dell'acqua e il bicchiere, lasciandoli cadere entrambi liberamente, si osserva che l'acqua non fuoriesce più dal buco presente sulla parete del bicchiere...
Caro Leandro,
in effetti ero partito proprio immaginando quel tipo di situazione: non potevo credere che l'astronauta in orbita provasse la stessa sensazione di quelli che sull'ottovolante sperimentano l'accelerazione di gravita'.
Ma credo di esserci arrivato: la sensazione di caduta e' dovuta al repentino passaggio da una situazione in cui il nostro peso e i nostri organi sono sorretti dalle gambe o dalla struttura del nostro corpo a uno in cui di colpo non lo sono. Cioe' se gia' fluttuassimo (cioe' non fossimo attaccati e seduti su nulla), e la forza agisse su ogni punto di noi (come la gravita') non ci accorgeremmo di accelerare ...
Dici bene Paolo e dice bene anche Arturo... Le sensazioni sono sempre causate dallo "scontro" tra parti inerti e parti accelerate... Il bicchiere ne è proprio la prova lampante... L'acqua non sente nessuna caduta rispetto al bicchiere, dato che sono entrambi in caduta libera. ma, quando toccheranno terra... allora sì!
Un articolo scritto davvero molto bene che lascia molto riflettere. C'è però una frase di cui ignoro (per limiti miei) completamente il senso.
La riporto qui:
"permettete di dire una cosa, piuttosto imbarazzante? Se la massa della Terra fosse concentrata in un punto (cosa che già Newton aveva ipotizzato), la forza peso (o gravità, come preferite) non avrebbe alcun senso per le due palline e, di conseguenza anche tutti gli sforzi atti a cercare di descrivere l’intera faccenda con gli occhi di un osservatore esterno"
Sinceramente non l'ho capita. Potrei avere maggiori lumi? Perché se la massa della Terra fosse concentrata in un punto la forza peso perderebbe di significato? La forza pesa è diretta conseguenza della gravità. Quindi cosa cambia se quest'ultima sia concentrata o meno in punto?
Grazie a chi mi saprà chiarire questo dubbio.
Complimenti Vincenzo Zappala'.
caro Andrea,
la mia era una frase paradossale, che deriva da quanto detto precedentemente:
"Parliamoci chiaro: il peso (che è una forza), si sente solo quando agiamo sul terreno, o su superfici analoghe, che ci vietano la caduta verso il centro della Terra. Il peso, o –meglio- le conseguenze del peso, si sentono solo come risposta (terzo principio) della Terra verso di noi!
Ipotizzando un punto, non potremmo sentire il peso inteso in questo modo e va cambiato l'approccio
Ah ok Vincenzo, mi era sfuggito il collegamento con la frase precedente. Effettivamente non potrei sentire la forza peso della Terra senza neanche poggiare i piedi su di essa. Anche perché é difficile immaginare di poter mettere i piedi su un puntino minuscolo. Ed ecco che il fattore geometrico ha più logica. È questo il senso, giusto?
esattamente Andrea! Scusa, ma in realtà, avrei dovuto spiegarmi meglio... Grazie per il preciso commento...
Ma figurati Vincenzo, ce ne fossero persone come te capaci di rendere molto semplici concetti di assoluta complessità.
Ti posso fare solo una domanda sul concetto della gravità intesa non come forza, ma come deformazione spazio-temporale?
Provo ad essere il più chiaro possibile.
Non riesco a cogliere bene il concetto di come la deformazione dello spazio indotta da una massa possa avere come conseguenza quella di attirare verso di sé un'altra massa che si trova nello stato inerziale di QUIETE.
Mi spiego meglio: a me ad esempio torna bene che la Terra ruoti attorno al Sole come effetto della curvatura spazio-temporale indotta dalla nostra stella, perché in questo caso la nostra cara Terra segue un "binario" curvo creato dal Sole, un effetto chiaramente geometrico. Fin qui mi è chiaro. Per i corpi in moto il discorso é semplice, e cioè che la traettoria che il corpo segue mentre è in moto è quella "disegnata" per lui dalla distorsione dello spazio-tempo. Quello che non mi convince invece è l'attrazione di un corpo da FERMO, come ad esempio la mela di Newton. Anche per la mela, così come per la Terra, c'è un binario precostituito, tuttavia non capisco come faccia la mela a muoversi su questo binario se non c'è nessuno che la spinge. Non so se sono stato chiaro. Un po' come il movimento di un treno. Anche il treno ha una traiettoria prestabilita. Anche il treno, come la mela e la Terra, segue la traiettoria di un binario, retto o curvo che sia, ma se all'inizio non c'è qualcosa che lo spinge a muoversi, questo rimane fermo sui binari (primo principio della dinamica). Ti trovi? Perché ciò non avviene anche per la mela o qualsiasi altro oggetto fermo? Come fanno questi oggetti a passare dallo stato di quiete a quello di moto per un puro effetto geometrico?
caro Andrea,
la mela di Newton non cade perché c'è una forza che si oppone alla gravità, ossia non la fa proseguire nei binari spaziotemporali. Questa forza è quella di legame della materia che la tiene unita al'albero (e sono forze ben più potenti della gravità). Infatti, se si rompe questo legame, la mela cade... E' come quando apri un paracadute o fai partire un razzo verso lo spazio: il motore si oppone alla curvatura spaziotemporale e il razzo si allontana.
In realtà non esistono corpi fermi (il moto è sempre relativo). La curvatura della relatività generale si accentua sempre di più andando vicino ala massa centrale. Devi andare molto lontano per non subire alcun effetto, ma ci sarà un'altra massa capace di farla scivolare sui suoi binari. Tuttavia, la stessa RG ipotizza un corpo al di fuori di ogni curvatura (come un treno in piano) e infatti Einstein paragona proprio la caduta libera a un corpo fuori da ogni campo gravitazionale.
Si Vincenzo, è vero che la mela quando è attaccata si oppone alla forza di gravità e resta quindi ferma, ciò che io non comprendo è come possa iniziare a muoversi ed essere trascinata giù nel momento in cui questa si stacca dal ramo. O meglio, non lo comprendo considerando la gravità come curvatura spazio-temporale. Se qualcuno trancia in un colpo solo il ramo su cui è attaccata la mela, io mi aspetto che questa resti ferma fino a quando non ci sia qualcuno a spingerla per farla scorrere sul binario spazio-temporale.
Se io piazzo un treno fermo su un binario questo non cammina se non c'è una forza che lo spinge a farlo, ti trovi? Perché invece la mela inizia a muoversi sul "binario" spazio-temporale anche quando parte da uno stato di quiete?
Ti può sembrare un ragionamento assurdo e contorto, ma non è così
Non so più come spiegarlo... La mela è sempre all'interno di un binario e sta subendo l'accelerazione dovuta a quel binario. Se venisse resa libera dalla forza che la tiene sul ramo, sentirebbe immediatamente l'accelerazione del binario e quindi sarebbe costretta a muoversi. L'unica differenza è che non è una forza che fa cadere la mela, ma solo il fatto che la mela si trova su una "superficie" inclinata e, quindi, se la lasci libera lei comincia a cadere lungo la superficie inclinata fino a che il terreno si oppone alla sua caduta.
Il treno non cade verso il centro della terra solo perché il terreno lo sostiene con una forza uguale e contraria al suo "binario" (il suo binario è occupato e deve fermarsi).
Ultimo tentativo...
la mela si trova in caduta verso il buco creato dalla massa terrestre: se è attaccata al ramo è il ramo che blocca momentaneamente la caduta fino a che non la lascia libera di CONTINUARE il suo moto verso la massa. Se è già caduta è il terreno che gli vieta di continuare nel suo moto verso il buco. Il treno è già caduto sulla terra e non può proseguire. Non mischiare motori che fanno camminare sulla terra. Devi pensare solo al moto che trascina verso il centro di massa (per quello avevo parlato di un punto). Anche un bob che cade lungo il suo binario può essere fermato se gli metti un masso davanti... Ogni cosa è costretta a cadere verso il centro, ossia verso quel punto in cui tutta la massa è concentrata: una specie di imbuto. Per stare fermo dovresti essere talmente lontano da considerare nullo l'imbuto... Lo puoi pensare solo teoricamente, dato che dove finisce l'imbuto della Terra comincia quello della luna e se li elimini tutti e due c'è quello del Sole... Se la mela si staccasse e sparisse immediatamente la terra, la mela cadrebbe verso il Sole...
caro Andrea,
provo a inserire una figura che potrebbe aiutarti... Nota bene che il disegno si riferisce a uno spazio a una dimensione, mentre , in realtà, lo spaziotempo ne ha quattro... per cui bisogna fare uno sforzo interpretativo per generalizzare uno schema giocoforza incompleto e semplificato...
Caro Vincenzo, intanto ti ringrazio per lo sforzo e l'impegno che stai mettendo per cercare di inculcarmi il concetto in testa.
Più leggo e rileggo i tuoi interventi però e più mi viene difficile comprendere l'analogia tra i binari classici terreni e quelli spazio-temporali.
Quindi, siccome immagino tu abbia sparato tutte le tue cartucce, invece di ripartire da zero, estrapolo dal tuo intervento la frase che in me genera i dubbi maggiori e ci focalizziamo solo su quella.
Ecco: "la mela si trova in caduta verso il buco creato dalla massa terrestre: se è attaccata al ramo è il ramo che blocca momentaneamente la caduta fino a che non la lascia libera di CONTINUARE il suo moto verso la massa".
Il punto in cui non ci troviamo è esattamente questo: tu consideri come concetto base che tutti gli oggetti sulla terra siano in caduta libera, quindi consideri tutti gli oggetti costantentemente in uno stato di moto e mai di quiete, in quanto perennemente accelerati dalla gravità e solo momentaneamente bloccati da altri ostacoli (il ramo per la mela e il terreno per il treno).
La questione sui cui batto io però è: prima che un oggetto vada in caduta libera ed inizi a percorrere il binario curvo spazio-temporale, deve esserci un momento nella sua storia in cui si trovava in uno stato di quiete? E se si, cosa lo spinge ad un certo punto a muoversi? Cioè, riprendendo l'immagine che hai postato: se la mela (prima parte), invece che stare sul ramo apparisse dal nulla in uno stato di quiete (quindi non in caduta libera) esattamente sullo spigolo in cui lo spazio (il binario) si incurva, quale forza la spingerebbe a muoversi su quel binario? Capisci il senso del mio discorso? La mela appare dal nulla in uno stato di quiete esattamente sul punto in cui inizia la curvatura (prima parte della tua immagine). Ecco, a quel punto ci deve essere un input iniziale che la spinge verso il basso. E da chi é dato questo input iniziale? Semplicemente dalla curvatura stessa? Ma se dipendesse solo dalla curvatura, allora la mela salirebbe e scenderebbe a suo piacimento ripercorrendo il percorso curvo andata e ritorno, proprio come fanno i treni normali.
Quindi il focus del discorso è questo: come si passa da uno stato di quiete ad uno in moto all'inizio di un binario curvo spazio-temporale (prima parte dell'immagine considerando una mela comparsa dal nulla in uno stato di quiete).
caro Andrea,
non c'è nessuno spigolo tra spaziotempo curvo e lo spaziotempo in cui si può stare in quiete. Se la Terra fosse da sola nell'universo, tutte le mele che tu potresti aggiungere cadrebbero verso di lei. Ricorda che la velocità di fuga è quella cosa che deve portare la mela all'infinito. Dato che i corpi massicci sono tantissimi, la quiete si potrebbe avere solo bilanciando due o più rotaie. In poche parole non esiste pianura nello spaziotempo: c'è sempre una qualche discesa. Potrebbe servirti la definizione di punti lagrangiani: quelli dove non si cade né su una stella né sull'altra... ma non perché non ci sono binari, ma perché non riesci a preferirne uno dei due e resti in bilico.
La forza di gravità (e quindi la curvatura spaziotemporale dovuta a una massa) è l'interazione più debole, ma ha un raggio d'azione infinito!!!
Ok, adesso mi torna meglio.
Quindi dalla tua ultima frase si potrebbe concludere che i sistemi inerziali di fatto non esistono? Se la forza di gravità ha un raggio d'azione infinito vuol dire fondamentalmente che qualsiasi corpo nello Spazio, chi più e chi meno, è in un continuo stato di accelerazione.
caro Andrea,
in linea teorica sì... ma tu pensi che un muone che arriva a 0.9 c possa essere influenzato dalla gravità terrestre? La RG non fa altro che accostare tante RR fino a che non si arriva a un punto critico.
Perfino Galileo che usava far cadere acqua in un bicchiere considerava la nave inerziale rispetto alla Terra. Ma nessuno dei due è veramente inerziale...
Tutta la fisica classica si basa sui sistemi inerziali pur sapendo che nessun sistema può essere veramente inerziale. Il paradosso dei gemelli considera il motto della Terra inerziale, così come l'astronave... e siamo nella RR...
"....la parete di fondo imprime una forza contro il suolo e il suolo prontamente risponde con una forza uguale e contraria"
Bene, ma quanto PRONTAMENTE?
Intendo dire se nessun segnale puo andare più forte della luce (anche se avevo letto in qualche libro di B.Greene che forse hanno trovato qualche particella che sembra andar più veloce,ma tralasciamo) anche la risposta del suolo deve avere UN TEMPO....giusto? Ovvero non una risposta istantanea.
E seconda domanda, se ogni forza è conseguenza di un campo, e ogni campo è mediato da una qualche particella...quale razza di strana particella mi fa sentire questa reazione uguale e contraria?
Spero siano 2 domande intelligenti per consacrarmi per la prima volta al tuo Blog Vincenzo!
caro Stefano,
benvenuto innanzitutto!
In realtà, quella che si chiama reazione è qualcosa che avviene a livello elettronico, come ho in parte spiegato qui:
http://www.infinitoteatrodelcosmo.it/2019/01/01/ce-tanto-spazio-laggiu-fondo-soluzione-del-quiz-fine-anno/
Quando pensiamo di toccare qualcosa vuole solo dire che si esercita una repulsione tra gli strati esterni degli elettroni della nostra mano e di quello che si "crede di toccare". Quindi la risposta di reazione è praticamente immediata, coinvolgendo gli elettroni che si respingono.
Che la gravità abbia bisogno di particelle trasmettitrici come le altre forze è il PROBLEMA della grande unificazione, ancora irrisolto. Di sicuro, comunque, anche i supposto gravitoni viaggiano alla velocità della luce come si è dimostrato con le onde gravitazionali.
Questo fatto penso proprio che risponda a entrambe le domande. E, comunque, l'informazione che si trasmette non può certo viaggiare più veloce della luce. Se vai tra i quiz ne troverai parecchi che si riferiscono alla trasmissione del segnale di un urto lungo un certo corpo. Ovviamente, date le velocità, si tratta di relatività ristretta...
Ad esempio questo:
http://www.infinitoteatrodelcosmo.it/2017/07/14/soluzione-del-quiz-del-bacherozzo-cattive-notizie/
Se ho ben capito una definizione per un sistema inerziale è un sistema in caduta libera ovvero un sistema ove valgono le leggi di Newton in particolare la prima( anche se non mi è chiaro come in questo caso valgano le leggi di Newton) la Terra può solo considerarsi per approssimazione un sistema inerziale perché ruota su se stessa e orbita intorno al sole. Nell'universo non esistono sistemi in quiete o in moto rettilineo uniforme come la fisica classica definisce i sistemi inerziali. Mi corregga professore e le sarei grato se mi illustrasse esempi in merito
Caro Maurizio,
Come esempio ti potrei dare tutti gli oggetti che mantengono la propria quantità di moto costante oltre un certo limite non rivelabile o trascurabile. Il fotone lo fa... ma anche molte altre particelle. L'importante è che sia costante la velocità e la massa si possa considerare costante (RR). Quando non capita più siamo di fronte alla RG.
Se un punto materiale è libero, cioè non sottoposto a forze o a forze che diano come risultante una forza nulla, allora persevererà il suo stato di quiete o di moto rettilineo uniforme finché esso non viene perturbato. Questa è la definizione di sistema inerziale perfetto. Un oggetto che è sufficientemente lontano da masse (spazio intergalattico, ad esempio) si avvicina perfettamente alla definizione. In parole povere, è inerziale tutto ciò che non subisce accelerazioni. Se eliminiamo gli attriti anche sulla Terra possiamo simulare sistemi inerziali, come fece Galileo notando che su una nave in movimento nulla cambia rispetto a chi sta sulla terraferma. L'importante è che il moto si svolga a velocità costante. La gravità è controbilanciata e non varia tra chi sta in nave e chi sta a terra.
La caduta libera simula molto bene un sistema inerziale in cui non vi è moto alcuno (l'accelerazione è la stessa per tutti coloro che stanno nell'ascensore). Tuttavia, se l'abitacolo è grande va tenuta in conto la differenza di accelerazione di gravità tra punti diversi dell'abitacolo. Tutto sta nella precisione che si pretende. Per moltissimi fenomeni gli effetti gravitazionali sono trascurabili rispetto a quelli dovuti alla non inerzialità perfetta dei sistemi. Il muone segue la RR perfettamente, dato che il disturbo dovuto alla gravitazione nella sua caduta verso il suolo è nettamente trascurabile rispetto agli effetti legati alla velocità elevatissima e alla corrispondente dilatazione dei tempi e contrazione delle lunghezze.
Quindi anche tutto ciò che è interno ad un astronave che orbita intorno alla Terra è un sistema inerziale: tutto fluttua quindi ogni massa o è sottoposta ad una forza risultante nulla o non è sottoposta ad alcuna forza.
Mi corregga se ho scritto inesattezze
esattamente... Michele. Tu pensa a quelli che stanno nella stazione spaziale. Loro risentono e come della forza di gravità. Ma risentono anche, nel loro sistema di riferimento, di una forza uguale e contraria di tipi inerziale (centrifuga). Quindi sono praticamente in continua caduta libera... La stazione spaziale continua a cadere verso la Terra, come già aveva compreso Newton.
quindi ogni sistema in caduta libera è inerziale, come ad esempio i voli in caduta libera sugli AERIBUS per simulare l'assenza di peso, i proiettili lanciati da una bocca di fuoco durante la loro traiettoria ecc.
Purtroppo la credenza popolare associa a queste esperienze l'assenza di gravità ma la gravità c'è sempre è l'assenza di peso che si manifesta.
Ricordo nel lontano 1974 alle Lezioni di FISICA 1 facoltà di ingegneria de La Sapienza ROMA le spiegazioni sulla differenza tra massa inerziale e gravitazionale molto complesse e non facilmente comprensibili, Lei ha saputo trattare l'argomento in maniera semplice ed esauriente
Grazie professore in caso di chiarimenti sugli articoli del sito chiederò delucidazioni
In questo caso, Michele, la credenza popolare è generata e alimentata da chi avrebbe il dovere di correggerla: basta scrivere "zero gravity" (o qualcosa di simile) su un motore di ricerca per rendersene conto.
Guarda, per esempio, questo video dell'Agenzia Spaziale Europea, con una mia domanda che giace lì da oltre un anno senza uno straccio di risposta...
https://www.youtube.com/watch?v=_bQAMjYmwhI
caro Michele,
innanzitutto ti ringrazio di essere dei "nostri"...
Posso aggiungere che alla vecchia classica definizione newtoniana di sistema inerziale si potrebbe oggi, con l'avvento della RG, aggiungere "Un sistema è inerziale se, rispetto ad esso, un corpo, lasciato a se stesso, persevera nel suo stato di quiete o di moto rettilineo uniforme". E così diventa del tutto ovvia l'esperienza dell'ascensore e del moto della stazione spaziale.
Certamente, come dice Daniela, bisognerebbe far di più per correggere l'idea di "gravità zero". In fondo basterebbe fare l'esempio della Luna. Essa è sicuramente in balia della gravità terrestre (questo lo sanno tutti) e allora come potrebbe essere a gravità zero un oggetto decisamente più vicino, come la stazione spaziale? Magari la Cristoforetti avrebbe anche potuto accennare alla questione oltre che fare varia pubblicità ...
A onor del vero, la pubblicità è della rivista Le Scienze che ha riportato il tweet della Cristoforetti: lei si è limitata a commentare la didascalia di un libro scolastico.
Riconosciamole almeno il merito di averci provato, anche se non ha citato l'esempio della Luna... sempre meglio di Nespoli che, per spiegare la gravità ai bambini, definisce la ISS "un posto incredibile, fuori dal mondo, dove non c'è più la gravità"...
https://www.youtube.com/watch?v=ABILEFSJUhY
Ho visionato i siti citati da Daniela e sono rimasto meravigliato che esistono testi scolastici ove si parla di assenza di gravità sulle stazioni spaziali.
Nespoli poi poteva evitare di parlare di assenza di gravità per spiegare ai bambini l'esperienza sulla ISS, bastava che parlava di assenza di peso come alla fine del discorso ha citato.