Categorie: Matematica
Tags: angolo al centro angolo alla circonferenza quiz trave triangolo rettangolo
Scritto da: Vincenzo Zappalà
Commenti:5
Soluzione del quiz della trave appoggiata **
Il mio tentativo di “incastrare” i più bravi, proponendo uno studio di funzione, quando il tutto è risolvibile con semplici considerazioni geometriche, è fallito miseramente e … ne sono contento! Sono, inoltre, particolarmente grato ad Arturo che, pur capendo l’inghippo, si è cimentato, comunque, nello studio analitico (in due modi), ottenendo, ovviamente, la soluzione geometrica. Propongo direttamente i suoi manoscritti come ottimo esempio di trattazione matematica (anche se praticamente inutile). Lo so, faccio troppi complimenti ad Arturo… ma quando ci vuole, ci vuole… Complimenti anche a Gimar e Leandro, ovviamente…
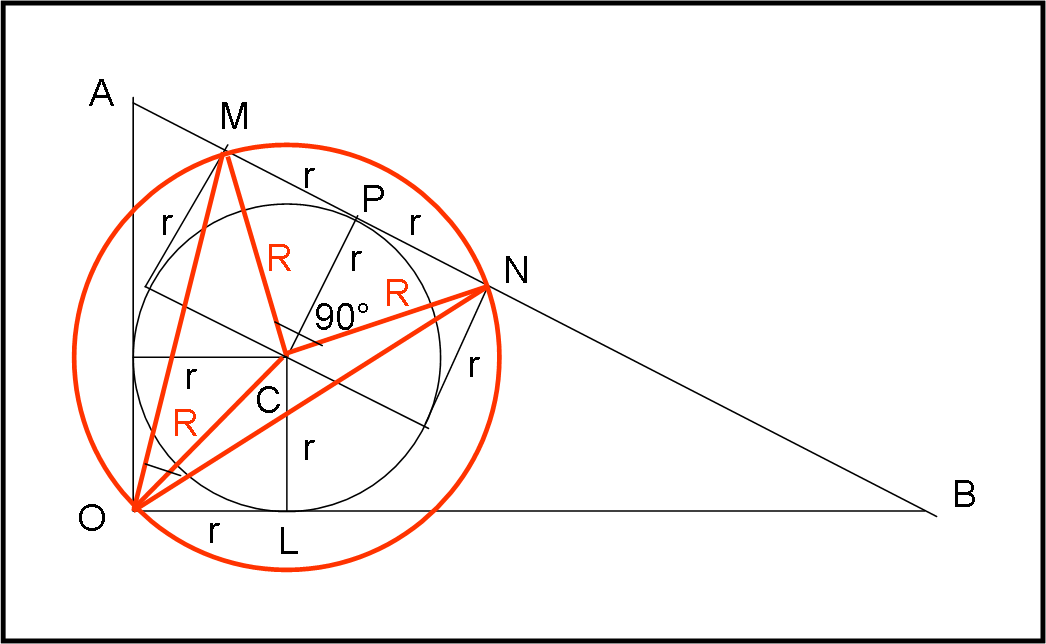
La figura, volutamente elaborata per trarre in inganno, può essere facilmente schematizzata come segue: abbiamo un triangolo rettangolo in O, qualsiasi, e il suo cerchio inscritto. Proiettiamo il diametro sull’ipotenusa e troviamo due punti M e N. Si vuole dimostrare che l’angolo MON è sempre uguale a 45°.
La dimostrazione è semplicissima, costruendo qualche triangolo isoscele supplementare. CPM è uguale al triangolo CPN, dato che sono rettangoli per costruzione e hanno i cateti uguali a r (raggio del cerchio iscritto di centro C). Deve allora valere che:
CM = CN
Disegniamo anche il triangolo rettangolo CLO. Anch’esso, per costruzione, ha i due cateti uguali a r e quindi è uguale ai due triangoli precedenti. Ne segue che:
CM = CN = CO = R
Tracciamo la circonferenza di raggio R e centro C. Essa deve contenere i tre punti M, N e O.
L’angolo al centro, sotteso dall’arco MN (MCN) è uguale a 90° (somma di due angoli di 45°). Ne consegue che lo stesso arco deve sottendere un angolo alla circonferenza (MON) che è la metà di quello al centro, ossia 45°. E questo risultato è del tutto indipendente da come si sia scelto il triangolo rettangolo iniziale…
Adesso voglio inserire, senza alcun commento, ciò che Arturo mi ha inviato e che ha un suo interesse intrinseco. Si può usare la matematica anche per dimostrare l’ovvio…
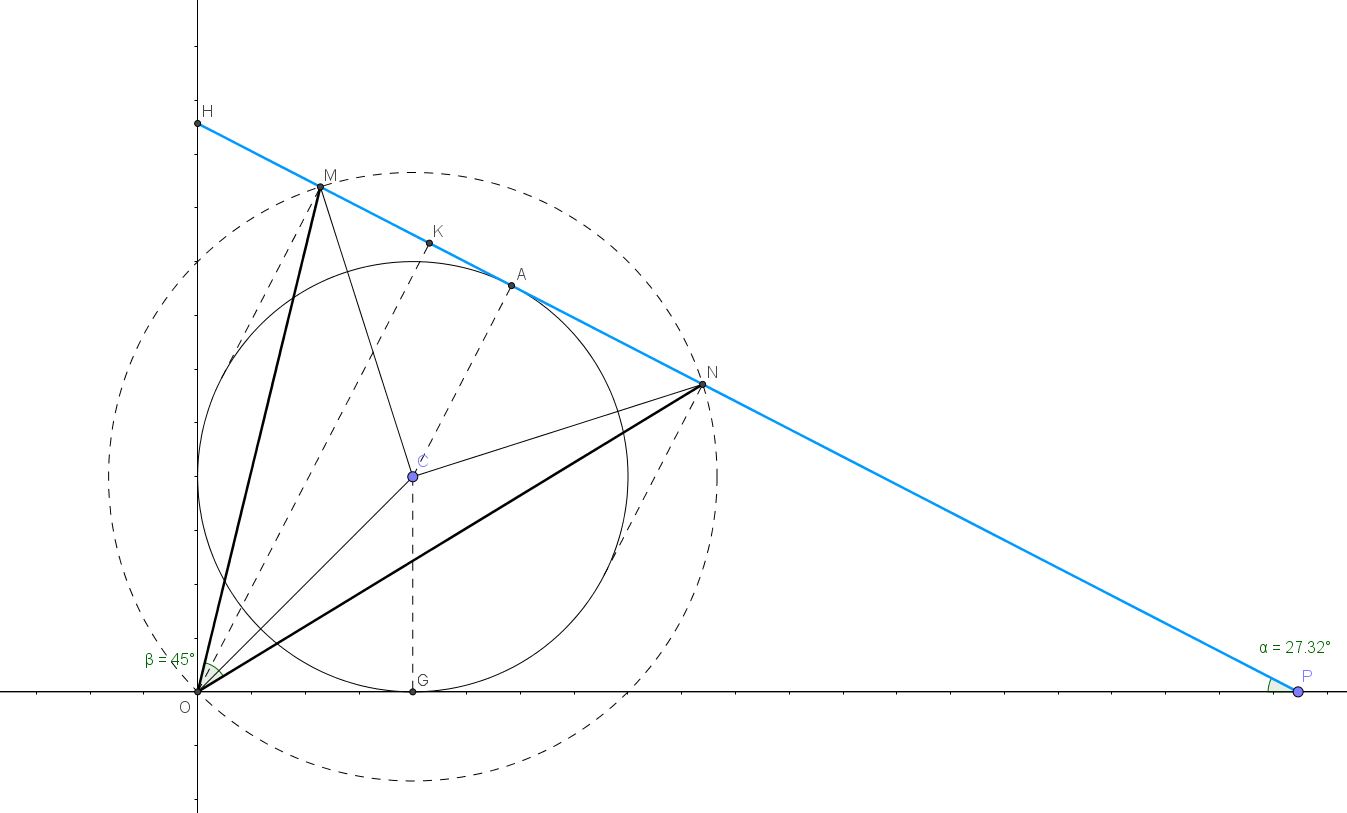
Per seguire meglio la sua trattazione, è bene utilizzare la sua figura che ha qualche lettera cambiata..
La prima è una dimostrazione estremamente rigorosa…
La seconda una versione molto semplificata …
Anche conoscendo la via geometrica, ha voluto divertirsi… Magnifico. Non dimentichiamoci, inoltre, che Arturo è colui che ha comprato il palloncino e l’ha legato in macchina! Non ci credete? Guardate QUI
Che dire?. È veramente un esempio di lettore e collaboratore (diciamo pure AMICO) perfetto di questo circolo! Lui ha capito proprio tutto di noi… e ci ha accettato con la giusta allegria. Si deve sempre imparare divertendosi o -se preferite- divertirsi imparando.
Grazie Arturo per essere uno dei “nostri”…
Il QUIZ lo trovate QUI
5 commenti
Grande Arturo che ha sperimentato con perfetto metodo galileiano il comportamento del palloncino in auto, sfidando le "malelingue" del piccolo paese in cui vive
però, però... non ha terminato l'esperimento... siamo ancora in attesa di sapere come si comporterà il palloncino con lo sportello posteriore aperto 
Grazie Vincenzo, semplicemente cerco di applicarmi alle materie che mi piacciono, come sono certo facciano tutti coloro che si avvicinano e poi seguono questo Circolo. E' inevitabile
Piccola precisazione per coloro che fossero interessati ai miei appunti pubblicati da Vincenzo: bisogna fare riferimento alla figura che pubblicai nel commento al quiz, che riporto qui per comodità (alcune lettere sono diverse). Per vederla bene bisognerebbe ingrandirla facendo click direttamente QUI:
Daniela, avevo provato con i vetri dei due sportelli posteriori abbassati, ma non cambiava praticamente nulla. Credo perché la presenza degli schienali dei due sedili anteriori dell'auto ostacolavano il deflusso dell'aria dell'abitacolo verso la parte posteriore e anche perché l'aria che magari cercava pure di uscire fuori dai finestrini posteriori, a causa del moto dell'auto in avanti e conseguenti turbolenze, restava dentro. Mi ripromettevo di fare la prova con il portellone posteriore completamente aperto e con i due schienali abbassati. Comprendi che sarebbe stata una prova impossibile da fare in presenza di una possibilità anche minima che qualcuno mi vedesse...
Per cui ho temporeggiato, ma nel frattempo il palloncino si è sgonfiato (si, la membrana di cui in genere è fatto il palloncino ha una sua porosità al gas elio e questo lentamente fugge via....) e non ho ancora avuto modo di tornare dall'amico per farlo rigonfiare.. Ma prima o poi lo farò, anche perché ho scoperto un negozio di articoli per parties e feste varie, in cui vendono palloncini di tutte le misure e a volontà 
Insomma... ti sei preparato per i prossimi QUIZ
Voglio vedere come la metterai con le deformazioni spaziotemporali
caro Arturo,
ho inserito la tua figura nel testo...
Fantastico! Allora non perdo le speranze
Cosa ne dici di usare un palloncino a forma di cuore?? 