Ho collaborato solo tecnicamente alla stesura di questa appendice sul paradosso relativistico: il missile va a vuoto! , ideata però interamente dall'amico Pippo, anche se per motivi organizzativi la pubblicazione proviene da mio account.

 

Il diagramma di Minkowski allegato è relativo al riferimento di B assunto come riferimento di quiete, e A che si muove verso destra rispetto a B. Facciamo un esempio numerico che aiuta a capire quanto finora detto.

Premetto che assumiamo c=1  , quindi si ha che la coordinata temporale ct si può scrivere semplicemente t , e il tempo risulta misurato in m (metri) . 1m di tempo è semplicemente il tempo che la luce impiega a percorrere 1m di spazio. Trovato un certo tempo in metri , per ritornare ai secondi è sufficiente dividere il numero trovato  per  c = 0.30m/ns ( la luce impiega infatti 1 miliardesimo di secondo= s per percorrere 0.30 m) .
Premesso ciò , prendiamo dei valori arbitrari per la lunghezza propria delle due astronavi A e B, uguale per entrambe : = 50 m , e prendiamo la velocità relativa delle stesse : v=0.6c = 0.6  ( questa velocità è adimensionale, essendo uguale al rapporto che talvolta si trova indicato con   : non è necessario introdurre simboli in più ) .

Il fattore di Lorentz risulta quindi : .
In quel che segue si suppone, ripeto, B in quiete e A in moto relativo verso destra rispetto a B, nella direzione dell’asse spaziale x ; ma nulla avrebbe impedito di fare il contrario, cioè assumere A in quiete e B in moto verso sinistra : quello che conta è la velocità relativa tra le due navi .

Come sappiamo, la lunghezza della nave A vista (cioè misurata ) da B , risulta contratta , ed è pari a : = 50/1.25 = 50*0.8 = 40 m . È vero anche che la lunghezza di B, misurata da A , è contratta , e in questo caso ha lo stesso valore in quanto le lunghezze proprie sono uguali.
Indichiamo senza apice le coordinate (x,t) del riferimento B di “quiete” , e con apice le coordinate (x’,t’)  del riferimento A in “moto” , come normalmente si fa .

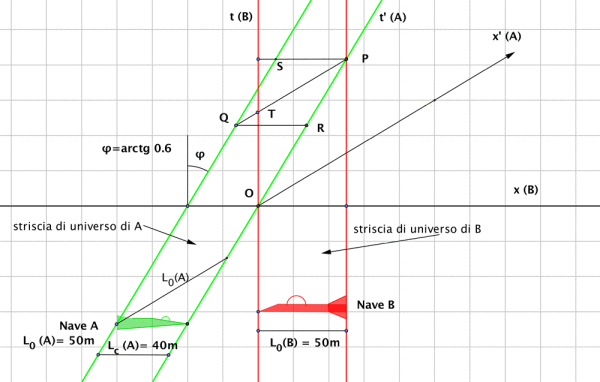
Definiamo “striscia di universo” della nave B la striscia di piano compresa tra le due rette temporali dei due estremi, avanti e addietro, che sono parallele all’asse t di B . Tale asse sul disegno appare verticale , e il suo corrispondente asse spaziale x è disegnato ad esso perpendicolare. Anche la nave A traccia sul piano una sua striscia di universo, che ora è parallela all’asse dei tempi t’ del riferimento di A . Quindi l’asse t’ forma un angolo con l’asse t , tale che : .
Sembra che , sulla carta, gli assi x’ (A) e t’ (A) non siano perpendicolari, ma non è vero . Questo succede, come sappiamo, perchè la geometria del piano di Minkowski NON è euclidea : si dice che è pseudo-euclidea , cioè iperbolica .
In realtà anche gli assi x’ e t’ sono ortogonali , come sappiamo.
Tracciate le due strisce di universo , di B e di A , esse si intersecano in vari punti. Assumiamo come origine delle coordinate spazio-temporali il punto in cui la linea di universo della punta di A interseca la linea di universo della punta di B . Per chiarezza notiamo una cosa importante : la lunghezza contratta di A , vista da B , si ottiene sezionando la striscia di universo di A con una “retta di simultaneità” di B , parallela all’asse x (B) . È chiaro invece che, sezionando la striscia di universo di A con una retta di simultaneità di A stesso, si ottiene la lunghezza propria di A :  (anche se sul disegno sembra più lunga!) .

I punti notevoli del diagramma di Minkowski sono quindi :

1)Origine delle coordinate O : è, ripeto, l'evento in cui la linea di universo della testa di A incontra la linea di universo della testa di B . Quindi , in entrambi i riferimenti , le coordinate di O sono nulle , sia spazio che tempo : (x,t) = (0,0) = (x’,t’)

2) Evento P : è l'evento in cui la testa di A incontra la coda di B . Risulta :  (infatti la punta di A si sposta della lunghezza propria di B) . La coordinata temporale in B vale :

questi sono metri di tempo , che in secondi valgono :  .

Quali sono le coordinate di P nel riferimento di A ? Basta applicare le trasformazioni di Lorentz :

 

e questo è ovvio, visto che P è sull'asse dei tempi t’ di A .

questo risultato : 

corrisponde al noto risultato che l'intervallo di tempo proprio è minore dell'intervallo di tempo coordinato tra due eventi dati. Gli eventi dati in questo caso sono l’evento O e l’evento P . Questa relazione fondamentale sarebbe meglio esprimerla usando i differenziali :
. (con  si indica di solito il tempo proprio, che qui è indicato con apice t’) .

Risulta , mettendo i numeri : = 222.22 ns

3) quando si verifica l'evento P , contemporaneamente per A deve verificarsi l'evento Q , cioè lo sparo del missile dalla coda di A . Questa è l’ipotesi di base del problema. Allora dobbiamo trovare le coordinate di Q , dapprima in A , e poi trasformarle con Lorentz nel riferimento di B .
Il tempo di Q in A è quindi :

La coordinata spaziale di Q in A è  :

in quanto   , come prima detto .

Trasformiamo con Lorentz inverso le coordinate , dal sistema in moto A al sistema di quiete B :

cioè:

come è evidente anche dal disegno, risulta che nel riferimento di B :  .

Il valore numerico è :  277.77 ( 1-1.25*0.36) ns = 152.77 ns

La coordinata spaziale è data da :

come c'era da aspettarsi , la coordinata spaziale di Q è negativa perchè Q si trova alla sinistra dell'asse dei tempi di B (vedere disegno) .

Risulta, mettendo i numeri : = - 0.25*50 m = -12.5 m

Dunque , il missile sparato dalla coda di A (evento Q) è alla sinistra della striscia di universo della nave B , e non la colpisce, pur avendo la nave A una lunghezza contratta rispetto a quella propria . Per B , quando la coda di A è nell'evento Q la testa è nell'evento R, non in P . Le coordinate di R in B si trovano subito :

Il tempo di R è uguale al tempo di Q , in B : = 152.77 ns

l'ascissa di R in B si trova sommando a quella di Q la lunghezza contratta della nave A : = (-12.5 + 40) m = 27.5 m

Come si vede , , cioè per B la nave A ha sparato il missile troppo presto, quando la testa di A non era al traverso della coda di B (evento P) ma a poco più della metà , in R , che dista dalla testa di B solo 27.5 m .

Volendo, si possono determinare le coordinate di R in A , sempre con le trasformazioni di Lorentz .
Per esempio, si vede subito che , in quanto R è sull’asse dei tempi di A . Quanto vale ? Provateci .

Questi risultati confermano che la contemporaneità tra eventi è diversa, in sistemi di riferimento in moto relativo. Mentre, per A, Q è contemporaneo a P, per B l’evento Q è contemporaneo a R . Il punto essenziale è che l'evento Q è alla sinistra della striscia di universo di B . Per colpire B , A dovrebbe aspettare che la sua coda, da cui parte il missile, coincida almeno con l’evento T sul tratto PQ .

Il significato degli eventi T ed S, segnati in figura, è il seguente :

-nel riferimento di B , la coda di A è in S quando la testa è in P. Infatti, SP non è altro che la lunghezza contratta di A , vista da B (sezione della striscia di universo verde con una retta di simultaneità di B )

-nel riferimento di A , la testa di B è in T quando la coda è in P . Infatti , TP non è altro che la lunghezza contratta di B, vista da A ( sezione della striscia di universo rossa con una retta di simultaneità di A ) . Non deve meravigliare che TP sembra, sul disegno, più lungo di .

Se uno vuole divertirsi, può calcolare le coordinate di T ed S nei due riferimenti.

Volendo, si potrebbe poi assumere il riferimento di A come quello di quiete , e il riferimento di B in moto verso sinistra, e disegnare un (apparentemente) diverso diagramma di Minkowski. Come si fa ? Basta “allargare a forbice” i due assi t’, x’ di A , mettendo t’ verticale e x’ orizzontale sul disegno , e conseguentemente far ruotare gli assi di B , e le striscie di universo, mantenendo invariati gli angoli che t forma con t’ e x forma con x’ . In questo nuovo diagramma , la nave A è in quiete , la nave B si muove verso sinistra con velocità -v .
Questo “allargamento a forbice “ degli assi t’,x’ ha una nome : si chiama rotazione iperbolica .