Un altro piccolo, ma fondamentale, passo verso la relatività generale. Il principio di equivalenza che pone sullo stesso piano un sistema accelerato e un sistema sotto l’effetto della gravità comporta conseguenze quasi inaspettate anche sul tempo. La famosa "piastra" torna in campo…

Andiamo a comprare (o ci fabbrichiamo) due orologi veramente precisi e portiamoci all’interno di un’astronave. Uno lo inseriamo nella parte “alta” (A) e uno nella parte “bassa” (B) di Fig. 1.

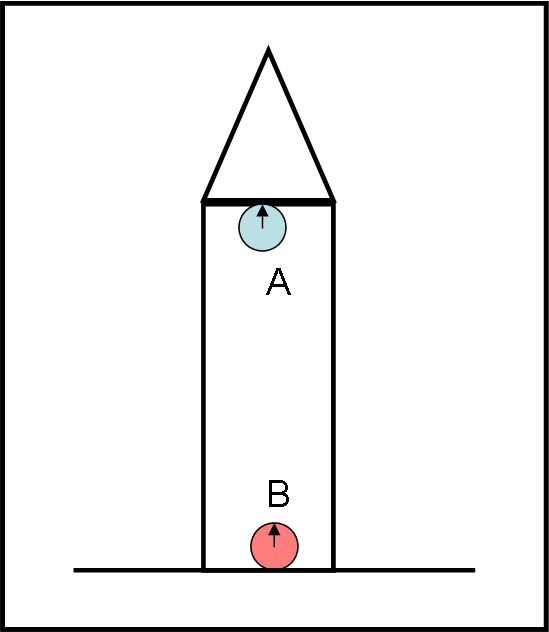
Prima di partire li controlliamo attentamente. Sembra che siano veramente perfetti. Per sicurezza estrema, facciamo un controllo ulteriore: l’orologio A spara ogni secondo un raggio di luce. L’orologio B lo riceve e può confermare che i segnali luminosi sono intervallati esattamente di un secondo. Un osservatore si mette vicino all’orologio A e uno vicino all’orologio B. Magnifico, si può partire accelerando in modo costante.

Continuiamo l’operazione di prima (non si sa mai e poi ce l’ha consigliato un certo Einstein), ossia a ogni secondo che passa l’orologio A invia un segnale luminoso verso la parte posteriore.

La situazione, all’istante dell’invio della prima luce, è quella rappresentata in Fig. 2a (tempo zero), mentre quella dell’arrivo del segnale in B è la Fig. 2b. Per semplificare la faccenda immaginiamo che per arrivare in B la luce abbia impiegato proprio un secondo. Il che vuol dire che A può inviare il secondo segnale verso B, che lo riceve in Fig. 2c. L’osservatore A ha mantenuto perfettamente  il secondo di intervallo. Per notare meglio le differenze, la lancetta dei nostri orologi si sposta di 90° ogni secondo (sono o non sono ultra precisi?).

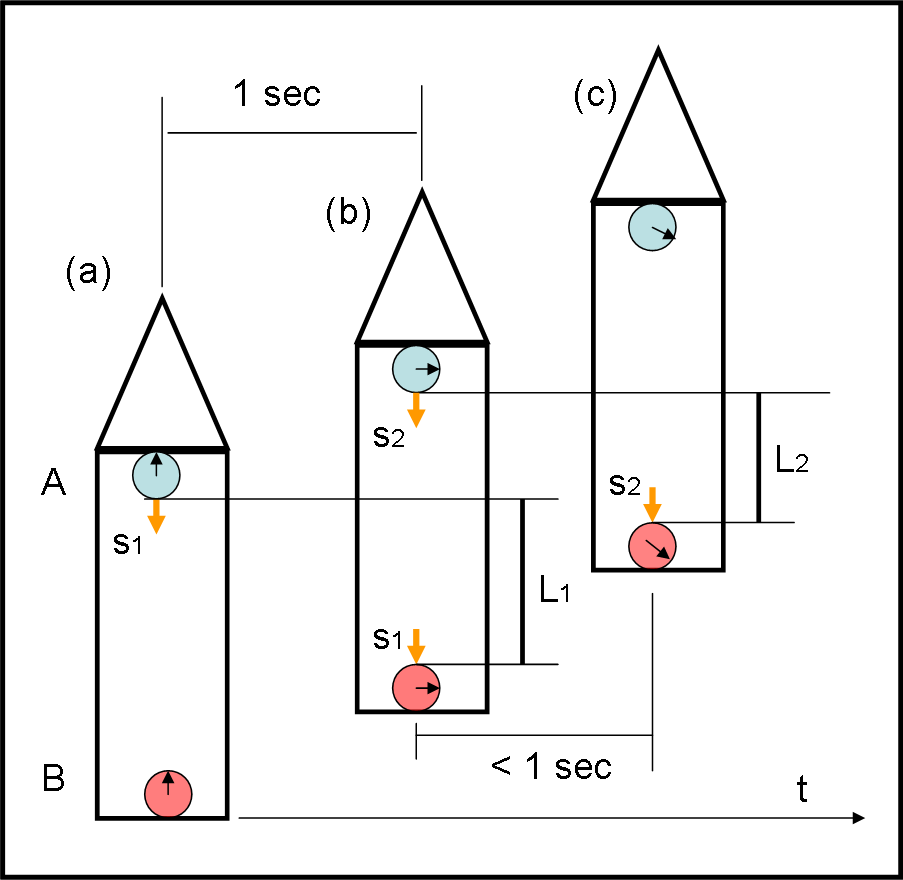
Cosa nota l’osservatore in B? Ammettiamo, come già detto, che l’orologio B riceva il primo segnale proprio nell’istante t = 1 secondo. Non gli resta adesso che attendere che arrivi il secondo segnale. E’ pronto a giurare che la luce arriverà dopo un altro secondo.

E, invece no. Accidenti, l’osservatore in B deve ammettere che c’è qualcosa che non va! Per lui non è assolutamente passato un secondo, ma decisamente meno! Sa benissimo che il suo orologio non sbaglia un colpo. E’ costretto a concludere che l’orologio di A va più veloce del suo! Ha infatti inviato i due segnali, intervallati tra di loro di meno di un secondo. E il risultato continua a verificarsi al passare del tempo.

La faccenda sembra strana, ma non poi tanto. Immaginiamo che anche l’orologio B invii un segnale luminoso ogni secondo. Questa volta anche l’osservatore posto vicino ad A rimane alquanto sorpreso. Il secondo segnale gli arriva dopo un intervallo maggiore di un secondo. Non può che concludere che l’orologio B va più lento del suo, come vediamo nella Fig. 3a,b,c.

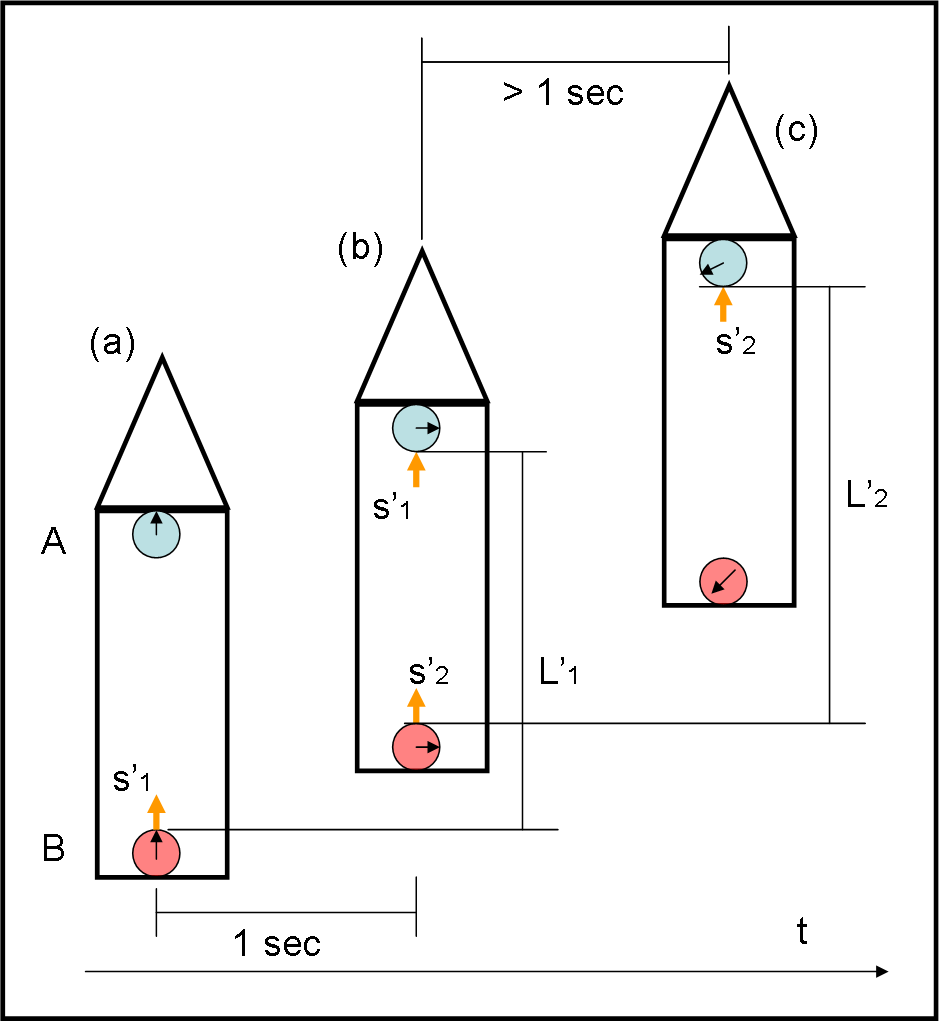
In poche parole arrivano entrambi allo stesso risultato: per l’osservatore in B è l’orologio A che va più velocemente, per l’osservatore in A è l’orologio B che va più lentamente. Perfetto nella sua stranezza, dato che all’inizio sembravano andare così bene entrambi. Non sono più in accordo tra loro e quello più “alto” segna un tempo maggiore (l’orologio va più in fretta) o -se preferiamo- è quello in B che segna un tempo minore (l’orologio va più lentamente). In fondo, concordano tra di loro: uno dei due è sicuramente andato in “tilt”.

Avessero tenuto conto dell’accelerazione, non si sarebbero certo stupiti e non avrebbero dato la colpa agli orologi. Il segnale di A impiega sempre meno tempo per arrivare in B in quanto B va sempre più velocemente incontro alla luce. Il segnale di B impiega, invece, più tempo ad arrivare in A, dato che A si allontana sempre più velocemente. La variazione di velocità è costante, il che vuol dire che lo spazio percorso cresce col tempo (legge del moto uniformemente accelerato).

Notiamo, infatti, che non sarebbe successo niente se l’astronave si fosse mossa a velocità costante il segnale sarebbe partito e arrivato sempre a intervalli di un secondo (Fig 4a,b,c)

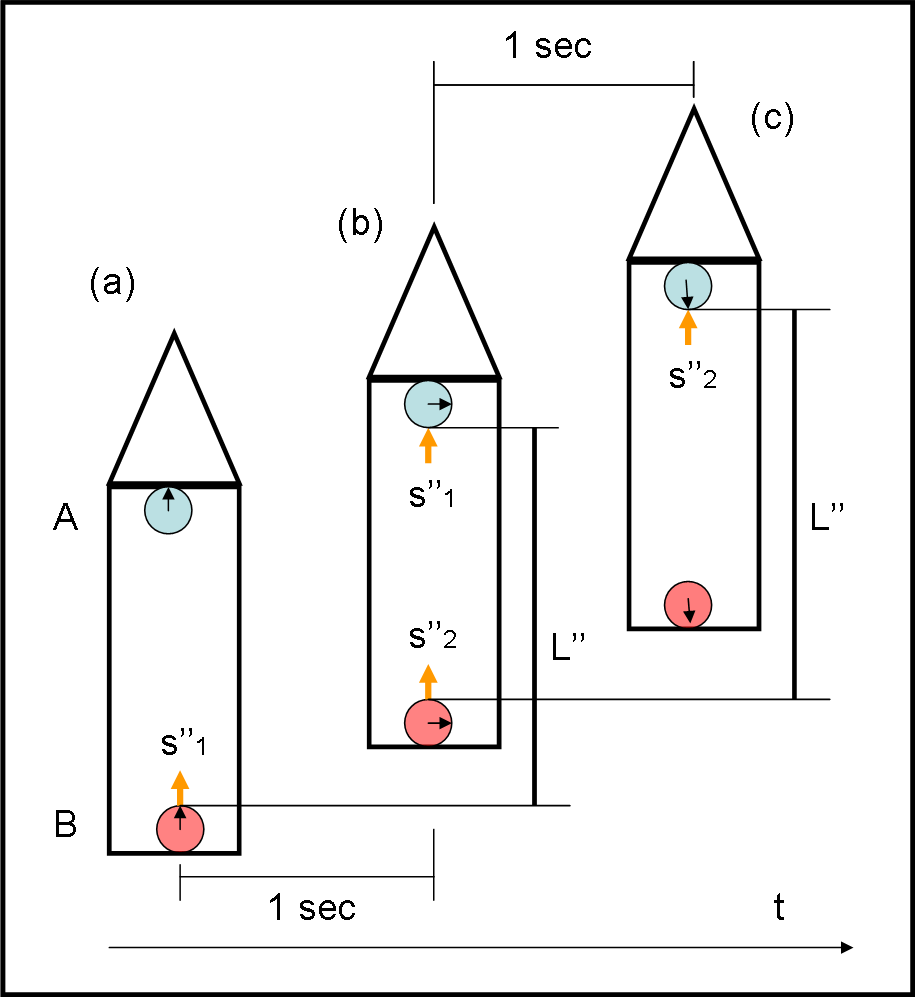
Insomma tutto bene, basta ragionarci un po’ sopra. Sì, tutto bene se … non ci fosse il principio di equivalenza!

Accidenti… se questo capita in un’astronave accelerata, deve anche capitare in un campo gravitazionale: l’orologio più alto deve girare più velocemente di quello più in basso!

E questo è un fenomeno perfettamente uguale a quello che succedeva nello spazio della strana piastra calda. Più ci si allontanava dal centro e più la lunghezza del righello unitario aumentava. In questo caso più si va lontano dalla massa (chiamiamola pure “piastra”) e più l’orologio gira veloce, ossia il tempo misurato risulta più lungo.

Einstein era talmente sicuro del suo principio di equivalenza che non poteva fare altro che accettare il fatto che gli orologi misurano un tempo diverso ad altezze diverse dalla Terra. Non solo gli orologi, ma anche i battiti del cuore e tutti i fenomeni fisiologici…

Solo un genio, sicuro di sé, poteva proseguire lungo questa direzione che sembrava un’assurdità perfino più grande del mondo di Alice. Einstein lo fece e gli esperimenti gli continuano a dare ragione. Lo spazio e il tempo, ossia lo spaziotempo è curvato dalla gravità.

La prossima volta, per chi ha il desiderio di entrare nei dettagli, vedremo quanto la gravità incide sul tempo segnato da un orologio sia artificiale che naturale…

In pratica, la relatività generale è tutta qui…

Abbiamo visto che una piastra molto strana (definita attraverso la sua massa/energia) causa uno spaziotempo curvo. Basta allora scrivere la relazione che vi è tra le caratteristiche della curvatura e le caratteristiche della piastra. Questa relazione prende il posto della ben più famosa F = ma.

Come sempre, la verità è di una semplicità disarmante… la difficoltà sta nello scriverla in un linguaggio comprensibile agli umani. L'Universo la conosce e la segue perfettamente.

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale