13/12/16

QUIZ: la vendetta di Quazel **

Categorie: Fisica classica Tags: densità quiz rotazione Scritto da: Vincenzo Zappalà Commenti:34

Quazel è un alieno simpatico e paziente... ma il putiferio che ha fatto nascere e la poca considerazione che ha ricevuto, all'inizio, lo spinge a rivolgere anch'egli una domanda ai terrestri.

La domanda è molto semplice:

"Il mio pianeta è molto speciale, ve lo assicuro. Tuttavia non dovreste avere difficoltà a dirmi qual è la sua densità minima, dicendovi che ruota in 6 dei vostri minuti".

Forza, sapientoni terrestri... rispondete al nostro Quazel!

34 commenti

Daniela

13/12/2016 at 11:26

Intanto, sarebbe opportuno che il simpatico Quazel, visto che è così portato per l'apprendimento del linguaggio, evitasse un errore di grammatica cOsì grossolano... chissà QUAL E' ??
Vincenzo Zappalà

13/12/2016 at 11:36

poverino... lui è un matematico e non ha ancora imparato perfettamente il linguaggio terrestre, Voi sareste capaci di tradurre la domanda scritta così: "gthsvzooooksb thyrggt opsshr tipun?".

Ah, questi terrestri, sempre presuntuosi e egocentrici!!!!
Daniela

13/12/2016 at 11:44

Giusta osservazione! Infatti la colpa non è sua, ma di chi traduce dal quazeliano all'italiano...
Vincenzo Zappalà

13/12/2016 at 11:48

No, no, la domanda l'ha fatta proprio lui... con i suoi limiti... e io non mi sono sognato di correggerlo. Io sono molto accondiscendente e capisco i problemi degli alieni... Cos'è un apostrofo di fronte agli anni luce che ha dovuto percorrere????!!!! Terrestri, terrestri, si credono i padroni del Cosmo...
maurizio

13/12/2016 at 14:52

Veramente, dovrebbe trattarsi di un troncamento e non di un'elisione, credo proprio che si scriva qual è senza l'apostrofo....

Bravi traduttori.
Daniela

13/12/2016 at 14:54

Occhio, Maurizio... i traduttori hanno corretto il testo dopo la segnalazione
Pippo

13/12/2016 at 15:27

Tra il periodo di rotazione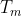 $T_m$ minimo e la densità 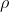$\rho$ del pianeta sussiste la relazione :

$T_m = \frac{1}{\sqrt{G\rho}}$

per periodi di rotazione inferiori , cioè per frequenze di rotazione maggiori , la materia comincia a sollevare dalla superficie .

Quindi deve essere :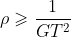 $\rho\geqslant \frac{1}{GT^2}$ , per la stabilità del pianeta .

$G$ è la solita costante di gravitazione universale .
Vincenzo Zappalà

13/12/2016 at 15:33

caro Pippo,

me la ricaveresti la relazione? E anche il valore finale, ovviamente... Deve servire per spiegare e ci vogliono tutti i passaggi...
maurizio

13/12/2016 at 15:34

Bravi e obbedienti...
Vincenzo Zappalà

13/12/2016 at 15:36

Comunuqe, l'esimio Prof. Dott. Lup. Mann. G.F. Mign. Ugo Lingualunga ha stabilito che elisione e troncamento sono la stessa cosa. Tra non molto insieme a Mauritius scriverà un saggio...
Pippo

13/12/2016 at 15:37

Caro Enzo,

ora te la spiega Maurizio .
Daniela

13/12/2016 at 15:40

Per quanto mi riguarda, l'unica Lingualingua a cui mi sembra opportuno dare credito è quella dell'Accademia della Crusca
Vincenzo Zappalà

13/12/2016 at 15:44

Lingualunga e non Lingualingua!!!

Accademia di che?

Crusca: Residuo della macinazione del grano, costituito da scagliette larghe e ben distinte;

La farina del diavolo va tutta in crusca, ciò che si ottiene con l'inganno o la frode non fa mai buon pro.

E io dovrei fidarmi di questa Accademia "diabolica" ??????????????????
Daniela

13/12/2016 at 15:49

E io che pensavo di avere a che fare con persone serie...

(comunque volevo scrivere Lingualunga, ma quando si fanno tre cose contemporaneamente, capita di sbagliare )
Vincenzo Zappalà

13/12/2016 at 15:52

Non conoscere i grandi pensatori e linguisti moderni... che triste mondo il nostro...

Va bene, facciamo le persone serie e pensiamo a risolvere il quiz...
Vincenzo Zappalà

13/12/2016 at 17:34

cari amici,

non spaventatevi dalle nostre farneticazione... sapete che adoriamo pensare divertendoci e divertirci pensando. La formula risolutiva è molto facile da trovare ed è alla portata di tutti coloro che conoscono le basi più basi della meccanica. Basta ricordarsi la velocità di fuga e il fatto che vogliamo che il pianeta non si ... sgretoli.

Forza, qualche silenzioso si faccia avanti! Giuro che non gli aizziamo contro nessuna volpe. Qualsiasi sia il risultato trovato, sbagliato o giusto, è sempre un enorme passo avanti nella conoscenza dell'Universo!
gianni bolzonella

13/12/2016 at 20:36

La logica vi porterà da A a B,l'immaginazione dappertutto.

A E.
Pippo

13/12/2016 at 23:23

Un oggetto di massa $m$ , poggiato a terra all'equatore di un corpo celeste in rotazione , rimane a terra e non se ne distacca se la forza apparente centrifuga è minore, in modulo, (o al più uguale) alla forza di attrazione gravitazionale che il corpo celeste esercita si di esso :

$m\frac{v^2}{R}\leq G\frac{Mm}{R^2}$

semplifichiamo la massa dell'oggetto, per cui deve essere :

$\frac{v^2}{R}\leq G\frac{M}{R^2}$

quindi la velocità periferica all'equatore deve essere minore della prima velocità cosmica :

$v\leq \sqrt{\frac{GM}{R}}$

per la Terra , la prima velocità cosmica vale circa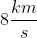 $8 \frac{km}{s}$ .

LA velocità periferica è data da :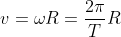 $v = \omega R = \frac{2\pi }{T}R$

dove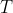 $T$ è il periodo di rotazione , cioè il tempo impiegato a compiere un giro completo.

D' altronde la massa M del corpo celeste, supposto sferico, si può scrivere come :
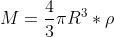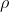$M= \frac{4}{3}\pi R^3*\rho$ dove $\rho$ è la densità media , supposta uniforme .

Quindi , elevando al quadrato la (1) e sostituendo le grandezze dette , deve essere :

$(2\pi\frac{R}{T})^2 \leq G *\frac{4}{3}\pi R^3 *\rho*\frac{1}{R}$

elevando al quadrato il primo membro, e semplificando quello che c'è da semplificare , risulta infine che deve essere verificata la seguente condizione :

$\frac{3\pi}{T^2}\leqslant G\rho$

e quindi il periodo rotazione deve essere :

$T \geq \frac{3.07}{\sqrt{G\rho}}$

(Nel primo messaggio mi ero scordato di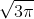 $\sqrt{3\pi}$ al numeratore . )

I valori numerici però non li metto.
Pippo

14/12/2016 at 05:04

Aggiungo che se è assegnato il periodo T espresso in secondi , essendo nota la costante di gravitazione universale:

la densità del corpo celeste deve soddisfare la condizione :

$\rho \geqslant \frac{3\pi}{GT^2}$

in cui T è appunto il periodo di rotazione dato, in secondi . Il risultato è in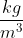 $\frac{kg}{m^3}$ .

Per T = 6 min = 360 s , risulta :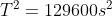 $T^2 = 129600 s^2$ , e quindi deve essere :

$\rho \geqslant 1090285 \frac{kg}{m^3} \simeq 1.09*10^6\frac{kg}{m^3}$

Ma da dove viene questo Alieno ......
Vincenzo Zappalà

14/12/2016 at 06:37

se no che alieno sarebbe ???
Pippo

14/12/2016 at 07:20

La densità media della Terra è 5514 kg/m^3 (pari a 5.5 g/cm^3 circa)

la densità del pianeta alieno è 197.73 volte (almeno) maggiore.

Si può sapere il raggio di questo pianeta del Quazel?
Vincenzo Zappalà

14/12/2016 at 08:03

Temo che questo non ce lo dirà mai... sai ogni alieno ha un suo segreto. Di sicuro è meglio non cercare di sollevarlo...

Aspettiamo che arrivi qualche altra risposta... magari utilizzando metodi ... alieni...
Arturo Lorenzo

14/12/2016 at 09:17

"Basta ricordarsi la velocità di fuga e il fatto che vogliamo che il pianeta non si ... sgretoli."

Deduco, quindi, che qui si vuole evitare che la materia posta in superficie sul pianeta non sfugga al suo campo gravitazionale. Direi, allora, che la velocità cosmica da considerare sia la seconda, cioè quella di fuga. In pratica, in questa situazione, mettendomi in un sistema di riferimento esterno al pianeta, credo sia lecito pensare che l'energia cinetica posseduta da un pezzo di materia posta sulla superficie del pianeta (dovuta alla velocità tangenziale v con cui il pezzo di materia vi muove per effetto della rotazione del pianeta) eguaglia la sua energia potenziale (calcolata con riferimento al centro del pianeta stesso):

$\frac{1}{2}mv^{2}=mgR$

Semplificando m e ricordando che

$g=\frac{GM}{R^{2}}$ (dove M è la massa del pianeta ed R il suo raggio)

ottengo:

$\frac{1}{2}v^{2}=\frac{GM}{R}$ (da questa relazione si ricaverebbe subito la velocità di fuga caratteristica per quel pianeta..)

Ora, v è legata alla velocità di rotazione del pianeta attraverso la relazione:

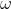$v=\omega R$

Inoltre, $\omega$ è legata al periodo di rotazione T attraverso la relazione:

$\omega = \frac{2\pi }{T}$

Infine, la massa M è legata alla densità del pianeta attraverso la relazione:

$M=\rho V = \rho \frac{4}{3}\pi R^{3}$ (dove V è il volume di una sfera di raggio R)

Quindi la (1) diventa:

$\frac{1}{2}\frac{4\pi ^{2}}{T^{2}} R^{2}=\frac{G\rho \frac{4}{3}\pi R^{3}}{R}$

da cui, dopo qualche passaggio si trova:

$\rho =\frac{3\pi }{2GT^{2}}$

La densità del pianeta, perché la materia non sfugga via dalla sua superficie (all'equatore) , dovrà dunque essere maggiore del valore sopra ricavato.

In pratica, se tanto mi dà tanto, potrei anche avere materia che galleggia in superficie, ma che non sfugge al campo gravitazionale del pianeta, quindi quest'ultimo non si sgretola. Sempre se ho capito bene il concetto di sgretolarsi e se i conti sono giusti
Vincenzo Zappalà

14/12/2016 at 09:35

mi sembra interessante la differenza dell'approccio: tutto sta a decidere se basta fare smuovere un qualcosa o mandarla all'infinito. E, quindi, il fattore 2. Una bella occasione per parlare di velocità cosmica... Perché non vi mettete insieme (tu e Pippo) e fate una piccola spiegazione per poi passare ai calcoli. Un richiamo al campo gravitazionale, all'energia, ecc., ecc.

Purtroppo, come al solito, siete sempre gli stessi... ma temo che non ci sia niente da fare con i silenziosi...

Dai, lascio a voi la soluzione!!!!
Pippo

14/12/2016 at 13:37

Vincenzo dice :

Temo che questo ( il raggio del pianeta Q ) non ce lo dirà mai... sai ogni alieno ha un suo segreto. Di sicuro è meglio non cercare di sollevarlo...

E perchè ? Magari l'accelerazione di gravità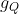 $g_Q$ sul pianeta di Quazel è maggiore di quella sulla Terra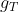 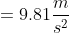$g_T$ $= 9.81 \frac{m}{s^2}$ ( al suolo) , e quindi Quazel sulla Terra pesa di meno che sul suo pianeta. Si ha :

$g_Q = G \frac{M_Q}{R_Q^2 }$

$g_T = G \frac{M_T}{R_T^2 }$

e quindi , se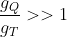 $\frac{g_Q}{g_T} >> 1$ , l'alieno, che ha la sua massa, sulla Terra pesa pochissimo ! Questa condizione , in termini di densità e raggi, si può scrivere :

$\frac{4}{3}\pi*R_Q^3*\rho_Q* \frac{1}{R_Q^2} >>\frac{4}{3}\pi*R_T^3*\rho_T* \frac{1}{R_T^2}$

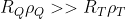
ovvero : $R_Q\rho_Q >> R_T\rho_T$

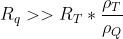e quindi : $R_q >> R_T * \frac{\rho_T}{\rho_Q}$ , cioè ancora : 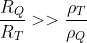$\frac{R_Q}{R_T} >> \frac{\rho_T}{\rho_Q}$ ( se i due rapporti fossero uguali, il rapporto tra i raggi sarebbe uguale all'inverso del rapporto tra le densità ) .

Ecco perchè avevo chiesto il raggio del pianeta Q !

Arturo ,

non capisco perchè vuoi proprio mandare all'infinito un oggetto di massa m , posto sulla Terra che ruota in modo che la velocita periferica sia uguale alla velocità di fuga ! Per me , anziché la velocità di fuga, detta anche la seconda velocità cosmica , che per la Terra vale circa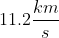 $11.2 \frac{km}{s}$ , ed è data da 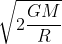$\sqrt{2\frac{GM}{R}}$ , è sufficiente la prima velocità cosmica, data da : 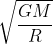$\sqrt{\frac{GM}{R}}$ . LA prima velocità cosmica corrisponde all'orbita circolare C di questa figura:

Pensa alla Terra , ricoperta di acqua da cui emergono le terre . Basterebbe raggiungere la prima velocità cosmica all'equatore per ......prosciugare gli oceani, da Nord a Sud !
maurizio

14/12/2016 at 14:13

Insomma mille grammi per cm cubo... Un bel terreno compatto. Che vini ci saranno mai?

Approfitto per mettere a disposizione un po' di apostrofi, se a qualcuno possono servire da mettere qua e là, secondo i gusti... ''''''''''''''''''''''
Vincenzo Zappalà

14/12/2016 at 15:34

caro Pippo, lasciamo da parte il peso se no finiamo con un quiz che non finisce mai come quello della volpe.

Uguagliare forza centrifuga e forza centripeta era cosa adatta a tutti e quindi la soluzione era anche nelle capacità dei meno preparati. Ci mancherebbe altro che uno come te non conoscesse queste formulette banali... L'idea di pensare a buttare proprio via la massa e non farla ricadere perché sbatte contro qualche montagna o per attrito atmosferico poteva essere usata per richiamare la velocità di fuga. Comunque, hai risposto esattamente in via puramente teorica... Possiamo anche concludere il quiz. Ringrazio anche Arturo per averla richiamata...

Per un po' non inserirò più quiz... e lascerò il compito al club dei maghi
Vincenzo Zappalà

14/12/2016 at 16:15

Ah... dimenticavo:

la risposta giusta è esattamente quella di Pippo e non c'è motivo di rispondere in alto modo. Possiamo considerare chiuso il quiz.

grazie a tutti!
Paolo

14/12/2016 at 16:54

Caro Enzo, stavo aspettando i tre giorni dedicati ai silenti, ma vedo che ormai le danze sono belle che iniziate… e finite...

Provo a proporre due diverse soluzioni, giusto per esercitarsi un pò, una improntata sulla velocità di fuga, l’altra sulla velocità orbitale.

Per trovare la velocità di fuga è necessario ragionare sulla conservazione dell'Energia.

Un oggetto che parte con una certa velocità dalla superficie di un pianeta, all'inizio ha:

E (cinetica) = ½ mv²

E (potenziale) = - GMm/r

E (totale) = E (cinetica) + E (potenziale) = ½ mv² - GMm/r

Per sfuggire completamente e per sempre alla gravità del pianeta, l'Energia cinetica dell'oggetto deve esaurirsi quando la sua distanza dal pianeta si avvicina a infinito (Ec= 0, mentre la negativa Energia di potenziale continua a crescere fino ad avvicinarsi a zero (Ep = 0, l'Energia di potenziale parte da valori negativi, per cui più si avvicina a zero e più cresce).

Quindi in quell'ipotetico momento l'Energia Totale diventa uguale a zero:

Etot = Ec + Ep = 0 + 0 = 0

Considerato che l'Energia totale deve conservarsi (non ci sono altre forze in campo se non la gravità del pianeta e la velocità dell'oggetto), questa doveva essere tale anche quando questo è partito, ossia:

Etot = Ec + Ep = ½ mv² - GMm/r = 0

Per trovare il valore della velocità che consente all'oggetto di sfuggire definitivamente (per sempre) alla gravità del pianeta (velocità di fuga), basta partire dall'equazione precedente:

½ mVf² - GMm/r = 0

½ mVf² = GMm/r

½ Vf² = GM/r

Vf² = 2GM/r

Vf = √2GM/r

Ciò significa che se il pianeta di Quazel ha una velocità di rotazione maggiore di Vf, è destinato a disgregarsi e disperdersi irrimediabilmente nello spazio, poiché tutto sfugge irrimediabilmente dalla sua superficie.

La velocità con cui un qualunque granello della superficie del pianeta compie un giro completo, una circonferenza, (moto circolare uniforme) è data da:

V = Circonferenza/periodo di rotazione = (2 π r)/T

dove T è il periodo di rotazione di Quazel

Quindi affinché il pianeta non si disgreghi tale velocità deve essere inferiore a quella di fuga, ossia:

V < Vf

Non resta che ricordare che la Massa M del pianeta che compare nella formula della velocità di fuga, è uguale alla densità moltiplicata per il volume occupato dal pianeta:

M = densità x Volume = ρ Volume

Ma il volume di una sfera (si presume che Quazel sia sferico) è uguale a:

Volume sfera = 4/3 π r³ quindi, la sua Massa può essere espressa:

M = (ρ π r³) 4/3

Considerato che:

Vf² = 2GM/r

Vf² = (2G (ρ π r³)4/3)/r = 8G ρ π r²/3

Elevando al quadrato la Velocità di rotazione di Quazel, è possibile confrontare le due velocità e verificare che V sia minore della velocità di fuga:

V = (2 π r)/T

V² = (4 π² r²)/T²

Per evitare la disgregazione del pianeta, deve perciò valere che:

V² < Vf²

4 π² r²/T² < 8G ρ π r²/3

4 π /T² < 8G ρ/3

12 π /8G T² < ρ

3 π /2G T² < ρ

ρ > 3 π /2G T²

Per trovare il valore della densità minima che deve avere Quazel per non disgregarsi, basta inserire i valori di G (6,67 × 10^−11 m³/Kg s²) e T (6 minuti, ossia 360 secondi).

ρ > 3 π /2G T² > 545 142 Kg/m³

Se non ho sbagliato qualche calcolo ne esce un pianeta ultra denso, ben più della Terra (circa 5 500 Kg/m³).

La seconda possibile soluzione, prende invece in considerazione la velocità orbitale, ossia quella specifica velocità che controbilancia perfettamente l’accelerazione di gravità, perciò ciò che sta al suolo non deve avere sufficiente velocità per allontanarsi da esso.

Tale equilibrio si ottiene considerando che, l’accelerazione centripeta è uguale a:

ac= V²/r

e che tale accelerazione è quella dovuta alla forza di gravità, ossia partendo da F= m a:

a = F/m = G m M/m r²= G M/r²

Basta eguagliare queste due relazioni, per ottenere la velocità (Vo velocità orbitale):

Vo ²/r = G M/r²

Vo ² = G M/r

Vo = √G M/r

Anche in questo caso la velocità di rotazione del pianeta deve essere inferiore a quella appena trovata, ossia:

V < Vo

Come prima conviene confrontare tali velocità elevate al quadrato:

V² < Vo²

(4 π² r²)/T² < G M/r

Sostituendo alla massa densità e volume:

4 π² r²/T² < (G (ρ π r³)4/3)/r

4 π² r²/T² < 4 G ρ π r²/3

π/T² < G ρ/3

3π/ G T² <ρ

ρ > 3 π /G T²

In questo caso per trovare il valore della densità minima che deve avere Quazel, basta inserire i valori di G (6,67 × 10^−11 m³/Kg s²) e T (6 minuti, ossia 360 secondi)

ρ > 3 π /2G T² > 1 090 285 Kg/m³

Sempre che non abbia sbagliato qualche calcolo...

Paolo
Vincenzo Zappalà

14/12/2016 at 17:24

grande Paolo! hai proprio espresso la situazione nei due modi possibili e in modo perfettamente divulgativo. Le conclusioni sono, perciò, quelle di Pippo e Arturo..

Carissimo, bentornato... sentivamo la tua mancanza!!! Quando si impara in prima persona con tanta umiltà si diventa automaticamente ottimo divulgatore
leandro

14/12/2016 at 22:08

Beh così è troppo facile. Ma come si comporta un elemento di materia che non sta sull'equatore? siete così sicuri che rimanga ben ancorato al pianeta? eh eh eh :-)
Paolo

14/12/2016 at 23:15

Scusa Leandro, forse non ho compreso bene cosa intendi.

A me sembra che in entrambi i casi proposti il presupposto è che la velocità di rotazione (intesa come velocità tangenziale) deve essere minore o della velocità orbitale o di quella di fuga.

La velocità di rotazione V raggiunge il suo massimo all'equatore, fino a ridursi a zero ai poli.

Infatti: V= 2 π r/T

dove r è la distanza tra un granello della superficie e il centro di rotazione (asse di rotazione).

All'equatore tale distanza raggiunge il suo massimo, per cui nel medesimo periodo T di rotazione viene percorsa una circonferenza maggiore rispetto ad un granello che si trova più distante dall'equatore.

Man mano che ci si avvicina ai poli la distanza tra la superficie e l'asse di rotazione diminuisce (r minore) per cui si riduce anche la velocità di rotazione V (nel medesimo periodo T di rotazione viene percorsa una circonferenza minore).

Quindi se anche laddove la velocità di rotazione è massima, ossia all'equatore, è comunque inferiore a quella orbitale o a quella di fuga, avvicinandosi ai poli tale divario aumento a favore della velocità orbitale o di quella di fuga.... quindi un oggetto sarebbe ancora più ancorato al terreno...

Sbaglio?

Paolo
Pippo

15/12/2016 at 00:23

Leandro dice :

Beh così è troppo facile. Ma come si comporta un elemento di materia che non sta sull'equatore? siete così sicuri che rimanga ben ancorato al pianeta? eh eh eh :-)

se hai letto fino in fondo il mio post , ho detto che raggiungere la prima velocità cosmica sull'equatore avrebbe come conseguenza ....un po' catastrofica direi.... di prosciugare gli oceani da Nord a Sud

Un motivo deve pur esserci !
Vincenzo Zappalà

15/12/2016 at 06:23

hai ragione Paolo. Se scappa qualcosa scappa di lì. A parte il fatto che la materia tende a scendere verso l'equatore (ne avevamo parlato a lungo alla fine del momento angolare, ricordi...). Se il momento angolare è sufficiente si può anche avere la scissione in due corpi dominati dall'autogravitazione soltanto, proprio come capita negli asteroidi che sono mucchi di sassi...

Comunque, ancora una volta i silenziosi hanno il dito che scotta e non osano scrivere niente... peccato...

Non capisco se hanno bisogno di più tempo o hanno troppa paura a provare. Non so se metterò altri quiz che servano solo a 4 o 5 persone. Al limite, ce li passiamo tra di noi...

Il mondo, forse, si divide proprio in due parti: chi ha paura di apparire e chi invece lo vuole fare a tutti i costi. Coloro che non sono sicuri ma ci provano lo stesso, sapendo che non saranno mai fustigati in pubblico, stanno scomparendo del tutto... E pensare che proprio discutendo degli errori si riesce a comprendere meglio le cose. caro Paolo, il mondo è quello che è e ce lo dobbiamo tenere...

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.