Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

 

L'immagine di copertina si capirà nel seguito. Per adesso, ci basti sapere che il numero 6 può essere sia GRANDE che PICCOLO... tutto dipende dai "sassolini" usati!

Per parlare dei numeri, non basterebbero tutti i libri esistenti al mondo. Essi non sono solo le lettere della matematica, ma molto, molto di più. La matematica (costruita da noi) usa i numeri, ma solitamente non s’interessa di cosa essi siano realmente e di come possano essere veramente descritti. Per capire meglio il loro mondo fantastico è necessario tornare all’antica Grecia (forse anche prima, ma i dati in nostro possesso sono troppo scarsi), in particolare alla scuola di Pitagora. Scopriremo un vero universo, pur limitandoci a poche nozioni. Scopriremo anche che la nostra tecnologia non è ancora riuscita a risolvere molti dei loro segreti. Chissà che un giorno i nostri Ciccio e Astericcio non decidano di fare un giro in questo mondo fantastico?!

Cosa sono i numeri?

A riguardo è molto indicativa la frase di Luca Pacioli, un religioso, economista e matematico del XV secolo, ma soprattutto un vero conoscitore dei numeri e della loro essenza:

“Ancora si comme fra la gente più imperfecti e tristi che buoni e perfecti si trovano e li buoni sono pochi e rari: così fra li numeri pochi e rari sono li perfecti e molti e assai sonno li imperfecti: cioè superflui e diminuiti”.

 Il mondo dei numeri è un mondo ben più complesso di quanto si pensi e non vi è nessun bisogno che essi siano veramente “complessi”, ossia facciano uso spudorato della radice quadrata di -1.  Il nostro modo di descriverli è veramente squallido e anonimo. Cosa direste infatti se, all’atto della vostra nascita, vi fosse stato affibbiato solo un codice più o meno numerico, del tipo PX112CF? Appena in grado di farlo, urlereste: “Non sono mica una targa di automobile o una bottiglia o una merce qualsiasi? Sono una donna/uomo, merito molto di più. Sono un essere vivente, con la mia personalità, le mie idee, le mie speranze, i miei desideri, i miei difetti. Un numero, ma siete matti?”

Ebbene, le stesse considerazioni valgono per i … numeri. Anche loro sembrano nascere nell’atto in cui li scrivete o li pronunciate. Un esempio? “234167432”. Cosa ho fatto? Ho scritto un numero qualsiasi, un freddo anonimo numero? No, assolutamente no! Ho fatto nascere una creatura con tutte le sue caratteristiche che lo rende diverso da un altro, ne fa un esemplare unico!

Mi potreste dire: “Su, per favore, un numero nasce e muore a nostro piacimento, e poi ce ne sono tanti, infiniti… come poter credere che ognuno abbia una sua spiccata personalità?”

Mamma mia… non fatevi sentire da un elettrone o da un fotone… per cortesia. Anche loro sono praticamente infiniti e apparentemente tutti uguali tra loro, ma provate a chiamarli con un simbolo, un “numero” o un codice e sareste attaccati da una sequela di processi quantistici che vi distruggerebbero in un attimo. Loro sono buoni e cari, ma ricordate sempre che sono le uniche creature capaci di avvisarsi attraverso l’entanglement, un’informazione che fa apparire la luce una tartaruga, quasi imbarazzante nella sua lentezza.

Gli esempi sarebbero moltissimi e quindi fermiamoci pure: ne usciremmo sempre più sconfitti e appariremmo dei presuntuosi ignoranti. In fondo, lo sappiamo benissimo che non siamo noi a usare i numeri, ma sono loro che cercano di aiutare le nostre limitate potenzialità deduttive e interpretative attraverso ciò che noi chiamiamo matematica.  La matematica non è il mondo dei numeri, ma solo un linguaggio semplice che i numeri ci hanno concesso per avere solo una pallida idea del loro mondo.

Torniamo, perciò alla frase di Pacioli, uno che aveva capito molte cose, non per niente era amico di Leonardo da Vinci.

Come ci sono fotoni più o meno energetici così ci sono numeri più o meno importanti, potenti e conosciuti. Tuttavia, non pensiamo certo che mettere insieme le poche cifre che noi riteniamo fondamentali, da 0 a 9, sia capire l’essenza dei numeri. Nemmeno per sogno… quelle cifre le abbiamo create noi per riuscire a scriverli in qualche modo, ma loro esistono indipendentemente dalle nostre limitate capacità descrittive. Non è molto che abbiamo incontrato un alieno che usa cifre diverse per scrivere un numero. Non confondiamo quindi la cifra, un simbolo che abbiamo deciso noi, con un numero, un qualcosa di immutabile e unico.

Gli antichi greci l’avevano intuito e non per niente usavano figure geometriche per crearli, per farli giocare tra di loro, per accattivarseli e per cercare di carpirne qualche segreto. Poi, la modernità delle cifre ha sveltito i nostri squallidi calcoli e ci ha fatto credere di averli domati e di poterli trattare come oggetti senz’anima, adattabili ai nostri scopi intellettuali o scientifici.

Un po’ come capita alle parole che non sono certo un insieme di lettere, ma rappresentano qualcosa di ben più universale. Se scrivete “pane” vi riferite a qualcosa di specifico, di preciso, di reale. E, invece, se dite “quarantuno” pensate solo a quaranta volte uno e non a un’entità  che vive una sua vita indipendente e non certo banale.

C’è forse una vera differenza tra XLI romano e 41 arabo occidentalizzato?  E, allora, tanto vale mettere 41 sassolini uno a fianco dell’altro. Sareste decisamente più vicini alla realtà del mondo dei numeri. Così facevano i greci e probabilmente anche le civiltà più antiche, ben più vicine alla splendida realtà del Cosmo di quanto non lo siamo noi oggi schiavi dei calcolatori e di un’elettronica dominata dalle particelle quantistiche. Sono loro che si servono di noi per vivere le loro avventure e non certo il viceversa!

Torniamo a Pitagora e ai suoi seguaci. In particolare soffermiamoci su un nome molto difficile, ma di semplice comprensione: Aritmogeometria. Il suo significato non è altro che quello di rappresentare i numeri naturali (interi positivi) attraverso configurazioni geometriche di punti (o sassolini, se preferite).

Non cominciate, però, a dire che Pitagora era limitato, in quanto usava solo i numeri positivi… I numeri negativi non sono altro che uguali e opposti, ma difficilmente rappresentabili geometricamente.

Ridete di lui? Pensate all’antimateria e provate a costruirla in casa vostra, se ne siate capaci. Quanti vorrebbero costruire un’antisuocera e annichilire la propria suocera, ma nessuno c’è ancora riuscito! Bene, possiamo pensare che i numeri negativi siano gli antinumeri positivi. D’altra parte mettere quattro sassolini e poi toglierli subito, non è come annichilire un elettrone e un positrone? Il risultato è sempre zero e … non parlate di energia, dato che nessuno sa ancora misurare l’energia che deriva dai numeri e dalla loro annichilazione.

Ancora una volta, abbiamo visto l’estrema somiglianza tra i numeri e le particelle quantistiche. I veri padroni dell’Universo. Provate a costruire un presidente e un antipresidente. Faranno di tutto per annichilirsi, ma mai riusciranno a sparire del tutto, anzi o ne sparisce uno solo o si metteranno d’accordo! L’essere umano è nettamente più limitato, non c’è dubbio…

Diceva Diogene di Laerzio riguardo ai pitagorici: “I numeri apparivano a loro primi tra tutto ciò che è nella natura; pensavano che gli elementi dei numeri fossero elementi di tutte le cose che sono, e che l’intero mondo fosse armonia e numero”.

Per non parlare di Aristotele: “I Pitagorici dicono che da numeri sono composte le sostanze percepibili. … Essi dicono che il numero è le cose che sono, o almeno applicano i loro teoremi ai corpi, come se i numeri fossero dei corpi”.

Alcuni esempi classici:

Il numero 1 rappresenta il principio di tutto, la ragione. In geometria è il punto o il sassolino.

Il numero 2 rappresenta la parte femminile, l’indefinito, l’opinione. In geometria è la linea.

Il numero 3 rappresenta la parte maschile, ciò che è definito e limitato. Geometricamente è il piano.

Il numero 4 è la giustizia, dato che può essere diviso con equità in due parti.

In numero 5 è il matrimonio (unione di 2 e 3)

Il numero 10 è la sintesi dell’Universo, dato che contiene l’inizio, la parte maschile, la parte femminile e la giustizia che lo domina. La sua rappresentazione geometrica è un triangolo equilatero di lato 4

Malgrado i dubbi e le velate prese in giro, i pitagorici riuscirono ad avere un colloquio diretto con i numeri e a sapere, almeno in piccola parte, il loro vero significato. Seppero che loro avevano gerarchie molto complicate e che vi erano numeri buoni, numeri cattivi, numeri timidi e numeri ambiziosi. Un mondo intricato e complesso, di cui ancora oggi conosciamo ben poco.

D’ora in poi useremo le nostre cifre per farci capire, ma ricordiamoci che stiamo usando solo sassolini e figure geometriche.

I numeri poligonali

Torniamo, quindi, a Pitagora e cerchiamo di conoscere i suoi numeri geometrici o, più esattamente, poligonali. Si potrebbe fare molto di più, ovviamente, ma dare a ogni numero una sua forma geometrica e un suo modo preciso e rigoroso di procreare e moltiplicarsi è già un passo in avanti verso la loro conoscenza…

Prendiamo un esempio banalissimo: i numeri triangolari (1, 3, 6, 10, …), che vediamo in Fig. 1.

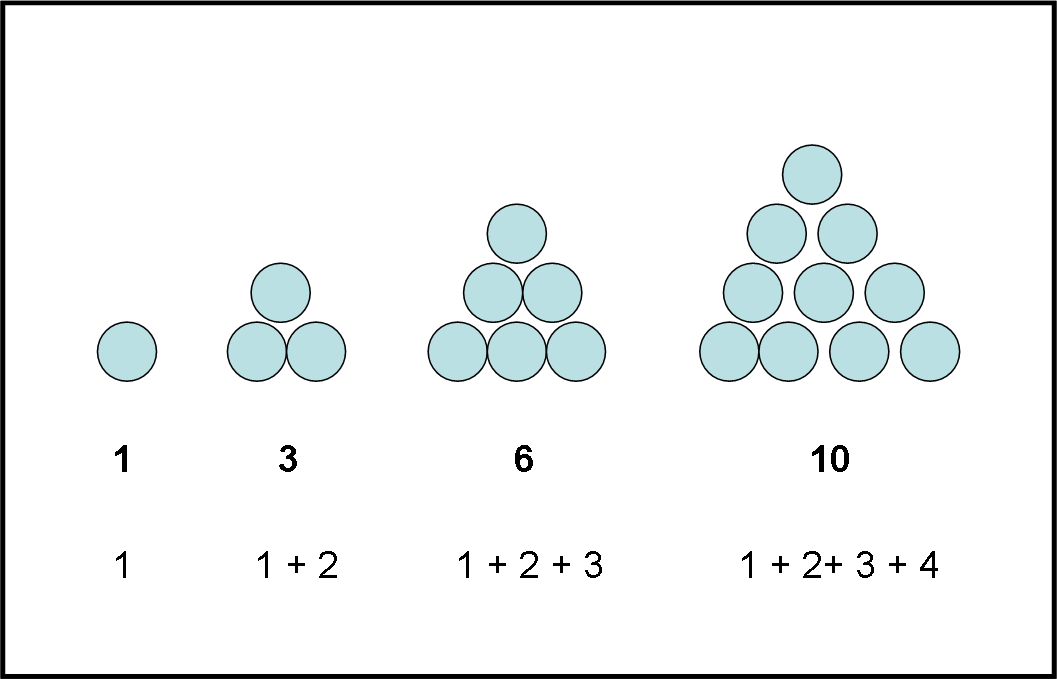
Numeri qualsiasi per noi, ma non certo per loro. Proviamo a sommare i numeri cominciando da 1.

1

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4= 10

 Lo schema vuole dire che il primo numero triangolare è 1, il secondo è 3, il terzo è 6, il quarto è 10, e via dicendo.

Ogni volta che aggiungiamo il numero intero successivo otteniamo un nuovo numero triangolare. Oggi diremmo che per ottenere un qualsiasi numero triangolare (l’ennesimo numero triangolare) basta sommare tutti i numeri fino al valore n cercato e scrivere:

Tn= 1 + 2 + 3 + 4 + …. +  n = n(n+1)/2   (serie di Gauss, ma vedremo che se ne può fare a meno)     …. (1)

In altre parole, molto più pratiche: per ottenere il decimo numero triangolare, basta sommare tutti i numeri da 1 a 10, ossia 1 + 2 + 3 + …. + 9  + 10 = 55

Così come abbiamo introdotto i numeri triangolari, possiamo andare avanti come hanno fatto i pitagorici. Ad esempio con i numeri quadrati. La loro descrizione è semplice (Fig. 2).

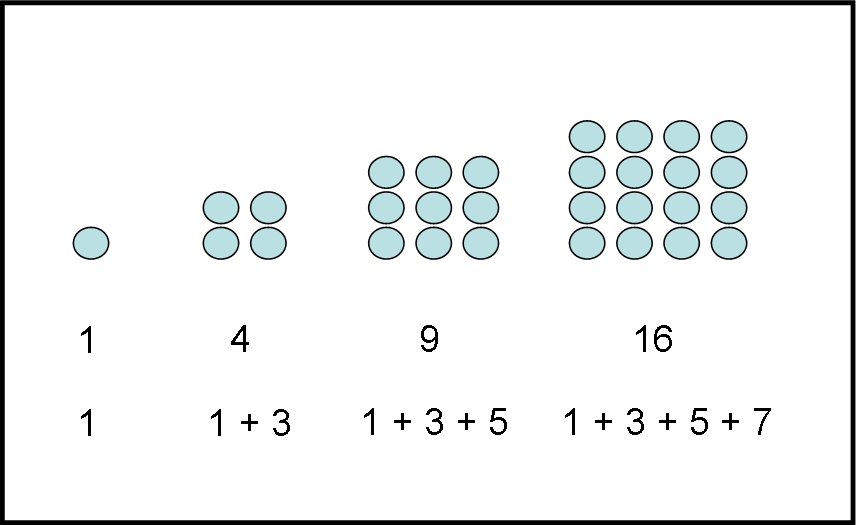
Essi sono:

1, 4, 9, 16, 25, …

Ovviamente sono tutti… quadrati di qualche numero, per costruzione. Il secondo è il quadrato di 2, il terzo è il quadrato di 3 e via dicendo.

Ma essi ci dicono cose molto importanti che li legano ai numeri triangolari e non solo..

Ad esempio, un numero quadrato è sempre uguale alla somma di un numero triangolare e di quello successivo. La faccenda si nota immediatamente dalla Fig. 3, dove i numeri triangolari consecutivi sono identificati con sassolini di colore diverso.

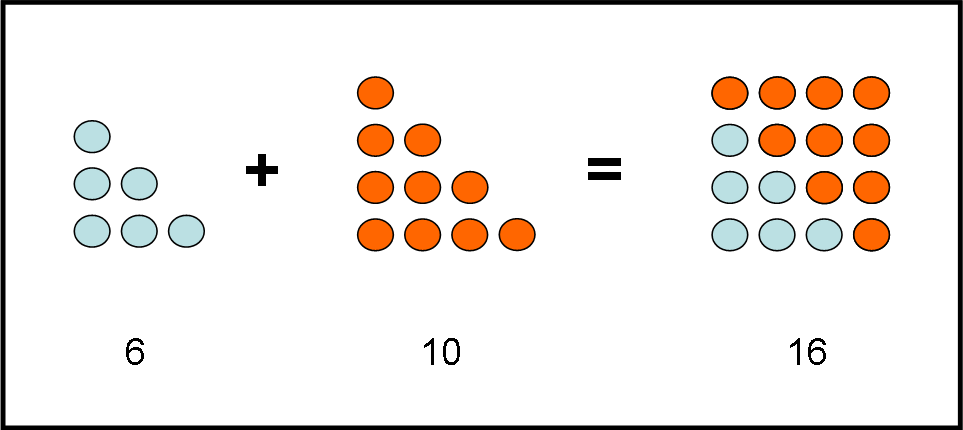
Se non crediamo alla figura, possiamo sempre usare le formule che ci siamo inventati in seguito:

il numero triangolare Tn è dato da:

Tn = 1 + 2 + 3 +… + n

Il numero triangolare T(n - 1) (quello precedente) è dato da:

T(n - 1) = 1 + 2 + 3 +… + (n - 1)

Ma la (1) ci dice anche che:

Tn = n (n + 1)/2

T(n-1) = (n - 1) n /2

Sommando:

Tn + T (n-1) = (n² + n + n² –n)/2 = n²

Bella forza! Ma niente di nuovo rispetto ai pitagorici… Sembra, infatti, che si sia dovuto usare una formula “moderna”. Nemmeno per sogno… la formula (1) si ricava facilmente usando la sola geometria. Lo vediamo in Fig. 4.

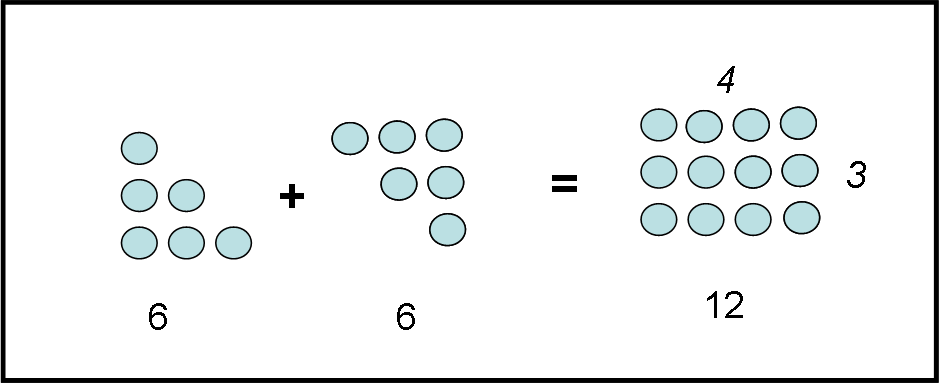
Prendiamo un numero triangolare Tn e gli accostiamo un altro numero triangolare Tn. La figura finale è un rettangolo di lati n e n+1, per cui deve contenere n (n + 1) punti (basta contare i sassolini). Ma questo numero è proprio il doppio dei numeri di un solo triangolo, ossia :

n(n+1) = 2Tn

da cui

Tn = n(n+1)/2

Con buona pace di Gauss…

Possiamo, però, svelare altri piccoli segreti, con i nostri sassolini, e avvicinarci anche alle prime misure astronomiche.

Prendiamo un bel numero quadrato e sottraiamogli il numero quadrato precedente (Fig. 5).

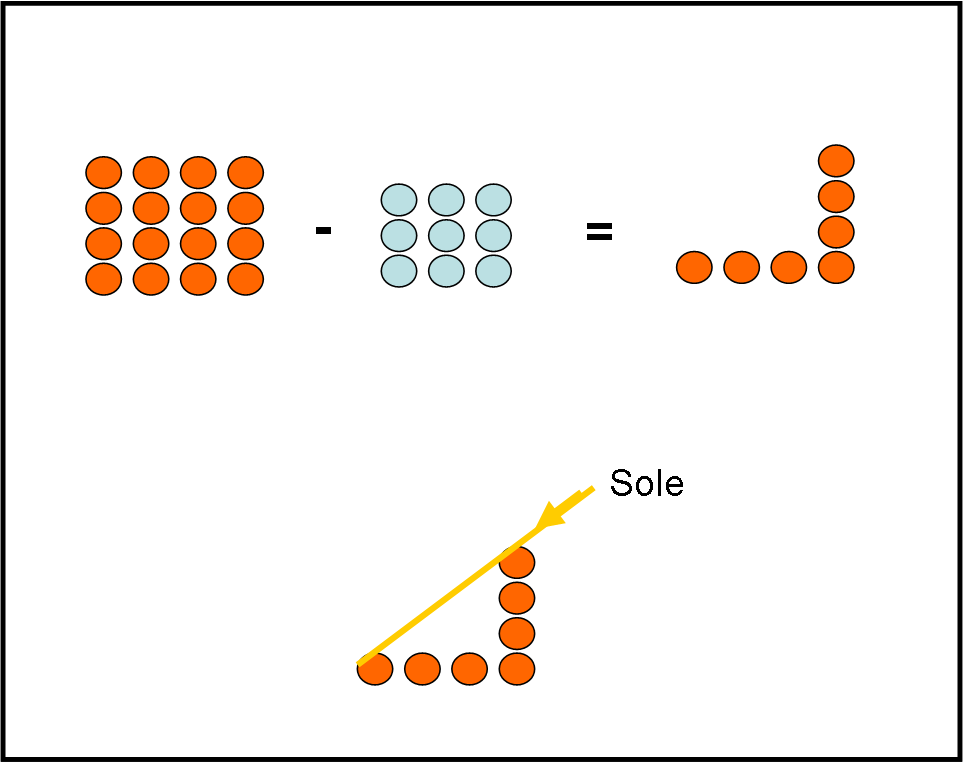
Cosa si ottiene? Una strana figura a L rovesciata orizzontalmente. Bene questa figura prende il nome di gnomone, ossia lo strumento base per tante misure, compresa quella della circonferenza della Terra (come fa è riuscito a fare Eratostene di Cirene nel III secolo a.C.). Essa simboleggia proprio un asta rigida con la sua ombra. Fantastico, veramente fantastico.

Vale anche il viceversa, ovviamente… Ossia, prendiamo il numero quadrato 4 (quattro sassolini). Aggiungiamogli lo gnomone relativo che è formato da 5 sassolini. Otteniamo il numero quadrato successivo, ossia 9. Abbiamo ripetuto quanto detto prima sottraendo da 9 il quadrato precedente, ossia 4, e ottenendo proprio 5, lo gnomone.

La faccenda si può scrivere in formule moderne, come:

(n + 1)² – n² =  n² + 1 + 2n – n² = 2n + 1     dove, nel caso precedente, n vale 2.

Infatti, il quadrato di due è proprio il numero quadrato 4, il quadrato di n + 1 = 3 è proprio il numero quadrato 9. Lo gnomone corrispondente è 2 ∙ 2 + 1 = 5.

In altre parole, abbiamo detto che per ottenere il numero quadrato successivo basta aggiungere lo gnomone corrispondente. Spieghiamoci meglio…

Prendiamo il primo numero quadrato, ossia 1. Aggiungiamo il suo gnomone che è  (2n + 1), ossia 2 ∙ 1 + 1 = 3 e otteniamo il secondo numero quadrato che è 4. Aggiungiamo a questo lo gnomone relativo che è 2n + 1 = 2 ∙ 2 + 1 = 5. Otteniamo il terzo numero quadrato 9. Prendiamo il suo gnomone che è 3 ∙ 2 + 1 = 7, lo sommiamo e otteniamo il quarto numero quadrato che è 16.

In parole molto povere, per ottenete il numero quadrato Qn basta sommare tutti i numeri dispari (ossia gli gnomoni). In parole “matematiche”:

Qn = 1 + 3 + 5 + 7 + 9 + … + (2n -1)        somma dei numeri dispari

Per ottenere il quarto (n =4), basta sommare 1 + 3 + 5 + 7 = 16    (7 è proprio 2n -1)

Per ottenere il quinto (n = 5), basta sommare 1 + 3 + 5 + 7 + 9 = 25    (9 è proprio 2n -1)

Insomma, gli gnomoni (i numeri dispari) servono sia a scrivere tutti i numeri quadrati, ma anche a misurare la circonferenza della Terra. Se non è una prova dell’importanza del mondo dei numeri questa…!

Ovviamente, i pitagorici sono andati avanti con i numeri poligonali, trovando relazioni sempre più complicate e generali, ma noi possiamo fermarci e prendere un’altra direzione, quella della perfezione. Per gli amanti dei numeri, però, abbiamo dato tanti spunti per entrare sempre più in questo mondo fantastico (e bastano solo dei sassolini o, se preferite, dei punti disegnati su un foglio). Provate con i pentagoni, gli esagoni e potrete scoprire proprietà fantastiche.

Non tutti sono perfetti

Costruendo un numero in forma geometrica non è difficile ottenere facilmente i suoi divisori, ossia i numeri che sono contenuti, nel numero in questione, un numero intero di volte. Un legame molto profondo e reciproco. Prendiamo il numero 8. Esso può essere ottenuto prendendo il due quattro volte oppure prendendo il quattro due volte. Ovviamente, 1 è un divisore di tutti i numeri, così come lo stesso numero. Quest’ultimo però non viene considerato come divisore, nella ricerca del carattere profondo dei numeri.

I divisori diventano molto importanti sommandoli tra di loro. Proviamo con quelli di 8 (1, 2, 4) …

1 + 2 + 4 = 7

Proviamo con quelli di 10 (1, 2, 5) …

1 + 2 + 5 = 8

Cosa ci dicono questi risultati? I numeri 8 e 10 sono numeri difettivi, ossia sono quelli del tipo “vorrei, ma non posso”. Fanno di tutto affinché la somma dei loro divisori sia uguale proprio al numero, ma non ci riescono, a volte per pochissimo. Sono numeri un po’ tristi, a cui manca qualcosa per raggiungere un posto di rilievo.

Proviamo con il numero 12

1 + 2 + 3 + 4 + 6 = 16

Accidenti… quanta arroganza! E’ del tipo “meglio esagerare sempre”. Sono numeri per cui la somma dei divisori è maggiore del numero e si chiamano eccedenti o abbondanti. Personaggi di cui fidarsi poco, troppo ambiziosi e pericolosi.

Pensate che Nicodoco (vissuto nel I secolo dopo Cristo) ne dà una descrizione ben più severa: i numeri difettivi sono creature malate, infelici, prive di qualche parte importante, come un cane cieco. I numeri eccedenti, invece, abusano degli altri, sono violenti, come mostri con molte file di denti.

Che siano veramente privi di regole lo dimostra un fatto piuttosto interessante. Esistono moltissimi numeri leggermente difettivi, ossia i cui divisori, se sommati, hanno solo un’unità di differenza dal numero, proprio come il numero 8, i cui divisori arrivano solo fino a 7. Invece, non esistono numeri lievemente eccedenti, ossia per cui la somma dei divisori sia solo di un’unità maggiore del numero.

Fermiamoci un attimo. L’ultima asserzione è del tutto ipotetica: ad oggi non è ancora stato trovato, malgrado i computer, un numero lievemente eccedenti, ma non vi è niente che dimostri che non possa esistere! Il mondo “reale” dei numeri è ancora pieno di misteri, non ancora svelati.

La prossima volta affronteremo il meglio del meglio, i numeri perfetti.

 

QUI potete trovare tutti gli articoli sull'Universo dei Numeri