Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Cari amici, volevo proseguire con i numeri perfetti (QUI) e la loro lunga storia… quando mi sono accorto (e qui c’è molto di soggettivo, ovviamente) che l’Universo dei Numeri può essere decisamente più complesso di quello che siamo abituati a guardare con il telescopio o ipotizzare con le formule… Probabilmente unisce in lui (o in loro?) sia i fenomeni più classici della meccanica quantistica che una struttura multi dimensionale, rispetto alla quale noi siamo decisamente più indietro.

Voglio scrivere una provocazione: quando conosceremo molto meglio il mondo dei numeri, proseguendo lungo le linee aperte dai grandi scienziati antichi, forse capiremo molto di più del vero spaziotempo in cui viviamo. Calco ancora più la mano: l’applicazione degli schemi matematici, attraverso formule sintetiche, potrebbe avere interrotto la strada più rapida verso la conoscenza TOTALE.

Non ridete, ma non prendetemi nemmeno troppo sul serio … certi pensieri e certe riflessioni devono essere discusse e confrontate. Quindi, prima di gettare al macero queste idee così “vagabonde” proviamo, tutti assieme, di ragionarci sopra. Al limite ci saremo divertiti un po’…

Vorrei, innanzitutto, arrivare a una visione quantistica dell’Universo dei numeri “figurati”, ossia quelli poligonali, formati da tanti sassolini o tanti punti o -ancora- da tante particelle minutissime. Non voglio nemmeno toccare la disposizione atomica nelle molecole o cose del genere che ci porterebbero nel mondo della chimica, in cui i numeri figurati la fanno sicuramente da padroni. No, mi basta restare alla definizione dei numeri poligonali e poco di più. Sveleremo mondi sconosciuti e, al momento, inavvicinabili.

Scriviamo i nostri numeri interi positivi uno dietro l’altro, ricordando che usiamo le cifre solo per facilità di scrittura: in realtà stiamo mettendo sassolini vicini tra loro.

Ora divertiamoci a sommare i numeri, come abbiamo fatto la volta scorsa:

1

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4 = 10

Possiamo fare la stessa cosa, ricordandoci di volta in vola la somma precedente:

1

1 + 2 = 3

3 + 3 = 6

6 + 4 = 10

Otteniamo, ovviamente lo stesso risultato…. Tuttavia, questo secondo “metodo” ci permette di rappresentare l’operazione svolta attraverso la Fig. 1a.

Partiamo dalla prima riga dove ci sono tutti i numeri naturali. Riportiamo nella riga sotto il numero 1, l’origine di tutto, il numero che comanda tutti gli altri, la particella unitaria, il niente e il tutto, (il Big Bang…?).

Iniziamo a costruire, nella seconda riga, gli attori del “primo” Universo… sommiamo il primo numero della seconda riga (1) con il secondo della prima riga, ossia 1 + 2 = 3. Il risultato lo scriviamo come secondo numero della seconda riga. Prendiamo questo numero e sommiamolo con quello successivo della prima riga: 3 + 3 = 6. Scriviamolo e andiamo avanti con le somme e con la costruzione della seconda riga.

Beh… quello che abbiamo fatto è semplicissimo: abbiamo costruito la serie dei numeri TRIANGOLARI. Niente di nuovo, ovviamente. Tuttavia, possiamo considerare questi numeri -o agglomerati di particelle- gli attori di un particolare Universo in cui i personaggi si fanno via via più complessi pur seguendo sempre la stessa legge. Permettetemi di chiamarlo Universo Numerico Triangolare (UNT). I suoi abitanti hanno una caratteristica comune, quella di formare SEMPRE un triangolo equilatero.

Ricominciamo dall’inizio con la serie dei numeri… (Fig. 1b). Questa volta, però, ne cancelliamo uno no e uno sì. Ossia cancelliamo il 2, il 4, il 6, l’8, ecc. In poche parole, consideriamo i numeri dispari.

Seguiamo la legge operativa precedente. Sommiamo il primo numero (1) della seconda riga con il primo numero NON cancellato della prima riga (il 3). Abbiamo 1 + 3 = 4. Riportiamolo nella seconda riga . Prendiamo proprio lui e sommiamolo al numero successivo della prima linea (non cancellato, ovviamente). Abbiamo 4 + 5 (il 4 della prima riga è stato cancellato) = 9. Riportiamolo nella seconda riga e andiamo avanti con l’operazione che ormai conosciamo molto bene. Cosa otteniamo? Beh… lo sappiamo già dalla volta scorsa: i numeri QUADRATI. L’altra volta li avevamo trovati sommando i numeri dispari e, infatti, abbiamo operato in modo del tutto simile. Possiamo dire di avere costruito un secondo Universo, quello quadrato, l’Universo Numerico Quadrato (UNQ).

No, non ridete ancora… So benissimo che basterebbe fare una moltiplicazione o utilizzare un simbolo matematico. Lasciatemi proseguire in questo gioco da fanciulli, in cui sappiamo solo aggiungere sassolini…

Riprendiamo la solita serie dei numeri (Fig. 1c) e, dopo l’1, cancelliamo due numeri consecutivi. Nella seconda riga si mette sempre l’1 e poi lo si somma con il primo numero non cancellato, che questa volta è il 4. La somma è 5 e possiamo riportarlo nella seconda riga. Prendiamo il 5 e lo sommiamo con il successivo numero non cancellato, che è il 7. Otteniamo 12. Andando avanti troviamo il 22 e via dicendo.

Bene la serie 1, 5, 12, 22 non è altro che un nuovo Universo. Stiamo solo attenti a NON RIEMPIRE la figura ottenuta (il pentagono) e costruiamo il pentagono successivo, prolungando i lati di quello precedente. La figura illustra bene l’operazione. Non ho nemmeno bisogno di dirlo… ma abbiamo costruito l’Universo Numerico Pentagonale (UNP).

Passiamo alla Fig. 2 (ormai avete capito il procedimento), dove abbiamo cancellato tre numeri consecutivi.

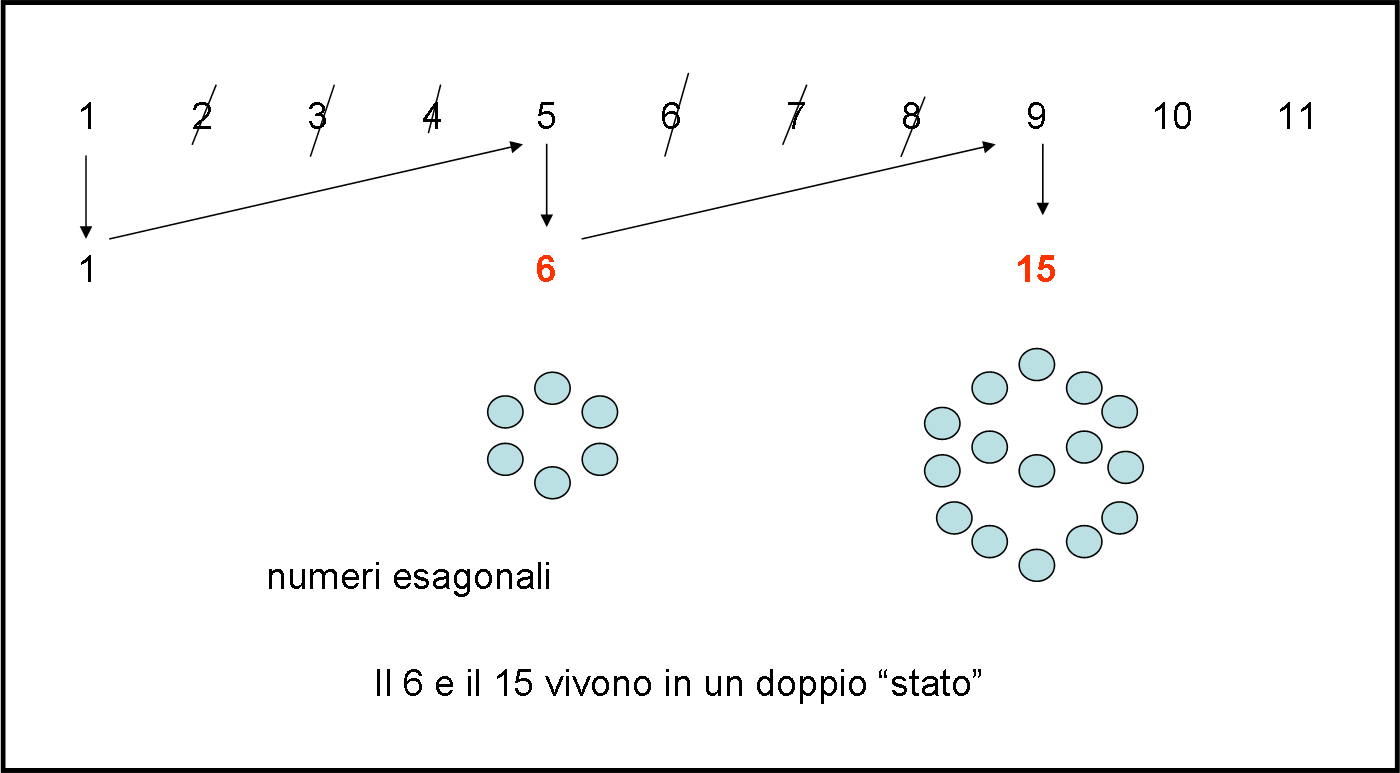
Ripetiamo la solita trafila 1 + 5 = 6; 6 + 9 = 15; ecc., ecc. I sassolini che si vedono sotto ai numeri della seconda riga la dicono lunga: sono esagoni, costruiti sempre prolungando i lati e senza riempire tutta la figura. Bene, potete dirlo da soli, abbiamo in mano l’Universo Numerico Esagonale (UNE).

Potremmo andare avanti all’infinito e avremmo infiniti Universi. Possiamo fermarci e riflettere. Tutti questi Universi sono sicuramente collegati tra loro, ma possono vivere indipendentemente. Le formule matematiche li legherebbero facilmente con cento strategie più o meno sofisticate. Ma a noi non interessa. Noi, per il momento almeno, abbiamo di fronte Universi paralleli (o quasi) in cui, però, certi numeri cominciano ad appartenere a più di un Universo. Ad esempio il 6 e il 15 e tutti quelli esagonali appartengono anche all’Universo triangolare. No, non ditemi: “Grazie… basta moltiplicare per due…” . Noi non siamo interessati alla moltiplicazione, operazione matematica che vogliamo far finta di non conoscere.

Bene.. posso permettermi di dire che il numero 6, il 15 e i loro compagni vivono in un doppio stato, ossia appartengono contemporaneamente a due Universi distinti. A seconda di come li raffiguro li faccio collassare in un Universo diverso.

Non fatemi proseguire con gli esempi… più andiamo avanti con la nostra operazione ripetitiva e più avremo numeri che appartengono a più stati e molte altre cose. Sì, sì, forse ho solo scherzato, ma quel numero 6 (che incontreremo ancora) ha acquistato un qualcosa di magico, così come quei sassolini o particelle che compongono i numeri a seconda dell’Universo in cui si possono sistemare.

Bisognerebbe studiare molto meglio i numeri figurati… quanto potrebbero insegnarci!

Fino a questo punto, però, abbiamo lavorato in un piano a due dimensioni (trascuriamo il volume dei sassolini) in cui compaiono tutti i poligoni che possiamo immaginare e che riusciamo a disegnare su un foglio. Tanti Universi bidimensionali…

Cerchiamo di andare un po’ più avanti e sfruttiamo un teorema enunciato dal geniale matematico Moessner nel 1951. Non è molto diverso da quanto abbiamo fatto precedentemente, ma è necessaria molta attenzione. In fondo, è solo un gioco da bambini (dovete, però, avere a disposizione un bel mucchio di sassolini e … tanta fantasia.

Partiamo di nuovo con la solita serie dei numeri interi. Il primo passo è quello eliminare un numero sì e uno no. In altre parole, eliminiamo il secondo numero, poi il quarto e via dicendo. Come abbiamo visto si ottengono i numeri quadrati (Fig. 1b).

Riprendiamo la serie completa ed eliminiamo, adesso, il terzo, il sesto e via dicendo (due li teniamo e uno lo eliminiamo). Seguendo il solito procedimento di sommare e riportare in seconda riga abbiamo adesso una strana serie che ci dice ben poco (Fig. 3).

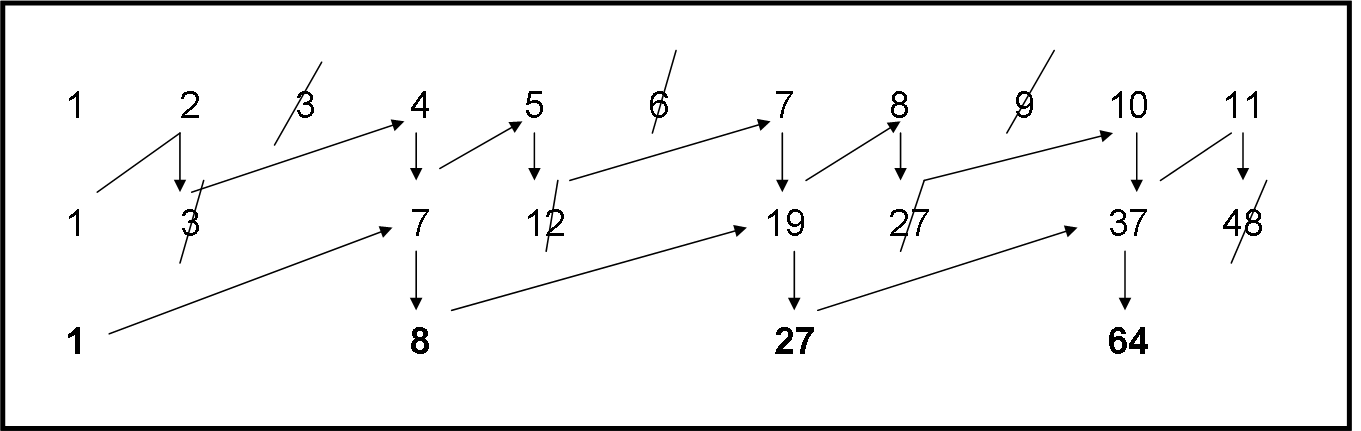
Non occupiamocene, anche se sicuramente ha una sua logica: non possiamo scoprire l’interno Universo, o -meglio- gli infiniti Universi “a due dimensioni”, in un colpo solo… Calma e sangue freddo. Teniamoci la nuova serie. Su di lei operiamo come fatto per trovare i quadrati, ossia, eliminiamo un numero sì e uno no… Fatto?

Bene,  abbiamo ottenuto una nuova serie di numeri: 1, 8, 27, 64, …

Non discutiamone ancora e proseguiamo con la Fig. 4.

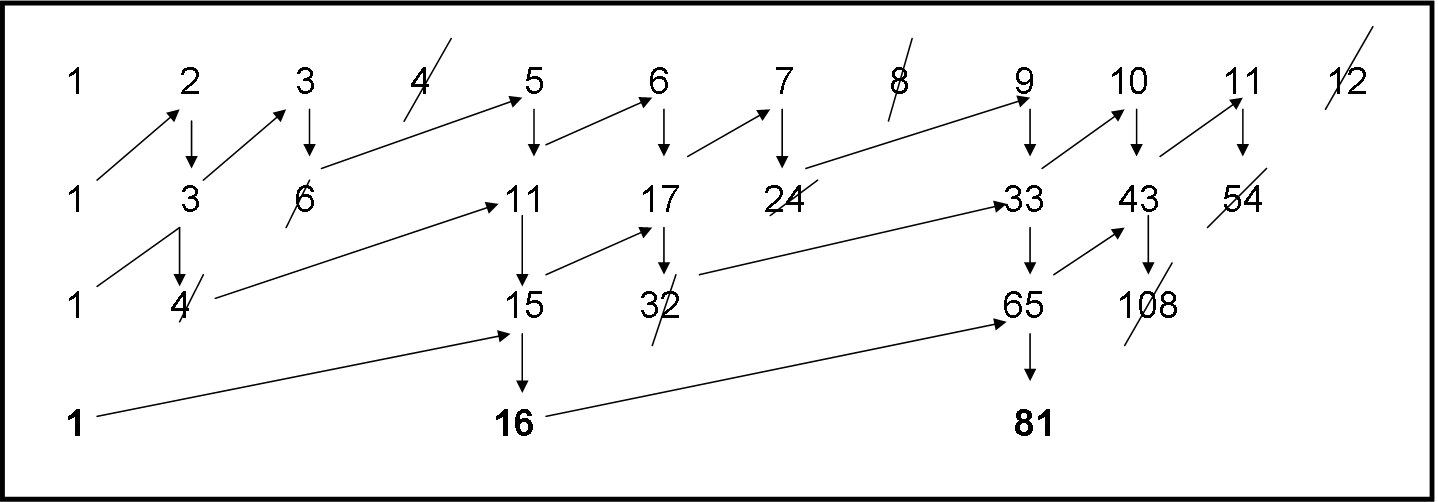
Partiamo sempre dalla solita serie completa, però, eliminiamo il quarto numero (tre salvati e uno cancellato). A questo punto facciamo la ben nota operazione e costruiamo la seconda linea, composta da: 1, 3, 6, 11, 12 , 19, 27, 48, … Un mondo del tutto astruso e conosciuto. Non ci curiamo di lui e proseguiamo: eliminiamo un numero ogni 2 e otteniamo la serie della terza riga: 1, 4, 15, 65, 108, …. Ancora un passo e da questa riga eliminiamo un numero sì e uno no. Si ottiene, infine, la quarta riga: 1, 16, 81, …

Non ne avreste più bisogno, dato che penso abbiate capito dove si arriva proseguendo nel “gioco”. Comunque, in Fig. 5 ricominciamo da capo e cancelliamo il quinto numero. Si costruisce una nuova riga, dove si elimina il quarto numero; un’altra riga e eliminiamo il terzo numero; un’altra riga e eliminiamo il secondo numero. Costruiamo, infine, l’ultima riga e si ottiene la serie: 1, 32, 243, ...

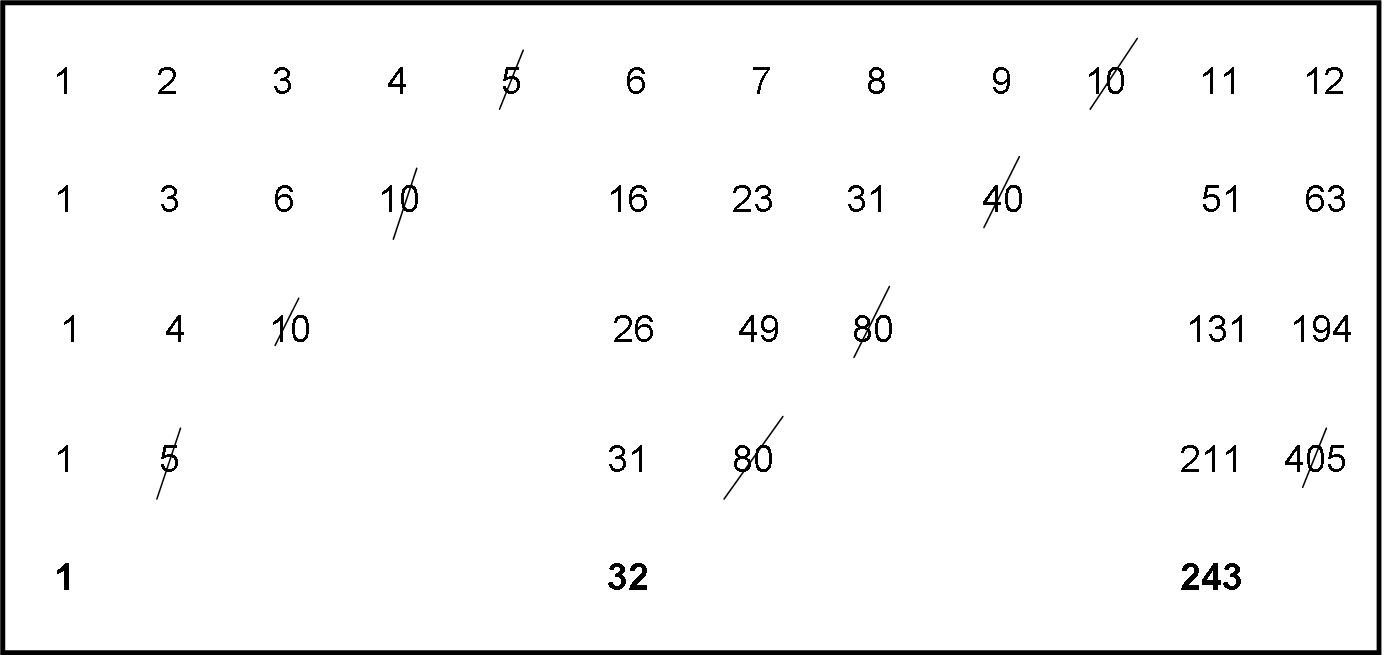
Ricapitoliamo:

Eliminando il secondo numero otteniamo: 1, 4, 9, 16, 25, …   =  1², 2², 3², 4², 5²

Eliminando il terzo numero otteniamo: 1, 8, 27, 64, …  =  1³, 2³, 3³, 4³

Eliminando il quarto numero otteniamo: 1, 16, 81, …   =  1⁴, 2⁴, 3⁴

Eliminando il quinto numero otteniamo: 1, 32, 243, …  =  1⁵, 2⁵, 3⁵

In realtà, possiamo anche aggiungere, all’inizio, la serie di tutti i numeri (senza eliminarne nessuno).

Ricordandoci che ogni numero può essere rappresentato da un mucchio di sassolini, non è difficile costruire la Fig. 6 che ci porta dritti dritti verso un altro tipo di Universi paralleli.

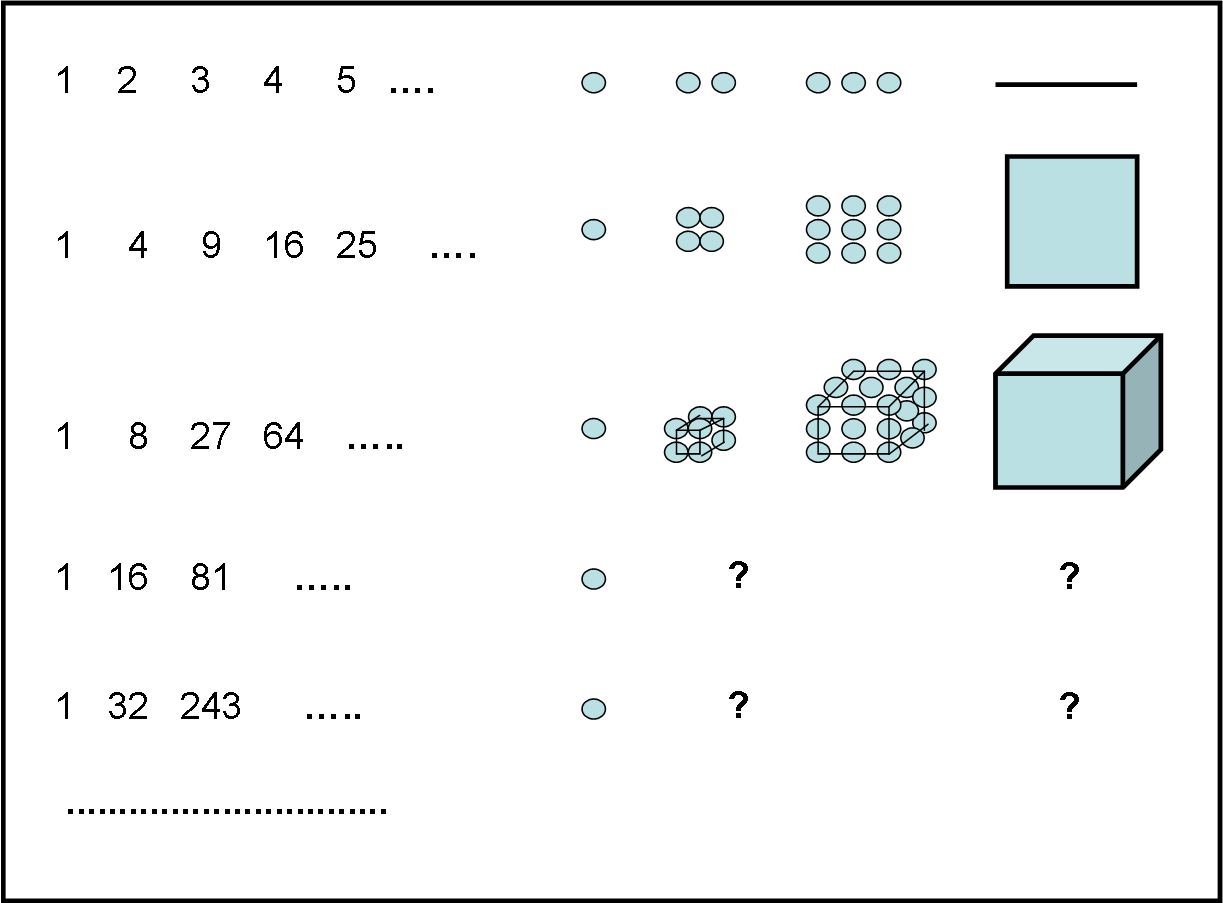
Il primo è quello LINEARE, a UNA DIMENSIONE

Infatti ogni numero può essere rappresentato con un sassolino, due sassolini, tre sassolini, posti uno a fianco dell’altro. In pratica disegniamo dei segmenti.

Il secondo è l’Universo QUADRATO, A DUE DIMENSIONI

Infatti, ogni numero può essere disegnato con un quadrato che ha 1, 2, 3, 4 sassolini come lati

Il terzo è l’Universo CUBICO, a TRE DIMENSIONI

Infatti ogni numero (chiamiamolo attore) può essere rappresentato come un cubo che ha 1, 2, 3, 4, … sassolini come spigoli

Il quarto è l’Universo a QUATTRO DIMENSIONI… ma come possiamo rappresentarlo attraverso i sassolini? Purtroppo noi non siamo in grado di farlo. Siamo ancora troppo primitivi. I numeri ci superano senza problemi…

E pensare che il gioco può andare avanti fino a qualsiasi dimensione n-esima, ma noi non sapremmo cosa fare dei nostri sassolini. Eppure questi numeri esistono sicuramente e riusciamo, con molta limitatezza, a scriverli con delle cifre. Ma la loro vera essenza e quella dei rispettivi Universi ci è vietata!

Non ci sarà passato inosservato il fatto che certi “numeri” (ma parliamone con molto rispetto) appartengono a Universi di dimensioni diverse. Ad esempio, il 16 appartiene a quello a due e a quattro dimensioni. Un punto di passaggio tra Universi diversi? I numeri ce lo stanno indicando, ma noi siamo ancora troppo limitati per seguire le loro indicazioni… Certi numeri hanno stati diversi nello stesso Universo a due dimensioni (possono essere poligoni diversi), ma altri rappresentano stati diversi in Universi a dimensioni diverse (possono essere quadrati – a due dimensioni-  ma anche “attori” a quattro dimensioni).

La cosa più importante è, comunque, che noi non siamo capaci di costruire numeri con dimensioni maggiori di tre. Siamo o non siamo ben piccola cosa rispetto a loro?

Pensate, poi, che nell’Universo a tre dimensioni potremmo benissimo costruire piramidi, esaedri e quello che volete… Infiniti Universi all’interno di ogni Universo a n dimensioni. E che dire poi se ripetessimo la nostra operazione delle righe sovrapposte a serie di numeri già selezionati (triangolari ad esempio?). E se sommassimo in qualche strano modo interi Universi n-dimensionali…?

La testa ci sta girando… altro che stringhe, brane, multiversi a 6 o 7 dimensioni, materie brillanti o oscure…

In ogni modo, per restare con i piedi per terra, attraverso la costruzione che ci ha permesso di costruire infiniti Universi numerici -teorema di Moessner-  siamo in grado di calcolare tutte le potenze dei numeri naturali facendo delle semplici somme…

Va bene, va bene… torniamo ai nostri numeri perfetti (bastano e avanzano)

 

QUI potete trovare tutti gli articoli sull'Universo dei Numeri