2° Quiz del Club dei maghi: Una gara un po' strana..
Ciao amici terricoli!
Mi chiamo Quazel, provengo da un piccolo pianeta con due Soli situato in quella zona di cielo che voi chiamate costellazione dell’Aquila, e sono appena arrivato sul vostro pianeta!
Dopo essermi sottoposto con pazienza a tutti i test preparati dai vostri scienziati e averli brillantemente superati (se non ci credete, leggete QUI), lasciate che mi diverta un po’ a proporvi un semplice quiz che va molto di moda sul mio pianeta.
Nel mio mondo i protagonisti di questo quiz sono un simpatico trilodonte isomorfo e un affabile garpentino xiloniano… qui sulla Terra, in mancanza di meglio, dovrò accontentarmi di una tartaruga e di una lumaca!
Ma, bando alle ciance, veniamo al sodo!
La tartaruga e la lumaca partono da uno stesso punto P (Partenza) ai bordi di uno stagno circolare, che coincide con il punto A (Arrivo). La lumaca ha una velocità tale che impiega 12 ore a fare il giro completo dello stagno, mentre la tartaruga ha una velocità 12 volte superiore.
La domanda è: ogni quanto tempo la tartaruga doppia la lumaca, prima che la lumaca torni in P=A?
Ci sono molti modi per arrivare alla soluzione, il mio preferito è il più breve, basato solo su una semplice divisione e un po’ di logica matematica! Ma tutti sono ammessi, l’importante è dare la risposta giusta.
Forza ragazzi, stupitemi!!! Il quiz rimarrà aperto per una settimana
Quazel (in collaborazione con Umberto, Arturo e Valentina)
QUI la soluzione del quiz
QUI trovate tutti i quiz proposti dal Club dei Maghi
23 commenti
Ogni 65 minuti?
top secret Gimar, però in ogni caso la risposta va giustificata; Quazel é molto fiscale...
Poiché in 12 ore sarà doppiato 11 volte, sarà doppiato ogni 65,45 minuti con 45 periodico cioè ogni 12/11 ore
12ore per 60 minuti=720minuti
720minuti diviso 12=60minuti
Bravo Gigi !
Ormai li fanno tutti digitali....anzi, le persone non li comprano più , guardano il telefonino....
Ma io ho una vecchia cipolla di mio nonno , e ho fatto la prova pratica ...
Si tratta di 1h , 5min , e 27 s circa ...
C'è anche una dimostrazione più analitica...ma io non dico più niente .
Ma come Quazel vai di fretta! Vuoi la matematica ? Te la dò , però poi non lamentarti che il Quazelquiz è stato risolto troppo presto.
La lumaca L ha una velocità 12 volte inferiore a quella della tartaruga T . Esse descrivono entrambe la stessa circonfernza, di lunghezza
, dove 
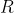è il raggio . Siccome la velocità periferica nel moto circolare uniforme è :
ed R è lo stesso per entrambe, la velocità angolare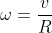
è proporzionale alla velocità periferica .
Quindi , L esegue il percorso da P ad A in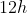
, e la sua velocità angolare è :
perciò T ha una velocità angolare 12 volte più grande :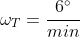
Qual è l'istante di tempo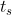
(espresso in minuti) del primo sorpasso di T rispetto a L ? il raggio vettore OT ( O è il centro ella circonferenza, OT è il raggio che unisce O alla posizione istantanea di T ) deve descrivere un angolo superiore a 
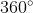, infatti nello stesso tempo L si è spostata pure lei , con la sua velocità angolare 
; quindi il primo sorpasso si avrà quando :
cioè :*t_s&space;=&space;360^{\circ})
cioè :
con (45) periodo .
Sono quindi :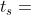
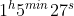circa .
Ma la soluzione di Gigi è la più rapida , e lascio a lui la spiegazione .
Scusate, all'inizio del post volevo dire : Quazel, ma come vai di fretta ! Ho fatto una involontaria permutazione, non volevo essere volgare !
Quazel, comincio a capire il motivo per cui sei arrivato qui sulla Terra : i tuoi com-planetari ti hanno dato un grosso calcione nel lato B , sicché hai acquistato una bella velocità , ben superiore alla velocità di fuga non dal pianeta, nè dal sistema planetario della tua stella, ma addirittura dalla galassia in cui essa si trova!
Il motivo, per me, è semplice : non hai mai voluto imparare per bene la fisica , e quindi....pussa via! Mi sa che ti rispedirò sul pianeta Q !
Dunque , che dici ? Se T ed L fossero due pianeti ? Sulla stessa orbita circolare di raggio R , attorno alla stessa stella (ovviamente) ? E magari, perchè non aggiungi anche, cosí tanto per complicare le cose , che T ha una massa 100 volte quella di L ???
La fisica ci dice che T non potrebbe avere una velocità 12 volte maggiore di quella di L , a meno che T non abbia dei potenti motori a reazione, e corregga in continuità la rotta per non andare fuori orbita . Sulla stessa orbita circolare , di raggio R , sia T che L devono avere la stessa velocità , determinata solo dalla massa M della stella:
dove G è la costante di gravitazione universale , M la massa della stella che crea il campo gravitazionale, R il raggio dell'orbita.
Pezzo di Quazel, se non lo sai questa si chiama "prima velocità cosmica" , e si ricava imponendo la condizione che la forza di attrazione gravitazionale funzioni da forza centripeta sul pianeta :
da cui la massa m del pianeta si semplifica, e si ricava v come sopra detto. Quindi T ed L devono procedere con la stessa velocità sulla stessa orbita , e tra di loro sono in quiete relativa.
E adesso ti faccio io una domanda : quale deve essere il rapporto tra i raggi delle orbite, se vogliamo che il rapporto tra la velocità periferica di T e quella di L sia 12 ?
Un po' di matematica , prego....se ne sei capace !
Per i lettori che vogliono partecipare costruttivamente al QUIZ chiarisco il suggerimento che coinvolge i pianeti:
è ovvio che fisicamente non sta in piedi, ma il calcolo del periodo sinodico si può applicare benissimo anche a moti circolari qualsiasi e non solo a pianeti che seguano le leggi di Keplero... La parola pianeti doveva solo far pensare alla problematica dei periodi reali e di quelli sinodici, che vale comunque. Nella realtà Lumaca e Tartaruga non si mettono a fare gare e sicuramente neanche Quazel esiste..
Io scherzo , Umberto , ovviamente ....Qui di fisico non c'è praticamente nulla , è solo un gioco matematico.
Non intendo imbarcarmi in discussioni di orbite planetarie e meccanica celeste . Ho risposto al quiz con la matematica che voleva l'alieno , nient'altro .
ovviamente l'ultimo commento scritto non era per te, e c'è anche scritto chiaramente in grassetto..era solo per permettere ai lettori di pensare ad una soluzione alternativa.
Poiché la lumaca fa un giro in 12 ore e la tartaruga fa 12 giri, ma nel primo giro non effettua doppiaggi, questo significa che in 12 ore fa solo 11 doppiaggi, quindi un doppiaggio ogni 12/11 ore
si Gigi avevamo visto la tua risposta. Per adesso posso solo dirti che quazel mi sembra contento.
ciao, penso che il riferimento alle lancette dell'orologio non sia casuale... Comunque ci ho pensato un po' e sono arrivato a quanto segue:
come per le lancette dell'orologio il numero di giri che la tartaruga deve compiere perche la lumaca ritorni al punto di inizio e' sempre uno in piu' rispetto al numero di incroci. Infatti al completamento del primo giro la lumaca si e' spostata di un poco, e quindi il primo incrocio avverra' il giro successivo.
In 12 giri necessari alla tartaruga perche' la lumaca completi un giro ci saranno solo 11 incroci. Per sapere ogni quanti giri avverra' un incrocio dovrebbe bastare dividere uno per l'altro: 12/11 fa 1,09 che significa che ci sara' un incrocio ogni 1,09 giri (se la tartaruga impiegasse un'ora allora ci sarebbe un incrocio ogni l,09 ore che messo in sessantesimi dovrebbe dare 1 ora, 5 minuti e 27 secondi.
si puo' credo generalizzare, perche' il numero di incroci e' sempre uno meno del numero di giri, che a loro volta dipendono dalla differenza di velocita'. Se la tartaruga andasse solo 3 volte piu veloce della lumaca, allora i giri sarebbero 3, gli incorci 2, e ci sarebbe un incroco ogni 2/3 giri, cioe 1,5 giri. Se fosse 4 volte la velocita' sarebbero 4/3=1,333 giri.
Ho postato la mia prima di leggere i commenti, e vedo che Gigi aveva gia' dato la soluzione a cui ho pensato anch'io. Bravo. Nell'ultimo esempio ho anche fatto un errore: con velocita tripla avremmo 3 giri diviso 2 incroci (non il contrario), fa 1,5 giri per ogni incrocio.
Volevo provare ad accettare l'invito di Quazel a trattare lumaca e tartaruga come se fossero due pianeti con orbite circolari.
Nel quiz la lumaca impiega 12 ore per compiere un giro completo, ossia questo è il suo periodo di rivoluzione intorno al comune centro.
Periodo rivoluzione della lumaca PL = 12 ore
La sua velocità angolare si ricava in un attimo:
Velocità angolare Lumaca: ωL = 2π/PL
PL= 2π/ωL = 12 ore
Nel quiz la velocità angolare della tartaruga è 12 volte superiore a quella della lumaca.
Dato che le orbite sono circolari entrambe le velocità angolari sono costanti.
La velocità angolare della tartaruga è anch'essa facilmente ricavabile:
ωT = 2π/PT
Ne segue che il Periodo di rivoluzione della Tartaruga è pari a:
PT= 2π/ωT
ma ωT = 12 ωL
PT= 2π/12 ωL
ma 2π/ωL = PL
Perciò il Periodo rivoluzione della tartaruga
PT = PL/12 = 12 ore/12 = 1 ora
Ciò che si deve ricavare è il Periodo sinodico tra i due pianeti (nel nostro caso tra i due contendenti), ossia l'intervallo di tempo che separa un incontro dall'altro, un doppiaggio dall'altro.
Quando la Tartaruga ha compiuto 1 giro completo, la Lumaca si è mossa dalla partenza ed ha compiuto una frazione di giro (1/12 di giro).
Quindi, per raggiungere e doppiare la Lumaca serve ancora un certo intervallo di tempo, quello necessario alla Tartaruga per compiere un tratto supplementare di giro oltre il suo periodo orbitale (PT)...
La lumaca per girare intorno al centro esattamente come la Tartaruga dovrebbe correre più velocemente, ossia la sua velocità angolare dovrebbe aumentare fino a raggiungere ωT= 2π/PT, ossia:
ωT = ωL + Δω
Δω = ωT - ωL
Questa differenza di velocità angolari si traduce in un angolo diverso percorso nella stessa unità di tempo.
Considerato che:
ωT = 2π/PT e ωL = 2π/PL
Δω = 2π/PT - 2π/PL
Perciò affinché la tartaruga possa doppiare la lumaca, ossia affinché la Tartaruga e la Lumaca possano trovarsi allineati deve passare un certo Periodo di tempo detto sinodico Psin , che si può ricavare proprio partendo dalla relazione che lega le velocità angolari, dato che Δω = 2π/Psin:
2π/Psin = 2π/PT - 2π/PL
2π/Psin = 2π (1/PT - 1/PL)
2π/2π Psin = (PL - PT)/(PT PL)
1/Psin = (PL - PT)/(PT PL)
Psin = (PT PL)/(PL - PT)
Per trovare il periodo che intercorre tra un doppiaggio e l'altro basta sostituire i valori dei due Periodi orbitali:
PT = 1 ora e PL = 12 ore
Psin = (1) (12)/(12 – 1) = 12/11 = 1,090909 ore
Per trasformarlo in minuti basta moltiplicarlo per 60:
Psin = (1,090909) 60 = 65,454545 minuti
Per trasformarlo in secondi basta moltiplicare la relazione iniziale per 3600:
Psin = (1,090909) (3600) = 3927,272727 secondi
Il metodo sembra più lungo, solo perché ho ricavato le formule, altrimenti bastava applicare la formuletta:
Psin = (PT PL)/(PL – PT) per risolvere il quiz velocemente.
mi hanno inviato un filmato inedito che riprende un trilodonte isomorfo e un garpentino xiloniano che stanno gareggiando… 
Un ultima precisazione, avendo usato le velocità angolari, la formula è valida anche se la Lumaca e la Tartaruga non sono pianeti... si potrebbe pensare che ruotano intorno al centro legati ad esso da una barra rigida (un po' come le lancette di un orologio)....
Nel caso di pianeti, ovviamente l'orbita di quello più veloce sarebbe più stretta (vicino al centro) rispetto a quella del pianeta più lento.... e il Periodo sinodico trovato indicherebbe l'intervallo tra un allineamento e l'altro tra i due pianeti rispetto al centro di rotazione (un sorpasso a distanza).
Ah dimenticavo... i miei amici papalliani
...se il filmato non dovesse funzionare questo è link : http://postimg.org/image/5wl12yo1v/
Paolo
Grande Paolino, sei un mito!!
Paolo dice: "Nel caso di pianeti, ovviamente l'orbita di quello più veloce sarebbe più stretta (vicino al centro) rispetto a quella del pianeta più lento.... e il Periodo sinodico trovato indicherebbe l'intervallo tra un allineamento e l'altro tra i due pianeti rispetto al centro di rotazione (un sorpasso a distanza)".
Bravo, ma un po' conservatore... dovrebbe riflettere meglio sulla spiegazione di Quavel che ammette P diversi anche sulla stessa orbita... Keplero e Newton sono ormai obsoleti... (e anche la RG)...
Eppure mi avevano assicurato che la gara si è svolta sotto vuoto quantico, stando attenti a non stropicciare troppo lo spaziotempo, al fine di ridurre le probabilità che si imbizzarriscano le costanti.
Comunque anche se i pianeti si dovessero muovere a velocità diverse sulla stessa orbita, diventerebbero obsoleti Keplero, Newton e la RG, ma l'uso del Periodo Sinodico sopravvive...
Paolo
va bene, va bene... ti sei salvato in corner...
(ma che non ti senta il vuoto che hai considerato vuoto quando lui sa che non è vuoto...insomma qualcosa del genere... 
)