Siamo giunti alla formula risolutiva, a quella che lega curvatura con massa/energia. Curvato il tempo, dovremo affrontare una piccola lotta tra RR e RG per descrivere il moto di tutto ciò che finisce nei pressi di una massa con una densità importante. Anche la luce deve inchinarsi alla legge forse più rivoluzionaria della Scienza.

Cerchiamo di quantificare in modo molto semplice la “curvatura” del tempo, collegata ovviamente a quella dello spazio (la Relatività Ristretta non perdona e ci torneremo al momento giusto).

Curviamo il tempo

Torniamo sulla nostra astronave (QUI) con i due orologi in A e B. Consideriamo come buona la formula che regala l’effetto doppler relativistico (prima o poi la ricaveremo, ricordando però che parliamo di un vero effetto doppler e non di uno spostamento verso il rosso, ossia è il classico effetto doppler ma con una velocità di spostamento della sorgente che sia comparabile con quella della luce). Essa dice:

f  = fo (1 + v/c)/(1 - v²/c²)          …. (1)

dove fo e f sono le frequenze misurate alla partenza dall’emettitore e all’arrivo al ricevitore. In realtà, nel nostro caso, le velocità dell’emettitore e del ricevitore sono uguali (sembrerebbe che non ci sia velocità della sorgente rispetto al ricevitore). Ciò non è, però, vero… dato che l’astronave accelera e quindi durante il viaggio della luce da A a B (H) vi è un aumento di velocità data da gt dove g è l’accelerazione e t è il tempo impiegato ad andare da A a B. Il tempo t può essere approssimato da H/c. Ne segue che quando il segnale arriva in B, la velocità dell’astronave è aumentata del valore:

gt = gH/c

Questa è sempre la velocità relativa tra ricevitore ed emettitore e può quindi essere considerata come la velocità di spostamento da inserire nella (1). Considerando molto piccole la distanza H e l’accelerazione g, v risulta decisamente minore di c e possiamo trascurare nella (1) il termine v²/c².

La (1) diventa:

f = fo (1 + gH/c²)      …. (2)

In parole: la frequenza dell’orologio del ricevitore è uguale alla frequenza dell’emettitore moltiplicata per la quantità:

(1 + gH/c²)

Per il principio di equivalenza, tutto ciò che capita in un astronave che ha un accelerazione g, deve capitare anche in un campo gravitazionale che ha un’accelerazione di caduta libera uguale a g.

La relazione (2) si può anche dimostrare in altro modo. Il fotone parte dall’orologio superiore con una certa energia data da:

 E_A = fo h

 Dove h è la costante di Planck e fo la frequenza del segnale alla partenza.

 La sua massa relativistica (l’abbiamo spiegata nella parte finale di questo articolo) è:

 m_F = E_A/c²

 m_F = fo h/c²

 "cadendo” verso la terra (l’accelerazione dell’astronave è equivalente a una caduta verso terra a causa della gravità) si recupera l’energia potenziale tra A e B. Essa vale:

 E_AB = m_F g H     (H è la distanza tra A e B)

 All’energia del fotone “in caduta” si deve aggiungere questa energia e si ottiene:

 E_TOT = E_A + E_AB  = fo h +  m_F g H  =  fo h + fo hgH/c² = fo h(1 + gH/c²)

 Tuttavia, E_TOT non è altro che l’energia che arriva in B che è data da :

 Etot = E_B = f  h

 Dove f è la frequenza, ovviamente cambiata. Si ha subito il rapporto tra le due frequenze, quella di ricezione e quella di emissione:

 f  h = fo h(1 + gH/c²)

 f = fo (1 + gH/c²)         …. (2)

Tutto ciò in perfetto accordo con quanto rilevato dagli orologi. Quello in B vede la frequenza dei segnali inviati da A più alta. Ossia, quello in B è più lento. Ma, adesso, abbiamo anche quantificato il fattore di rallentamento attraverso le frequenze.

La strana “piastra” curva lo spaziotempo

Abbiamo già capito che tutto ciò che comporta una differenza di tempo in zone diverse è analogo a quanto avevamo trovato per una piastra che scalda al crescere della distanza. Ma il risultato è ben più che un’analogia: lo spaziotempo è proprio curvo. Vediamolo meglio con una semplice serie di figure nello spaziotempo. Figura che abbiamo usato spesso e volentieri, considerandole figure essenzialmente geometriche. In ascissa c’è lo spazio e in ordinata il tempo.

Cerchiamo di costruire un rettangolo in questo sistema di coordinate. Il nostro spaziotempo (un solo sistema di riferimento) è immerso in un campo gravitazionale. Partiamo da un punto B e immaginiamo che sia fermo. Esso segue la sua linea di Universo parallela all’asse del tempo. Questo “lato” del rettangolo valga esattamente 100 sec (del suo tempo proprio, ovviamente). Il primo lato è quindi BD (Fig. 1a)

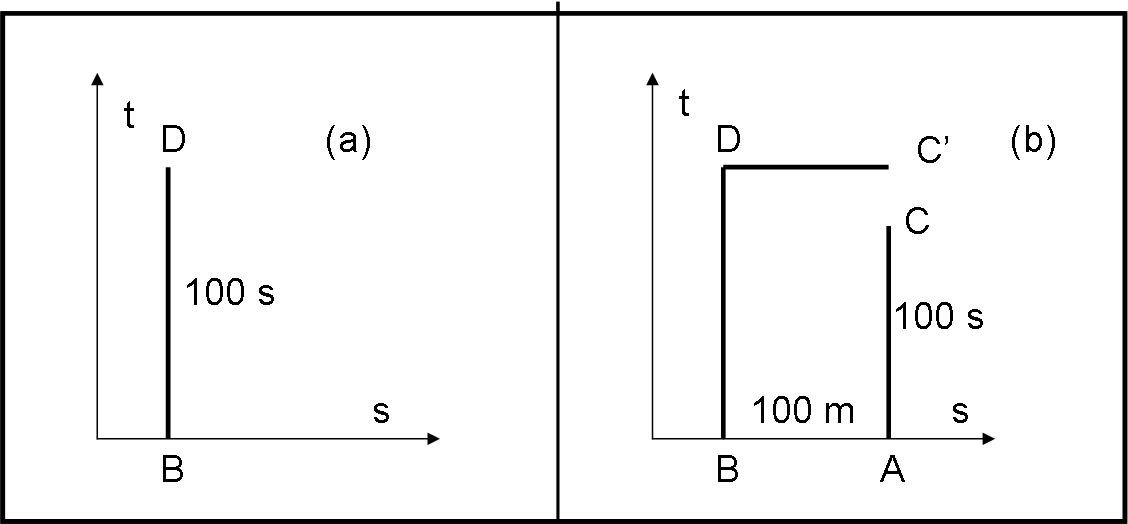
Prendiamo adesso un altro punto A che stia a 100 m di distanza da B. Immaginiamo che anch’esso sia in quiete. Misuriamo nuovamente 100 sec con il suo orologio e ci fermiamo nel punto C corrispondente. Abbiamo appena dimostrato, però, che due orologi posti a una distanza (altezza) tra di loro (A è più ALTO di B nel campo gravitazionale) girano in modo diverso. In particolare A va più veloce di B e raggiunge prima i 100 sec. In poche parole il lato AC è minore di BD. Dobbiamo concludere che i punti C e D NON sono simultanei. Se tracciamo la linea di simultaneità di D (parallela all’asse dello spazio), fino all’oggetto A, essa termina in C’ (Fig. 1b).

Attenzione, siamo in RR, ma non vi è nessun movimento di un sistema rispetto a un altro. Qui siamo in un solo sistema di riferimento: la simultaneità deve mantenersi. Tuttavia, il nostro rettangolo non si chiude, dato che C’ NON coincide con C. Non ci resta che concludere che la geometria del piano considerato non è euclidea, ossia che lo spaziotempo è CURVO.

Vi prego di non considerare banale questa trattazione… Ci siamo messi nello spaziotempo di Minkowski, abbiamo tracciato le linee di Universo di due oggetti FERMI e abbiamo infine considerato la linea di simultaneità. Se il rettangolo spaziotemporale non si chiude vuol dire che lo spaziotempo immerso in un campo gravitazionale è CURVO. Così come succedeva a chi cercava di chiudere un rettangolo su una superficie sferica… ricordate? (QUI).

Siamo ormai vicini alla conclusione del nostro viaggio (giocoforza semplificato) verso la legge della relatività generale.

Abbiamo, perfino tralasciato di vedere come si comporta la luce in un campo gravitazionale… Bene, lo facciamo subito, utilizzando come al solito la nostra astronave e, poi, il principio di equivalenza…

Anche la luce deve curvare

Che la luce pieghi e tenda a cadere nello spaziotempo curvato, può essere dimostrato in modo estremamente semplice. Torniamo nel nostro razzo che si muove con una certa accelerazione. Noi siamo all’interno del razzo e questo è il nostro sistema di riferimento che equivale (ormai lo sappiamo bene) a un campo gravitazionale.

Qualcuno, esterno all’astronave, spara un raggio di luce che, ovviamente, procede in linea retta, dato che non vi è campo gravitazionale! (Fig. 2).

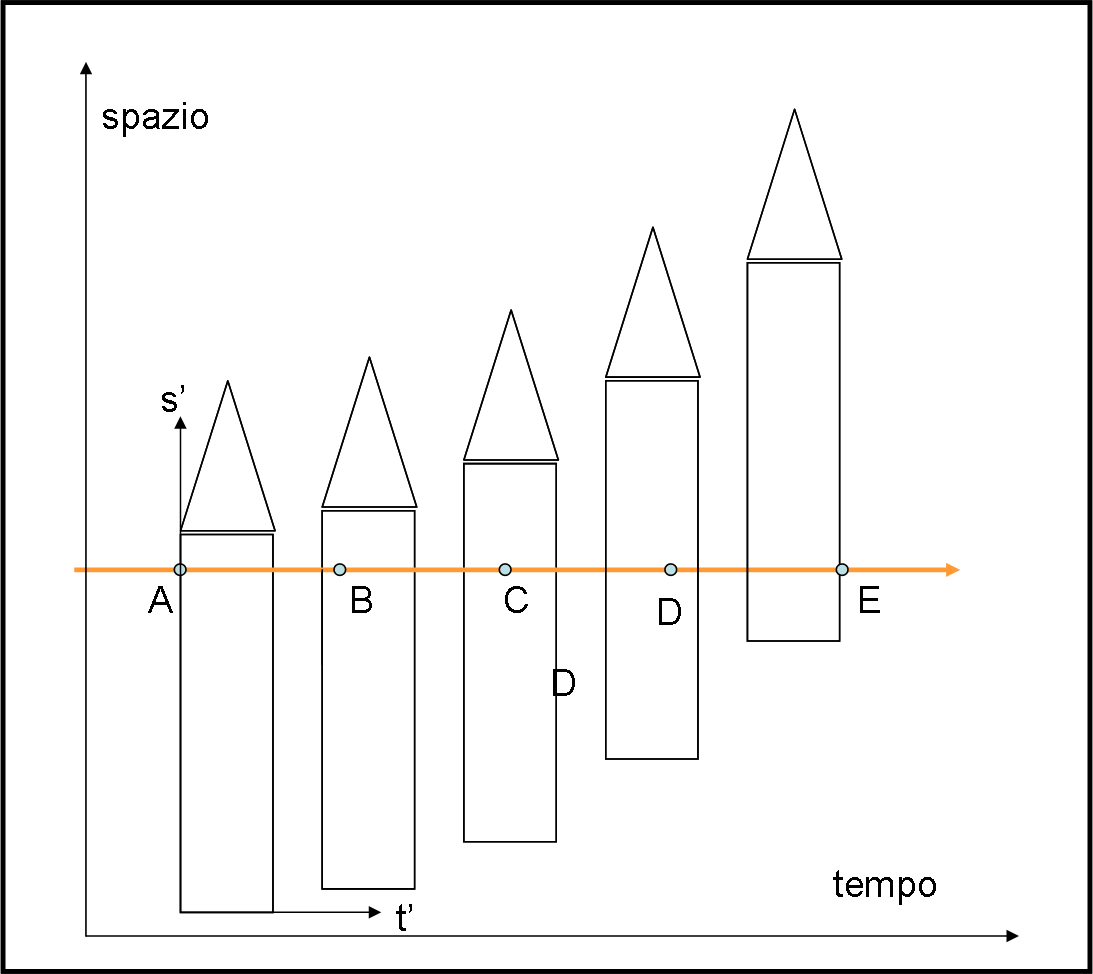
All’istante in cui entra all’interno dell’astronave (immaginata trasparente alla luce) la luce tocca la parte in A. Poi prosegue e giunge in B. Il suo moto sarebbe rettilineo, ma il pavimento dell’astronave si è alzato seguendo la variazione di velocità imposta dall’accelerazione. La stessa cosa succede in C, fino a che la luce esce dall’astronave in E, a un’altezza molto vicina al pavimento.

Per chi è all’interno dell’astronave (Fig. 3), la luce ha compiuto un percorso parabolico (è facile da calcolare), proprio come quello di un qualsiasi oggetto dotato di una certa velocità, immerso in un campo gravitazionale.

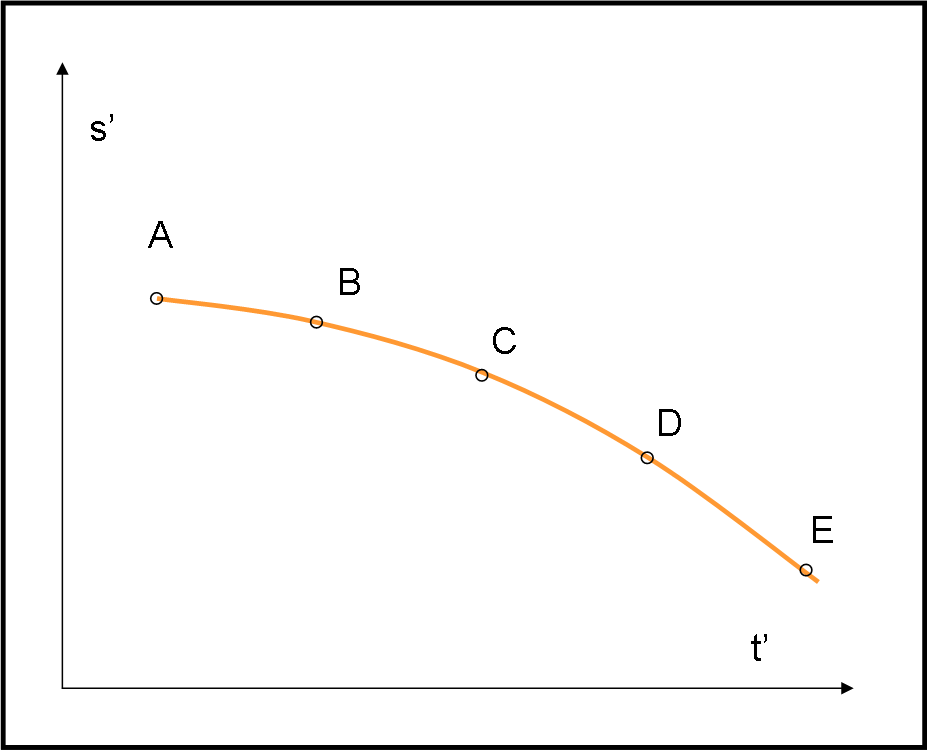
Ma, come ormai sappiamo bene, un’astronave accelerata equivale perfettamente a un campo gravitazionale e quindi possiamo tranquillamente concludere che la traiettoria della luce viene curvata dalla gravità, ossia segue perfettamente i binari dello spaziotempo secondo una traiettoria parabolica.

Uno scontro molto … relativo

Abbiamo fatto esempi molto particolari che ci hanno fatto capire come sia lo spazio che il tempo siano curvati dalla gravità e come perfino la luce sia obbligata a seguire certi binari ben predisposti dalla presenza di una massa. Non possiamo dimenticare, però, che vale comunque la Relatività Ristretta. Essa regala il legame vero che fa dello spazio e del tempo uno spaziotempo. Tutto ciò che agisce sul tempo deve agire anche sullo spazio e viceversa. In poche parole, le due relatività devono convivere. Spesso questa parte fondamentale viene un po’ dimenticata o raggirata. Esse non possono certo scontrarsi o arrivare a conclusioni diverse… Eppure, andando un po’ a fondo, sembrerebbe proprio.

Utilizziamo, tanto per cambiare, una specie di quiz che mette bene in  luce questa ipotetica contrapposizione.

Siamo sulla Terra. Io sono A e l’amico è B. I nostri orologi sono ovviamente sincronizzati. La mia intenzione è di fare “muovere” il mio orologio in modo che dopo cento secondi segni il tempo più lungo possibile. Beh… la cosa è, teoricamente, piuttosto semplice: lo faccio salire fino a una certa altezza, lascio che il mio orologio vada più veloce come abbiamo imparato QUI e all'inizio di questo articolo, e poi lo faccio scendere in B. Sicuramente dovrebbe segnare qualche secondo in più… E più in alto lo faccio andare e più secondi guadagna (Fig. 4, a sinistra).

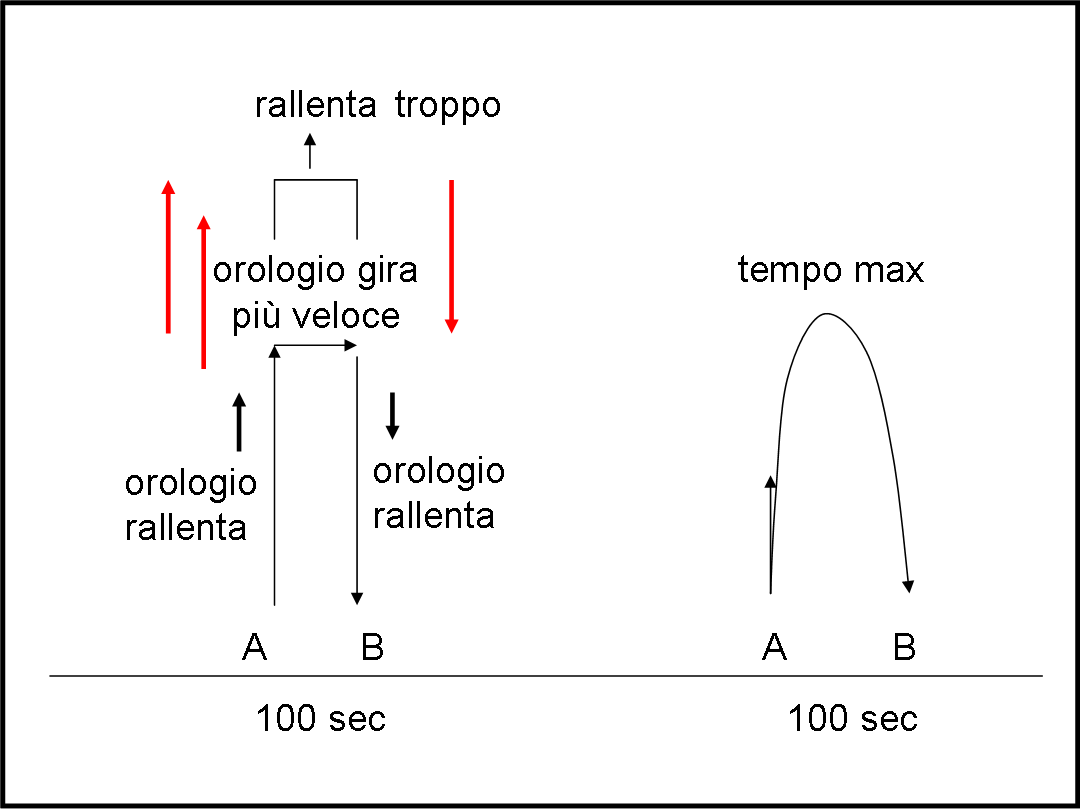
Sì, sì, teoricamente tutto bene. Attenzione però… per raggiungere una certa altezza  devo farlo muovere in qualche modo. Muoverlo, vuol dire impartirgli una certa velocità e per farlo arrivare il più in alto possibile (in modo da guadagnare più secondi) devo utilizzare una velocità molto alta. Ricordiamo, infatti, che il tutto deve compiersi esattamente in 100 secondi dell’orologio B.

E qui nasce un bel problema… Più è alta la velocità e più l’orologio rallenta a causa del maledetto fattore di Lorentz! Per diminuire al massimo il tempo del viaggio e sfruttare l’altezza raggiunta sono obbligato ad aumentare la velocità e, conseguentemente, a far rallentare al massimo l’orologio durante il viaggio. La faccenda è decisamente critica: siamo veramente di fronte a una lotta tra RR e RG!

Ricapitoliamo la situazione. Se non muovo per niente il mio orologio esso segnerà 100 secondi esattamente come quello di B. Ma io devo muoverlo (ossia voglio fargli descrivere un moto nel nostro spaziotempo). Se lo mando troppo lentamente in alto riesco a guadagnare qualcosa ma se lo mando troppo velocemente capita il contrario e l’orologio segna meno secondi. Qual è la soluzione più “naturale”?

Nient’altro che lanciarlo verso l’alto in modo che torni nelle nostre mani esattamente dopo 100 secondi. La rapida salita, il rallentamento, la fermata, e la ricaduta a velocità crescente è proprio ciò che ci vuole perché l’orologio misuri il tempo massimo.

Sospendiamo questo interessante giochino e rendiamolo più pratico. Prendiamo due punti A e B sulla Terra e cerchiamo il moto “rettilineo” tra A e B, ossia quello che permetta a un orologio di andare da A a B segnando il massimo tempo possibile. Ricordiamo, infatti, quello che abbiamo detto QUI : il moto rettilineo, ossia l’analogo di moto percorso a velocità uniforme, è il moto che obbliga un orologio a spostarsi da un punto in un dato istante (evento 1) a un altro punto  in un istante diverso (evento 2), in modo che esso segni il tempo più lungo possibile.

Attenzione, però, questo risultato era stato trovato utilizzando solo la relatività ristretta… bisogna cambiare qualcosetta, adesso, che siamo in un campo gravitazionale.

Combiniamo le relatività

L’idea è quindi quella di aggiustare un po’ il tiro e di non limitarsi alla linea a velocità uniforme. La cosa migliore da fare sarebbe di alzarsi un poco, ma non troppo, in modo da sfruttare al massimo la velocità maggiore degli orologi ad altezze superiori senza fare arrabbiare troppo la RR. Facendo i calcoli si trova nuovamente che la traiettoria ideale è quella parabolica, come, in fondo, abbiamo trovato precedentemente.

La legge del moto in un campo gravitazionale può, perciò, essere così enunciata, in modo generale e tenendo conto di quanto detto precedentemente: “Un oggetto si muove da un punto a un altro in modo che il suo orologio segni il tempo più lungo rispetto a qualsiasi altra traiettoria”. Ovviamente, al di fuori di un campo gravitazionale, la RR torna a giocare da sola, con tutte le sue regole.

N.B.: Utilizzando adeguatamente il diagramma di Minkowski si potrebbe descrivere come un'accelerazione (variazione continua della velocità) si possa inserire  nella relatività ristretta. In poche parole, è come se facessimo variare continuamente il sistema di riferimento in moto. In realtà, la RG potrebbe essere descritta approssimandola punto per punto con la RR. Al momento, però, preferiamo non entrare in dettagli e in trattazioni abbastanza complesse anche visivamente. Digeriamo prima una visione generale della RG. Poi, con calma, potremo anche andarla a sistemare all’interno del nostro diagramma di Minkowski.

 

Finora, abbiamo usato tante parole che ci hanno dato un’idea qualitativa che a molti potrebbe bastare. Tuttavia, non è molto difficile descrivere il moto nello spaziotempo con qualche formuletta. Newton ne sarebbe sicuramente contento.

La variazione di frequenza dovuta alla gravita è data dalla (2), in particolare al fattore:

fo gH/c²         …. (3)

Dobbiamo, però tener conto che vi è un fattore di segno opposto dovuto alla velocità (fattore di

Lorentz)

f = fo (1 – v²/c²)^1/2     …. (4)

La combinazione della (3) e della (4) porta al risultato voluto.

Noi eseguiamo il calcolo per una velocità v << c.

Ricordando gli sviluppi in serie (vedi lezioni di matematica da n° 43 a n° 50) si ha che:

(1 + x)^1/2 = 1 + ½ x + …

Ponendo

x = - v²/c²

si ha:

(1 – v²/c²)^1/2 = 1 - ½  v²/c²

La (4) diventa:

f = fo (1 - v²/2c²)

La variazione da combinare con la (3) è quindi:

- fo v²/2c²          …. (5)

La variazione totale di frequenza è quindi data dalla somma di (3) e di (5):

Δf = fo (gH/c² - v²/2c²)

Ciò vuol dire che se dt è il tempo (numeri di giri in un certo periodo di tempo) misurato da un orologio fermo, quello dell’orologio in modo è dato da:

dt (1 + (gH/c² - v²/2c²))

Ovviamente, la quantità “in eccesso” va integrata per tutto il periodo del moto. Il suddetto integrale deve essere un massimo:

1/c²∫ (gH - v²) dt = massimo

Prima di procedere ricordiamo che gH non è altro che il potenziale gravitazionale. Adesso, facciamo un giochino divertente. Moltiplichiamo l’integrale per la quantità -mc² sicuramente negativa. Il che vuol dire che l’integrale da massimo diventa un minimo, ossia l’oggetto si muove in modo che la nuova quantità sia un minimo. Proviamo a riscriverla …

∫ (- gHm + mv²/2) dt   = minimo.

Ma, attenzione: gHm è l’energia potenziale, mentre 1/2 mv² è quella cinetica, il che porta alle conclusioni descritte dalla legge di Newton (credetemi sulla parola!). La legge di Newton viene confermata dalla RG ipotizzando velocità di spostamento molto piccole. Einstein era proprio un mago!!

Riuscire a ritrovare la legge di Newton, stravolgendo completamente l’essenza del problema è un risultato che non poteva che sconcertare prima e strabiliare dopo.

Per sintetizzare la nuova visione einsteniana possiamo dire che Einstein cambia la gravità newtoniana in termini di geometria dello spaziotempo. La curvatura è ciò che comanda i movimenti degli oggetti e la massa è ciò che causa la curvatura. Più facile di così…

Le particelle seguono una ben definita legge muovendosi nello spaziotempo, ossia seguono le traiettorie (linee ferroviarie)  in cui gli orologi segnano il massimo tempo. Massimo tempo prende il posto di minima distanza nella visione newtoniana. In altre parole, il tempo proprio di una traiettoria deve sempre essere quello massimo.

La materia dice allo spaziotempo come incurvarsi, e lo spazio curvo dice alla materia come muoversi (J. Wheeler)

Conclusioni

Le leggi che governano la relatività generale sono, in pratica, due:

(1) Il cambiamento della geometria dello spaziotempo a causa della presenza di una massa. Esso  viene espresso come “eccesso” di raggio di curvatura, in funzione della massa, all’interno di una certa sfera (non confondiamo sfera con curvatura dello spazio; la sfera indica solo il volume in cui deve essere contenuta la massa), come ricavato QUI

(2) Il moto di un corpo soggetto solo alla gravitazione, ossia alla curvatura imposta dalla massa.

Queste due leggi sono molto simili a quelle su cui si basa la meccanica classica. La prima è la legge di Newton sull’inverso della distanza; la seconda è la descrizione del moto conseguente. La relatività generale potrebbe essere scritta semplicemente come:

R = GE

Dove R è una costruzione matematica composta da 16 numeri in una matrice o tensore che descrive la distorsione dello spaziotempo. Essa sarebbe in pratica ciò che Newton indica con F. G è la costante di gravitazione (quella resiste sempre). E è un altro numero molto complicato, descritto anch’esso da un tensore, che rappresenta l’energia dell’oggetto. In parole molto semplici il prodotto delle masse di Newton, ma con qualcosa in più…

Potremmo scriverla in modo molto più esteso, ma possiamo limitarci a questo:

R_μυ - ½ Rg_μυ = 8 πG T_μυ/c⁴

Dove R_μυ è il tensore di Ricci, R la curvatura scalare, g_μυ il tensore metrico, T_μυ il tensore energia-impulso. Non illudiamoci, però, essa sembra una sola equazione, ma in realtà dà luogo a molte equazioni dipendenti dalle componenti dei tensori. Tanto per dare una vaga idea di ciò che è contenuto in questo capolavoro, possiamo dire che bisogna tenere conto di tre dimensioni spaziali e di una temporale, che vengono evidenziate dalle lettere μ e υ che compaiono nei tensori. Il tutto può combinarsi in vari modi. Tant’è che le soluzioni dell’equazione, per le varie situazioni, non sono certo cose che possono farsi velocemente con carta e matita.

Non per niente, esse sono arrivate durante gli anni successivi e ancora ce ne sono probabilmente di segrete… E’ inutile proseguire se no si rischia di creare ancora più confusione. La formula precedente è quella a cui giunse Einstein dopo aver eliminato dal primo membro una costante Λ, con segno negativo, detta costante cosmologica. Einstein l’aveva introdotta per mantenere un Universo statico (l’errore più grande della sua vita, ebbe a dire). Quando Hubble scoprì che l’Universo era in espansione, quella costante venne tolta. Tuttavia, cambiandone il segno essa riuscirebbe a spiegare un’eventuale accelerazione dell’Universo e, di conseguenza, l’energia oscura… Tuttavia, quella costante potrebbe in qualche modo essere legata al vuoto-non vuoto e poter tornare utilissima. Chissà… Einstein era un genio anche quando sbagliava…

Appendice: La curvatura è veramente così difficile da descrivere?

Voglio lasciare da parte questa breve chiacchierata sulla curvatura, non perché sia difficile (anzi…), ma perché serve solo a riflettere sulla problematica mostruosamente complessa. Nella meccanica newtoniana siamo abituati a relazioni tra spazio e tempo (attenzione spazio e tempo e non spaziotempo), così come siamo abituati a descrizioni puramente geometriche nello spazio. Il vero problema di Einstein è che niente si può fare in una qualsiasi della quattro dimensioni senza che le altre ne siano influenzate. Ne segue, in parole molto povere, che, qualsiasi tipo di curvatura affrontiamo, siamo obbligati a considerarla sempre nello spaziotempo.Insomma, un problema di matematica VERAMENTE superiore…

Noi vogliamo solo illustrare qualche curvatura di ordinaria amministrazione, che affrontiamo normalmente, e che dà un contributo sostanziale nella parte di formula che è legata alla geometria spaziotemporale (quella di sinistra, ossia quella che descrive come ci si può muovere).

Consideriamo la Terra e scaviamo il famoso tunnel che passi da parte a parte. L’avevamo trattato ampiamente QUI. .

Il moto delle sfere lasciate libere in quel foro è influenzato solo dalla gravità (anche se definita in modo abbastanza peculiare). Tuttavia, pur rimanendo nell’ottica newtoniana è facile assistere a un andamento curvilineo di spazio verso tempo. Lo illustra perfettamente la Fig. 5, dove quattro palline sono lasciate libere (due vicino al boro esterno e due all’interno del tunnel). Come sappiamo esse oscillano impiegando lo stesso tempo a tornare al punto di partenza e quindi è facile vedere l’andamento dello spostamento rispetto al tempo. Nella prima parte le curve tendono a unirsi (curvatura positiva), nella seconda parte si allontanano (curvatura negativa). Situazioni analoghe capitano al di fuori della Terra.

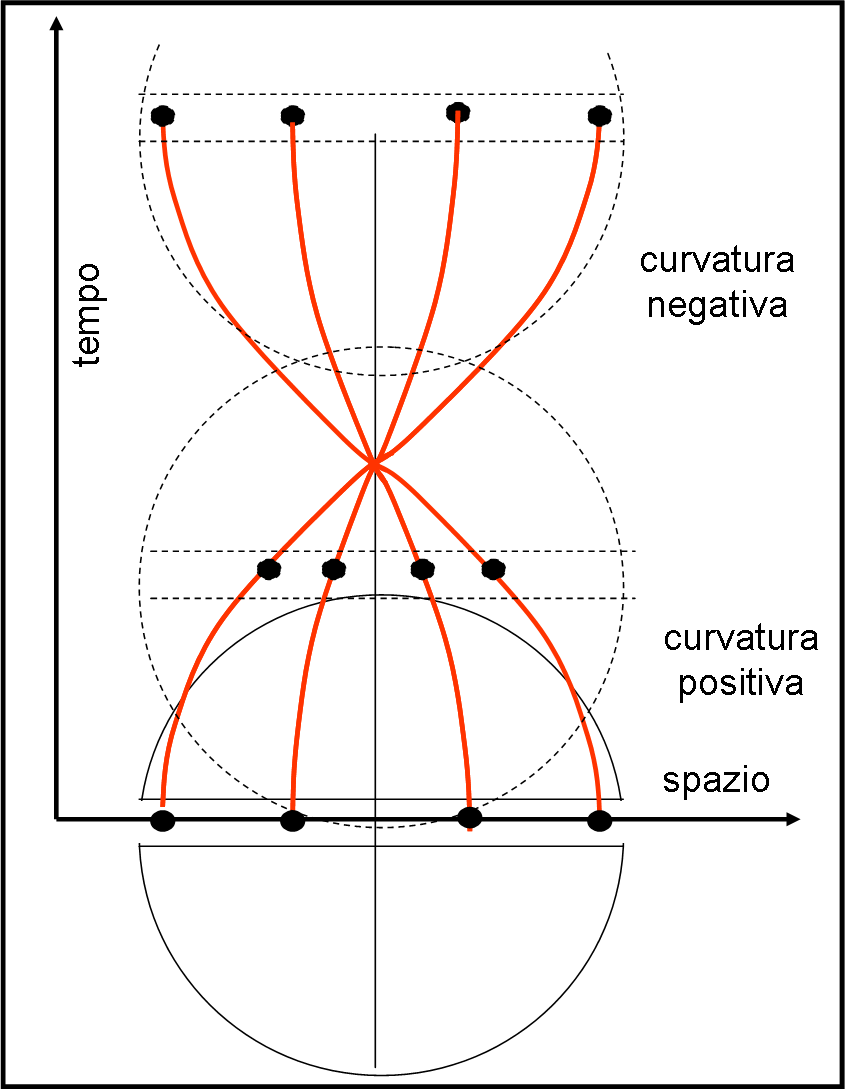
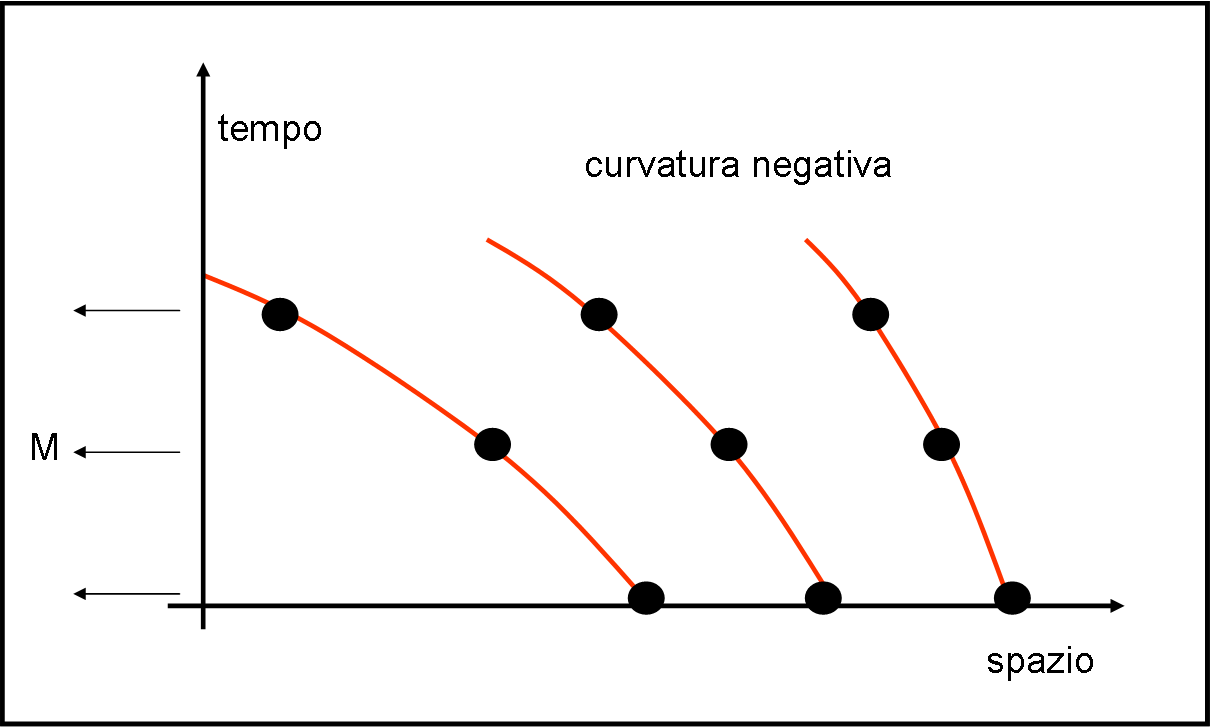
Consideriamo tre particelle che siano in preda alla gravità e che siano posizionate lungo la stessa direzione rispetto al centro di massa. Esse sono in caduta libera. Tuttavia, quella più lontana subisce una gravità minore di quella più vicina alla Terra, ossia la sua velocità è inferiore rispetto a quella più avanzata. Ne segue che il diagramma spazio in funzione del tempo descrive delle curve, per ogni pallina, che si discostano sempre più. Siamo di fronte a una curvatura negativa (Fig. 6).

Consideriamo, adesso, in Fig. 7, tre particelle che stiano tutte alla stessa distanza dalla Terra (qualsiasi piano andrebbe bene).

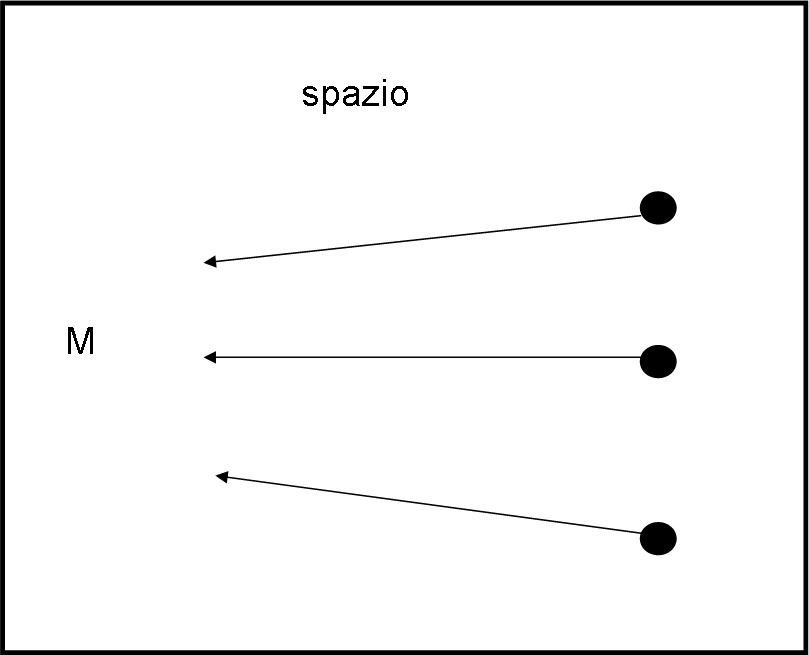
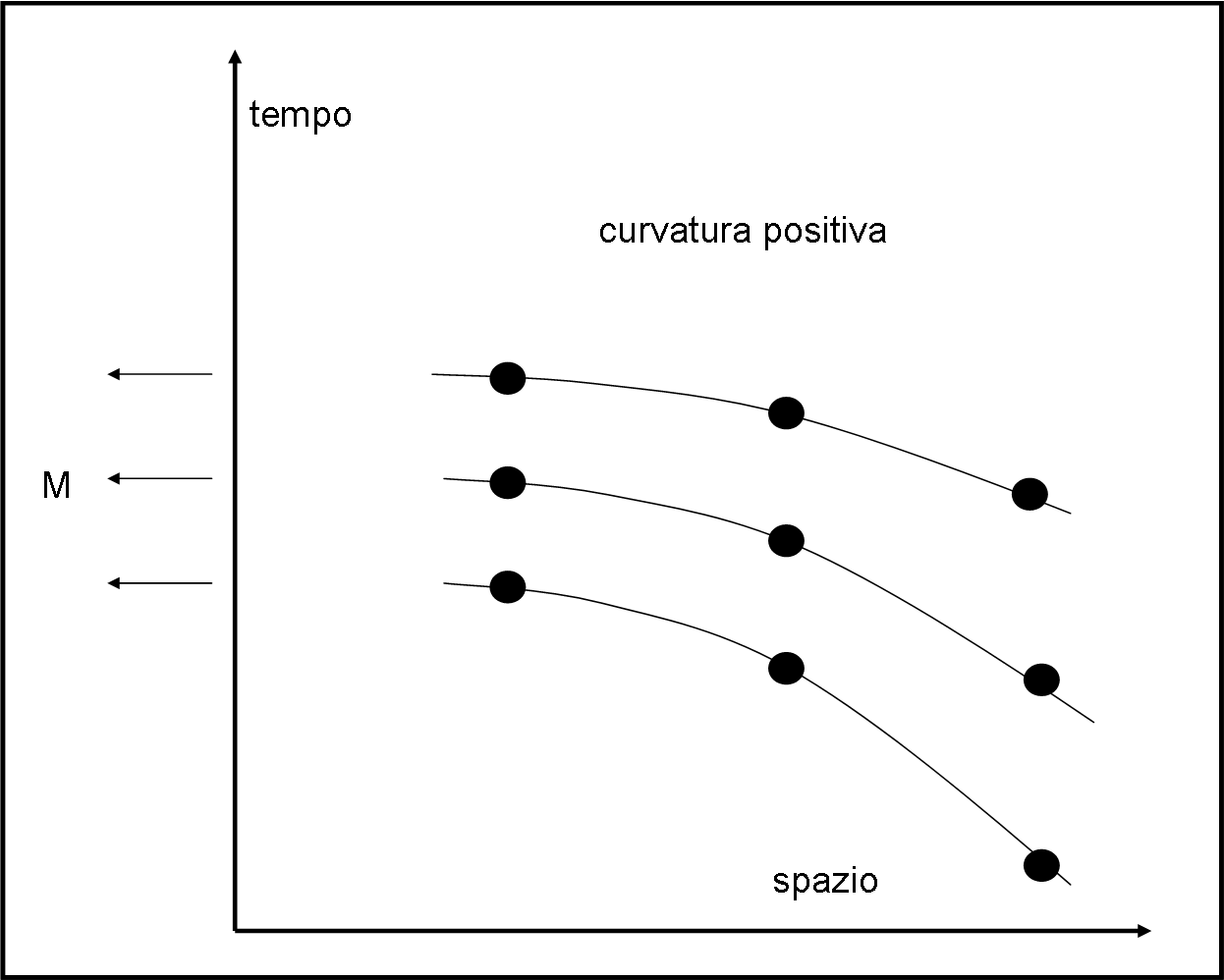
Esse hanno la stessa velocità in ogni momento, ma questa aumenta continuamente. Inoltre, la traiettoria di ognuna di esse è diretta verso il centro di massa e, quindi, si avvicinano. Se rappresentiamo le traiettorie rispetto al tempo, abbiamo le curve di Fig. 8, dove siamo di fronte a una curvatura positiva.

Per riassumere in modo banale la questione, pensiamo a uno spazio bidimensionale che giace sul piano orizzontale e due piani perpendicolari di spazio- tempo. Newton potrebbe descrivere i moti nei piani perpendicolari, mentre una semplice geometria euclidea descrivere le traiettorie sul piano orizzontale. Einstein invece deve descrivere qualsiasi traiettoria nello spaziotempo che non è certamente una media brutale delle varie curvature… Non è difficile comprendere quale ostacolo si sia trovato di fronte… Nella storia della RG vedremo come si è mosso e come anche un italiano ne sia stato coinvolto.

Fermiamoci qui, per adesso. Il prossimo passo sarà quello di unificare in modo logico e coerente gli articoli apparsi finora con la sigla “verso la RG”. Poi passeremo alla parte “storica”. Qualche approfondimento qua e là e, infine, saremo pronti per le numerosissime soluzioni e applicazioni reali della formula precedente, forse la più importante nella storia dell’astrofisica (e non solo…).

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale