Questo articolo è stato inserito nella pagina d'archivio dedicata alla Relatività Generale

 

Questo articolo “cerca” di introdurre la Relatività Generale da un punto di vista abbastanza particolare, che, però, assomiglia sicuramente al carattere fanciullesco di Einstein. Un metodo saltellante e poco logico? Beh… anche in questo senso ho cercato di avvicinarmi alla formulazione di Albert, che, in fondo, non sapeva nemmeno lui cosa cercare e come cercarla. Aveva solo grandi dubbi e qualche domanda molto semplice, semplice come l’intero Universo. Un  uomo vero, un figlio del Cosmo, forse il solo che parlando il suo stesso linguaggio, poteva superare un confine apparentemente insuperabile.

Dopo aver costruito una splendida struttura con i LEGO o con il “vecchio” MECCANO, un bambino è normalmente insoddisfatto. Superato il primo, effimero, momento di trionfo e di gioia, subentra immediatamente la domanda: “E adesso…?”. La costruzione è bella, ma è limitata. Il bimbo vorrebbe di più e subito. Non gli resta che chiedere ai genitori la scatola successiva e la conclusione è la solita frase: “Non sei mai contento!”.

Bene, Einstein si trovava sicuramente nello stesso stato d’animo dopo aver descritto la Relatività Ristretta e le sue sbalorditive applicazioni alla dinamica. In fondo non era stato così difficile… Newton era stato relegato a genio, sicuramente immenso, ma costretto a muoversi all’interno delle rigide pareti di un mondo limitato, dove la luce aveva una velocità che poteva essere considerata infinita. Di fronte ai risultati dell’elettromagnetismo Einstein non poteva che farsi una domanda quasi banale: “Perché le cose non funzionano?”.

La sua mente quasi infantile non poteva che darsi una risposta altrettanto semplice: “Perché la luce ha una velocità limitata”. In questo modo era “facile” dimostrare che nei sistemi inerziali i fenomeni fisici rimangono gli stessi. Una risposta semplice a una domanda semplice. Una risposta che può essere tradotta in: “Lo spazio e il tempo devono essere strettamente collegati tra loro”. Pensiamoci bene… lo spaziotempo non nasce da un teoria piena di formule e di teoremi matematici, ma da una semplice domanda a cui Einstein ha risposto nel modo più “ingenuo”. E’ stato poi facile applicare alla sua idea di base la trasformazione di Lorentz. Una formula matematica che diventava improvvisamente l’essenza del Cosmo. Albert ha dato vita a una “parola” di per sé fredda e rigida.

A questo punto, avendo trovato la chiave di lettura dell’Universo, attraverso un linguaggio infantile, non gli è stato difficile arrivare all’uguaglianza tra massa ed energia e alla più famosa formula della Scienza. L’applicazione al microcosmo, l’unico che sembrava obbedire alla sua rivoluzione epocale, portava con sé spiegazioni quasi banali sui decadimenti radioattivi e sulle tante proprietà della materia all’interno delle stelle e non solo. Perfino i muoni sembravano corrergli incontro per ringraziarlo di avere fatto luce sul loro mondo misterioso.

Sì, tutto grande e geniale, ma… “E adesso…?”.  In fondo aveva “solo” dimostrato che tutti fenomeni della fisica devono essere uguali nei sistemi inerziali, che spazio e tempo non sono separati, che massa ed energia sono praticamente la stessa cosa. No, non poteva bastargli… ma non sapeva nemmeno che domande farsi esattamente. Sicuramente avrebbe voluto estendere la sua relatività anche ai sistemi non inerziali.

Troppe cose sembravano vaghe e artificiose. L’importante, però, era restare bambino senza aver paura di chiedere qualcosa di più basandosi solo su formulazioni della massima semplicità. L’uovo di Colombo era sempre pronto a colpire. Ecco, forse, la dote più grande di Einstein: non aver mai avuto paura di dubitare anche delle cose più assodate e, nello stesso tempo, non aver mai avuto paura di farsi domande apparentemente banali e di rispondere in modo apparentemente ingenuo.

La grandezza di uno scienziato, capace di trasformare la visione di un Universo non ancora osservato, sta proprio nell’umiltà delle proprie domande e risposte. Prima delle formule complicate ci vogliono le idee e queste nascono, a volte, più nelle menti infantili che in quelle troppo sofisticate e artefatte.

Prima di iniziare il travagliato e fanciullesco tragitto che lo ha portato alla teoria più generale mai costruita, ricordiamo che Einstein è passato attraverso idee ed esperimenti mentali  spesso ingenui, abbozzati o addirittura errati, con tutta la passione e semplicità di cui era capace.  Questo gli ha permesso di costruire una vera opera d’arte, un qualcosa di estremamente semplice nella sua struttura, capace di risolvere, però, problemi che non si erano ancora minimamente affacciati alla conoscenza umana. Ogni suo tentativo lo ha aiutato a preparare la mente ad aprirsi alle idee risolutive che si accendevano come lampadine. Facciamo un esempio molto indicativo.

L’idea di un sistema di riferimento assoluto e la fumosità di tutte quelle forze apparenti che bisognava introdurre per spiegare lo stesso fenomeno in sistemi non inerziali non gli andava a genio. La sua mente cominciò a formulare domande semplici, quelle che corrispondevano meglio al linguaggio dell’Universo. Un problema lo assillava: la RR aveva dimostrato che non esisteva un sistema di riferimento assoluto, ma solo sistemi in moto relativo. Perché mai la stessa cosa non poteva valere per i moti accelerati?  Una semplificazione ovvia per chi pensa in modo semplice. Un moto accelerato comporta fenomeni diversi per un osservatore in stato di quiete. Perché mai moti inerziali e moti accelerati devono essere trattati diversamente? E cosa significa stato di quiete?

E fece un esempio banalissimo...

Prendiamo due pianeti liquidi posti lontano e isolati nello spazio (Fig. 1): uno ha la forma schiacciata come quello della Terra, l’altro è una sfera perfetta.

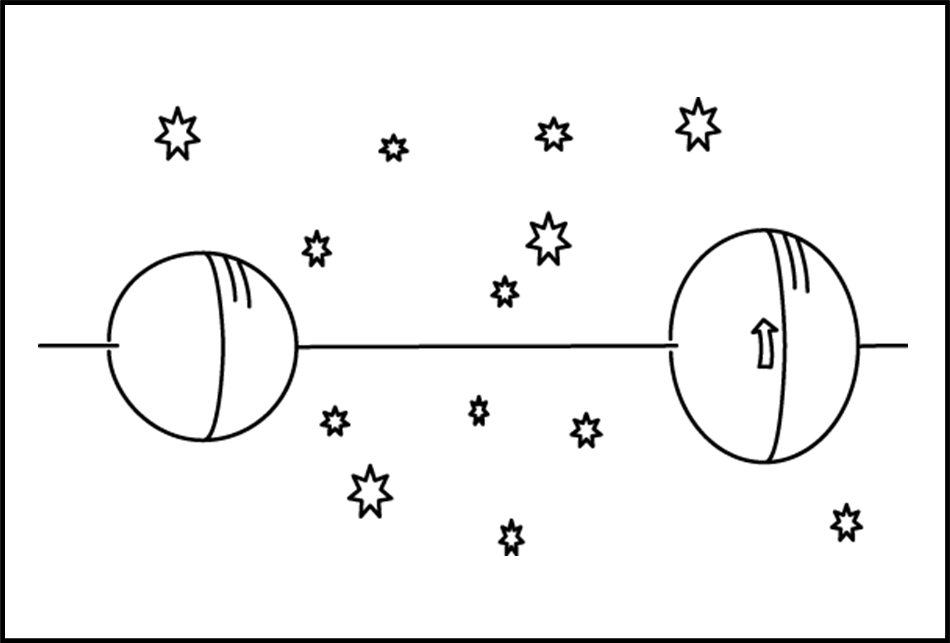
Consideriamo per loro un solo asse di rotazione. Attenzione, però, parliamo di rotazione relativa. Ossia chi sta sul pianeta sferico vede girare l’altro e viceversa. Quello allungato gira sicuramente e lo dimostra la sua forma, ma se ci portiamo su di lui anche quello sferico appare ruotare. Newton concluderebbe, però, che quello sferico non ruota rispetto a un sistema inerziale.

No, questo non piace a Einstein. Entrambi i pianeti vedono l’altro ruotare e sono entrambi isolati. Perché mai dovrebbe esistere una differenza come quella mostrata dalla sfera schiacciata? Nessuno dei due osservatori potrebbe mai dire che l’altro non ruota. In altre parole, nessuno dei due può considerarsi un osservatore privilegiato! La spiegazione di Newton “un sistema è inerziale e l’altro è soggetto alla forza centrifuga” non può essere accettabile… troppo complicata e poco armonica. Qualcos’altro deve intervenire per fare differire la forma dei due pianeti, qualcosa di OSSERVABILE.

La prima risposta che viene in mente a Einstein sono gli studi di Mach. Una soluzione non esatta, ma che lo costringe a studiare meglio la gravitazione e i suoi effetti. Nessuna paura di sbagliare se il problema viene affrontato con la massima concentrazione possibile e senza pregiudizi.

Ernst Mach pensava che le stelle, fisse oppure no, dominassero il moto non inerziale dei singoli oggetti. Le stelle, pur lontanissime, costringevano i corpi ad accelerare a causa della loro presenza fisica. Le stesse stelle, teoricamente, potevano subire  trattamento analogo da qualsiasi altro corpo fisico. Tuttavia, la grande distanza permetteva a certi moti di apparire inerziali ed altri no. Il tutto si basava sulla distribuzione delle stelle rispetto all'oggetto in questione. I moti inerziali lo erano solo apparentemente e ciò si doveva alla configurazione del moto dell'oggetto rispetto ai corpi fisici lontani, ma presenti.

Siamo ben lontani dalle conclusioni finali, ma l’idea della massa come vera dominatrice del moto dei corpi si era già affacciata. Non solo però. Aveva già iniziato a pensare che non doveva esserci nessuna vera differenza tra sistema accelerato e sistema inerziale. Entrambi erano moti relativi.

In qualche modo, Einstein vide la via da seguire: doveva distruggere ogni separazione tra moto inerziale e moto accelerato, come appariva nella sua RR. Chi sta dentro l’ascensore che cade pensa di non essere accelerato in un campo gravitazionale, chi sta fuori e non cade dice che l’uomo dentro l’ascensore sta accelerando in caduta libera. La visione dell’accelerazione diventa qualcosa di relativo.

Una serie di pensieri quasi ingenui; nessun imbarazzo a entrare in un’ottica dai risvolti poco scientifici che però lo mette di fronte a problemi nascosti; la capacità di estrarre le parti più logiche e innovative; una serie di conclusioni quasi ovvie e… la costruzione LEGO è finita! “E adesso…?”

A questo punto, va ricordata la situazione dell’astrofisica in quegli anni. Molto semplice: essa non era praticamente ancora nata e le stelle fisse non erano un pensiero da ignorante sprovveduto. Il moto dei corpi poteva essere studiato solo nel Sistema Solare e nemmeno si conosceva l’esistenza delle galassie. La loro forma a disco appiattito e l’influenza di quelle vicine avrebbe sicuramente sveltito le conclusioni  preliminari, frammentarie e disordinate, di Einstein.  Questo fa della teoria della RG un capolavoro ancora più grande: arrivare a spiegare gli oggetti più esotici dell’Universo (roba da tesi di laurea), quando si è ancora in prima elementare!

Un altro grande dubbio, insopportabile per Einstein, era l’effetto immediato insito nella teoria di Newton. Se, per una qualche ragione fosse stata spostata la massa del Sole o fosse sparito del tutto, gli effetti sulla Terra sarebbero stati immediati. Ma questo voleva dire mandare un’informazione a velocità infinita, superiore a quella della luce. E questo per Albert era impossibile. Una domanda alla portata di chiunque e una risposta che doveva essere altrettanto esauriente.

La forza a distanza non poteva, perciò, essere plausibile. L’idea che gli girò in testa fu proprio quella di una curvatura dello spaziotempo che introducesse traiettorie predefinite nelle vicinanze di una massa considerevole. Una soluzione apparentemente ovvia (o quasi) che deve la sua grandezza proprio al fatto che qualsiasi risposta era considerata da Einstein meritevole di attenzione.

Ci sarebbero moltissimi altri esempi di esercizi mentali e di dubbi (qualcuno lo citeremo). Tutti, però, sotto forma di problemi alla portata di chiunque, come formulazione. Ciò che non era alla portata di tutti era la capacità di darne una soluzione altrettanto semplice e banale. Ripetiamolo ancora: Einstein stava riuscendo a parlare con l’Universo usando il suo linguaggio, quello dell’umiltà e della semplicità assoluta.

Riassumiamo ancora una volta i punti fondamentali della RG, cercandoli di vedere sotto un aspetto quasi fanciullesco.

Non esiste effettiva differenza tra sistemi accelerati e sistemi inerziali. In particolare, un sistema inerziale non è altro che un sistema di riferimento in caduta libera che sta subendo l’accelerazione gravitazionale. Basta pensare a un ascensore a cui si è spezzata la corda o a un imbianchino che sta cadendo da un ponte. Che dire? Un esperimento (mentale) sotto gli occhi di tutti. Verrebbe da dire: “Tutto qui?”. Eppure da questa constatazione nasce il principio di equivalenza.

Lo spaziotempo non è euclideo, ma è simile a una superficie sferica o a una piastra un po’ speciale. E’ uno spazio curvo e di conseguenza i corpi immersi in esso devono seguire le traiettorie corrispondenti alla curvatura  che stanno attraversando. Dopo aver descritto la RR non è difficile stabilirle: esse sono quelle che corrispondono al tempo proprio massimo. In altre parole definiscono le geodetiche.

Una visione di una semplicità sconcertante, ben superiore a quella della forza di maga Magò-Newton. Non vi è bisogno di forze, basta solo “cadere” lasciandosi trasportare dall’andamento dello spaziotempo. Lunghezze e orologi (legati strettamente dalla RR) ci verranno dietro. Chi non ha mai usato uno scivolo dalle forme più strane per tuffarsi in piscina? Basterebbe questa esperienza per capire la curvatura dello spaziotempo.

Non resta, allora, che la parte veramente difficile, quella che ha visto Einstein diventare giocoforza un matematico e attingere senza timori agli studi più avanzati sulle curvature dello spazio: determinare come la presenza di materia e/o energia possa curvare lo spaziotempo.

La Relatività Generale, in fondo, è tutta qui.

In questo contesto, simile a un gioco di bambini, risulta particolarmente suggestiva la descrizione che lo stesso Einstein dà dello spaziotempo.

Esso deve essere pensato come un “mollusco”, un’“ameba”, composto anch’esso di materia/energia. Un corpo molle che si piega, si flette, si deforma.  Lo spazio è una componente materiale del Cosmo.  Un’entità che  si incurva e si storce. Ne segue che qualsiasi cosa viva al suo interno è costretta sia a seguirne i capricci che a modellarlo. Le masse deformano il mollusco e costringono gli oggetti a muoversi lungo le sue deformazioni.  La Terra non gira intorno al Sole perché è tirata da una misteriosa forza, ma perché sta correndo dritta in uno spazio che si curva.

Cosa meglio di uno dei tanti orologi molli di Dalì può darci un esempio concreto di questo mollusco?

 

 

Abbiamo toccato vari punti, che saranno trattati in modo ben più dettagliato in seguito. Non preoccupiamoci, quindi! Tuttavia, non stupiamoci più di tanto se la descrizione che daremo sarà molto saltellante e ci farà passare da un argomento a un altro senza nessuna apparente logica. In fondo, cercheremo solo di imitare il “bambino” Einstein che si annoia di un gioco e ne prende un altro per poi tornare al primo. La cosa poco “bambinesca” e straordinariamente geniale è il legame nascosto che lega i vari giochi. Un legame che può essere descritto solo con il linguaggio semplice dell’Universo.

Una volta capitane l’essenza, diventa quasi un esercizio da noiosi matematici rendere il tutto alla portata degli… uomini. Non per niente Feynman ebbe a dire che non era tanto la stupefacente teoria a sbalordire, quanto il pensare che a qualcuno fosse potuta venire in mente. Aveva ragione: solo a un uomo che viveva nell’Universo, senza ancora conoscerlo, ma che sapeva capire il suo linguaggio, poteva essere concesso di avvicinarsi alla realtà.

Tutto ciò che poteva essere verificato per pochissimi fenomeni osservabili è diventato un po’ alla volta la struttura portante dell’intero macrocosmo. Effetto lente, buchi neri, onde gravitazionali e mille altri oggetti o fenomeni non sono che l’ovvia conseguenza di una chiacchierata tra Albert e l’Universo. Un bimbo direbbe: “Che c’è di strano?”

Lo spazio è curvo

Abbiamo discusso a lungo di curvatura di uno spazio a due dimensioni e abbiamo visto come la geometria che lo descrive si discosti completamente da quella euclidea che impariamo a scuola. Come ormai abbiamo già capito, la curvatura di uno spazio (lasciando da parte il tempo, almeno per adesso) è legata strettamente alla Relatività Generale. Vale, perciò, la pena di capire ancora meglio cosa si intenda per “curvatura”

Ho letto varie “divulgazioni” della relatività ristretta e di quella generale che tutto fanno fuorché spiegare, anzi inducono errori fondamentali che poi sono difficili da estirpare. Questo è il motivo per cui voglio preparare per bene l’argomento degli argomenti, quello su cui si basa gran parte della astrofisica macroscopica, non ultima la creazione delle onde gravitazionali.

Accettiamo, quindi, alcuni articoli che sembrano distanti dal nocciolo del problema e che, invece, preparano la mente ad affrontare certe conclusioni che solo un genio poteva non solo descrivere, ma anche solo immaginare.

Questa volta parliamo di una “falsa” curvatura, ossia dimostriamo come certe caratteristiche che abbiamo compreso con qualche difficoltà su una superficie sferica, possano essere riprodotte perfettamente su una superficie piana, agendo su altre caratteristiche fisiche.

Lo scopo è quello di far capire che parlare di curvatura dello spaziotempo non è un qualcosa che debba subito far pensare a una superficie o addirittura a uno spazio realmente curvo, ma solo a un qualcosa che permetta di considerare come linea di minima distanza (geodetica) una traiettoria non rettilinea. Insomma c’è curvatura e curvatura, ma non facciamoci ingannare dalla “parola” in sé e pensiamo al concetto ben più generale.

Non commettiamo lo stesso errore che si fa parlando di forma dell’Universo, immaginandosi veramente una struttura con una forma a sfera, a sella o completamente piatta. Quello che conta è la geometria che descrive un qualcosa e nel caso della curvatura legata alla Relatività Generale una geometria del tutto identica a quella esistente su una superficie sferica, ma senza per forza pensare a una vera superficie curva…

Spero di aver chiarito le idee e non di averle confuse. Meglio passare a un esempio che, guarda caso, ho -ancora una volta- sviluppato rifacendomi a quel pozzo di scienza divulgativa che è Feynman.

Dimentichiamoci, perciò, la superficie sferica (tenendo ben presente però le conclusioni che abbiamo ricavato) e mettiamoci su un piano che più piano non si può. Un  piano apparentemente piano, ma in cui le condizioni fisiche sono ben diverse!

Prendiamo un punto qualsiasi del piano. Diamo sufficiente spazio attorno al punto in tutte le direzioni (consideriamolo pure al centro, anche se parlare di centro di un qualcosa di indefinito spazialmente è sempre privo di senso). Adesso, immaginiamo che il nostro piano diventi una specie di piastra per cuocere i cibi, però … al contrario. Mi spiego meglio. Il punto centrale è quello in cui la temperatura è minima, mentre a mano a mano che ci allontaniamo, la temperatura sale con una certa legge, che, al momento ci interessa ben poco.

Possiamo anche pensare che uno spazio piatto, veramente piatto a prima vista, abbia una certa capacità di far variare la “temperatura” a distanze crescenti da un certo punto, che possiamo identificare con un oggetto dotato di una certa massa. Una massa capace, in qualche modo, di fornire calore tutt’attorno. Una specie di fornello al contrario. Il calore è, però, solo un esempio. L’importante è che causi una qualche legge che agisca sullo spazio circostante e sui suoi strumenti di misura.

Fatemi disegnare la Fig. 2 che riesce sicuramente a spiegare la faccenda meglio che tante parole. Ogni cerchio attorno al punto-massa -o quello che volete- ha una temperatura crescente verso l’esterno. Per misurare le distanze su questa strana “piastra”, dobbiamo usare un righello di distanza unitaria (sappiamo quanto importanti siano i righelli della relatività ristretta… QUI, Fig. 14).

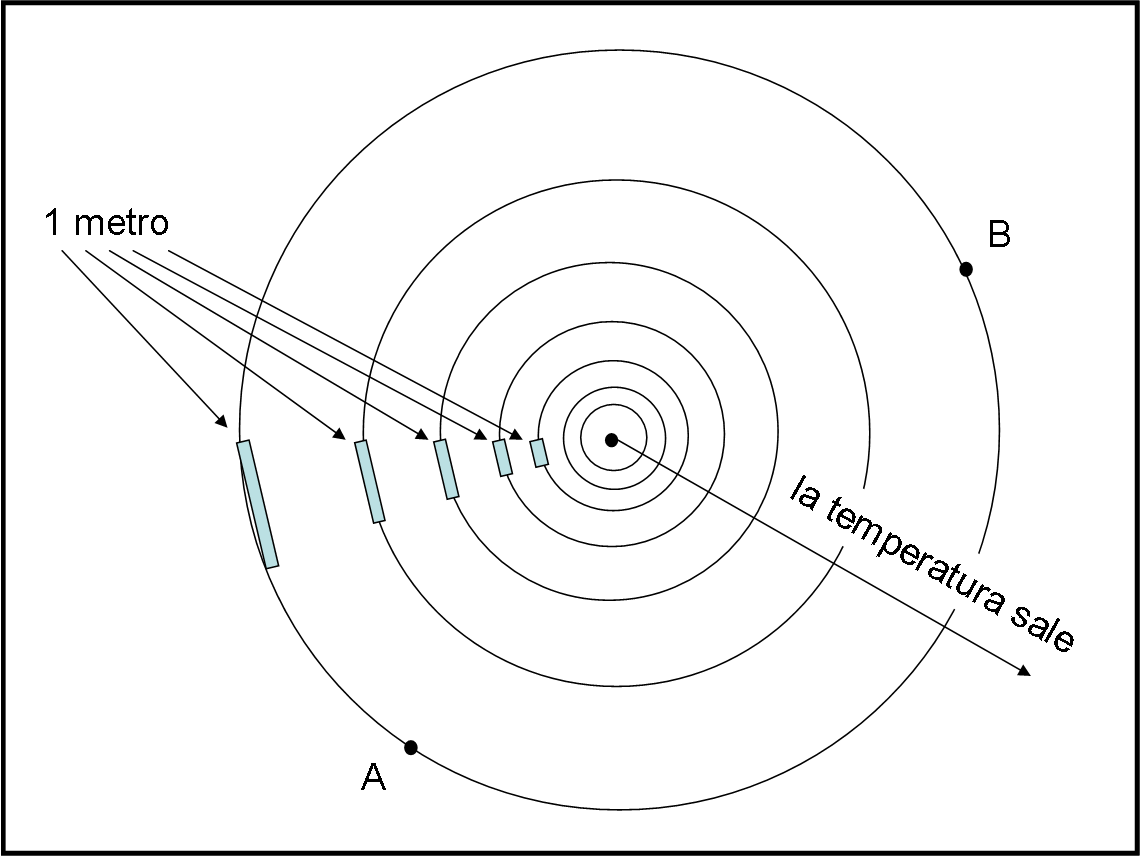
Purtroppo, però, il materiale di cui è composto il righello è sensibile alla temperatura e le sue dimensioni si dilatano in funzione di essa. Il che vuole anche dire che qualsiasi oggetto di quel materiale venga posto sulla piastra è costretto a dilatarsi seguendo le regole del gioco. Ricordiamo sempre bene che la dilatazione o contrazione non è la stessa da punto a punto, ma è funzione della distanza dal centro.

Nella figura, sulla sinistra, abbiamo disegnato i righelli unitari relativi a varie temperature crescenti dal centro verso l’esterno. Attenzione: li abbiamo disegnati, ma verranno tolti quando si passerà alla prova vera e propria.

Immaginiamoci adesso una scuola aliena, dove si stanno interrogando alcuni studenti. E’ una prova impegnativa, estremamente importante per il futuro scolastico. Ciò che si deve fare è andare su quello strano mondo, che gli studenti non conoscono, ed eseguire una certa misura con un righello di misura unitaria (un metro). Viene mandato per primo uno studente abbastanza “normale”.  Il giovane non è “piatto” e vede, perciò, chiaramente che il mondo raggiunto è veramente piatto anche estrinsecamente. Purtroppo, gli alieni non possono sentire il caldo e il freddo, dato che questo senso non fa parte della loro dotazione sensoriale… Tuttavia, sono “fatti” dello stesso materiale dei righelli che hanno a disposizione. Nel loro mondo la temperatura è sempre perfettamente costante…

Il compito che gli è stato dato è quello di trovare la minima distanza tra due punti A e B. “Banale!” pensa lo studente. Lo spazio è piano e non deve fare altro che prendere il suo righello e vedere quante volte è contenuto nel segmento AB. Geometricamente non ha sbagliato niente, tranne il non aver tenuto conto dell’espansione o della contrazione del suo righello (che non può notare dato che anche lui -il piccolo alieno- è fatto dello stesso materiale del righello).

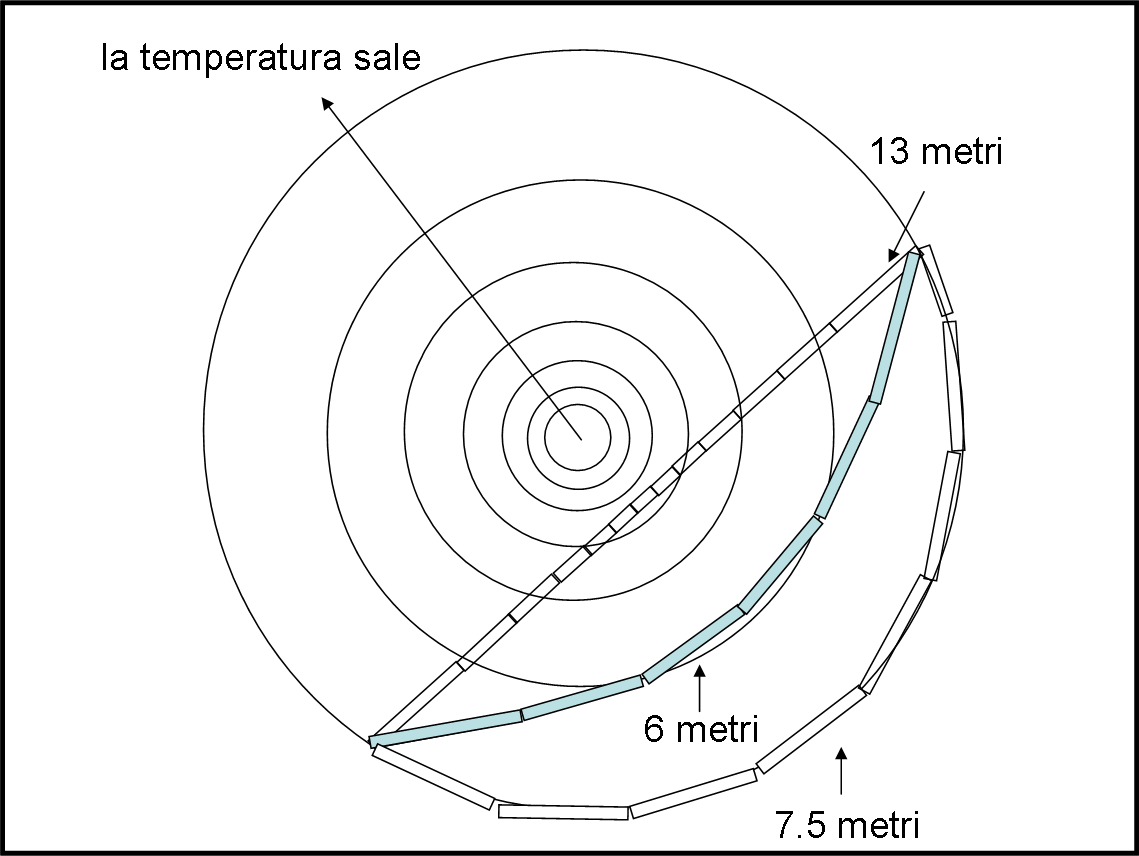
Tracciamo il segmento AB nella Fig. 3.

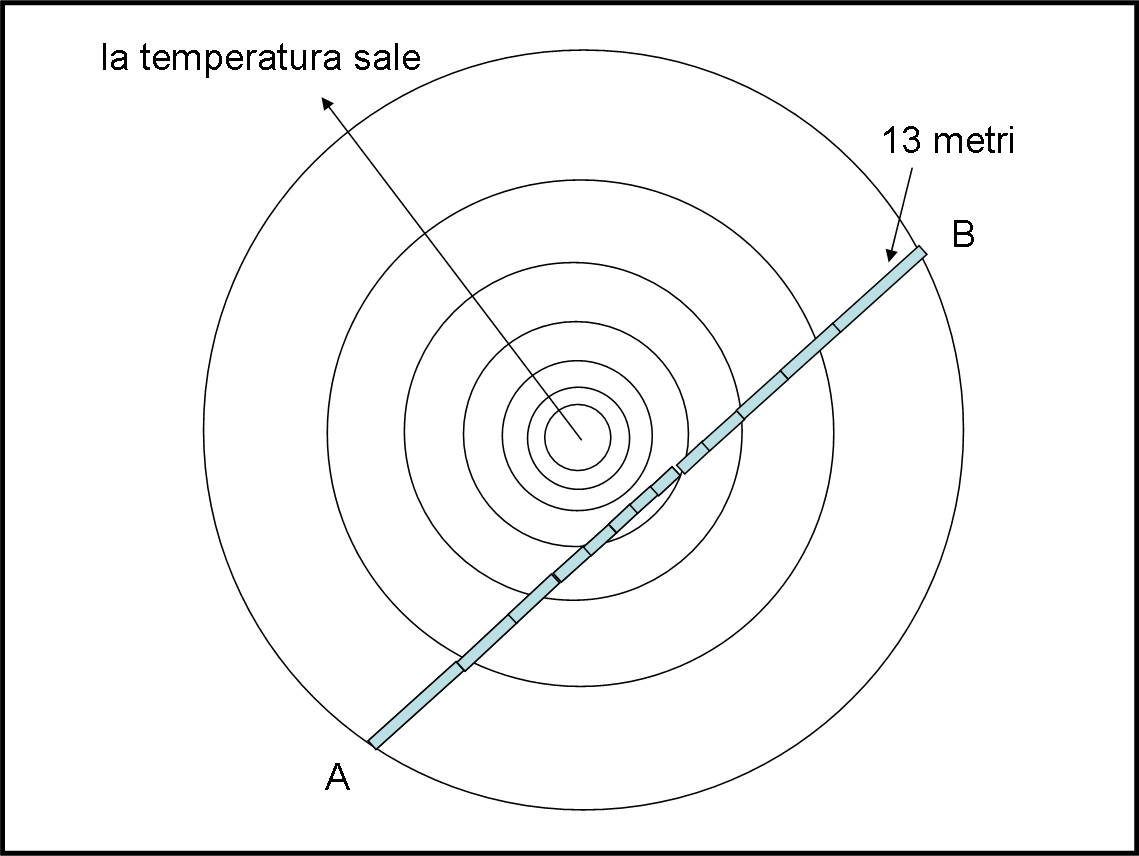
Si vede chiaramente che il segmento attraversa cerchi concentrici con temperatura sempre inferiore fino a un minimo e poi ricomincia a tornare verso zone a temperature più alte. Per metterlo in maggiore difficoltà A e B sono stati scelti alla stessa distanza dal centro, in modo che la temperatura di partenza sia uguale alla temperatura di arrivo.

Mentre il nostro amico sistema il righello, la lunghezza di quest’ultimo diminuisce fino a raggiungere un valore minimo dove la temperatura è più bassa e poi ricomincia a salire fino a tornare alle identiche dimensioni della partenza. In questo modo anche un osservatore esterno (amico dello studente) potrebbe misurare il righello all’inizio e alla fine e potrebbe dire che nulla è cambiato. Povero studente e povero amico controllore…

Torna al suo mondo dando come distanza minima un valore del tutto sbagliato! Lui dice con grande sicurezza: “La minima distanza tra A e B è 13 metri. Il mio righello è stato contenuto esattamente tredici volte tra A e B”. E viene bocciato!

La Fig. 3 illustra cosa è realmente successo. Il righello varia la sua lunghezza in base alla temperatura e, a mano a mano che lo studente misura, il suo strumento si fa più piccolo per poi aumentare di nuovo. 13 metri è una distanza enormemente più grande della realtà di quello strano mondo.

La Fig. 4 illustra un altro tentativo fatto da un compagno ritenuto il migliore della classe (un vero sgobbone, senza troppo intuito, però).

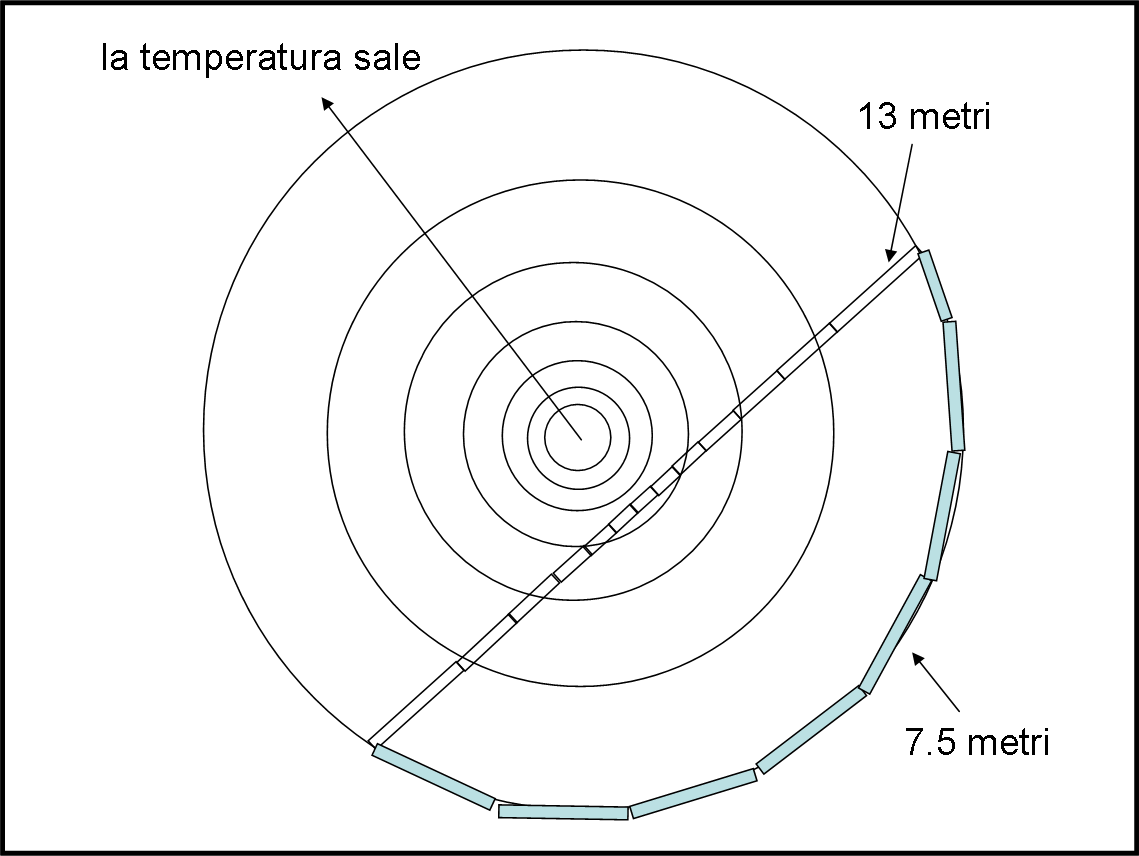
Lui sa tutto sui cerchi massimi di una superficie sferica, però non capisce che cosa c’entrano con un piano visto come tale anche in modo estrinseco. Tuttavia, è abituato a lavorare un po’ alla “io speriamo che me la cavo”, anche senza sapere il perché. Inizia a mettere i righelli lungo la circonferenza che passa da A e da B e, in realtà, trova una distanza nettamente minore: 7.5 metri!

Tutto contento torna a scuola, ma, questa volta, è costretto a subire una delusione: sì, il suo valore e migliore di quello del primo studente, ma non è ancora quello giusto.

Un terzo studente ci ragiona sopra e trova del tutto inconcludente seguire una circonferenza che non sarebbe né carne né pesce.  Valutando i risultati di chi l’ha preceduto, ha un lampo di genio (lui è abituato a queste intuizioni, ma la scuola è rigida e preferisce che si seguano regole ben stabilite senza dare molto spazio alla fantasia, anche se basata su una logica ineccepibile).

Fa qualche calcolo e capisce che il percorso minimo dipende sia dalla distanza percorsa in modo rettilineo (il piano resta un piano), ma anche dalla distanza dal centro. Se passasse troppo vicino a questo il numero di righelli da usare aumenterebbe troppo (vincerebbe la contrazione). Se andasse oltre la circonferenza di A e B, guadagnerebbe in termini di lunghezza del righello, ma perderebbe in distanza lineare. Ci vuole un giusto compromesso.

Ancora qualche calcoletto e poi alza la mano, proponendosi per un nuovo tentativo. I professori si guardano tra loro, alquanto dubbiosi, però non possono negargli la prova. Il terzo studente scende sullo strano mondo piatto e segue una traiettoria sicuramente curva ma che dona un risultato di soli 6 metri, come mostra la Fig. 4.

La sua gioia si ingigantisce (come il righello) mentre guarda  la bocca aperta dei professori che, d’ora in poi, lo vedranno con occhi diversi.

In poche parole, la legge con cui il righello si allunga con la temperatura è una proprietà fondamentale di quel mondo piatto e impone un percorso di minima distanza, che tutto è fuorché una linea conforme all’aspetto geometrico apparente. Una proprietà che viene evidenziata dalla presenza della massa-piastra.

La morale della storia è che una massa dotata di proprietà “speciali” (la stessa massa, in realtà) è capace di deformare lo spazio intorno a lei in modo che le distanze minime non siano più linee.

Tradotto in parole ancora più semplici ed esplicative: una massa è capace di variare la lunghezza dei righelli a seconda della loro distanza rispetto a lei. Sappiamo, però, che lo spazio è in pratica un qualcosa definito dai righelli (ricordatevi lo studente Einstein durante il suo confronto con lo studente Newton… QUI, Fig. 14). In conclusione: una massa è capace di deformare lo spazio, dove per deformare si intende qualcosa di ben più generale che la curvatura di una superficie sferica. In questo contesto, la minima distanza segue regole del tutto particolari.

Uno spazio curvo a tre dimensioni

Questo articolo non contiene praticamente formule, ma è decisamente FONDAMENTALE per capire l’essenza più profonda della RG e della sua definizione di spazio tridimensionale curvo. Non perdetelo e non esitate a porre domande se vi rimane qualche dubbio. Capirete anche perché abbiamo perso tanto tempo a spiegare le regole geometriche di una superficie sferica (QUI), confrontandole con quelle euclidee e anche perché abbiamo scaldato un piano con una strana piastra. Sembrerà una trattazione addirittura pedante, ma il concetto di curvatura è troppo importante per rischiare di non chiarirlo completamente.

Prima di cominciare è necessario capire un concetto veramente base. Quando abbiamo detto che viviamo in un mondo, la Terra, che non è euclideo, ci siamo limitati alla superficie sferica della Terra, ossia a una curvatura bidimensionale. Adesso faremo un  passo decisamente più importante e decisivo, cercando di valutare se lo spazio a tre dimensioni che contiene la Terra è uno spazio curvo oppure no. Non andate avanti se non avete capito questo punto. Chiedete senza paura e cercheremo di spiegarlo ancora meglio. Tralasciandone una giusta comprensione, tutta la RG diventerebbe un ostacolo insormontabile e privo di senso…

Abbiamo visto che una superficie curva può essere simulata perfettamente da un piano con una strana piastra che scalda sempre di più allontanandosi dal suo centro. Il calore deforma il righello che serve per misurare le distanze e se viviamo su quel piano la linea di minima distanza è una curva e non una retta. In qualche modo, abbiamo capito che il concetto di curvatura non è essenzialmente dovuto a una superficie realmente “curva” (come la intendiamo noi) ma a un comportamento ben più generale.

Capito questo concetto, possiamo tornare a disegnare una superficie curva attraverso una sfera, dato che le sue stranezze sono molto più semplici da raffigurare. Tuttavia, non dimentichiamoci che è solo un modo comodo per rappresentare la situazione che potrebbe anche essere ottenuta su un piano perfetto, attraverso altre manipolazioni. Piastra che scalda e superficie curva si comportano nello stesso identico modo.

L’importante è che la situazione sia comprensibile da un personaggio che vive nello spazio e ha anch’esso le stesse dimensioni del suo spazio e non attraverso una visione che sfrutta una dimensione supplementare. In altre parole stiamo parlando di curvature intrinseche e non estrinseche. D’altra parte, se questo “furbo” espediente può essere risolutivo per uno spazio a due dimensioni, diventa impraticabile per uno spazio a tre dimensioni (vi sfido a guardarlo in uno spazio con una dimensione in più!). Dobbiamo, perciò, abituarci ad accorgerci di  una “curvatura”del proprio spazio, senza sperare di vederla in modo estrinseco.

Un compito non certo facile, soprattutto da un punto di vista concettuale e intuitivo. Bisogna munirsi di grande immaginazione e riuscire a non essere troppo influenzati dall’aspetto grafico.

Qual è il problema più grande? Sicuramente la confusione che si fa tra sfera sulla cui superficie si disegna uno spazio curvo a due dimensioni e lo spazio a tre dimensioni, contenente una sfera di una certa massa, di cui si vuole misurare o, almeno, scoprire l’eventuale curvatura. In altre parole, lo spazio in cui sta una sfera può essere curvo oppure no, ma di certo non lo indica la forma della sfera che è parte integrante dello spazio. Siamo in balia della visione intrinseca senza nessun aiuto da parte di utili spostamenti in una quarta dimensione.

La forma sferica viene spesso usata solo perché è una figura simmetrica attraverso cui si può determinare la curvatura media dello spazio di cui fa parte. Se poi i pianeti o le stelle sono proprio sfere… tanto meglio!

Stiamo parlando di curvatura che può essere determinata attraverso misure eseguite solo localmente. Questo è quello che Einstein intende per spazio curvo. Ciò che si deve riuscire a fare è, quindi, rendersi conto che, almeno localmente, lo spazio in cui viviamo è curvo. Sarà poi fondamentale capire la causa di tutto ciò… Per colpa di una piastra che allunga i righelli nelle tre dimensioni o per colpa di ciò che definiamo massa (e, quindi, energia)?

Un altro punto importantissimo è che il personaggio che deve risolvere la questione deve essere intelligente e deve avere studiato molto. Lui conosce perfettamente le regole di Euclide e sa, quindi, riconoscere subito se vi è curvatura del suo spazio oppure no.

Facciamo ancora un paio di esempi nelle due dimensioni e poi affrontiamo con cautela le tre dimensioni…

Immaginiamo il nostro studente della volta scorsa, che su una superficie estrinsecamente curva o riscaldata in qualche modo, voglia muoversi per ottenere un quadrato. Parte da un punto e segue tratti di uguale distanza (per lui) piegando al momento giusto di 90°. Per quanto detto precedentemente (e lo potete provare direttamente), in entrambi i casi, alla fine del percorso, non si trova sicuramente nel punto di partenza.

Lui non ha tracciato una figura intrinsecamente curva, dato che ha seguito le regole di Euclide (retta, angolo 90°, retta, angolo 90°,…), tuttavia alla fine il risultato non è conforme a quello previsto. Risultato: si accorge che il suo spazio non è euclideo, ossia è curvo. Ripetiamo: si accorge di vivere in uno spazio curvo dato che una figura che non è curva nel suo mondo dà luogo a un risultato non conforme a quanto previsto da Euclide.

Facciamo un secondo esempio ancora più calzante per il proseguo della trattazione. Lo studente prende una corda e la fissa in punto P qualsiasi (Fig. 5).

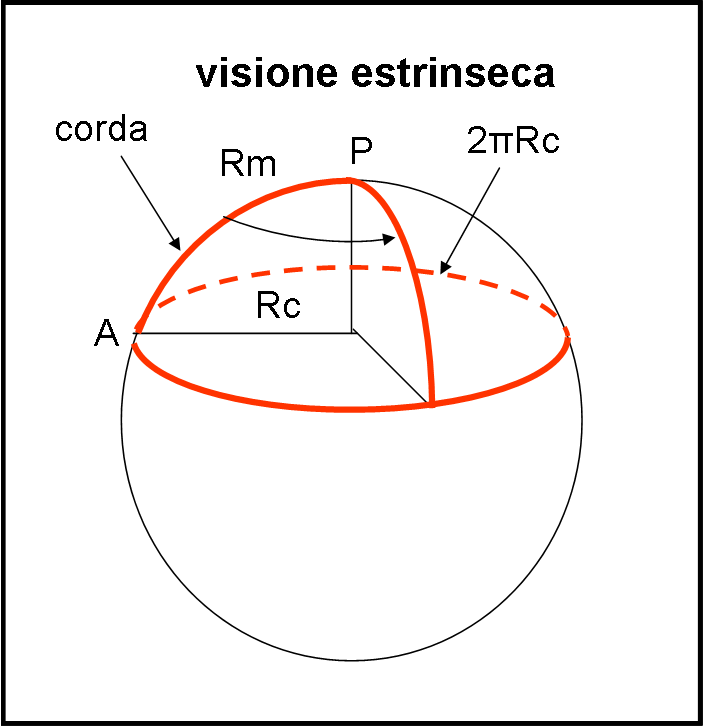
Poi si sposta fino al punto A, in modo che la corda sia ben tesa. In altre parole, ha percorso il tratto, per lui rettilineo, Rm. Comincia a camminare, mantenendo sempre la corda ben tesa. Alla fine si ritroverà nel punto di partenza A (come è capitato al piccolo riccio che abbiamo conosciuto QUI).

Nuovamente, la stessa cosa capita sia sulla superficie sferica che sul piano riscaldato (basta fissare la corda nel centro della piastra). Può concludere che NON è su uno spazio curvo? Assolutamente no. Lui ha solo scoperto di avere descritto una circonferenza di raggio Rm. In altre parole, lui ha effettivamente disegnato una curva intrinseca, che non lo stupisce di certo e non contraddice assolutamente Euclide (anche nel piano una circonferenza si traccia nello stesso identico modo!).

A questo punto, però, oltre che a misurare il raggio Rm (la corda), può anche misurare la circonferenza che ha descritto. La chiama C. Notiamo bene che mentre la circonferenza C può essere misurata direttamente (curva intrinseca), non lo è di certo la distanza Rc che è completamente fuori dallo spazio in cui vive. La vediamo noi perché abbiamo aggiunto una dimensione... Lui può solo calcolarlo utilizzando Euclide.

Infatti, conoscendo Euclide, sa benissimo che il rapporto tra circonferenza e raggio è dato da un numero “fatato”, uguale a circa 6.28… (2π). Non gli rimane che dividere il suo valore di C per 6.28 e dovrebbe aspettarsi di trovare il raggio misurato Rm. Pensate che lo trovi? Nemmeno per sogno. Lui trova un numero più piccolo del suo, Rc (raggio calcolato). In formula matematica:

Rm  > Rc = C/2π

Ossia:

Rm – Rc = dR

Essendo istruito, non si spaventa più di tanto e conclude che il suo mondo a due dimensioni è CURVO, senza preoccuparsi troppo a cosa sia dovuta la curvatura. La sua curva intrinseca (circonferenza) non risponde ai principi di Euclide, dato che il raggio è più lungo del previsto. Non è la circonferenza “curva” che ha tracciato a fargli capire qualcosa, ma le sue caratteristiche confrontate con quelle della geometria euclidea. Tutto chiaro? Se non lo fosse, bloccatemi!

Fino a qui, penso che i problemi concettuali si riescano a inquadrare molto bene attraverso le figure corrispondenti. Figure che utilizzano, però, la terza dimensione. Ci piace vincere facile… Potremmo dire: basta guardare le cose dal di fuori e si vede benissimo che quello strano mondo è curvo, senza bisogno di fare tante misure…

Adesso, dobbiamo fare il passo più difficile: entrare nello spazio a tre dimensioni, in cui diventiamo personaggi obbligati a decidere se esso è euclideo oppure è curvo, vivendo al suo interno e senza nessuna figura con una dimensione in più che ci possa illuminare. Vincere non è più così facile…

La faccenda non è “matematicamente” semplice -anzi- ma a noi basta afferrare il concetto di base.

Innanzitutto, non abbiamo più una direzione particolare in cui introdurre un’eventuale curvatura. Essa può esistere in tutte le direzioni. Mi spiego meglio. Potremmo disegnare un triangolo e guardare se la somma dei suoi angoli è 180°. Oppure disegnare una circonferenza e vedere se il suo raggio è quello che ci si aspetterebbe da una geometria euclidea. O disegnare un quadrato e vedere se si chiude. Staremmo comunque valutando la curvatura in una sola direzione. Cosa succederebbe se il triangolo fosse ruotato o si cambiasse il piano della circonferenza?

La curvatura in tre dimensioni presenta componenti di curvatura che possono essere anche diverse. In parole più semplici, se trovassimo un eccesso di curvatura in una circonferenza, potremmo non trovarla o trovarla completamente diversa, ruotando la nostra circonferenza di 90° (questo è uno dei motivi che fa della formula finale della RG qualcosa di estremamente complicato da risolvere).

Soffermiamoci su questo esempio, quello più facile da comprendere. Attenzione al ragionamento da fare, evitando le confusioni con lo spazio a due dimensioni.

Teoricamente, potremmo far girare la circonferenza, variando regolarmente l’angolo tra i due piani, e vedere che curvatura ha di volta in volta. Tuttavia, c’è un metodo più semplice. Perché non considerare una sfera e agire su di lei in modo “globale”?

Innanzitutto, definiamo la sfera in questo spazio a tre dimensioni: essa è il luogo di tutti i punti che abbiano la stessa distanza da un punto detto centro. Attenzione: stiamo facendo la costruzione basandoci sul nostro metodo di misura delle distanze. In modo del tutto analogo a quando abbiamo disegnato una circonferenza su una superficie sferica a due dimensioni con una corda che per noi era la minima distanza.  In quel caso era stato facile vedere la situazione in modo estrinseco.

Questa volta NON possiamo più usare quella verifica e dobbiamo solo fidarci della conoscenza delle regole euclidee.

Dividiamo allora la superficie sferica così costruita (ossia attraverso una corda sempre uguale) in tanti quadratini infinitesimi e sommiamo le loro aree (Fig. 6).

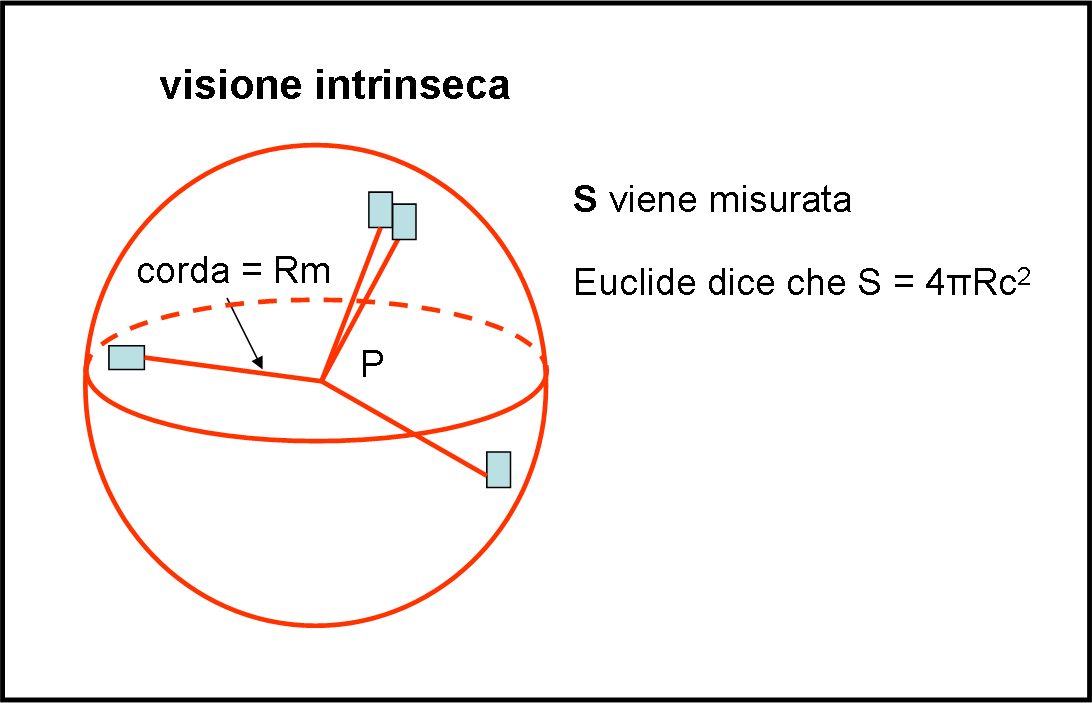
Così come avevamo misurato, precedentemente, la circonferenza costruita con la corda, adesso possiamo misurare la superficie sferica costruita con una corda del tutto simile di lunghezza Rm, libera di muoversi in tutte le direzioni dello spazio a tre dimensioni, dove stiamo vivendo.

Ribadiamo ancora: disegnando la sfera abbiamo disegnato una "curva" intrinseca nello spazio a tre dimensioni, così come avevamo disegnato una circonferenza nello spazio a due dimensioni. Non è la sfera a dirci se lo spazio è curvo, così come non era la circonferenza a dirci se lo spazio bidimensionale era curvo. Tutti d’accoro? Bene, allora possiamo proseguire…

Noi siamo istruiti e sappiamo perfettamente che Euclide dice che la superficie sferica è data da S = 4πR². Ne segue che possiamo facilmente determinare il raggio previsto da Euclide:

Rc = (S/4π)^1/2

Non ci resta che confrontare questo raggio con quello misurato, che ci è servito a costruire la sfera. Se troviamo un eccesso di raggio dR, ossia se:

Rm – Rc = dR

possiamo VERAMENTE concludere che viviamo in uno spazio tridimensionale curvo.

Ribadiamo ancora la differenza fondamentale tra i sue spazi. Nel primo, a due dimensioni, che avevamo rappresentato (vedendolo dalla terza dimensione) come una superficie sferica o come un piano riscaldato da una piastra, avevamo disegnato una circonferenza; nel secondo, che non possiamo rappresentare estrinsecamente, abbiamo disegnato una sfera. Il confronto va fatto tra la circonferenza e la sfera intese come entità geometriche intrinsecamente curve, relative a due spazi di dimensioni diverse.

Qualsiasi sia il raggio della sfera, così come qualsiasi sia il raggio della circonferenza, il problema della curvatura è esattamente la stesso. Ciò che conta è la differenza, se esiste, tra il raggio calcolato a partire dalla superficie sferica (calcolato SOLO attraverso Euclide) o dalla circonferenza (calcolato attraverso Euclide o attraverso una figura con una dimensione in più) e il raggio misurato nello spazio in cui si vive, ossia la corda usata per la costruzione della figura.

A costo di essere pedante: la curvatura dello spazio a tre dimensioni, contenente una sfera, non dipende assolutamente dal raggio della sfera, ma dal confronto tra raggio misurato direttamente e raggio calcolato con Euclide.

Tutto chiaro? Bene, anzi benissimo. Anche se non sembra, abbiamo fatto un gran bel lavoro e il concetto reale di curvatura di uno spazio non ha più problemi.

Tuttavia, matematicamente, siamo ancora lontani da una definizione accurata di spazio curvo. Noi, infatti, abbiamo trovato una curvatura MEDIA. Conoscendo solo l’eccesso medio abbiamo solo una vaga idea della effettiva curvatura di una parte del nostro spazio, ossia di quella in cui è contenuta la sfera.

Ribadiamo ancora: la circonferenza bidimensionale descriveva una parte dell’intero spazio bidimensionale, in modo perfetto. La sfera, di cui abbiamo determinato la curvatura media nelle tre dimensioni, ci indica, molto rozzamente, la curvatura di una piccola parte dell’intero spazio tridimensionale.

Diciamo subito che, per definire accuratamente la vera curvatura locale, sarebbero necessari ben sei parametri di curvatura. E già possiamo capire perché le formule finali della Relatività Generale diventano piuttosto complicate: sei numeri per ogni curvatura locale e le varie formule che li legano ad altre grandezze.  Per adesso (e per noi), la curvatura media basta e avanza…

La grande domanda che vogliamo farci, pur con le sue limitazioni, è: “Siamo in grado di dire se il nostro spazio è mediamente curvo oppure no?”. La risposta è SI e il risultato ricorda forse molto di più il caso della piastra che non quello di una superficie sferica. Non ve l’aspettavate, vero? E, invece, tra poco, concorderete con me…

Purtroppo, una misura della Terra, intesa come spazio tridimensionale, sembrerebbe portare a un risultato negativo, ma la faccenda non deve stupire se affrontiamo di petto il motivo di uno spazio tridimensionale curvo. Le misure non sono abbastanza accurate per valutare un eventuale “eccesso” nel raggio.

E qui entra in ballo Einstein che, attraverso la sua teoria, ci permette di capire perché è così difficile calcolare la curvatura dovuta alla Terra. Facendo conti piuttosto impegnativi è stato in grado di dire che lo spazio è curvo, ma che la Terra è un’attrice di scarso rilievo, una comparsa....

Il succo del discorso è questo: se esiste un luogo dello spazio che contiene una massa M e noi immaginiamo di concentrala in una sfera così piccola (e densa) tale da poter ammettere che la sua densità si possa considerare costante, allora esiste un eccesso di raggio dR che può essere scritto come:

dR= Rm – Rc = Rm – (S/4π)^1/2 = (G/3c²)M

Risulta immediatamente chiaro che l’unica variabile è la massa contenuta all’interno (il resto è una costante). La formula precedente viene detta la legge di Einstein per la curvatura media dello spazio tridimensionale. Notiamo subito che nella costante compare la velocità della luce e la costante di gravitazione. Il “profumo” è già quello di un cambiamento epocale…

Passiamo subito a un caso pratico, inserendo i valori conosciuti per le costanti G e c e per la massa della Terra (considerata di densità costante). Otteniamo:

dR(Terra) = 1.5 mm

Una cosa ridicola (ecco perché sarebbe impossibile calcolarlo direttamente), ma tale da poter dire che lo spazio tridimensionale in cui viviamo localmente è curvo per effetto della sola massa della Terra.

E se facessimo la stessa cosa per il Sole? Beh… il risultato sarebbe più significativo, anche se sempre minimo:

dR(Sole) = 0.5 km

E’ chiaro che, per sentirsi realmente preda di uno spazio “curvo” , sono necessarie masse ben più grandi. E più la massa viene compressa in un volume piccolo (ossia aumentando la densità) è maggiore è l’effetto locale, potendo arrivare più vicino alla zona “critica”.

Già capiamo però che, allontanandosi dalle masse, la trattazione assomiglia sempre più al caso trattato nella Relatività Ristretta. Ancora una volta possiamo dire che la Relatività Generale diventa fondamentale in punti particolari dello spazio, dove esistono masse significative, altrimenti Minkowski è più che sufficiente. La Relatività Ristretta è chiaramente un caso particolare (anche se molto comune) della Relatività Generale.

E’ abbastanza ovvio interpretare il risultato ottenuto precedentemente, grazie al genio di Einstein, come estremamente simile a quello della piastra… La piastra tridimensionale diventa la massa e più vicino si riesce ad arrivare più il regolo cambia di lunghezza. In parole povere, le masse riescono a cambiare l’unità di misura dello spazio, a mano a mano che ci avviciniamo a loro.

L’effetto che si riscontra è del tutto simile a quello di uno spazio curvo e la massa prende il significato di “motore” capace di rendere non euclideo lo spazio circostante. Le traiettorie di minimo percorso non sono più intrinsecamente rette euclidee, ma archi di curva e via dicendo. Curve che non sono visibili estrinsecamente (non possiamo, infatti, aggiungere una dimensione), ma che si “scoprono” confrontando la geometria spaziale con quella euclidea.

Attenzione, però… si potrebbe anche continuare in questa trattazione relativamente semplice, ma ci saremmo dimenticati di un dato di fatto fondamentale che Newton non aveva considerato: lo spazio e il tempo sono profondamente legati (le trasformazioni di Lorentz insegnano …) e, quindi, questo gioco di deformazione spaziale è costretta a diventare una deformazione spazio-temporale, con tutte le complicazioni del caso.

Non è ancora ora di occuparci del tempo e limitiamoci a pensare al fatto che se considerassimo uno spazio sufficientemente grande, al suo interno sarebbero sicuramente collocate delle masse di tutte le dimensioni. Al di là del loro effetto locale, l’insieme di tutte queste masse, inserite un po’ casualmente, ma con una certa regolarità, potrebbe dar luogo a uno spazio generale (ossia che le contenga tutte) curvo? Tante piccole piastre possono creare una specie di piastra unica su grande scala?

Per rispondere in modo “osservativo”, l’ideale sarebbe poter prendere una sfera enorme (ricordiamoci che prendiamo una sfera perché ci regala un modo semplice per valutare la sua eventuale curvatura spaziale), composta da galassie poste alla stessa distanza e cercare di confrontare la distanza misurata e quella prevista, utilizzando le regole euclidee, così come abbiamo fatto per la Terra.

In questo modo, potremmo sapere se lo spazio nel suo insieme (potremmo già chiamarlo un pezzo significativo di Universo ), in cui sono contenute masse in modo più o meno omogeneo, sia uno spazio euclideo oppure curvo. In altre parole, piatto oppure no. Come vediamo molto bene, ci avviciniamo a quella che viene chiamata “forma” dell’Universo (della quale abbiamo parlato QUI).

Molti sono stati i tentativi in tal senso, ma la risposta è ancora molto aleatoria, anche se si pensa sempre di più a uno spazio piatto (quello teoricamente più probabile, oltre che avvalorato da osservazioni indirette), che non lede comunque la curvatura locale nei pressi di ogni singola massa.

Bene… tanto lavoro per nulla (o quasi…)? No, di certo… Siamo sicuramente pronti per capire cosa significhi realmente uno spazio curvo e, in particolare, uno spazio localmente curvo. Tuttavia, la Relatività Ristretta ci ammonisce di non essere troppo contenti. Abbiamo fatto solo un piccolo passo. Qualsiasi cosa faccia lo spazio non può non influire sul suo fratello gemello, il tempo. Ed è così che le equazioni di Einstein diventano molto meno semplici, ma permettono di costruire un regola che sembra più indistruttibile della stessa realtà delle cose. Lo spazio si lega al tempo e alle masse (ossia all’energia) e la faccenda diventa entusiasmante.

Tempo minimo o tempo massimo?

E’ stato bello e interessante lavorare in uno spazio sia piano che curvo, a due o a tre dimensioni. Tuttavia, non possiamo dimenticarci che qualsiasi cosa avvenga nello spazio non può non costringere a cambiare anche il tempo. Potremmo già concludere che, se curvo una cosa, devo curvare anche l’altra. Tuttavia, noi siamo interessati non a curvare separatamente le due “cose”, ma a curvare l’unione delle due, ossia lo spaziotempo.

In poche parole, dobbiamo descrivere il moto spaziotemporale. Ce l’ha, in  fondo, già insegnato benissimo Einstein, con l’aiuto del diagramma di Minkowski. In breve: ce l’ha dimostrato la Relatività Ristretta. Qualcuno troverà banale questo articolo (tutto è già stato detto negli approfondimenti, QUI e QUI), ma non credo faccia male riprendere certi concetti base che ci serviranno nel nuovo contesto.

In particolare cosa ha detto Einstein? Stiamo attenti a muoverci nello spazio e a misurare tranquillamente i tempi che impieghiamo per eseguire certi percorsi. Non tutti vedono la stessa cosa. Questo poteva andare bene per Galileo, ma non per noi! A seconda della velocità con cui ci muoviamo, il tempo è costretto a deformarsi rispetto a un certo sistema di riferimento.

Gli orologi di chi viaggia si vedono rallentare sempre più, a mano a mano che la velocità di chi li trasporta aumenta. Al limite, se si viaggiasse alla velocità della luce, gli orologi apparirebbero fermi. Ovviamente, non per chi viaggia, ma per chi guarda da un altro sistema.

Non vogliamo certo riscrivere la Relatività Ristretta e la trasformazione di Lorentz.  Ci basta, in fondo, una sola figura per riassumere la parte che più ci interessa e vedere come viene misurato il tempo, anzi... lo spaziotempo. Ma, prima, facciamo una piccola chiacchierata, tanto per richiamare alcuni concetti fondamentali. Un richiamo non fa mai male…

Consideriamo un sistema di riferimento considerato fermo, il cui tempo T viene misurato lungo la retta perpendicolare allo spazio monodimensionale (per adesso basta e avanza). Immaginiamo di non muoverci e di venire trascinati solo dal tempo (Fig. 7).

Il nostro orologio (che portiamo in tasca), ma anche i battiti del nostro cuore, scandiscono perfettamente il tempo che passa. Dopo 30 minuti (che possiamo considerare un “tempo unitario”) la nostra lancetta ha ruotato di 180 gradi verso il basso. Chiamiamo questo tempo T₁, considerando T =0 quello all’inizio della misura.

Approfittiamo di questo richiamo, ma lo faremo ancora, per ricordare che TUTTO il sistema di riferimento segue le stesse regole. In particolare, tutti i suoi orologi sono sincronizzati tra loro e indicano lo stesso tempo, come ad esempio l’orologio nero sulla destra. Esso si muove nel tempo, ossia segna lo stesso identico tempo, di quello posto a sinistra.

Fin qui tutto bene. Se il tempo fosse uguale per tutti i sistemi di riferimento (come veniva ipotizzato da Galileo e Newton), vedremmo, all’interno di un’astronave che viaggia a una certa velocità (ossia con una traiettoria indicata dalle linee rettilinee inclinate), un orologio girare esattamente come quelli del sistema di riferimento fermo. Che bello che sarebbe… Ci potremmo muovere nello spazio senza che il tempo ne risenta. Oltretutto, qualsiasi traiettoria sarebbe consentita, ossia qualsiasi velocità. Curvare lo spazio sarebbe più che sufficiente...

A questo punto subentra quello “scocciatore” di Einstein e inizia a dire che la massima velocità ammissibile è quella della luce, ossia del nostro piccolo e instancabile fotone (lui non può mai fermarsi).

Va bene, basta scegliere con cura le coordinate del tempo e dello spazio ed è facile descrivere, nel miglior modo possibile, la traiettoria percorsa dalla luce. Essa è diretta a 45° rispetto all’asse del tempo e dello spazio. Ragione per cui niente può viaggiare con un’inclinazione più bassa rispetto allo spazio. Tutto ciò che si muove nel tempo deve stare tra l’asse del tempo e la retta arancione. La linea viola non può esistere.

Va beh, pazienza… fosse tutto qua il problema. Purtroppo la relatività dice anche altro, ossia obbliga il tempo a scorrere in modo diverso a seconda della velocità a cui si viaggia, sempre che venga osservato da uno stesso sistema di riferimento ipotizzato fermo. Chi viaggia, ovviamente, non si accorge di niente: per lui il proprio orologio va sempre nello stesso modo.

Questo "proprio" orologio segna quello che chiamiamo tempo proprio, uguale per qualsiasi velocità. Una vera e propria distanza spaziotemporale tra due eventi, che non cambia variando il sistema di riferimento, proprio come fa la distanza tra due punti nello spazio galileiano.

Questa costanza, fa sì che l’unità di tempo cambi a seconda della velocità con cui ci si muove, qualora il tutto venga rappresentato nel sistema di riferimento fermo. In altre parole, quando venga usata la rappresentazione spaziotemporale di Minkowski, come riportato in Fig. 8.

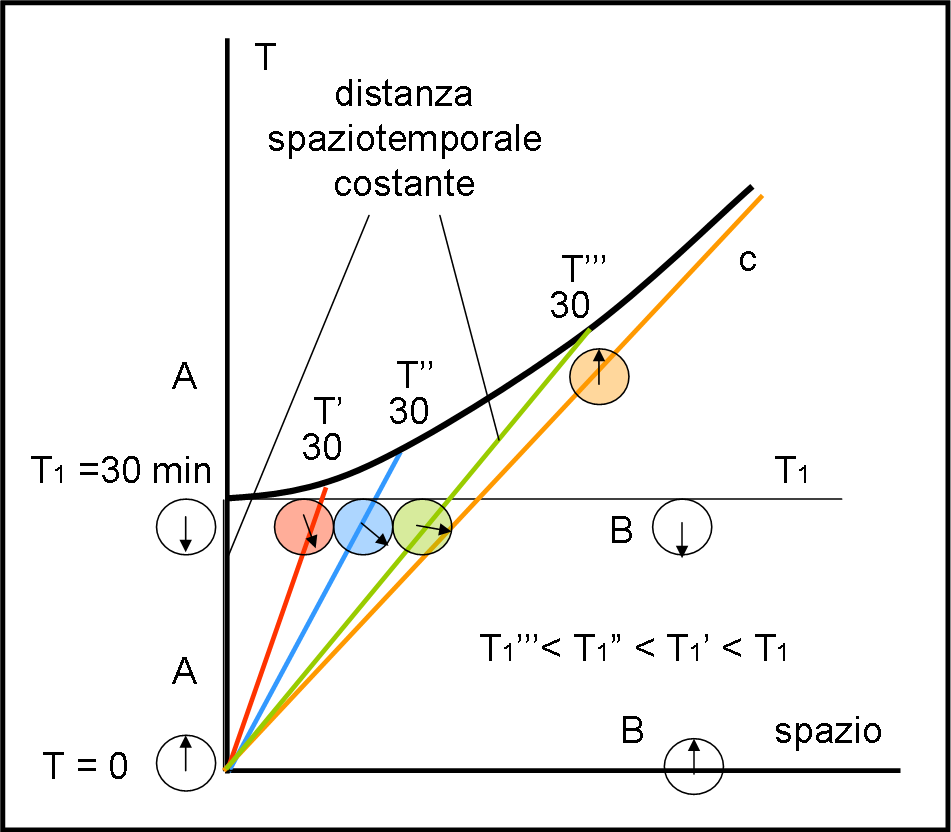
Più si va veloci e più l’unità di tempo si allunga. Addirittura, se si andasse alla velocità della luce, l’unità di tempo avrebbe una lunghezza infinita. Tutte queste parole possono essere sintetizzate da una bellissima curva (iperbole) tracciata in neretto nella figura. Ripetiamo: per chi viaggia il tempo corre sempre nello stesso modo. Per chi sta fermo questa costanza porta a una dilatazione dell’unità di tempo rispetto a quella del proprio orologio.

Ogni linea relativa a una certa velocità (l'asse del tempo) taglia l’iperbole in un punto. La distanza tra questo punto e l’origine degli assi (punto di partenza di ogni sistema) indica l’unità di tempo come viene vista da chi sta fermo. Questa unità non è certo costante se disegnata nello spazio di riferimento fermo, ma lo è, invece, nello spaziotempo e l’iperbole indica la linea di uguale distanza spaziotemporale rispetto alla comune origine.

No, non vi sbagliate di certo, stiamo proprio parlando del celebre invariante dello spaziotempo, una cosa analoga al raggio di una circonferenza in uno spazio piano, come già detto presentando il diagramma di Minkowski.

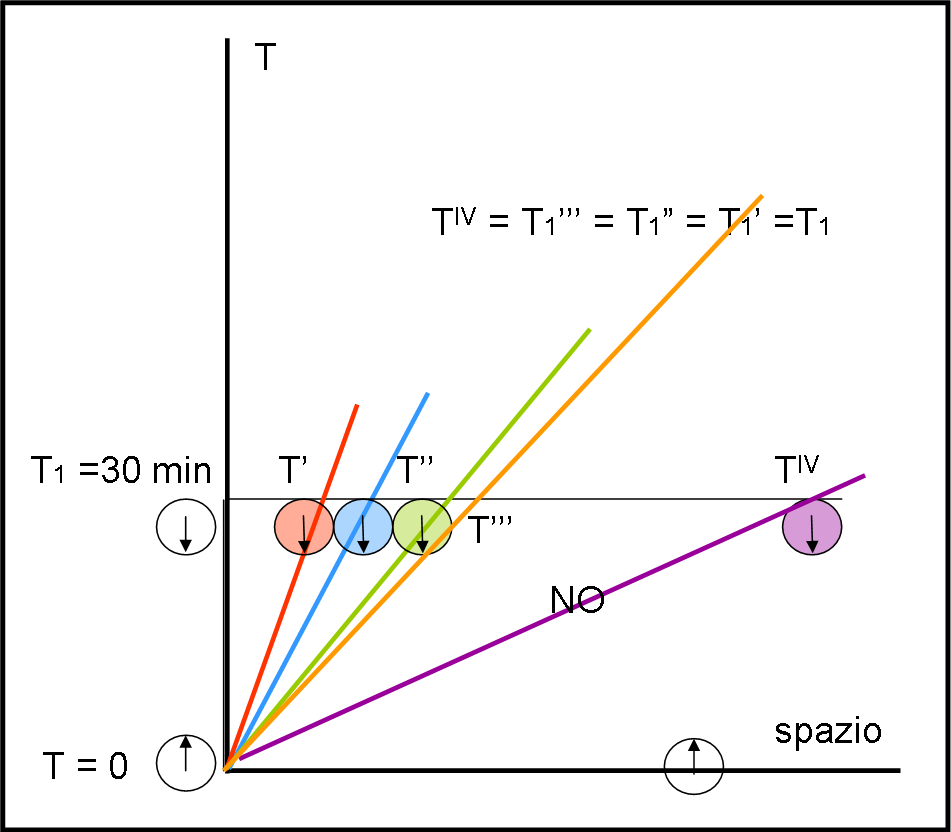
Cerchiamo di vedere le cose in modo più pratico. Ogni viaggiatore (rosso, blu e verde) ha un suo orologio dello stesso colore. Prima di muoversi segnano tutti zero, come quello di chi sta fermo.

Poi, via… verso nuove avventure, chi più veloce, chi meno! Cosa vede chi sta fermo confrontando i propri orologi perfettamente sincronizzati con quelli dei viaggiatori. Proprio quello che ci aspettavamo… essi girano più lentamente e rallentano sempre di più a mano a mano che la velocità aumenta. Come possiamo accorgerci di ciò, nella figura?

Beh, basta tracciare una linea orizzontale, relativa, ad esempio proprio a 30 minuti di tempo T. Se ci fosse Galileo direbbe che in quel momento tutti gli orologi colorati segnerebbero lo stesso tempo. Adesso, non più. La linea orizzontale, che indica un certo tempo T1 nel sistema fermo, incontra le linee colorate in punti (T1', T1" e T1"'), la cui distanza dall’origine è ben più corta dell’unità relativa alla singola linea, l’unità che scandisce il tempo proprio dell’orologio di chi si muove.

Apparentemente sembrano segmenti più lunghi, ma in realtà sono più corti se facciamo attenzione all’unità di misura di ognuno di loro. D’altra parte il tempo proprio è proprio scandito dalle diverse unità di tempo ed è lui stesso l’invariante relativistico, come si vede bene controllando le intersezioni con l’iperbole in neretto.

Noi, che stiamo fermi, siamo, però, muniti di orologi sincronizzati in qualsiasi punto dello spazio e possiamo fare il confronto tra orologi in moto e orologi del sistema fermo. Dirò adesso una cosa banale, ma che spesso mette in confusione… Non abbiamo bisogno che A abbia un “telescopio” per vedere gli orologi vagabondi, aspettando la loro luce. Se fosse così, introdurremmo un tempo supplementare che adesso non ci serve assolutamente. Basta, invece, avere una rete di orologi che si trovino al punto giusto, al momento giusto.

Ribadiamo: non c’è assolutamente bisogno di fare un confronto con l’orologio di A, che viaggia lungo l’asse del tempo in modo verticale, a una certa distanza spaziale dal punto d’incontro degli orologi colorati con la linea orizzontale, e che indica il tempo di chi sta fermo. Il confronto si può fare con qualsiasi orologio che appartenga al sistema e che, quindi, giri nello stesso identico modo. La sincronizzazione, all’interno di uno stesso sistema, non viene mai scalfita. Vi è sempre un orologio come quello di B, pronto a fare il confronto. In parole povere, l’astronave attraversala la linea orizzontale in un punto spaziale in cui è sempre presente un orologio che segni T.

Cosa vediamo, attraverso questa rete di orologi? Ci accorgiamo che la lancetta dell’orologio rosso è leggermente più indietro rispetto alla nostra, quella dell’orologio azzurro ancora di più e stessa cosa per quello verde (si è spostato di poco più della metà di quanto non si sia spostato il nostro). Per noi sono passati 30 minuti, ma l’orologio verde segna poco più di 15 minuti. E anche il  cuore dell'astronauta, la sua barba e ogni funzione vitale, è rallentata rispetto alla nostra. Il suo tempo proprio è uguale al nostro (una costante spaziotemporale), ma non ci appare così se viaggia velocissimo rispetto al sistema fermo.

Se guardassimo il fotone vedremmo un orologio (piccolo, piccolo…) che segna sempre e comunque le ore ZERO.

Di quanto rallentano gli orologi colorati? Beh… semplice a calcolarsi! basta fare il confronto tra la lunghezza di traiettoria compiuta e quella necessaria per arrivare all’iperbole, dove scatteranno i 30 minuti per ciascuno di loro. Il fotone raggiungerà l’iperbole solo all’infinito e quindi il suo tempo, per noi, appare sempre lo stesso.

Tutta questa complicazione dello spaziotempo è solo apparente? Assolutamente no, fino a che il viaggiatore si muove. Il suo orologio gira effettivamente più piano rispetto a noi che lo guardiamo. Il caso del muone ne è una prova inconfutabile (QUI). Tuttavia, è anche vero che se considerassimo fermo il sistema verde, ossia che si muove con l’astronave verde, e riferissimo tutto a lui, sarebbe il nostro orologio a subire un rallentamento perfettamente simmetrico. Questa è, in fondo, la base della Relatività Ristretta!

Prima di andare avanti, ribadiamo un concetto semplicissimo che, a volte, può creare confusione. Quando si dice che un orologio rallenta vuol dire che il tempo che misura è più piccolo. In altre parole, l’orologio dell’astronave più veloce è quello che misura il tempo minore.

A questo punto mi potreste dire: “Va bene, un ripasso della Relatività Ristretta fa sempre bene… ma noi vogliamo curvare lo spaziotempo e vogliamo introdurre la relatività generale…”. Calma e sangue freddo. Siamo entrati nello spaziotempo e vogliamo proprio definire le curve in questo nuovo ambiente. Dobbiamo, perciò, definire, prima, cosa si intende per traiettoria rettilinea tra due eventi (non possiamo più parlare di punti, dato che alla posizione abbiamo associato il tempo).

Altro che le già le difficili tre dimensioni del nostro spazio...

Vedremo che la risposta è esattamente il contrario di quanto si asserisce restando nello spazio. Per arrivarci, torniamo al paradosso dei gemelli che è solo un esempio di ciò che capita quando si è liberi di viaggiare nello spaziotempo. Anzi, prepariamoci ad una gara sportiva del futuro…

Riprendiamo la figura precedente e la chiamiamo Fig. 9, con lo stesso sistema di riferimento fermo.

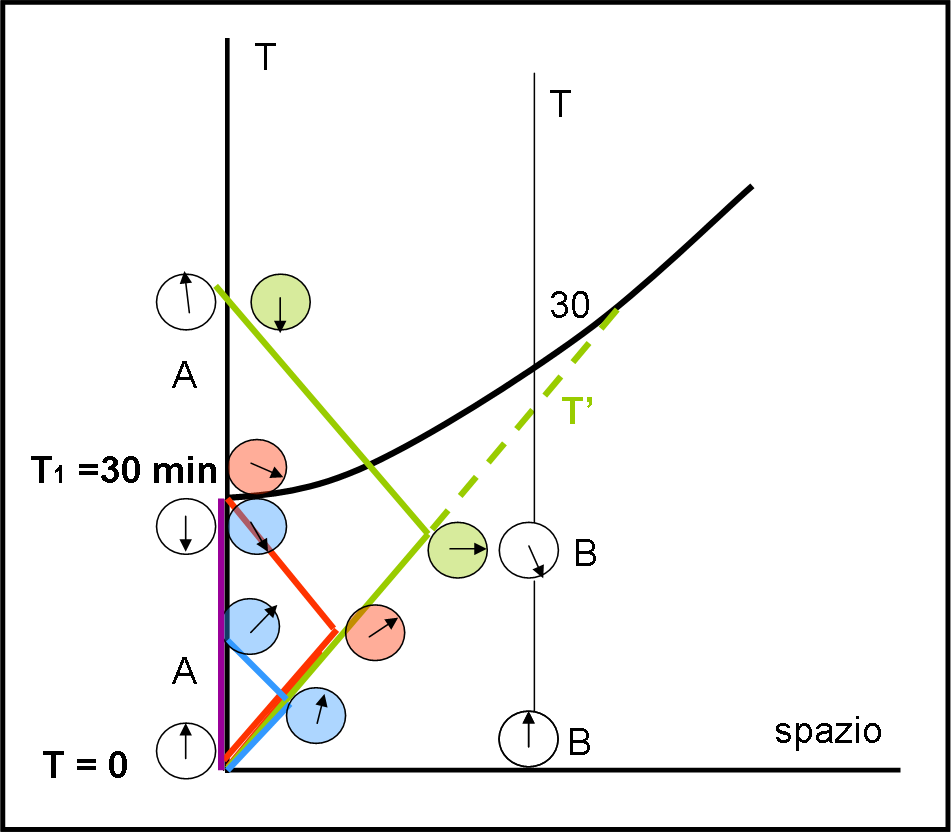
A sia il giudice “assoluto” della gara, che non si muove spazialmente dalla sua posizione di controllo. Intorno a lui ha tanti concorrenti pronti a eseguire l’esercizio che sta per proporre. Ferma, sulla pista dell’astroporto, vi è un’astronave nuova di zecca, che può raggiungere qualsiasi velocità (inferiore a quella della luce, ovviamente). Il compito da svolgere durante la gara è il seguente:

A un dato segnale viene dato il via al concorrente e dopo 30 minuti, misurati con l’orologio di A, sarà dato un secondo segnale. Vincerà la prova chi tornerà al punto di partenza, ossia in A, in tempo per ascoltare il secondo segnale, impiegando, però, secondo il suo orologio, il tempo più lungo possibile. L’ideale sarebbe, perciò, impiegare esattamente 30 minuti e riuscire a sentire il secondo segnale. Questa misura verrà effettuata dal giudice A, sulla base dell’orologio del viaggiatore.

Al limite, vincerà l’astronauta che più si avvicinerà ai 30 minuti. Attenzione: l’astronave impiega un tempo trascurabile per arrivare a una velocità di crociera e lo stesso capita per ogni cambiamento di percorso. Insomma, le accelerazioni e decelerazioni possono essere trascurate nel conteggio del tempo. E’ o non è un’astronave fantastica?!

Lanciato il segnale, parte il primo astronauta verde. Ha al suo servizio un mezzo velocissimo ed è convinto di fare ciò che vuole nello spazio e ritornare sicuramente in tempo per ascoltare il segnale. Deve solo fare attenzione a non tornare troppo tardi. Per essere sicuro decide di trascorrere nello spazio solo 29 minuti per non correre rischi. Il verde parte a una velocità fantastica e si diverte a vedere tutto ciò che lo circonda e non si accorge del sorriso ironico dei giudici “assistenti”, disposti lungo il percorso e che possono direttamente controllare il tempo che sta passando nell’abitacolo.

Il concorrente controlla la situazione, dopo essersi divertito per bene, e valuta che è l’ora di tornare indietro. Frenata quasi repentina e apre la cabina da cui scende felice con il suo orologio in mano. Lui stesso grida 29 minuti e 59 secondi! E attende il suono che indichi la conclusione della gara.

Intorno a lui molti stanno ridendo ed esclamano: “Era ora che arrivassi! E' una vita che è suonata la conclusione”. “Ma come”, dice lui, e mostra al giudice il suo orologio. Il giudice non dice niente e mostra il suo orologio, quello che fa fede per il secondo segnale. Mamma mia… è passato un tempo lunghissimo (non fatemi fare dei calcoli, quello che importa è il concetto). Grida: “Accidenti agli orologi e a chi li ha inventati” e va via con la coda tra le gambe.

Il secondo concorrente (rosso) ha avuto tempo di pensare a lungo, in attesa dell’avversario, e teme che non sia stato l’orologio a non funzionare: per andare sul sicuro e non fare la figura del compagno precedente, viaggia ad alta velocità per molto meno. Poi torna indietro giusto in tempo per sentire il secondo segnale. Il suo orologio purtroppo, segna un tempo decisamente più piccolo dei 30 minuti, ma è convinto che nessuno potrà impiegare più tempo per ascoltare il segnale conclusivo.

Il terzo concorrente (blu), però, malgrado l’estrema prudenza, fa meglio di lui, anche se è costretto a stare parecchio tempo in attesa, vicino al giudice, prima di sentire il segnale e mostrare il proprio orologio. Accidenti, non l’avrebbe mai detto, il suo tempo è decisamente più lungo e si avvicina molto ai 30 minuti.

Il quarto concorrente (viola) ha veramente capito tutto. Sale sull’astronave, ma non accende nemmeno il motore. Aspetta tranquillamente che si senta il segnale e mostra contento il suo orologio: esso segna esattamente 30 minuti. In parole molto banali: il concorrente viola non si è mosso, rispetto al sistema di riferimento dei giudici, e ha impiegato il tempo maggiore.

Sì, lo ammetto, siamo stati estremamente didattici e i più bravi -forse- si saranno annoiati un po’. Tuttavia, per i meno preparati è stato un ottimo esercizio. In entrambi i casi, però siamo arrivati a due conclusioni fondamentali per sapere valutare la curvatura dello spaziotempo.

Analizziamo con calma ciò che è successo, tenendo per noi il fatto indiscutibile che almeno tre dei quattro concorrenti non conoscevano affatto la Relatività Ristretta!

Il concorrente verde si è fidato ciecamente del suo orologio e dopo che erano trascorsi circa 15 minuti ha deciso di tornare indietro. E’ arrivato esattamente in 30 minuti, ma non ha tenuto in conto che il segnale sarebbe stato dato dopo 30 minuti dell’orologio del giudice. Sì, lui ha ottenuto un tempo molto lungo e praticamente uguale a quello massimo, ma non ha potuto sentire il secondo segnale!

Siamo esattamente nel caso del paradosso dei gemelli: il concorrente verde torna a casa veramente più giovane del giudice, ma non ha superato la prova.

Il concorrente rosso, non ha ancora capito bene la faccenda e preferisce tornare a casa molto prima dei 30 minuti del suo orologio e riesce a sentire il secondo segnale. Tuttavia, il suo orologio segna molto meno dei 30 minuti, risultato che gli avrebbe dato la vittoria sicura.

Anche se con meno evidenza si ripete il paradosso dei gemelli: il secondo segnale viene sentito dall’astronauta solo una ventina di minuti dopo la sua partenza.

Il concorrente blu è molto imbarazzato e -pensiamo- abbia voluto, comunque, fare un giro in astronave, senza nemmeno pensare alla gara. Eppure, con sua grande sorpresa impiega nettamente più tempo per sentire il secondo segnale. Ci si avvicina moltissimo.

Il quarto, probabilmente, conosce la Relatività Ristretta o ha fatto tesoro dei risultati dei suoi compagni. Non muovendosi è sicuro di sentire il secondo segnale dopo 30 dei suoi minuti, dato che sono esattamente uguali a quelli del giudice. Avrà sempre tempo per provare l’astronave...

Ammettiamolo… mi sono divertito un po’ a creare diverse situazioni che, comunque, portano sempre a una sola conclusione, che già conoscevamo fin da quando abbiamo discusso il diagramma di Minkowski (QUI). La linea verticale, continua, del tempo è quella in cui si ottiene il massimo tempo di percorrenza, che, in altre parole ci dice che nello spaziotempo un cateto è sempre maggiore dell’ipotenusa. Mentre nello spazio il quadrato di una distanza è dato dalla somma dei quadrati delle due coordinate (x e y), nello spaziotempo il quadrato di un cateto (T)  è uguale alla somma dei quadrati dell’ipotenusa (T’) e dell’altro cateto x. Ossia:

d² = x² + y²

T² = T’² + x²

Una soluzione che già conoscevamo, ma che adesso acquista una grande importanza, se enunciata in modo leggermente diverso. Consideriamo un'astronave che viaggi da A a B (due punti fissi nello spazio). Per raggiungere i due punti potrebbe usare velocità diverse. Potrebbe tentarle tutte (andare prima velocissimo e poi a passo di lumaca o viceversa), ma impiegherebbe sempre più tempo andando a velocità uniforme da A a B. Per capire perfettamente questo concetto, basterebbe cambiare sistema di riferimento e considerare ferma l’astronave (il giudice si muoverebbe con velocità uguale e opposta) e ricadremmo nella “gara” precedente.

Si può perciò dire che nello spaziotempo la linea retta è quella descrivibile con una velocità uniforme e direzione costante, che comporta anche il maggior tempo misurato con l’orologio di chi la percorre

Questa definizione prende il posto di quella analoga utilizzata nello spazio (retta euclidea o retta intrinseca per spazi non euclidei). Quest’ultima, però, definiva anche la curva di minima distanza e di conseguenza la curva percorribile nel minor tempo possibile (chiedetelo ai piloti degli aerei…).

Riassumendo: la curva di minima distanza nello spazio, che è quella che comporta il minimo tempo per essere percorsa, corrisponde nello spaziotempo alla curva percorribile nel tempo più lungo. Esattamente il contrario!

Il moto lungo una linea retta nello spaziotempo è il moto che fa passare da un evento a un altro nel massimo tempo possibile. In altre parole, il moto rettilineo nello spaziotempo è quel moto che fa passare un orologio da un punto, in un certo tempo, a un altro punto, in un altro tempo, in modo tale che la differenza di tempo misurata sull’orologio di bordo sia la massima possibile.

Questa sarà la nostra “retta” di riferimento spaziotemporale, in base alla quale misureremo eventuali curvature.  Attenzione che fino ad adesso abbiamo ragionato SOLO in  termini di relatività ristretta proprio per definire cosa sia la linea intrinsecamente retta. Quando capiterà qualcosa che deformerà lo spaziotempo, ce ne potremo accorgere abbastanza facilmente (si fa per dire).

Anticipiamo un concetto che sarà alla base di molte conseguenze. Nella Relatività Ristretta, se io sto fermo vedo tizio che corre quasi come un fotone. Per il tizio che corre, però, sono io che schizzo a velocità pazzesca. Tutto è perfettamente simmetrico.

Se, invece, inserisco una “stufa” molto strana in un punto dello spazio, la faccenda perde di simmetria. Solo un sistema subisce gli effetti della stufa (ossia della massa), l’altro guarda  soltanto. Il sistema lontano vede la stufa e può calcolarne gli effetti. Chi è vicino alla stufa può ribaltare la situazione? Assolutamente no: la stufa non può trasferirsi da un sistema all’altro. Chi è vicino alla stufa non può dire che rispetto a lui, la stufa si sposta nell’altro sistema di riferimento. La simmetria della Relatività Ristretta non c'è più.

Abbiamo detto cose già conosciute ai più, ma sono cose sempre abbastanza ostiche concettualmente, e non è male inquadrarle nel contesto che ci interessa...

Basta un imbianchino per il Principio di Equivalenza.

Galileo ha avuto i suoi gravi, Newton ha avuto la sua mela ed Einstein ha avuto il suo … imbianchino. Ebbene sì, sembra che l’idea più straordinaria che abbia avuto Einstein (secondo le sue stesse parole) gli sia venuta parlando con un imbianchino che era caduto da un’impalcatura di fronte al suo palazzo. Dopo di allora, forze apparenti, inerzia, accelerazione, gravità hanno iniziato a cambiare completamente la loro descrizione (in pratica sono scomparse) e, allo stesso modo, le conclusioni di Galilelo e  Newton sull’uguaglianza “fortunata” di massa gravitazionale e massa inerziale, è diventata l’ovvia conseguenza della gravità.

E' giunta l'ora di far vedere come il significato di inerzia e di forze apparenti diventi del tutto “trascurabile”  o addirittura “privo di senso”, quando si arrivi all’equivalenza tra sistema accelerato e campo gravitazionale.

Le parole dette dal povero imbianchino, uscito solo un po’ malconcio, furono piuttosto banali, ma non per Einstein: “Mentre cadevo mi sono accorto di essere senza peso… una strana sensazione!”. Nella mente del grande genio scoccò la scintilla che stravolse tutte le leggi della dinamica newtoniana, ribaltandone il senso. Vedete come riesce a ragionare Einstein, un fanciullo con la mente sgombra da ogni pregiudizio? Una banalità diventa una legge fondamentale. Forse ancora più semplicemente della famosa mela...

Ricordiamo che Galileo (grazie agli esperimenti con il piano inclinato) e Newton avevano già concluso che tutti i corpi cadono con la stessa accelerazione, il che comporta che la massa gravitazionale è uguale a quella inerziale e, ancora, che un corpo in caduta libera è soggetto a una forza apparente uguale e contraria a quella di gravità, tale da farlo sentire immobile nel suo sistema di riferimento (ne avevamo parlato anche QUI). Parliamoci chiaro: il peso (che è una forza), si sente solo quando agiamo sul terreno, o su superfici analoghe, che ci vietano la caduta verso il centro della Terra. Il peso, o -meglio- le conseguenze del peso, si sentono solo come risposta (terzo principio) della Terra verso di noi!

Einstein accetta tutto ciò, ma ribalta la situazione, assumendo che le “strane” evidenze osservative dei suoi illustri predecessori, non erano frutto di strane coincidenze, ma erano descritte completamente dalla natura stessa della gravità. Non è un caso che massa gravitazionale e massa inerziale siano uguali, come dicono le osservazioni, ma una conseguenza della nuova visione geometrica della gravità. Tutto è perciò da riscrivere, comprese le forze stesse agenti su una massa immersa in un campo gravitazionale o, comunque, accelerato

Einstein decide di rappresentare la gravità attraverso la geometria dello spazio, proprio in un momento in cui la Scienza ufficiale si sta dirigendo sempre di più verso il mondo sconosciuto e assurdo della meccanica quantistica . Una specie di “conservatore” a oltranza (anche se una delle prove osservative più importanti della MQ proviene proprio dal SUO effetto fotoelettrico ). Una rivoluzione “poco moderna”, che porta però a una teoria praticamente perfetta, che la MQ non riesce ancora a far sua.

Entriamo, allora, nella trattazione, addirittura infantile, del principio di equivalenza. In fondo, basta solo fare un po’ di chiarezza sulle forze vere e apparenti che tanto sono servite al nostro Alberto per impostare la sua rivoluzione, quasi inconcepibile per le altre menti, come ebbe a dire lo stesso Feynman. Pensiamoci e non smettiamo mai di farlo: il principio di equivalenza appare proprio come un uovo di Colombo, eppure solo una mente infantile e superiore poteva vederne la portata immensa e, soprattutto, non aver timore di esporla.

Consideriamo due sistemi di riferimento e una scatola contenente due semplici palline di massa  (ed energia) diverse. Cerchiamo di descrivere cosa succede se la scatola viene inserita in un ambiente PRIVO di gravità e in un campo gravitazionale.

Consideriamo la Fig. 10.

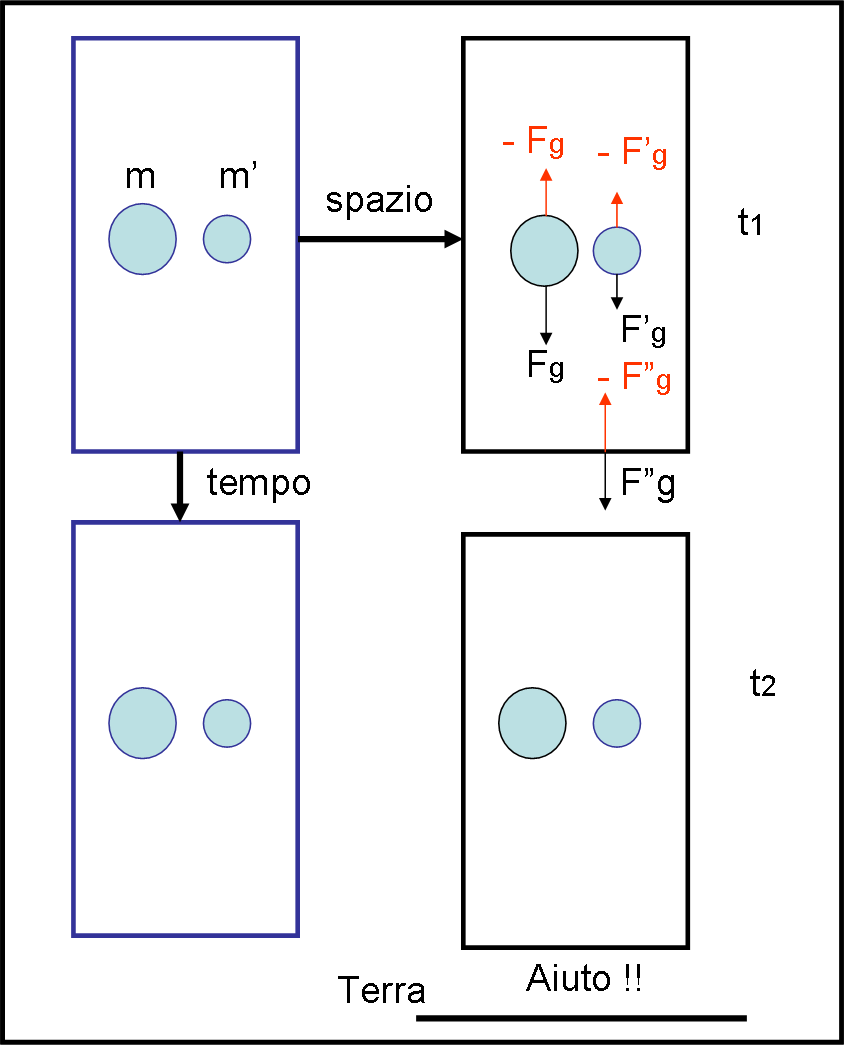
A sinistra abbiamo la nostra scatola talmente lontana da qualsiasi massa aliena che su di lei non agisce alcuna forza gravitazionale. Scatola e palline possono essere considerate ferme o, se preferiamo, in moto rettilineo uniforme, come dice il primo principio della dinamica. Le palline sono sospese nel vuoto, e tali rimangono dato che non vi è alcun movimento relativo uniforme tra scatola e palline (relatività ristretta).

L’osservatore esterno può vedere il tutto viaggiare a velocità costante o anche vedere il tutto immobile. Poco importa, dato che siamo di fronte a sistemi inerziali e il sistema della scatola può tranquillamente considerarsi fermo. Le palline non hanno peso… non solo, però, non sanno nemmeno cosa significhi la parola peso. Esse hanno solo massa, ossia energia (l’equivalenza tra massa ed energia l’abbiamo approfondita nelle lezioni di Dinamica Relativistica).

Al passare del tempo (verticale) niente cambia nel sistema sia se viene visto da fuori sia se viene osservato dal suo interno (in modo solidale con le palline e la scatola).

A destra, invece, spostiamo la scatola e la lasciamo in balia di un campo gravitazionale. Essa, insieme alle due palline, inizia a cadere verso il suolo sotto l’azione della forza di gravità. Il sistema non è più inerziale e tutto cambia se visto da fuori o dall’interno, seguendo, però, la regola fondamentale che il fenomeno meccanico (e anche fisico, dopo la RR) deve rimanere lo stesso.

Chi sta fuori non può che essere spaventato: la scatola  e la pallina stanno cadendo a grandissima velocità… anzi, una velocità che aumenta istante per istante (l’imbianchino è caduto dall’impalcatura…).Tuttavia, se riusciamo a intervistare le palline (o l’imbianchino oppure il nostro Ciccio nell’ascensore), esse ci dicono che non pensano proprio di cadere: la parola peso è per loro del tutto sconosciuta. Tutto avviene esattamente come nell’esperienza fatta precedentemente nel vuoto.

Il problema esiste solo per l’osservatore esterno che deve cercare di spiegare come tutto ciò possa succedere. E’ lui che introduce una forza peso ed è lui che è costretto a far sì che le due palline si sentano perfettamente a loro agio. Le palline, in realtà non sentono la forza peso e, quindi, ciò implica che se veramente esistesse loro dovrebbero essere trattenute da una forza uguale e opposta. Chi ne ha veramente bisogno? Loro o l’osservatore esterno per cercare di avvalorare le proprie convinzioni?

Mi permettete di dire una cosa, piuttosto imbarazzante? Se tutta la massa della Terra fosse concentrata in un punto (cosa che già Newton aveva ipotizzato), la forza peso (o gravità, come preferite) non avrebbe alcun senso per le due palline e, di conseguenza anche tutti gli sforzi atti a cercare di descrivere l’intera faccenda con gli occhi di un osservatore esterno. Le palline sarebbero in caduta libera fino all'incontro con un punto in cui è concentrata tutta la massa della Terra. Una rappresentazione assurda che, però, aiuterebbe a vedere il tutto come una pura rappresentazione geometrica (ricordiamo la "strana" piastra calda). In fondo, basterebbe cambiare la visione complessiva della situazione…ed è quello che Einstein inizia a capire guardando l’imbianchino e parlando con lui… "il giorno più bello della sua vita!".

Cerchiamo di seguire il ragionamento dell’osservatore esterno.

Egli vede che tutto sta cadendo verso la Terra (scatola e palline) con la stessa velocità. Per lui è in azione la forza F_g, la quale impone un’accelerazione costante a tutto ciò che cade. Ha accettato l’idea che massa inerziale e massa gravitazionale siano uguali e quindi può dire che la forza, uguale alla massa moltiplicata per l’accelerazione (F = ma), utilizzi un massa che è la stessa che entra nella “sua” forza peso. La massa di chi cade sparisce e questo comporta che la velocità di qualsiasi oggetto (sempre più alta) rimanga la stessa per qualsiasi massa.

Non può, perciò, stupirsi più di tanto se alle palline sembra che tutto sia immobile come nel vuoto cosmico. Può anche spiegare alle palline che il loro non-peso “apparente” è dovuto all’entrata in azione, nel loro sistema di riferimento, di forze uguali e contrarie a quella di gravità ( -F_g), tali da farli sentire in completo riposo.

Il fenomeno fisico, anche se con qualche difficoltà, non cambia assolutamente. Le palline possono anche dargli ragione, ma ciò che sentono è molto più semplice da spiegare. Su di loro non si esercita nessuna forza o accelerazione. Tuttavia, se veramente esiste una forza peso, allora loro sentono prepotentemente la forza apparente che l’annulla. Per loro la forza DEVE essere reale.

L’unica vera differenza è che l’osservatore esterno sa benissimo che al momento dell’impatto al suolo, le forze apparenti svaniranno, dato che il sistema in caduta libera non sarà più tale, e la forza gravitazionale darà luogo a una reazione uguale e contraria per il terzo principio della dinamica. Per lui la differenza tra sistema nel vuoto cosmico e sistema in preda al campo di gravità è decisamente grande. Non solo. Egli sa anche benissimo che questa reazione non dipende solo dall’accelerazione, ma anche dalla massa e il cratere formato dalle due sfere deve anche essere diverso (Fig. 11). Quello che conta non è più soltanto la velocità, ma anche la massa, come spiega bene l’energia cinetica (1/2 mv²).

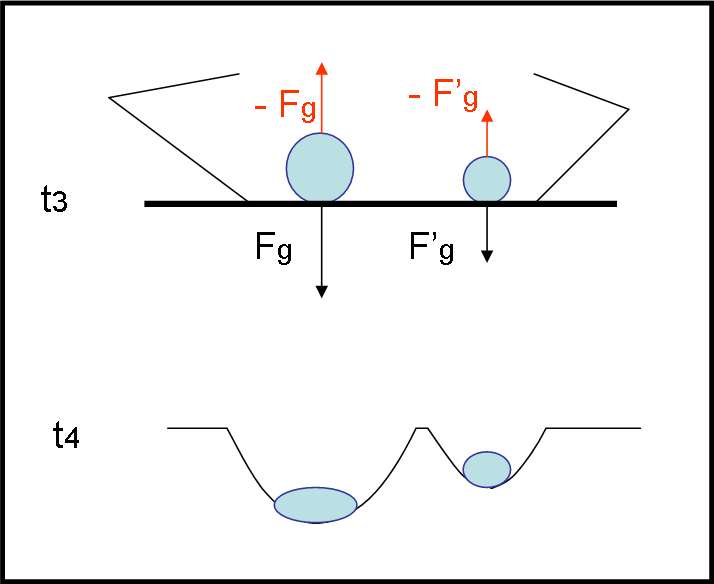
In poche parole, ben più generali, si può concludere che un corpo in caduta libera si comporta esattamente come un corpo che non è soggetto a nessuna forza o accelerazione. Se tutto il sistema segue la legge gravitazionale, nessuno può accorgersi della differenza delle due situazioni. L’idea di una situazione puramente geometrica comincia a farsi largo.

In pratica è stato detto che:

Un sistema di riferimento in caduta libera (ossia soggetto solo alla forza gravitazionale) e un riferimento inerziale sono del tutto equivalenti.

Possiamo anche lanciarci più in là e dire: “La geometria dell’ambiente è tale che conta poco la massa degli oggetti che stanno cadendo… loro seguono solo delle direzioni prestabilite. O -ancora più esplicitamente- poco importa quale sia la massa o l’energia coinvolta, dato che siamo di fronte a un problema puramente geometrico. Le masse non fanno altro che seguire le strade che la geometria ha preparato per loro. Avete presente uno scalo ferroviario con tanti scambi e tanti binari che vanno ognuno per i fatti suoi e a cui poco importa la massa del treno che sta arrivando? La differenza di massa e di energia si valuterà solo se avverrà uno scontro.”

Una visione completamente ribaltata rispetto a quella di Newton e Galileo. E tutto ciò grazie a un imbianchino caduto da un’impalcatura… Forza peso, forze apparenti, unicità dell’accelerazione stanno diventando ovvie conseguenze di una geometria particolare.

Tuttavia, possiamo tranquillamente procedere nel nostro tentativo di equivalenza ed estenderlo a un riferimento che non sia accelerato dalla gravità. Se esiste l’equivalenza di prima, dobbiamo continuare a confermarla.

Prendiamo la nostra scatola nel vuoto, fuori da ogni campo gravitazionale. Ci accorgiamo però che abbiamo a disposizione un motore, ossia un qualcosa capace di variare la velocità del sistema. Ovviamente, non può agire su tutto il sistema, ma solo sulla scatola. Le palline non possono risentire direttamente dell’accelerazione impartita alla scatola.

Tuttavia, succede qualcosa di strano… per chi sta all’esterno del sistema accelerato (Fig. 12, a sinistra).

Le palline restano ferme (nessuno le ha accelerate o -se preferiamo- sono “inerti”) mentre si muove la scatola. Attenzione per muoversi deve accelerare, ossia cambiare la velocità precedente, sia che fosse zero sia che fosse un valore costante, lo stesso delle palline.

In breve, la parete di fondo non può che andare a scontrarsi con le palline. La palline subiscono un forza da parte della parete e per il terzo principio della dinamica esse devono rispondere esercitando sulla parete una forza uguale e contraria. Questa non è una forza apparente, ma una forza legata alla reazione. Una forza che vale proprio –ma e –m’a, se a è l’accelerazione della scatola.

Notiamo che a deve essere la stessa per le due palline, dato che è quella, unica, della scatola. Non sono invece uguali le forze subite dalle due palline, così come quando cadevano sulla Terra (o era la Terra che le veniva incontro come, adesso, il fondo della scatola?)

Portiamoci all’interno della scatola. Le palline vedono solo le pareti, che, ovviamente considerano ferme. Tuttavia, quella di fondo le si avvicina velocemente. Non possono che concludere che sono loro due che si stanno muovendo con una certa velocità diversa da prima, ossia che sono soggette a un’accelerazione che la porta verso il fondo della scatola. Stranamente, malgrado esse abbiano massa diversa, l’accelerazione è la stessa. Qualcosa di molto simile a quello che gli hanno raccontato mentre cadevano verso la Terra e si sentivano senza peso. Allora non si aspettavano l’impatto, ma adesso lo vedono arrivare con grande paura.

Adesso, finalmente, capiscono cosa sia la forza peso e che rischi comporti. Purtroppo, anche loro, subiscono lo scontro legato al terzo principio: la parete risponderà alla loro forza,  con una reazione uguale e contraria che le farà fermare. Il fenomeno rimane identico nei due sistemi.

Dov’è la forza apparente? Beh, è sicuramente quella che sembra portarle verso il fondo, ma è così “fittizia” che è capace di creare una forza uguale e contraria nell’urto. In analogia a quanto è successo cadendo verso terra, sotto l’effetto della gravità, si può concludere che la forza fittizia è proprio qualcosa di identico alla forza di gravità! Questa volta, però, niente la viene ad annullare.

Possiamo dare il nome che vogliamo alle forze che abbiamo incontrato, ma resta il fatto che le palline si muovono geometricamente verso il basso per effetto di un’accelerazione, diretta o indiretta che sia. Se vediamo il sistema da fuori, le palline restano ferme e le viene incontro la parete. Se siamo all’interno del sistema sono le palline che si muovono fino a scontrarsi con la parete.

Bene, passiamo, nuovamente, a un sistema dominato dalla forza di gravità. Immaginiamo di prendere il nostro sistema inerziale e di poggiarlo a terra (Fig 12, a destra). La scatola non può muoversi dato che la parete di fondo imprime una forza contro il suolo e il suolo prontamente risponde con una forza uguale e contraria (terzo principio della dinamica). Attenzione: questo vuol dire che la scatola fa parte del sistema Terra. Le palline però, non sono poggiate a terra e quindi risentono della forza di gravità e cadono verso il suolo con la stessa accelerazione uguale a g.

La conclusione è che chi sta fuori vede le palline cadere verso il suolo, dominate da un’accelerazione ben definita g. La stessa cosa capita, però, anche alle palline che stanno dentro.

Finalmente tutto sembra uguale sia per un osservatore esterno sia per uno interno. Il fenomeno fisico è chiaramente lo stesso, senza dovere introdurre forze apparenti. La cosa è del tutto ovvia, dato che il sistema della scatola non è più un sistema diverso da quello terrestre. Si può togliere tranquillamente la scatola che fa ormai parte della Terra, essendo immobile su di lei. Le due palline cadono al suolo senza nessun aiuto esterno che cerchi di fermarle.

Possiamo veramente concludere che niente è assolutamente cambiato rispetto all’esperimento precedente: un sistema accelerato è del tutto equivalente a un sistema su cui agisce solo la forza di gravità.  Possiamo cambiare le parole per spiegarlo, ma è indubbio che una nuova definizione della gravità potrebbe sistemare tutto sotto un unico ombrello, puramente geometrico, annullando forze reali e fittizie che si scambiano il ruolo continuamente.

Nasce il principio di equivalenza einsteniano:

Gli effetti dovuti all’inerzia, all’interno di una scatola uniformemente accelerata, in uno spazio non affetto da forze gravitazionali, sono equivalenti a quelli che si verificano in campo gravitazionale omogeneo. In altre parole: un’accelerazione uniforme crea un  campo gravitazionale uniforme.

Notiamo bene la parola omogeneo… proprio la parola che ci farà curvare il mondo. La scatola non può essere considerata omogenea, dato che l’accelerazione di gravità g è costante solo LOCALMENTE. La gravità non è ancora del tutto pronta a essere sostituita da un sistema di riferimento accelerato.

Ribadiamo meglio questo concetto: anche se la scatola fosse grande, l’accelerazione che gli viene impressa è uguale per tutte le parti della scatola e, di conseguenza, anche l’accelerazione più o meno fittizia che sentono le palline. Se invece scatola e palline vengono inserite in un campo gravitazionale, le accelerazioni (di gravità) cambiamo da zona a zona della scatola. Per avere una perfetta equivalenza bisognerebbe considerare una scatola infinitesima che abbia una distanza unica dalla Terra e due palline per le quali siano trascurabili perfino le forze mareali.

Il principio di equivalenza si fa più sottile e le traiettorie di caduta geometriche sono costrette a deformarsi.

Il tempo non è da meno

Abbiamo fatto un passo fondamentale verso la relatività generale. Il principio di equivalenza che pone sullo stesso piano un sistema accelerato e un sistema sotto l’effetto della gravità comporta conseguenze quasi inaspettate anche sul tempo. La famosa "piastra" torna in campo…

Andiamo a comprare (o ci fabbrichiamo) due orologi veramente precisi e portiamoci all’interno di un’astronave. Uno lo inseriamo nella parte “alta” (A) e uno nella parte “bassa” (B) di Fig. 13.

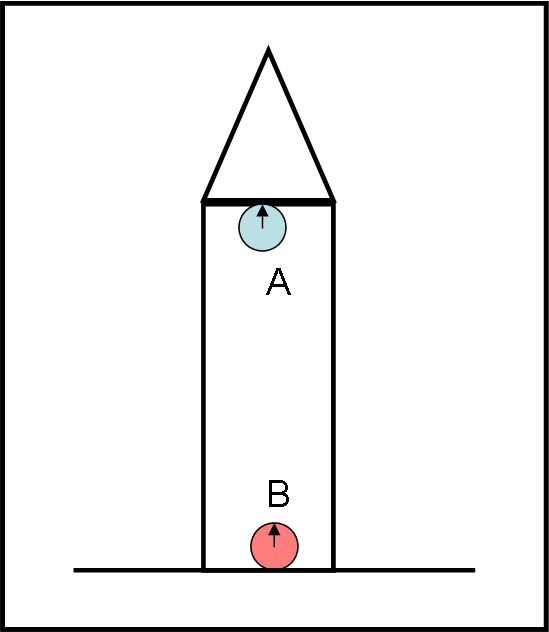
Prima di partire li controlliamo attentamente. Sembra che siano veramente perfetti. Per sicurezza estrema, facciamo un controllo ulteriore: l’orologio A spara ogni secondo un raggio di luce. L’orologio B lo riceve e può confermare che i segnali luminosi sono intervallati esattamente di un secondo. Un osservatore si mette vicino all’orologio A e uno vicino all’orologio B. Magnifico, si può partire accelerando in modo costante.

Continuiamo l’operazione di prima (non si sa mai e poi ce l’ha consigliato un certo Einstein), ossia a ogni secondo che passa, l’orologio A invia un segnale luminoso verso la parte posteriore.

La situazione, all’istante dell’invio della prima luce, è quella rappresentata in Fig. 14a (tempo zero), mentre quella dell’arrivo del segnale in B è la Fig. 14b. Per semplificare la faccenda immaginiamo che per arrivare in B la luce abbia impiegato proprio un secondo. Il che vuol dire che A può inviare il secondo segnale verso B, che lo riceve in Fig. 14c. L’osservatore A ha mantenuto perfettamente  il secondo di intervallo. Per notare meglio le differenze, la lancetta dei nostri orologi si sposta di 90° ogni secondo (sono o non sono ultra precisi?).

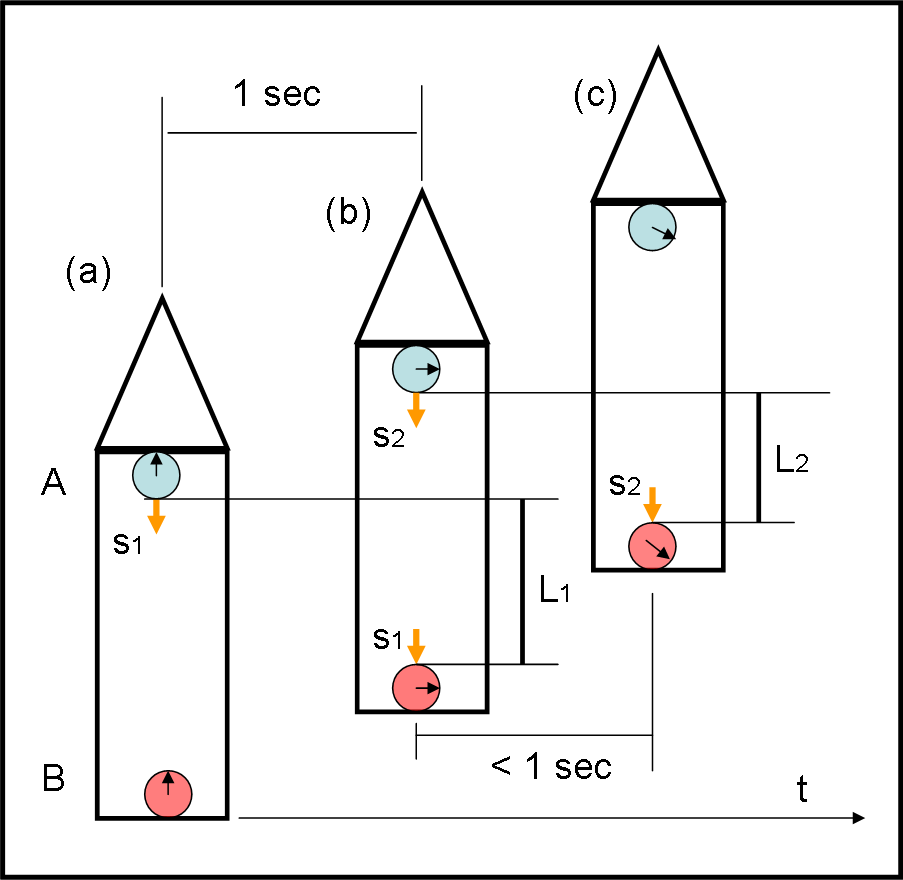
Cosa nota l’osservatore in B? Ammettiamo, come già detto, che l’orologio B riceva il primo segnale proprio nell’istante t = 1 secondo. Non gli resta adesso che attendere che arrivi il secondo segnale. E’ pronto a giurare che la luce arriverà dopo un altro secondo.

E, invece no. Accidenti, l’osservatore in B deve ammettere che c’è qualcosa che non va! Per lui non è assolutamente passato un secondo, ma decisamente meno! Sa benissimo che il suo orologio non sbaglia un colpo. E’ costretto a concludere che l’orologio di A va più veloce del suo! Ha infatti inviato i due segnali, intervallati tra di loro di meno di un secondo. E il risultato continua a verificarsi al passare del tempo.

La faccenda sembra strana, ma non poi tanto. Immaginiamo che anche l’orologio B invii un segnale luminoso ogni secondo. Questa volta anche l’osservatore posto vicino ad A rimane alquanto sorpreso. Il secondo segnale gli arriva dopo un intervallo maggiore di un secondo. Non può che concludere che l’orologio B va più lento del suo, come vediamo nella Fig. 15a,b,c.

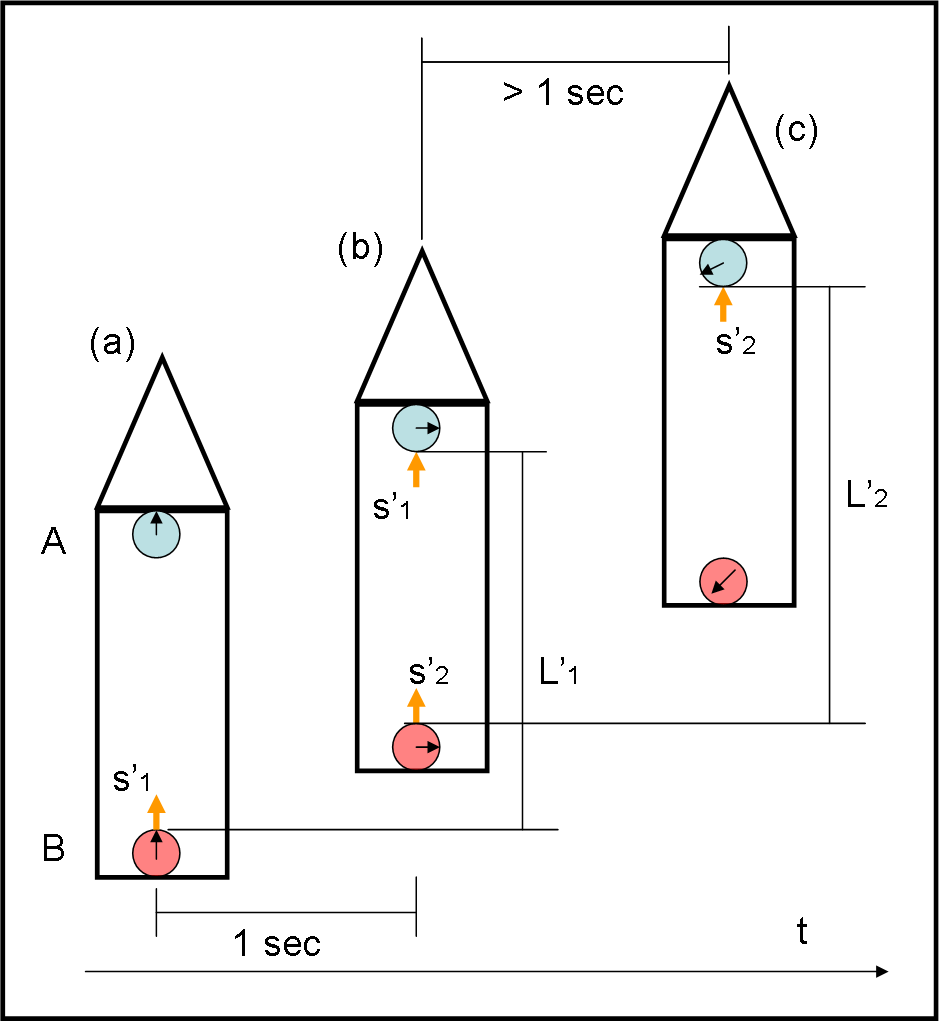
In poche parole arrivano entrambi allo stesso risultato: per l’osservatore in B è l’orologio A che va più velocemente, per l’osservatore in A è l’orologio in B che va più lentamente. Perfetto nella sua stranezza, dato che all’inizio sembravano andare così bene entrambi. Non sono più in accordo tra loro e quello più “alto” segna un tempo maggiore (l’orologio va più in fretta) o -se preferiamo- è quello in B che segna un tempo minore (l’orologio va più lentamente). In fondo, concordano tra di loro: uno dei due è sicuramente andato in “tilt”.

Avessero tenuto conto dell’accelerazione, non si sarebbero certo stupiti e non avrebbero dato la colpa agli orologi. Il segnale di A impiega sempre meno tempo per arrivare in B in quanto B va sempre più velocemente incontro alla luce. Il segnale di B impiega, invece, più tempo ad arrivare in A, dato che A si allontana sempre più velocemente. La variazione di velocità è costante, il che vuol dire che lo spazio percorso cresce col tempo (legge del moto uniformemente accelerato).

Notiamo, infatti, che non sarebbe successo niente se l’astronave si fosse mossa a velocità costante il segnale sarebbe partito e arrivato sempre a intervalli di un secondo (Fig 16a,b,c)

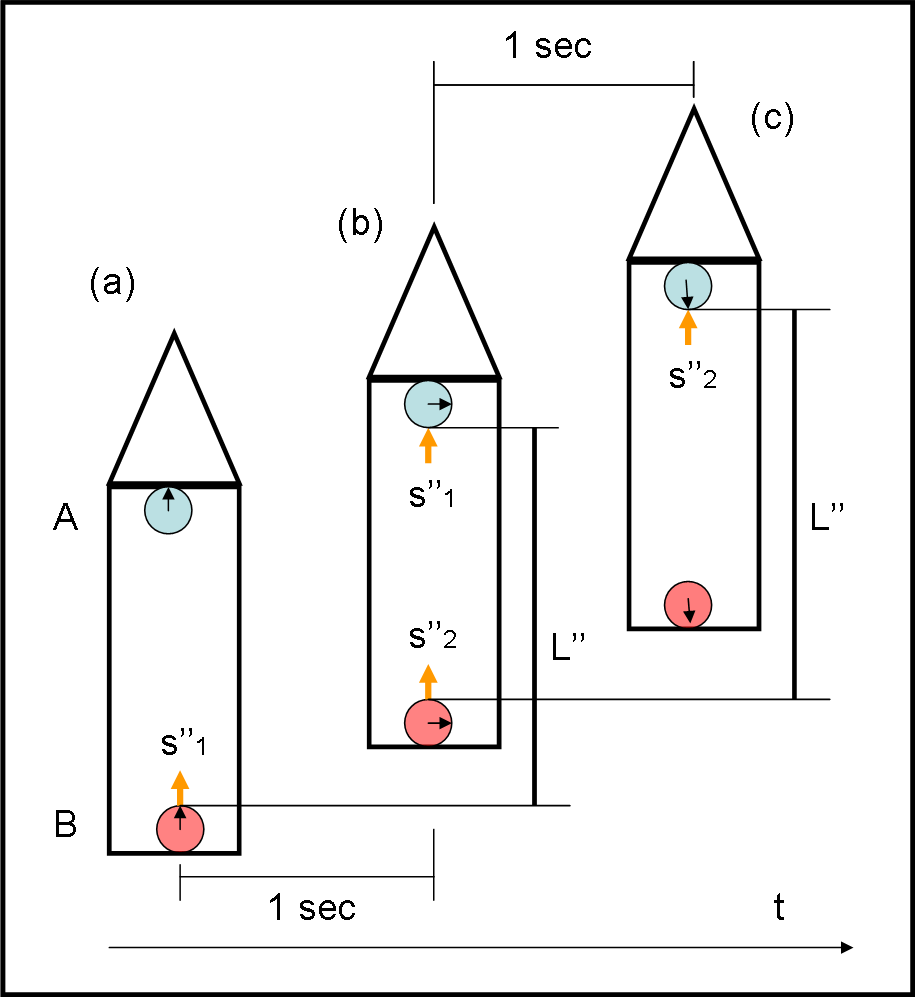
Insomma tutto bene, basta ragionarci un po’ sopra. Sì, tutto bene se … non ci fosse il principio di equivalenza.

Accidenti… se questo capita in un’astronave accelerata, deve anche capitare in un campo gravitazionale: l’orologio più alto deve girare più velocemente di quello più in basso!

E questo è un fenomeno perfettamente uguale a quello che succedeva nello spazio della strana piastra calda. Più ci si allontanava dal centro e più la lunghezza del righello unitario aumentava. In questo caso più si va lontano dalla massa (chiamiamola pure “piastra”) e più l’orologio gira veloce, ossia il tempo misurato risulta più lungo.

Einstein era talmente sicuro del suo principio di equivalenza che non poteva fare altro che accettare il fatto che gli orologi misurano un tempo diverso ad altezze diverse dalla Terra. Non solo gli orologi, ma anche i battiti del cuore e tutti i fenomeni fisiologici…

Solo un genio, sicuro di sé, poteva proseguire lungo questa direzione che sembrava un’assurdità perfino più grande del mondo di Alice. Einstein lo fece e gli esperimenti gli continuano a dare ragione. Lo spazio e il tempo, ossia lo spaziotempo è curvato dalla gravità.

Abbiamo visto che una piastra molto strana (definita attraverso la sua massa/energia) causa uno spaziotempo curvo. Basta allora scrivere la relazione che vi è tra le caratteristiche della curvatura e le caratteristiche della piastra. Questa relazione prende il posto della ben più famosa F = ma.

Come sempre, la verità è di una semplicità disarmante… la difficoltà sta nello scriverla in un linguaggio comprensibile agli umani. L'Universo la conosce e la segue perfettamente.

Un attimo di riflessione e di ... ripasso elementare

Potremmo andare avanti nella descrizione della relatività generale (RG) utilizzando qualche formula in più (senza esagerare, ovviamente) e arrivare abbastanza velocemente (non dimostrando proprio tutto) a esprimere in linguaggio matematico (e fisico) la teoria che la riassume. In fondo, i punti essenziali li abbiamo già toccati e spero, anche, in modo abbastanza comprensibile.

D’altra parte, la RG spiega il tutto (o quasi) e non sarebbe giusto se fosse a conoscenza solo di pochi eletti. Se spiega il tutto (o quasi) deve essere compresa da TUTTI (o quasi).

Tuttavia, dato che non possiamo svilire più di tanto il lavoro di Albert (anni e anni di sofferenza, di delusione e di lampi di genio apparentemente assurdi), è giusto cercare di capire meglio la situazione a cui siamo arrivati e nel contempo renderci conto delle difficoltà potenziali da superare per sostituire alla semplice legge di Newton un qualcosa di ben più generale che riesca a non fermarsi di fronte a corpi celesti con proprietà fisiche ben diverse da quelle del nostro piccolo mondo quotidiano.  Lo faremo, ma cercando di portare più avanti possibile, insieme a noi, anche i meno preparati e i più piccoli.

Coloro che non hanno avuto problemi fino a questo punto, possono anche saltar questo capitolo o al limite usarlo solo come un  facile ripasso. Per gli altri può essere un modo per chiarirsi meglio le idee.

Speriamo anche che questi tentativi continui  di semplificazione servano agli insegnati e li stimolino a riflettere sulla RR e sulla RG, soprattutto. La più grande rivoluzione scientifica ha ormai cent’anni, eppure nelle scuole non si insegna. E non si dica: è cosa per pochi eletti. Assolutamente no: tutto ciò che spiega la realtà deve essere alla portata di tutti, dato che tutti facciamo parte della realtà. Basta studiare, capire, smussare gli angoli e divulgare. Buona scuola vuole anche dire buoni insegnanti! Inoltre, Einstein ha sempre usato ragionamenti quasi infantili, nella loro semplicità.

Iniziamo con qualche riflessione di carattere generale…

Ricordiamo che Einstein non aveva la possibilità di ottenere osservazioni sui giganti cosmici e quindi la parte più essenziale della sua teoria era nascosta completamente (o quasi) dalla limitatezza delle osservazioni terrestri. Non per niente, furono altri scienziati a dedurne le infinite applicazioni che ancora oggi portano a continue conferme.

E’questa la grandezza suprema dell’intera faccenda. Poter lavorare solo su un paio di numeri interi e piccoli e riuscire a ragionare in termini giganteschi, che solo i computer possono oggi regalarci. Facciamo un esempio… il calcolo di un’orbita era già possibile ai tempi di Keplero, ma nessuno poteva certo pensare di arrivare a calcolare il viaggio di una navicella spaziale sotto l’effetto delle innumerevoli perturbazioni planetarie. C’era la potenzialità, ma per riuscire a farlo bisognava ancora scrivere tutta la meccanica celeste. I pianeti e i satelliti erano lì, con i loro movimenti, con una loro storia passata e futura. Tuttavia, la meccanica celeste doveva fermarsi e attendere i computer per prevedere o ricordare gli eventi dinamici accaduti nel nostro sistema planetario su tempi scala delle decine di milioni di anni.

Einstein ha fatto qualcosa di molto diverso. E’ come se fosse stato un Keplero in grado di scrivere una formula senza confini, né verso l’infinitamente piccolo (magari, prima o poi, con l’aiuto della meccanica quantistica arriverà al “nucleo” di tutto), né verso l’infinitamente grande. Bastava fare i calcoli e aspettare che l’uomo fosse in grado di misurarli nella realtà dell’Universo. Esattamente il contrario di quanto normalmente succede (o dovrebbe succedere) nella Scienza.

Galileo ne sarebbe fiero e un po’ imbarazzato. E’ vero che il suo illustre collega si basa, in fondo, sull’osservazione della realtà, ma i suoi voli di fantasia e di estrapolazione vanno ben oltre il suo metodo scientifico. Anzi, sembrano di una libertà mentale troppo rischiosa e fondata solo su idee e non fatti.

Forse è stato proprio Einstein a lanciare la moda delle teorie più astruse sull’Universo, la sua nascita e il suo evolversi. L’unica differenza sta nella qualità del cervello e nelle possibilità deduttive. Lui poteva permetterselo perché vedeva dove nessuno riusciva a vedere, inquadrava logicamente ciò che sembrava completamente slegato. Ma, soprattutto, non temeva le prove osservative, anzi le sperava, tanto era la sua fiducia nel quadro che aveva completato. Oggi, le teorie più astruse nascono, il più delle volte, proprio perché sarà probabilmente impossibile verificarle.

Sicuramente (ma non ne sono tanto sicuro) si riuscirà a migliorare la relatività generale e il cammino da percorrere è quello aperto, anzi socchiuso, dalla meccanica quantistica, ma bisognerà aspettare qualcuno che faccia sua la concezione generale di Einstein e che abbia le sue stesse capacità deduttive: un nuovo bambino che capisca e parli il linguaggio del Cosmo.

Ecco perché, spesso e volentieri, divento una furia quando sento perfetti ignoranti, senza alcuna base fisica, senza apertura mentale e senza una minima visione generale di quanto sia complessa, armoniosa, poetica, artistica e… semplice la teoria del grande Albert, proporre cambiamenti, sollevare critiche, suggerire teorie che contengono grandezze e particelle che nemmeno sanno cosa siano. Il loro luogo di azione non è l’articolo scientifico pubblicato e libero di essere valutato… no, il loro mondo vuoto e squallido è il “forum”, dove tutti possono dire tutto senza nemmeno pensare a studiare, a riflettere e a rischiare veramente in prima persona.

Ma torniamo a noi e alla nostra teoria che ci sta aprendo le porte delle sue meraviglie. Meraviglie che, purtroppo, saremo solo in grado di osservare da lontano, di apprezzare superficialmente, sapendo che certi segreti ci sono ancora vietati nei loro risvolti più sottili e brillanti. Tuttavia, è già un grande risultato, una grande conquista del pensiero e della conoscenza. Il piacere è comunque assicurato, se tenuto a freno da una sana e indispensabile umiltà scientifica e culturale.

Ho parlato senza freni e senza direzioni prescelte… sono andato dove mi portava il cuore. Adesso, però, è ora di tornare a noi e cercare di capire sempre meglio l’essenza dell’opera d’arte, osservandola nel suo insieme e nelle sue finalità più generali.

La cosa migliore è iniziare da un confronto terra-terra tra ciò che diceva Newton e ciò che dice Einstein, con tutto il più grande rispetto e gratitudine per il suo sconfinato maestro.

Gravità = curvatura spaziotempo

Questa è l’uguaglianza fondamentale, da tradurre in una teoria che cambi completamente la concezione del Cosmo.

Cominciamo dalla descrizione della curvatura. Non è certo cosa semplice. Noi l’abbiamo fatto con una superficie sferica e già ci sembra di essere andati lontano, superando non pochi scalini legati alla realtà quotidiana. La curvatura di cui si ha bisogno, a parte la sua struttura spaziotemporale e non solo spaziale, è decisamente variabile e difficilmente calcolabile (lo vedremo più in là).

Tuttavia, può venirci in aiuto, per comprendere almeno le difficoltà intrinseche, fare un confronto con gli effetti derivanti dalla gravità newtoniana. Ciò che si trova nella teoria di Newton deve essere presente anche nella Relatività. Le due cose devono essere del tutto equivalenti! Vogliamo o non vogliamo dimostrare che tutti gli effetti conosciuti da Newton sono dovuti a qualcosa di nettamente diverso, ma che li spieghi perfettamente? E allora affrontiamo gli ostacoli che ci prospetta Newton e trasferiamoli alla curvatura.

Andiamo avanti con i piedi di piombo… E teniamo ben presente che ormai siamo costretti a pensare sempre in termini di spaziotempo, come ci ha dimostrato benissimo quella piastra così strana che deforma lo spaziotempo attorno a lei. Non parliamo più di massa o di densità della materia (cosa, comunque, decisamente migliore), ma pensiamo a un qualche strano macchinario che Einstein ha già preparato adeguatamente attraverso la sua dinamica relativistica. Massa ed energia, ricordate? Anche questo sarà un punto complesso da definire: un marchingegno che sia in grado di deformare lo spaziotempo… e dico poco!

Facciamo, allora un passo indietro per riassumere ciò che abbiamo dimostrato fino ad ora. Non siamo molto lontani dalla fine, se escludiamo la traduzione in linguaggio matematico.

Prepariamo uno schema veramente elementare che ci faccia posare i piedi per terra (anzi librare nello spazio) e capire esattamente con cosa abbiamo a che fare. Può sembrare una pagina di un libro da scuole elementari. Qualcuno, forse, si rifiuterà di leggere, pensando che le sue conoscenze siano ben superiori. Noi, e io per primo, ci troviamo, invece, a nostro agio, dato che di fronte al genio di Newton e di Einstein, non possiamo che sentirci bambini con la bocca semiaperta per lo stupore.

Per rendere il tutto ancora più infantile vorrei introdurre un personaggio che ci aiuterà a capire dove ci stiamo trovando. Forse, ci aiuterà a portarci dietro, nel nostro viaggio, anche i veri bambini. Un personaggio femminile, però. E’ora di non limitarci più a scienziati, ad astronomi, a studiosi, in genere. Probabilmente chi farà il passo successivo verso l‘unione totale di mondo relativistico e quantistico sarà una donna, dotata di una fantasia e di una sensibilità sottile che gli uomini non hanno. La chiamiamo ISALBA (l’etimologia del nome non è difficile da comprendere) e ve la presento nella Fig. 17.

Come vediamo, Isalba è munita di un righello e di un orologio, più che sufficienti per insegnarci la strada da seguire. In fondo, li conosciamo già (ricordate la prova di esame di Einstein e Newton QUI, fig. 13 e 14?). D’altra parte vogliamo entrare nello spaziotempo e un righello per misurare le distanze e un orologio per misurare il tempo sono sufficienti. Immaginiamo che vi siano un certo numero di Isalbe sparse nel vuoto del Cosmo.

Fermi tutti, sappiamo benissimo che il vuoto non è veramente vuoto, ma per adesso possiamo facilmente soprassedere. Vuoto, vuoto… sembrerebbe qualcosa che non esiste e non può esistere. In realtà, è meglio cambiargli nome e chiamarlo proprio spaziotempo. Lo possiamo anche definire come struttura atta a essere misurata in qualche modo. Se non si misura, lo spazio cessa di esistere e se l’orologio non si muove il tempo non passa.

Questo è il ragionamento di fondo. Lo spaziotempo, quindi, è un qualcosa che ha senso solo se si riesce a misurare attraverso una certa geometria con un numero qualsiasi di dimensioni. Noi viviamo in uno spazio a quattro dimensioni e la sua geometria comprende anche il tempo. E’ ovvio, quindi, che Isalba si sia munita di un righello e di un orologio… senza di loro lo spaziotempo non esisterebbe e lei (come tutti noi) non potrebbe entrarci.

Invece vediamo con piacere che si trova a suo agio e quindi vuol dire che lo spaziotempo esiste ed è, conseguentemente, misurabile (ma vale anche il viceversa).

Le nostre Isalbe, in Fig. 18, si divertono, perciò, a misurare distanze, a segnare intervalli di tempo, a scoprire le dimensioni in cui sono immerse.

Possiamo anche dire, con una certa sicurezza, anche perché siamo in una piccola regione di spaziotempo, che i righelli e gli orologi funzionano perfettamente e vanno in perfetto accordo. Ci lanciamo a dire una parola difficile: lo spazio è euclideo! Sappiamo bene cosa vuol dire, ma è sempre meglio richiamarlo. Esso è misurabile attraverso la geometria euclidea, ossia si può applicare il teorema di Pitagora, le rette parallele non si incontrano mai, la somma degli angoli interni di un triangolo è 180 gradi, ecc., ecc. In ogni modo, le caratteristiche di uno spazio euclideo e di uno spazio curvo le abbiamo analizzate a lungo QUI.

Le nostre simpatiche amiche stanno costruendo lo spaziotempo, proprio perché lo spaziotempo è un qualcosa che serve a dirci dove siamo. Ognuna di esse rappresenta un evento, ossia ha una certa posizione in un certo istante (l’analogo del punto nello spazio a tre dimensioni).

Per non rischiare di creare confusione, diciamo subito che Isalba non si muove rispetto alle altre. Se lo facesse rischierebbe di entrare in crisi profonda: le misure di spazio e tempo cambierebbero e le nostre amiche non andrebbero più d’accordo.

Basterebbe spiegarle che esiste la relatività speciale e loro capirebbero cos’è quella strana apparenza che hanno i righelli e gli orologi se visti da Isalbe diverse, in moto uniforme una rispetto all’altra.  Ma noi queste cose le sappiamo già e sappiamo anche bene come tutto sia perfettamente simmetrico, per cui possiamo, almeno per il momento, escluderle dal nostro discorso. Noi siamo interessati a qualcosa che capiti solo in certe condizioni e che tutti possano vedere e confermare. Qualcosa di “assoluto” (occhio che ciò non è in effetti possibile) e non di soggettivo.

Ed ecco che nel nostro spaziotempo compare un “qualcosa”. Newton la chiama massa, Einstein la definisce in modo più complesso e pensa a lei come a un marchingegno in cui materia ed energia diventino una sola cosa. Per adesso, comunque, non c’interessa più di tanto. Passiamo alla Fig. 19.

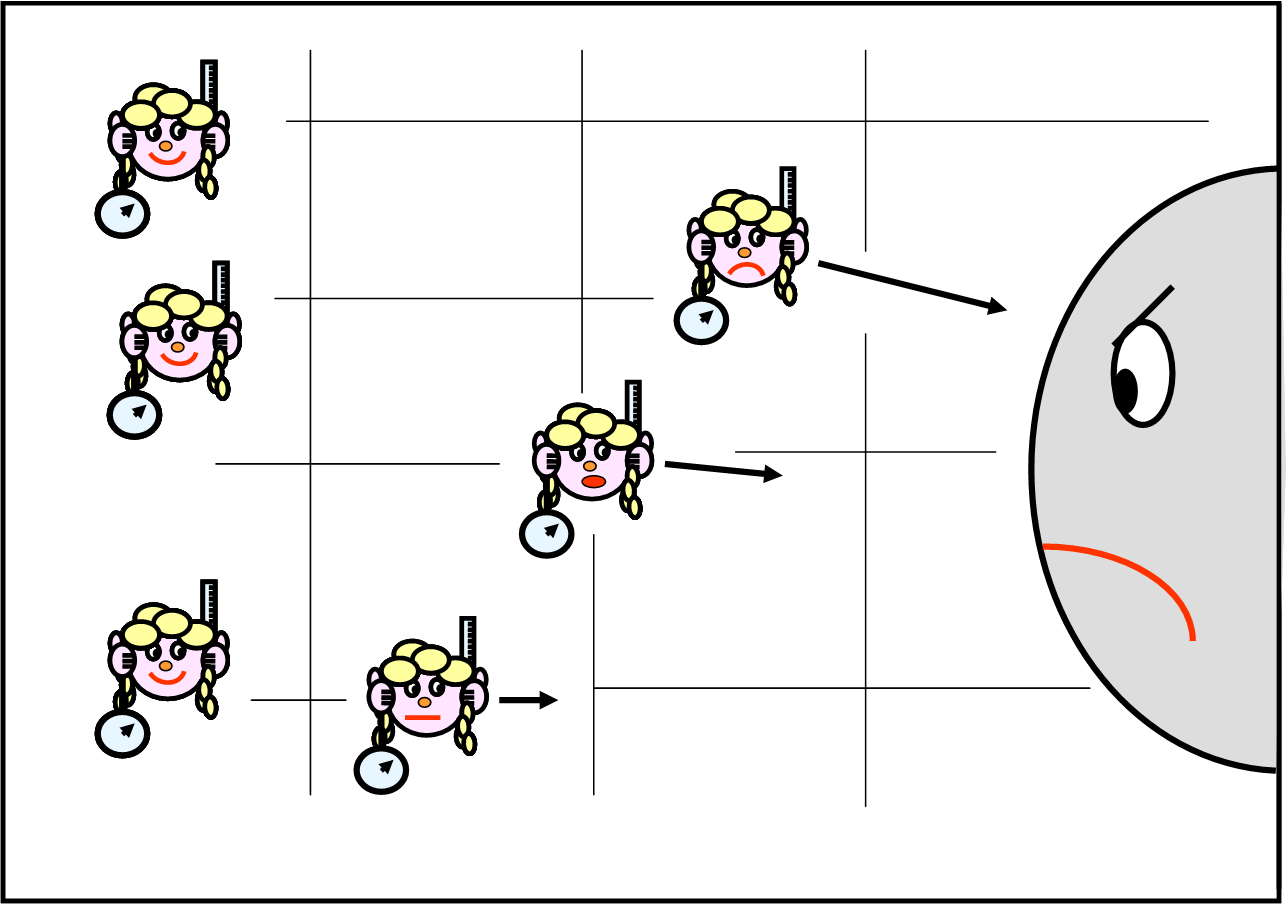
La presenza di questa “massa” (chiamiamola così per semplicità) sta modificando le azioni di Isalba e delle sue compagne, in modo inaspettato. Righelli e orologi funzionano ancora? Sembra di sì, almeno a prima vista. Cosa sta succedendo allora? Bene, le Isalbe più vicine alla massa si sentono trascinate verso di lei in modo violento, mentre quelle più distanti lo fanno in modo meno violento. Chi è ancora più lontana non se ne accorge nemmeno.

Non è difficile disegnare vicino a ogni Isalba una piccola freccia che indichi il loro movimento o, se preferiamo, velocità (variazione dello spazio percorso in funzione del tempo). Ci accorgiamo che questa velocità cambia in modo tale, però, che la sua variazione (accelerazione) rimanga costante. Che cos’è che tira verso di sé le Isalbe? Non esiste corda nello spazio (possiamo parlare solo di spazio, essendo nel mondo newtoniano) e la colpa deve essere di quella massa comparsa dal nulla. Essa deve essere capace di spostare le “cose”  anche senza toccarle.

Una maga in piena regola, una maga che segue una legge piuttosto semplice: chi è più vicino viene tirato di più. Siamo di fonte a una vera caduta “libera” verso un qualcosa che agisce nello spazio. Lo spazio, allora, non è solo un vuoto che esiste perché è misurabile, ma è un qualcosa che ammette poteri magici che agiscono a distanza. Diamogli un nome: forza o campo o quello che vogliamo. Non si possono toccare, ma esistono e si vedono chiaramente attraverso i loro effetti sulle nostre Isalbe.

Nel frattempo è comparsa un’altra massa, ancora più potente. Per definire cosa sia più massiccio di un’ altro, Isalba ha bisogno di altri strumenti oltre che al righello. Quest’ultimo le può solo dire chi è il più grande, come dimensioni spaziali, ma si rende conto che non basta. A parità di dimensioni una massa è più massa di un’altra… in poche parole, cambia la densità della materia che riempie il volume misurato con il righello. Einstein, frattanto, se la ride… dato che il suo marchingegno si basa essenzialmente sulla densità.

Ma torniamo al mondo newtoniano. Ci siamo accorti che la magia che attira le cose dipende anche dalla massa della cosa che è apparsa dal nulla. Più ne ha e più gli effetti magici sono importanti ed evidenti. Tuttavia, scopriamo anche un'altra cosa fondamentale: le Isalbe cadono tutte con la stessa velocità, se si trovano alla stessa distanza dalla massa, indipendentemente da quanto siano massicce loro stesse.

E qui, forse, Newton avrebbe già dovuto pensare che qualcosa non andava bene nella sua descrizione. Perché mai la massa di chi subiva non contava assolutamente niente nel fenomeno magico? La spiegazione era di comodo: la massa giocava un doppio ruolo, quello di resistere e di cedere alla massa preponderante. In parole più tecniche, la massa m che compare nella legge di gravitazione universale (F = GMm/r²) è la stessa che compare nel secondo principio della dinamica (F = ma).

L’unico problema era che se qualcosa non avesse avuto massa non avrebbe dovuto cadere. Perfetto, almeno fino a che Einstein non è arrivato a cambiare le carte in tavola. Sarebbe stato importante chiedere a una particella piccolissima e mai ferma: il fotone. Lui non ha massa eppure cade come le Isalbe… Ma questo Newton non poteva ancora saperlo.

Attenzione. Sembra che si stia facendo fare a Newton la figura dello sprovveduto. Ci mancherebbe altro (la nostra è solo una favola molto approssimativa): l’uguaglianza tra massa gravitazionale e massa inerziale è un problema ancora al centro di animate discussioni. Einstein non ha fatto altro che … girarci intorno…

Tuttavia, è obbligatoria una considerazione. Einstein non ha, in realtà, sfruttato le osservazioni dell’Universo per mettere in discussione la visione di Newton. Più o meno le conoscenze erano le stesse. La sua teoria, perciò, non nasce da evidenze osservative, ma da una visione mentale diversa. Una visione assurda, strabiliante e rischiosissima per la sua stessa reputazione scientifica.

E’ giunta, finalmente, l’ora di guardare, con più attenzione (Fig. 20), cosa stanno facendo le nostre amiche che stanno cadendo per magia verso la massa. Accidenti, lavorare attorno a un pianeta “piccolo” come la Terra comporta grandi problemi. I righelli e gli orologi sembravano sempre gli stessi e invece…

Einstein vede (anzi, immagina soltanto, ma ha pienamente ragione) che i righelli si accorciano mentre le nostre amiche cadono verso la massa. Non solo, però, anche i loro orologi girano sempre più lentamente (ossia il tempo misurato diminuisce). Quella che sembrava una magia che operasse all’interno dello spazio (e il tempo) sembra essere proprio una modifica dello spaziotempo.

La massa, o chi per lei, deforma la geometria con la quale le nostre amiche erano riuscite a misurare distanze e tempi. Le regole della geometria euclidea non valgono più e bisogna utilizzare quelle “strambe” di una superficie curva.

Abbiamo già visto come una piastra molto speciale possa riuscire a fare questo e ora Isalba e compagne lo toccano con mano. In realtà chi sta cadendo non se ne può accorgere, dato che per lei nulla cambia. Ma chi sta fuori dalla mischia lo può notare facilmente, dovunque si trovi. Einstein è riuscito a mettersi in quelle condizioni! E’ riuscito a dimostrare una curvatura intrinseca nelle quattro dimensioni senza poter passare in una dimensione superiore. Meraviglioso, meraviglioso!

Ma, allora, tutto può cambiare e diventare addirittura più semplice. Non c’è nessuna forza magica che attira le cose (o almeno non nel senso che Newton aveva pensato), ma è lo spaziotempo deformato che costruisce strade speciali per condurre Isalba e le amiche verso la massa o la piastra o quello che preferite.

Siamo in uno scambio ferroviario, dove ogni linea ferroviaria viene incanalata verso la stazione centrale (la massa). Un binario, però, non cambia a seconda del treno che arriva: la stessa linea verso la stazione può essere seguita da un freccia rossa o da un regionale. In altre parole, è ovvio che la massa di chi cade non conti più! Giunti nella periferia di una grande città (una grande piastra) ogni treno (Isalba) segue la linea più “rapida” per arrivare nella stazione centrale. Il rapida assume però un significato diverso, proprio perché le caratteristiche dello spaziotempo non sono euclidee. Ma ci torneremo presto… Ci basti dire (come già accennato) che la linea da seguire (la più corta) è quella che corrisponde al tempo più lungo. Nel nostro mondo euclideo la verità è proprio il contrario: la strada più corta è quella che è percorsa nel tempo minore

Questa è la realtà dello spaziotempo. Esso non è una struttura fissa e inamovibile come un teatro in muratura. Esso è un qualcosa che localmente si può sbizzarrire ad assumere “forme” diverse, variabili, curve o quello che preferiamo usare come analogia. Una vera e propria creatura, simile a un mollusco, che cambi forma, si incurvi, si dilati, si contorca. Addirittura, tutto l’Universo potrebbe risentire di queste variazioni locali… da cui la famosa “forma” dell’Universo (QUI)

Accidenti, ma era così semplice… altro che magia… è solo questione di strade e di ferrovie che permettono gli spostamenti nello spaziotempo. Peccato che nessuna osservazione poteva confermarlo e ci sono voluti anni per dimostrare che la soluzione di Einstein era quella giusta (e quindi niente Nobel per la più straordinaria teoria della Scienza macroscopica). Teoria che giorno dopo giorno ottiene nuove conferme (buchi neri, onde gravitazionali, ecc. ecc.).

La RG è tutta qui. Bisogna solo scrivere una relazione tra curvatura e piastra. E qui le cose si complicano. Einstein ha saputo cercare e capire. La descrizione di una curvatura variabile, a quattro dimensioni, era già stata elaborata. Così come la sua dinamica relativistica era in grado di costruire una piastra capace di deformare lo spaziotempo. Bastava eguagliare due espressioni e tutto si risolveva.

Qualcuno, ogni tanto, dice che Einstein ha approfittato degli studi degli altri (Lorentz, Ricci, ecc.). Sicuramente ha utilizzato qualcosa di conosciuto, studiandolo e capendolo a fondo (e questo la dice lunga sulla sua umiltà culturale), ma ha saputo genialmente adattare qualcosa di puramente teorico a qualcosa di eccezionalmente pratico. E poi, cari amici, legare curvatura con masse ed energia è pur sempre un’idea che poteva venire solo a lui. Eppure, era proprio quella giusta.

Tra parentesi, una piccola chicca… Sembrerebbe che Einstein abbia risolto brillantemente il fatto che il fotone cada anch’esso verso la stazione attraverso una rete ferroviaria. Massa o non massa, i binari sono quelli. Tuttavia, a voler essere sinceri, la deformazione dello spaziotempo è pur sempre un qualcosa di “attrattivo” (le masse cadono verso qualcosa) e la massa del treno gioca la sua parte.

Il non avere massa darebbe comunque grossi problemi interpretativi. Ma Einstein ha risolto quasi automaticamente questo “problemino”. Ricordiamo che il fotone non ha massa a riposo, ma ha energia (e qui la MQ si affaccia alla grande) e quantità di moto (deve averla per forza visto che non sta mai fermo!). Tuttavia, la massa non è altro che la quantità di moto divisa per la velocità. E allora, eccoci servita su un piatto d’argento una strana massa relativistica del fotone che lo fa diventare un treno vero e proprio.

Non proveremo nemmeno a entrare nel mondo dei tensori e nei risvolti più sottili della formula generale della RG (semplicissima all’aspetto, ma…). Di sicuro analizzeremo meglio che tipo di curvatura abbiamo di fronte avvicinandoci alla piastra. Noi abbiamo sempre parlato di “curvatura” media, ma la curvatura di cui abbiamo bisogno è ben più complessa (non per niente Einstein ha dovuto cercare e ricercare per trovarne una descrizione soddisfacente). Ci limiteremo ad alcuni effetti di curvatura che sono sotto gli occhi di tutti (si fa per dire). Newton non li aveva considerati ma esistevano anche lavorando solo con la sua teoria… D’altra parte la RG deve risolvere tutto ciò che trovava e spiegava Newton: la realtà è quella e una teoria non può mai cambiare la realtà.

Qualche formula e il gioco è fatto

Siamo giunti alla formula risolutiva, a quella che lega curvatura con massa/energia. Curvato il tempo, dovremo affrontare una piccola lotta tra RR e RG per descrivere il moto di tutto ciò che finisce nei pressi di una massa con una densità importante. Anche la luce deve inchinarsi alla legge forse più rivoluzionaria della Scienza.

Cerchiamo di quantificare in modo molto semplice la “curvatura” del tempo, collegata ovviamente a quella dello spazio (la Relatività Ristretta non perdona e ci torneremo al momento giusto).

Torniamo sulla nostra astronave  con i due orologi in A e B (Fig. 13). Consideriamo come buona la formula che regala l’effetto doppler relativistico (prima o poi la ricaveremo, ricordando però che parliamo di un vero effetto doppler e non di uno spostamento verso il rosso, ossia è il classico effetto doppler ma con una velocità di spostamento della sorgente che sia comparabile con quella della luce). Essa dice:

f  = fo (1 + v/c)/(1 - v²/c²)          …. (1)

dove fo e f sono le frequenze misurate alla partenza dall’emettitore e all’arrivo al ricevitore. In realtà, nel nostro caso, le velocità dell’emettitore e del ricevitore sono uguali (sembrerebbe che non ci sia velocità della sorgente rispetto al ricevitore). Ciò non è, però, vero… dato che l’astronave accelera e quindi durante il viaggio della luce da A a B (H) vi è un aumento di velocità data da gt dove g è l’accelerazione e t è il tempo impiegato ad andare da A a B. Il tempo t può essere approssimato da H/c. Ne segue che quando il segnale arriva in B, la velocità dell’astronave è aumentata del valore:

gt = gH/c

Questa è sempre la velocità relativa tra ricevitore ed emettitore e può quindi essere considerata come la velocità di spostamento da inserire nella (1). Considerando molto piccole la distanza H e l’accelerazione g, v risulta decisamente minore di c e possiamo trascurare nella (1) il termine v²/c².

La (1) diventa:

f = fo (1 + gH/c²)      …. (2)

In parole: la frequenza dell’orologio del ricevitore è uguale alla frequenza dell’emettitore moltiplicata per la quantità:

(1 + gH/c²)

Per il principio di equivalenza, tutto ciò che capita in un astronave che ha un accelerazione -g, deve capitare anche in un campo gravitazionale che ha un’accelerazione di caduta libera uguale a g.

La relazione (2) si può anche dimostrare in altro modo. Il fotone parte dall’orologio superiore con una certa energia data da:

 E_A = fo h

 Dove h è la costante di Planck e fo la frequenza del segnale alla partenza.

 La sua massa relativistica (l’abbiamo spiegata nella parte finale di questo articolo) è:

 m_F = E_A/c²

 m_F = fo h/c²

 "cadendo” verso la terra (l’accelerazione dell’astronave è equivalente a una caduta verso terra a causa della gravità) si recupera l’energia potenziale tra A e B. Essa vale:

 E_AB = m_F g H     (H è la distanza tra A e B)

 All’energia del fotone “in caduta” si deve aggiungere questa energia e si ottiene:

 E_TOT = E_A + E_AB  = fo h +  m_F g H  =  fo h + fo hgH/c² = fo h(1 + gH/c²)

 Tuttavia, E_TOT non è altro che l’energia che arriva in B che è data da :

 Etot = E_B = f  h

Dove f è la frequenza, ovviamente cambiata. Si ha subito il rapporto tra le due frequenze, quella di ricezione e quella di emissione:

 f  h = fo h(1 + gH/c²)

 f = fo (1 + gH/c²)         …. (2)

Tutto ciò in perfetto accordo con quanto rilevato dagli orologi. Quello in B vede la frequenza dei segnali inviati da A più alta. Ossia, quello in B è più lento. Ma, adesso, abbiamo anche quantificato il fattore di rallentamento attraverso le frequenze.

La strana “piastra” curva lo spaziotempo

Abbiamo già capito che tutto ciò che comporta una differenza di tempo in zone diverse è analogo a quanto avevamo trovato per una piastra che scalda al crescere della distanza. Ma il risultato è ben più che un’analogia: lo spaziotempo è proprio curvo. Vediamolo meglio con una semplice serie di figure nello spaziotempo. Figura che abbiamo usato spesso e volentieri, considerandole figure essenzialmente geometriche. In ascissa c’è lo spazio e in ordinata il tempo.

Cerchiamo di costruire un rettangolo in questo sistema di coordinate. Il nostro spaziotempo (un solo sistema di riferimento) è immerso in un campo gravitazionale. Partiamo da un punto B e immaginiamo che sia fermo. Esso segue la sua linea di Universo parallela all’asse del tempo. Questo “lato” del rettangolo valga esattamente 100 sec (del suo tempo proprio, ovviamente). Il primo lato è quindi BD (Fig. 21a)

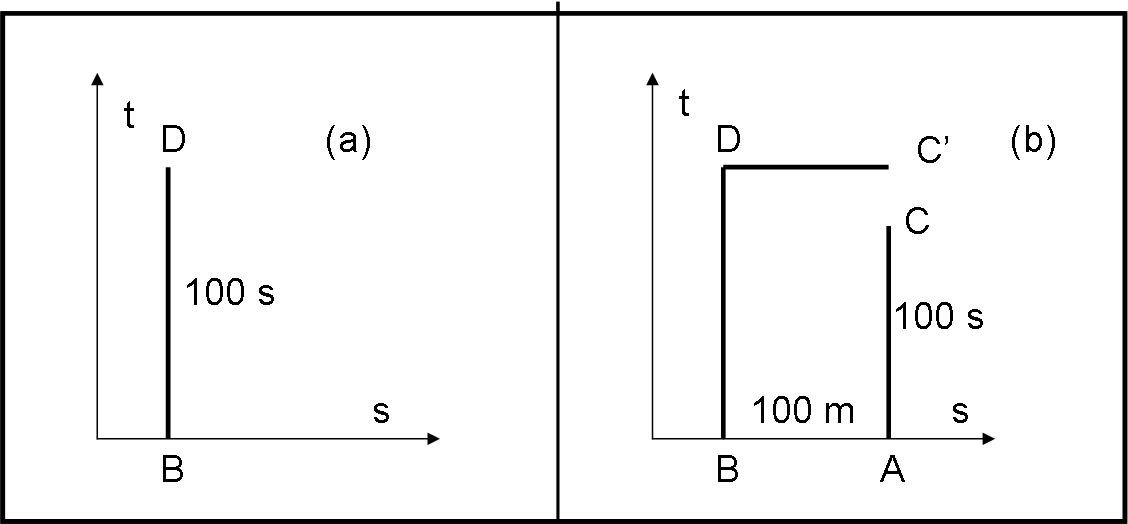
Prendiamo adesso un altro punto A che stia a 100 m di distanza da B. Immaginiamo che anch’esso sia in quiete. Misuriamo nuovamente 100 sec con il suo orologio e ci fermiamo nel punto C corrispondente. Abbiamo appena dimostrato, però, che due orologi posti a una certa distanza (altezza) tra di loro (A è più ALTO di B nel campo gravitazionale) girano in modo diverso. In particolare, A va più veloce di B e raggiunge prima i 100 sec. In poche parole il lato AC è minore di BD. Dobbiamo concludere che i punti C e D NON sono simultanei. Se tracciamo la linea di simultaneità di D (parallela all’asse dello spazio), fino all’oggetto A, essa termina in C’ (Fig. 21b).

Attenzione, siamo in RR, ma non vi è nessun movimento di un sistema rispetto a un altro. Qui siamo in un solo sistema di riferimento: la simultaneità deve mantenersi. Tuttavia, il nostro rettangolo non si chiude, dato che C’ NON coincide con C. Non ci resta che concludere che la geometria del piano considerato non è euclidea, ossia che lo spaziotempo è CURVO.

Vi prego di non considerare banale questa trattazione… Ci siamo messi nello spaziotempo di Minkowski, abbiamo tracciato le linee di Universo di due oggetti FERMI e abbiamo infine considerato la linea di simultaneità. Se il rettangolo spaziotemporale non si chiude vuol dire che lo spaziotempo immerso in un campo gravitazionale è CURVO. Così come succedeva a chi cercava di chiudere un rettangolo su una superficie sferica… ricordate?

Siamo ormai vicini alla conclusione del nostro viaggio (giocoforza semplificato) verso la legge della relatività generale.

Abbiamo, perfino tralasciato di vedere come si comporta la luce in un campo gravitazionale… Bene, lo facciamo subito, utilizzando come al solito la nostra astronave e, poi, il principio di equivalenza…

Anche la luce deve curvare

Che la luce pieghi e tenda a cadere nello spaziotempo curvato, può essere dimostrato in modo estremamente semplice. Torniamo nel nostro razzo che si muove con una certa accelerazione. Noi siamo all’interno del razzo e questo è il nostro sistema di riferimento che equivale (ormai lo sappiamo bene) a un campo gravitazionale.

Qualcuno, esterno all’astronave, spara un raggio di luce che, ovviamente, procede in linea retta, dato che non vi è campo gravitazionale! (Fig. 22).

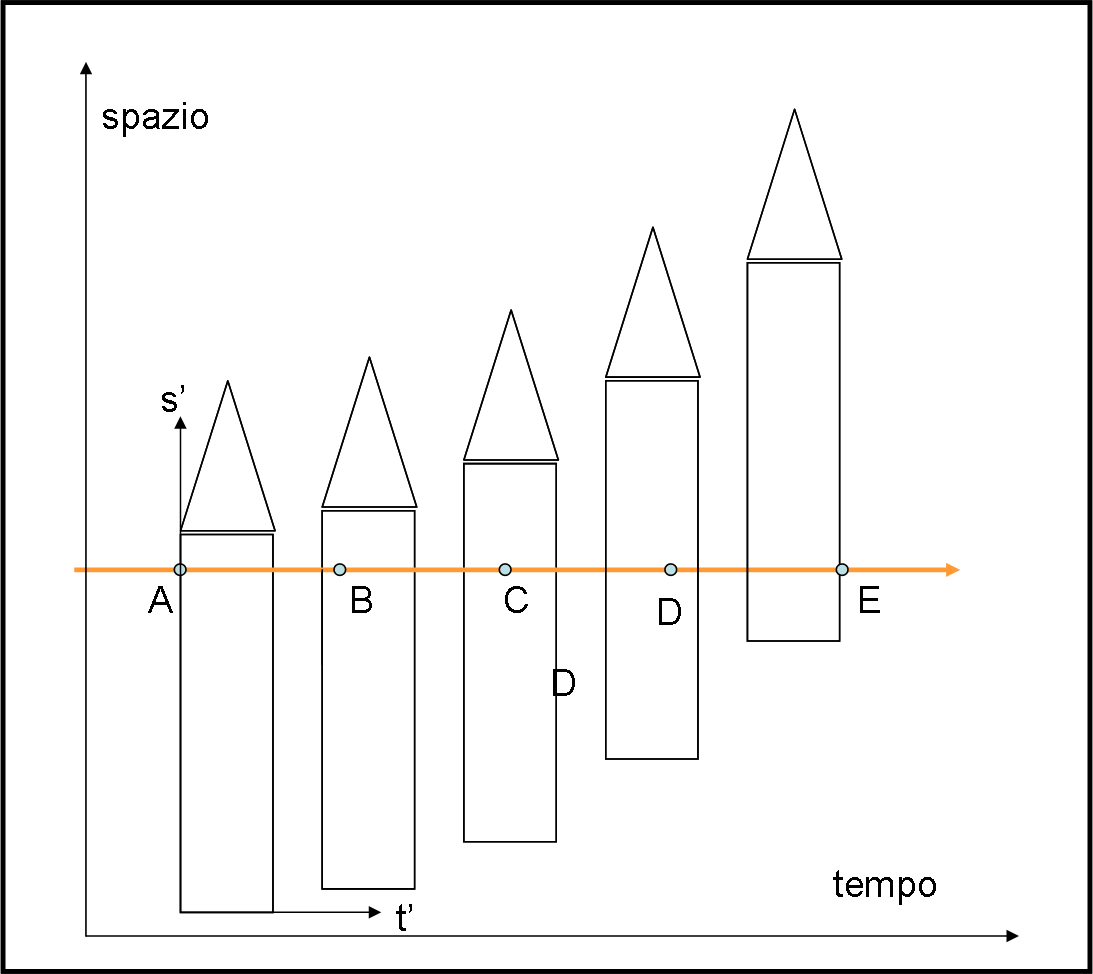
All’istante in cui entra all’interno dell’astronave (immaginata trasparente alla luce) la luce tocca la parte in A. Poi prosegue e giunge in B. Il suo moto sarebbe rettilineo, ma il pavimento dell’astronave si è alzato seguendo la variazione di velocità imposta dall’accelerazione. La stessa cosa succede in C, fino a che la luce esce dall’astronave in E, a un’altezza molto vicina al pavimento.

Per chi è all’interno dell’astronave (Fig. 23), la luce ha compiuto un percorso parabolico (è facile da calcolare), proprio come quello di un qualsiasi oggetto dotato di una certa velocità, immerso in un campo gravitazionale.

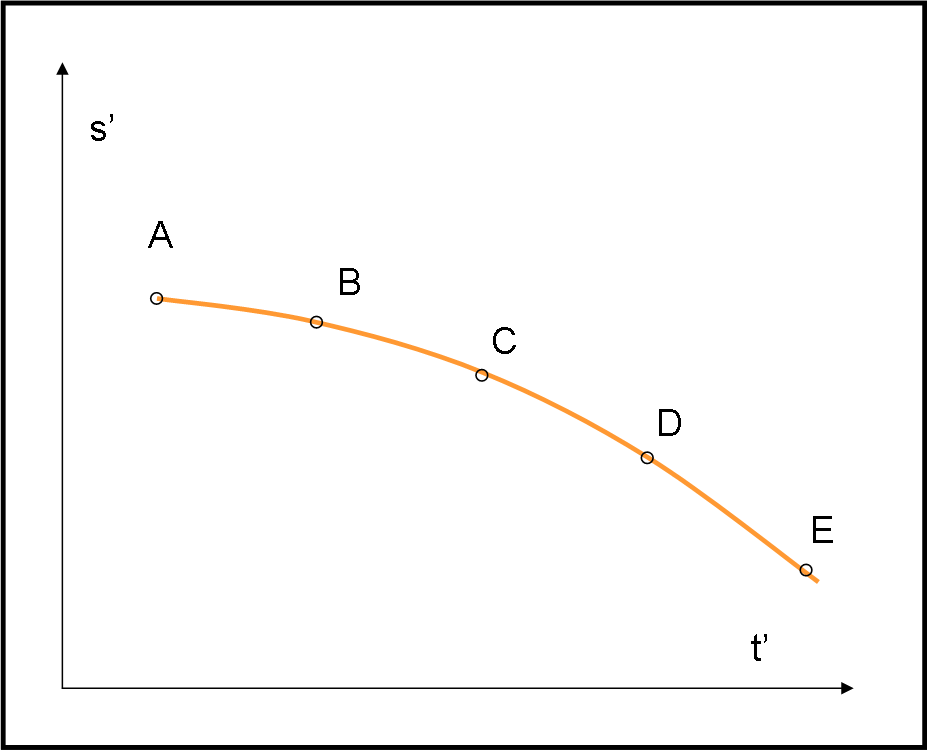
Ma, come ormai sappiamo bene, un’astronave accelerata equivale perfettamente a un campo gravitazionale e quindi possiamo tranquillamente concludere che la traiettoria della luce viene curvata dalla gravità, ossia segue perfettamente i binari dello spaziotempo secondo una traiettoria parabolica.

Uno scontro molto … relativo

Abbiamo fatto esempi molto particolari che ci hanno fatto capire come sia lo spazio che il tempo siano curvati dalla gravità e come perfino la luce sia obbligata a seguire certi binari ben predisposti dalla presenza di una massa. Non possiamo dimenticare, però, che vale comunque la Relatività Ristretta. Essa regala il legame vero che fa dello spazio e del tempo uno spaziotempo. Tutto ciò che agisce sul tempo deve agire anche sullo spazio e viceversa. In poche parole, le due relatività devono convivere. Spesso questa parte fondamentale viene un po’ dimenticata o raggirata. Esse non possono certo scontrarsi o arrivare a conclusioni diverse… Eppure, andando un po’ a fondo, sembrerebbe proprio di sì.

Utilizziamo, tanto per cambiare, una specie di quiz che mette bene in  luce questa ipotetica contrapposizione.

Siamo sulla Terra. Io sono A e l’amico è B. I nostri orologi sono ovviamente sincronizzati. La mia intenzione è di fare “muovere” il mio orologio in modo che dopo cento secondi segni il tempo più lungo possibile. Beh… la cosa è, teoricamente, piuttosto semplice: lo faccio salire fino a una certa altezza, lascio che il mio orologio vada più veloce come abbiamo imparato con la solita astronave, e poi lo faccio scendere in B. Sicuramente dovrebbe segnare qualche secondo in più… E più in alto lo faccio andare e più secondi guadagna (Fig. 24, a sinistra).

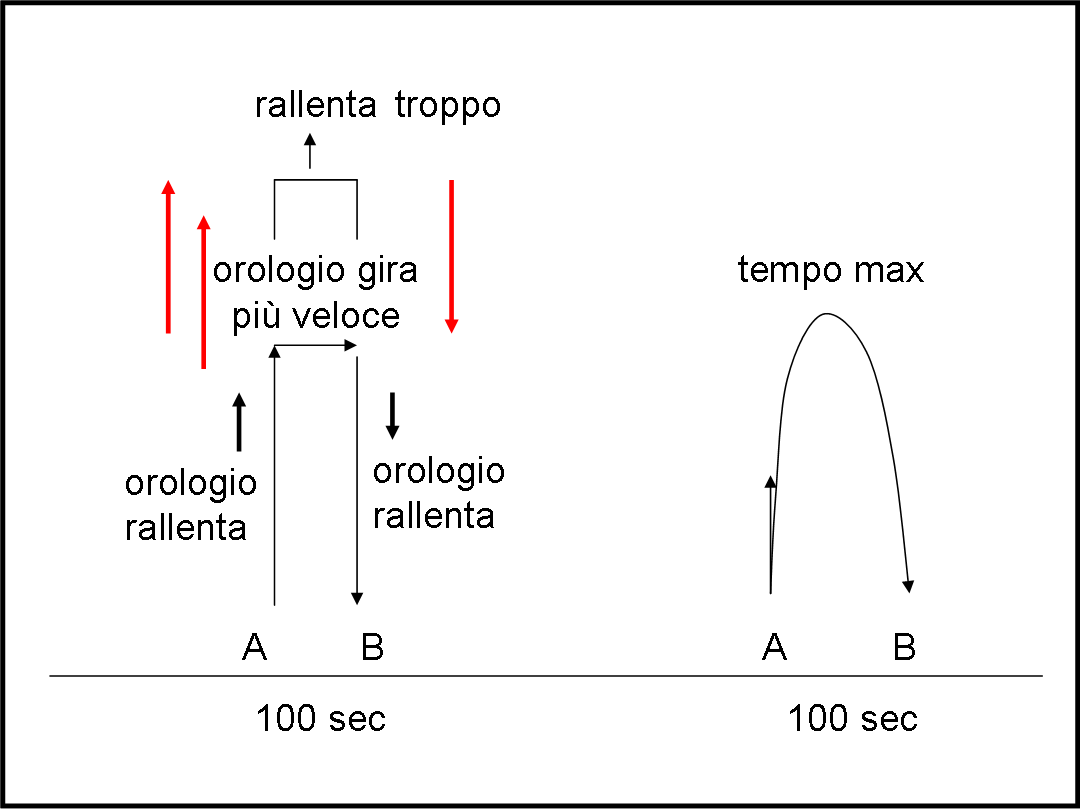
Sì, sì, teoricamente tutto bene. Attenzione però… per raggiungere una certa altezza  devo farlo muovere in qualche modo. Muoverlo, vuol dire impartirgli una certa velocità e per farlo arrivare il più in alto possibile (in modo da guadagnare più secondi) devo utilizzare una velocità molto alta. Ricordiamo, infatti, che il tutto deve compiersi esattamente in 100 secondi dell’orologio B.

E qui nasce un bel problema… Più alta è la velocità e più l’orologio rallenta a causa del "maledetto" fattore di Lorentz! Per diminuire al massimo il tempo del viaggio e sfruttare l’altezza raggiunta sono obbligato ad aumentare la velocità e, conseguentemente, a far rallentare al massimo l’orologio durante il viaggio. La faccenda è decisamente critica: siamo veramente di fronte a una lotta tra RR e RG!

Ricapitoliamo la situazione. Se non muovo per niente il mio orologio esso segnerà 100 secondi esattamente come quello di B. Ma io devo muoverlo (ossia voglio fargli descrivere un moto nel nostro spaziotempo). Se lo mando troppo lentamente in alto riesco a guadagnare qualcosa ma se lo mando troppo velocemente capita il contrario e l’orologio segna meno secondi. Qual è la soluzione più “naturale”?

Nient’altro che lanciarlo verso l’alto in modo che torni nelle nostre mani esattamente dopo 100 secondi. La rapida salita, il rallentamento, la fermata, e la ricaduta a velocità crescente è proprio ciò che ci vuole perché l’orologio misuri il tempo massimo.

Sospendiamo questo interessante giochino e rendiamolo più pratico. Prendiamo due punti A e B sulla Terra e cerchiamo il moto “rettilineo” tra A e B, ossia quello che permetta a un orologio di andare da A a B segnando il massimo tempo possibile. Ricordiamo, infatti, quello che abbiamo detto precedentemente : il moto rettilineo, ossia l’analogo di moto percorso a velocità uniforme, è il moto che obbliga un orologio a spostarsi da un punto in un dato istante (evento 1) a un altro punto in un istante diverso (evento 2), in modo che esso segni il tempo più lungo possibile.

Attenzione, però, questo risultato era stato trovato utilizzando solo la relatività ristretta… bisogna cambiare qualcosetta, adesso, che siamo in un campo gravitazionale.

Combiniamo le relatività

L’idea è quindi quella di aggiustare un po’ il tiro e di non limitarsi alla linea a velocità uniforme. La cosa migliore da fare sarebbe di alzarsi un poco, ma non troppo, in modo da sfruttare al massimo la velocità maggiore degli orologi ad altezze superiori senza fare arrabbiare troppo la RR. Facendo i calcoli si trova nuovamente che la traiettoria ideale è quella parabolica, come, in fondo, abbiamo trovato precedentemente.

La legge del moto in un campo gravitazionale può, perciò, essere così enunciata, in modo generale e tenendo conto di quanto detto precedentemente: “Un oggetto si muove da un punto a un altro in modo che il suo orologio segni il tempo più lungo rispetto a qualsiasi altra traiettoria”. Ovviamente, al di fuori di un campo gravitazionale, la RR torna a giocare da sola, con tutte le sue regole.

N.B.: Utilizzando adeguatamente il diagramma di Minkowski si potrebbe descrivere come un'accelerazione (variazione continua della velocità) si possa inserire  nella relatività ristretta. In poche parole, è come se facessimo variare continuamente il sistema di riferimento in moto. In realtà, la RG potrebbe essere descritta approssimandola punto per punto con la RR. Al momento, però, preferiamo non entrare in dettagli e in trattazioni abbastanza complesse anche visivamente. Digeriamo prima una visione generale della RG. Poi, con calma, potremo anche andarla a sistemare all’interno del nostro diagramma di Minkowski.

Finora, abbiamo usato tante parole che ci hanno dato un’idea qualitativa che a molti potrebbe bastare. Tuttavia, non è molto difficile descrivere il moto nello spaziotempo con qualche formuletta. Newton ne sarebbe sicuramente contento.

La variazione di frequenza dovuta alla gravita è data dalla (2), in particolare al fattore:

fo gH/c²         …. (3)

Dobbiamo, però tener conto che vi è un fattore di segno opposto dovuto alla velocità (fattore di

Lorentz)

f = fo (1 – v²/c²)^1/2     …. (4)

La combinazione della (3) e della (4) porta al risultato voluto.

Noi eseguiamo il calcolo per una velocità v << c.

Ricordando gli sviluppi in serie (vedi lezioni di matematica da n° 43 a n° 50) si ha che:

(1 + x)^1/2 = 1 + ½ x + …

Ponendo

x = - v²/c²

si ha:

(1 – v²/c²)^1/2 = 1 - ½  v²/c²

La (4) diventa:

f = fo (1 - v²/2c²)

La variazione da combinare con la (3) è quindi:

- fo v²/2c²          …. (5)

La variazione totale di frequenza è quindi data dalla somma di (3) e di (5):

Δf = fo (gH/c² - v²/2c²)

Ciò vuol dire che se dt è il tempo (numeri di giri in un certo periodo di tempo) misurato da un orologio fermo, quello dell’orologio in modo è dato da:

dt (1 + (gH/c² - v²/2c²))

Ovviamente, la quantità “in eccesso” va integrata per tutto il periodo del moto. Il suddetto integrale deve essere un massimo:

1/c²∫ (gH - v²) dt = massimo

Prima di procedere ricordiamo che gH non è altro che il potenziale gravitazionale.

Adesso, facciamo un giochino divertente. Moltiplichiamo l’integrale per la quantità -mc² sicuramente negativa. Il che vuol dire che l’integrale da massimo diventa un minimo, ossia l’oggetto si muove in modo che la nuova quantità sia un minimo. Proviamo a riscriverla …

∫ (- gHm + mv²/2) dt   = minimo.

Ma, attenzione: gHm è l’energia potenziale, mentre 1/2 mv² è quella cinetica, il che porta alle conclusioni descritte dalla legge di Newton (credetemi sulla parola!). La legge di Newton viene confermata dalla RG ipotizzando velocità di spostamento molto piccole. Einstein era proprio un mago!!

Riuscire a ritrovare la legge di Newton, stravolgendo completamente l’essenza del problema è un risultato che non poteva che sconcertare prima e strabiliare dopo.

Per sintetizzare la nuova visione einsteniana possiamo dire che Einstein cambia la gravità newtoniana in termini di geometria dello spaziotempo. La curvatura è ciò che comanda i movimenti degli oggetti e la massa è ciò che causa la curvatura. Più facile di così…

Le particelle seguono una ben definita legge muovendosi nello spaziotempo, ossia seguono le traiettorie (linee ferroviarie)  in cui gli orologi segnano il massimo tempo. Massimo tempo prende il posto di minima distanza nella visione newtoniana. In altre parole, il tempo proprio di una traiettoria deve sempre essere quello massimo.

La materia dice allo spaziotempo come incurvarsi, e lo spazio curvo dice alla materia come muoversi (J. Wheeler)

Conclusioni

Le leggi che governano la relatività generale sono, in pratica, due:

(1) Il cambiamento della geometria dello spaziotempo a causa della presenza di una massa. Esso  viene espresso come “eccesso” di raggio di curvatura, in funzione della massa, all’interno di una certa sfera (non confondiamo sfera con curvatura dello spazio; la sfera indica solo il volume in cui deve essere contenuta la massa), come ricavato precedentemente.

(2) Il moto di un corpo è soggetto solo alla gravitazione, ossia alla curvatura imposta dalla massa.

Queste due leggi sono molto simili a quelle su cui si basa la meccanica classica. La prima è la legge di Newton sull’inverso della distanza; la seconda è la descrizione del moto conseguente. La relatività generale potrebbe essere scritta semplicemente come:

R = GE

Dove R è una costruzione matematica composta da 16 numeri in una matrice o tensore che descrive la distorsione dello spaziotempo. Essa sarebbe in pratica ciò che Newton indica con F. G è la costante di gravitazione (quella resiste sempre). E è un altro numero molto complicato, descritto anch’esso da un tensore, che rappresenta l’energia dell’oggetto. In parole molto semplici il prodotto delle masse di Newton, ma con qualcosa in più…

Potremmo scriverla in modo molto più esteso, ma possiamo limitarci a questo:

R_μυ - ½ Rg_μυ = 8 πG T_μυ/c⁴

Dove R_μυ è il tensore di Ricci, R la curvatura scalare, g_μυ il tensore metrico, T_μυ il tensore energia-impulso. Non illudiamoci, però, essa sembra una sola equazione, ma in realtà dà luogo a molte equazioni dipendenti dalle componenti dei tensori. Tanto per dare una vaga idea di ciò che è contenuto in questo capolavoro, possiamo dire che bisogna tenere conto di tre dimensioni spaziali e di una temporale, che vengono evidenziate dalle lettere μ e υ che compaiono nei tensori. Il tutto può combinarsi in vari modi. Tant’è che le soluzioni dell’equazione, per le varie situazioni, non sono certo cose che possono farsi velocemente con carta e matita.

Non per niente, esse sono arrivate durante gli anni successivi e ancora ce ne sono probabilmente di segrete… E’ inutile proseguire se no si rischia di creare ancora più confusione.

La formula precedente è quella a cui giunse Einstein dopo aver eliminato dal primo membro una costante Λ, con segno negativo, detta costante cosmologica. Einstein l’aveva introdotta per mantenere un Universo statico (l’errore più grande della sua vita, ebbe a dire). Quando Hubble scoprì che l’Universo era in espansione, quella costante venne tolta. Tuttavia, cambiandone il segno essa riuscirebbe a spiegare un’eventuale accelerazione dell’Universo e, di conseguenza, l’energia oscura… Tuttavia, quella costante potrebbe in qualche modo essere legata al vuoto-non vuoto e poter tornare utilissima. Chissà… Einstein era un genio anche quando sbagliava…

Appendice: La curvatura è veramente così difficile da descrivere?

Voglio lasciare da parte questa breve chiacchierata sulla curvatura, non perché sia difficile (anzi…), ma perché serve solo a riflettere sulla problematica mostruosamente complessa. Nella meccanica newtoniana siamo abituati a relazioni tra spazio e tempo (attenzione spazio e tempo e non spaziotempo), così come siamo abituati a descrizioni puramente geometriche nello spazio. Il vero problema di Einstein è che niente si può fare in una qualsiasi della quattro dimensioni senza che le altre ne siano influenzate. Ne segue, in parole molto povere, che, qualsiasi tipo di curvatura affrontiamo, siamo obbligati a considerarla sempre nello spaziotempo.Insomma, un problema di matematica VERAMENTE superiore…

Noi vogliamo solo illustrare qualche curvatura di ordinaria amministrazione, che affrontiamo normalmente, e che dà un contributo sostanziale nella parte di formula che è legata alla geometria spaziotemporale (quella di sinistra, ossia quella che descrive come ci si può muovere).

Consideriamo la Terra e scaviamo il famoso tunnel che passi da parte a parte. L’avevamo trattato ampiamente QUI. .

Il moto delle sfere lasciate libere in quel foro è influenzato solo dalla gravità (anche se definita in modo abbastanza peculiare). Tuttavia, pur rimanendo nell’ottica newtoniana è facile assistere a un andamento curvilineo di spazio verso tempo. Lo illustra perfettamente la Fig. 25, dove quattro palline sono lasciate libere (due vicino al boro esterno e due all’interno del tunnel). Come sappiamo esse oscillano impiegando lo stesso tempo a tornare al punto di partenza e quindi è facile vedere l’andamento dello spostamento rispetto al tempo. Nella prima parte le curve tendono a unirsi (curvatura positiva), nella seconda parte si allontanano (curvatura negativa). Situazioni analoghe capitano al di fuori della Terra.

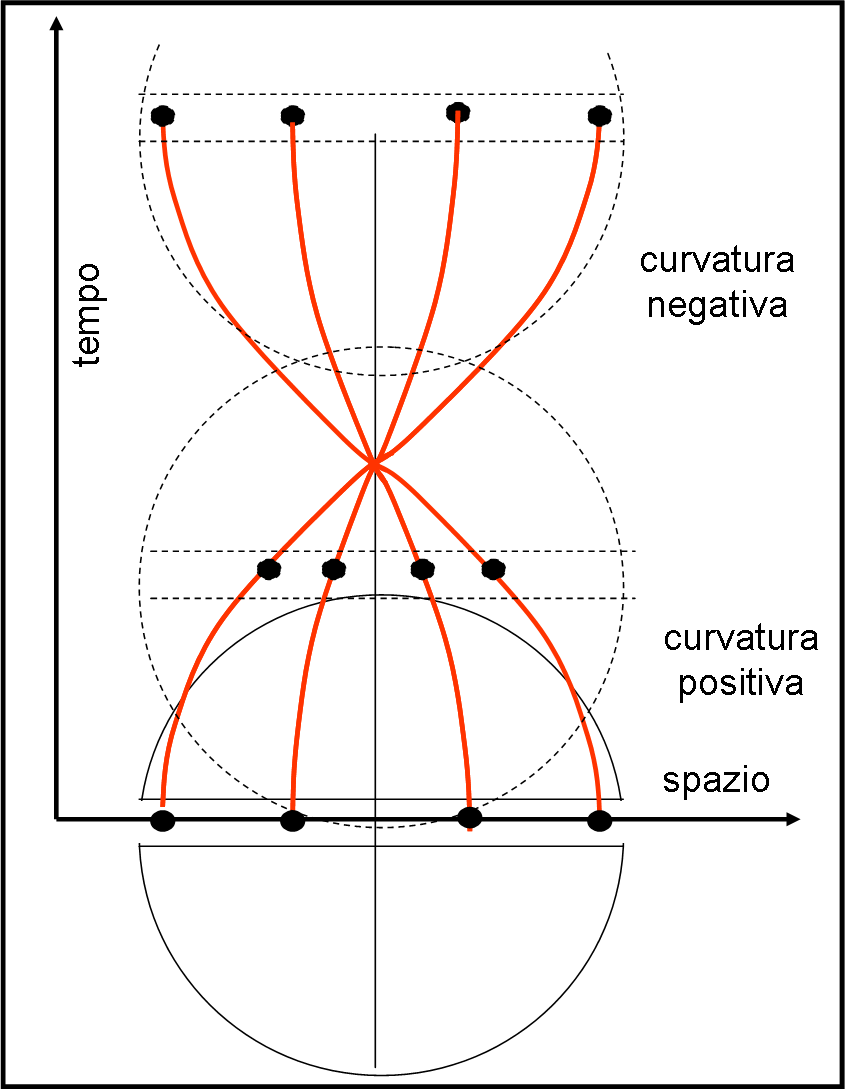
Consideriamo tre particelle che siano in preda alla gravità e che siano posizionate lungo la stessa direzione rispetto al centro di massa. Esse sono in caduta libera. Tuttavia, quella più lontana subisce una gravità minore di quella più vicina alla Terra, ossia la sua velocità è inferiore rispetto a quella più avanzata. Ne segue che il diagramma spazio in funzione del tempo descrive delle curve, per ogni pallina, che si discostano sempre più. Siamo di fronte a una curvatura negativa (Fig. 26).

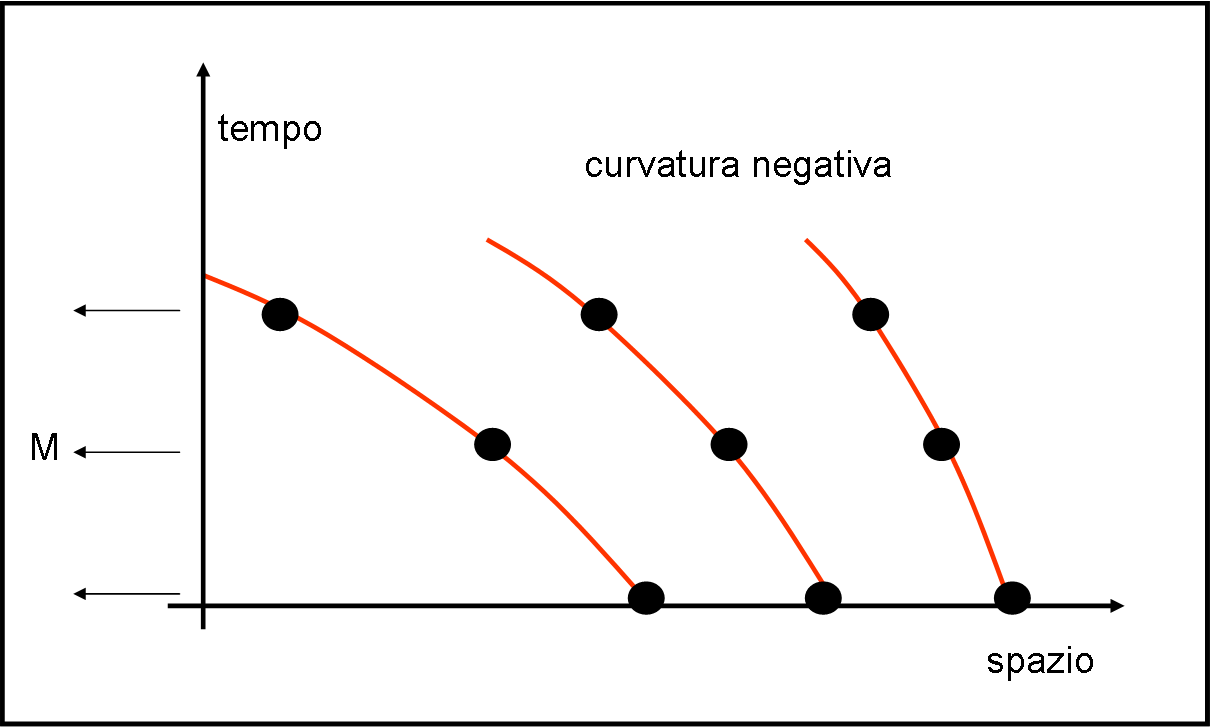
Consideriamo, adesso, in Fig. 27, tre particelle che stiano tutte alla stessa distanza dalla Terra (qualsiasi piano andrebbe bene).

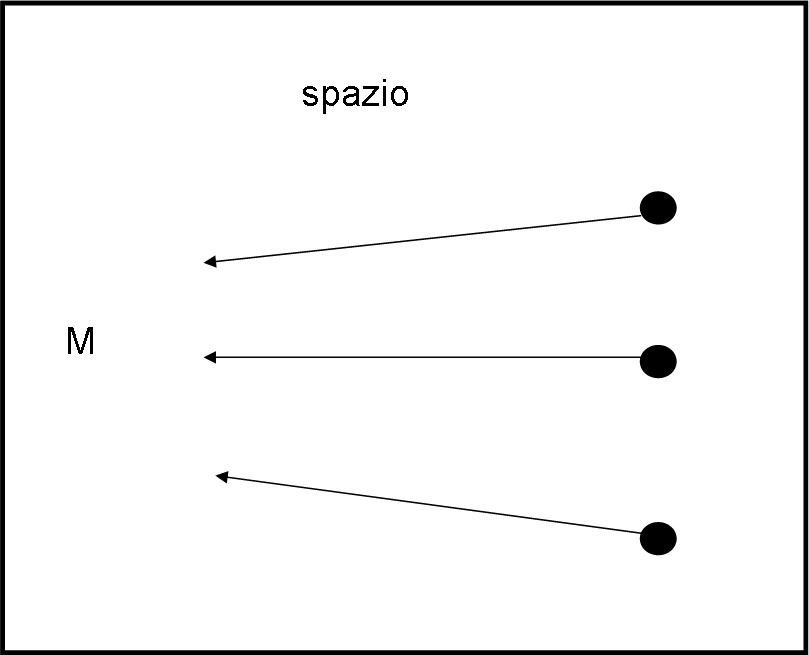
Esse hanno la stessa velocità in ogni momento, ma questa aumenta continuamente. Inoltre, la traiettoria di ognuna di esse è diretta verso il centro di massa e, quindi, si avvicinano. Se rappresentiamo le traiettorie rispetto al tempo, abbiamo le curve di Fig. 28, dove siamo di fronte a una curvatura positiva.

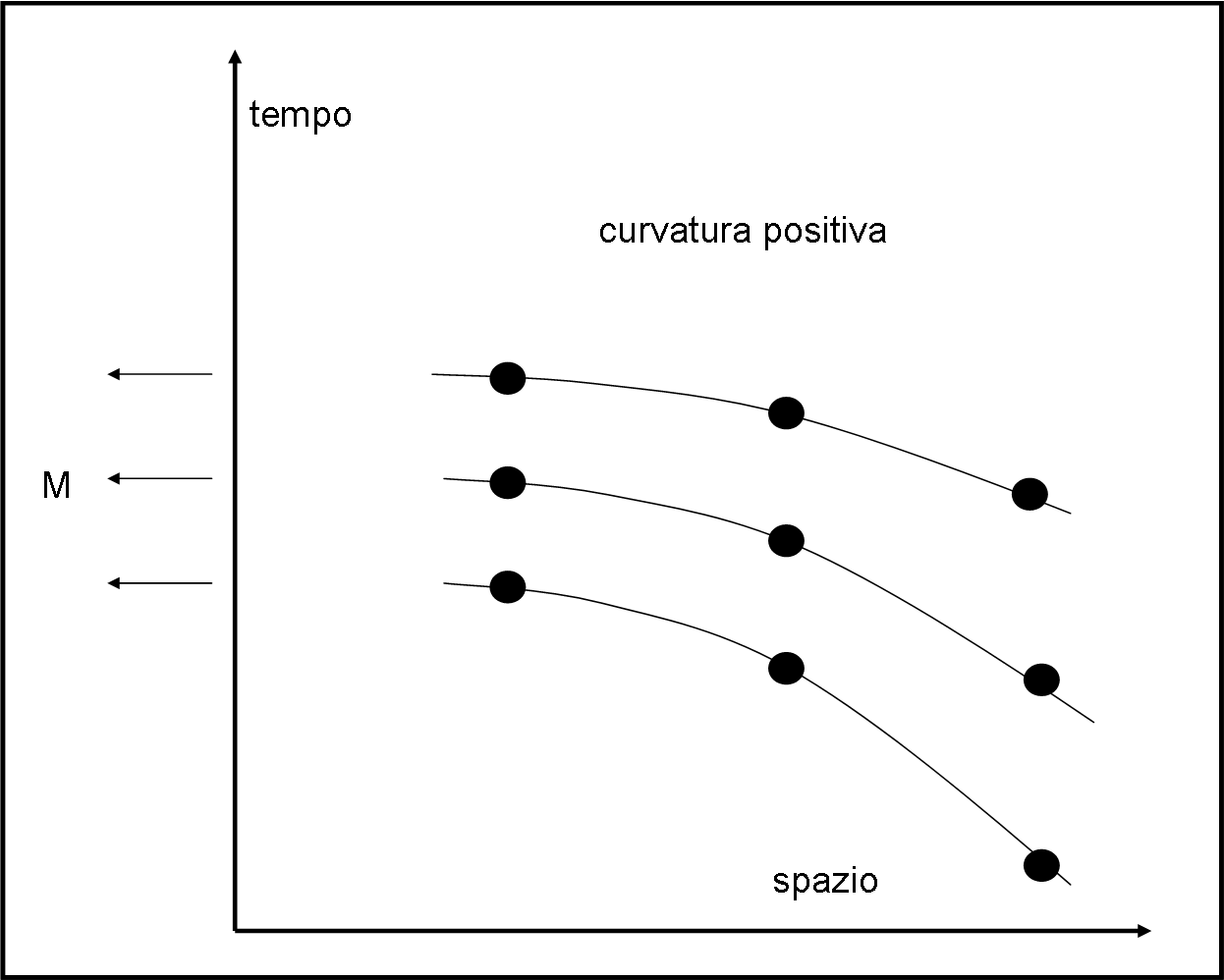
Per riassumere in modo banale la questione, pensiamo a uno spazio bidimensionale che giace sul piano orizzontale e due piani perpendicolari di spazio- tempo. Newton potrebbe descrivere i moti nei piani perpendicolari, mentre una semplice geometria euclidea descrivere le traiettorie sul piano orizzontale. Einstein invece deve descrivere qualsiasi traiettoria nello spaziotempo che non è certamente una media brutale delle varie curvature… Non è difficile comprendere quale ostacolo si sia trovato di fronte…

Non siamo di fronte a un "uomo che parlava ai cavalli", ma a qualcosa di simile (dato che anche i cavalli sono Universo): Einstein, l'uomo che parlava al Cosmo!

 

QUI parliamo dei TENSORI, la colonna (matematica) portante della Relatività

 

L'ANGOLO DEI CURIUSS-ONI

Dieci curiosità più o meno note sulla teoria della Relatività Generale, raccontate da Curiuss al "curiosissimo" micione Gualtiero: a partire dalla storia dell'imbianchino che l'avrebbe ispirata, fino all'eclissi di Sole del 1919 che servì a dimostrarla, passando dai giornali francesi che non ne diedero notizia perché... per non parlare poi della Prima Guerra Mondiale che la salvò!

E anche fusa di gatto Gualtiero che si trasformano in crocchette: questo e altro (tra cui qualcosa di serio) ci spiega Curiuss in "5 cose sconvolgenti contenute in E=mc²"

Finalmente anche Gatto Gualtiero si è deciso a miagolarci del concetto di Relatività da Giordano Bruno (ebbene sì, proprio lui è stato il primo) fino ad Albert Einstein, passando per Galileo e Newton! Ascoltiamolo in miagoloso silenzio...

Dopo una bella scorpacciata di Relatività, poteva Curiuss dimenticarsi di raccontarci i retroscena della sua prima verifica sperimentale? No, per nostra fortuna, non poteva!