Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Abbiamo già parlato di aberrazione della luce. Un argomento che porta a  conclusioni spesso contro intuitive. Tuttavia, è un fenomeno astronomico molto importante perché riesce a trascinare qualsiasi persona all’interno della relatività ristretta. A tal punto che si può simulare, con qualche difficoltà in più, un viaggio nello spazio a velocità altissime e dimostrare come tutto appaia in modo estremamente “stravagante”. Ho reputato, quindi, doveroso iniziare trattando l’aberrazione in modo ultra semplificato, in modo da eliminare certe difficoltà di comprensione di base (che spesso non sono adeguatamente spiegate) e permettere a tutti di prendere posto sulla nostra astronave.

L’idea di riprendere in mano l’aberrazione  e ciò che si vedrebbe viaggiando a velocità comparabili a quelle della luce mi è stata data contemporaneamente da Daniela e da Gianluigi, un nuovo amico ingegnere che lavora nel Qatar… (beato lui, con il freddo che fa da noi!). Daniela si è ricordata di un articolo in cui si descriveva come fosse stato scoperto un esopianeta attraverso l’aberrazione relativistica (chiamato appunto pianeta di Einstein).

In quella occasione si andava un po’ più a fondo. Ciò mi ha ricordato che avevo trattato il fenomeno descrivendo cosa vedrebbe un astronauta che viaggiasse a velocità relativistiche, attraverso articoli non proprio banali. Gianluigi, invece,  mi ha mandato una sua elaborata simulazione degli effetti relativistici e del panorama visibile dall’astronave. Non poteva essere un caso e, allora, mi sono deciso a riprendere in mano la faccenda iniziando proprio da zero, cercando di portare nel nostro viaggio tra le stelle anche chi è sempre restato un po’ al bordo della Relatività Ristretta. Pochi fenomeni riescono a far passare da una visione galileiana a una einsteinana con pochissima difficoltà come questo…

Un giorno di pioggia

E’ il metodo più usato per introdurre l’aberrazione astronomica, quella che ci interessa in particolare. Noi la trattiamo in modo super elementare in modo da non lasciare alcun dubbio sull’effetto risultante.

Ci facciamo aiutare dalla Fig. 1.

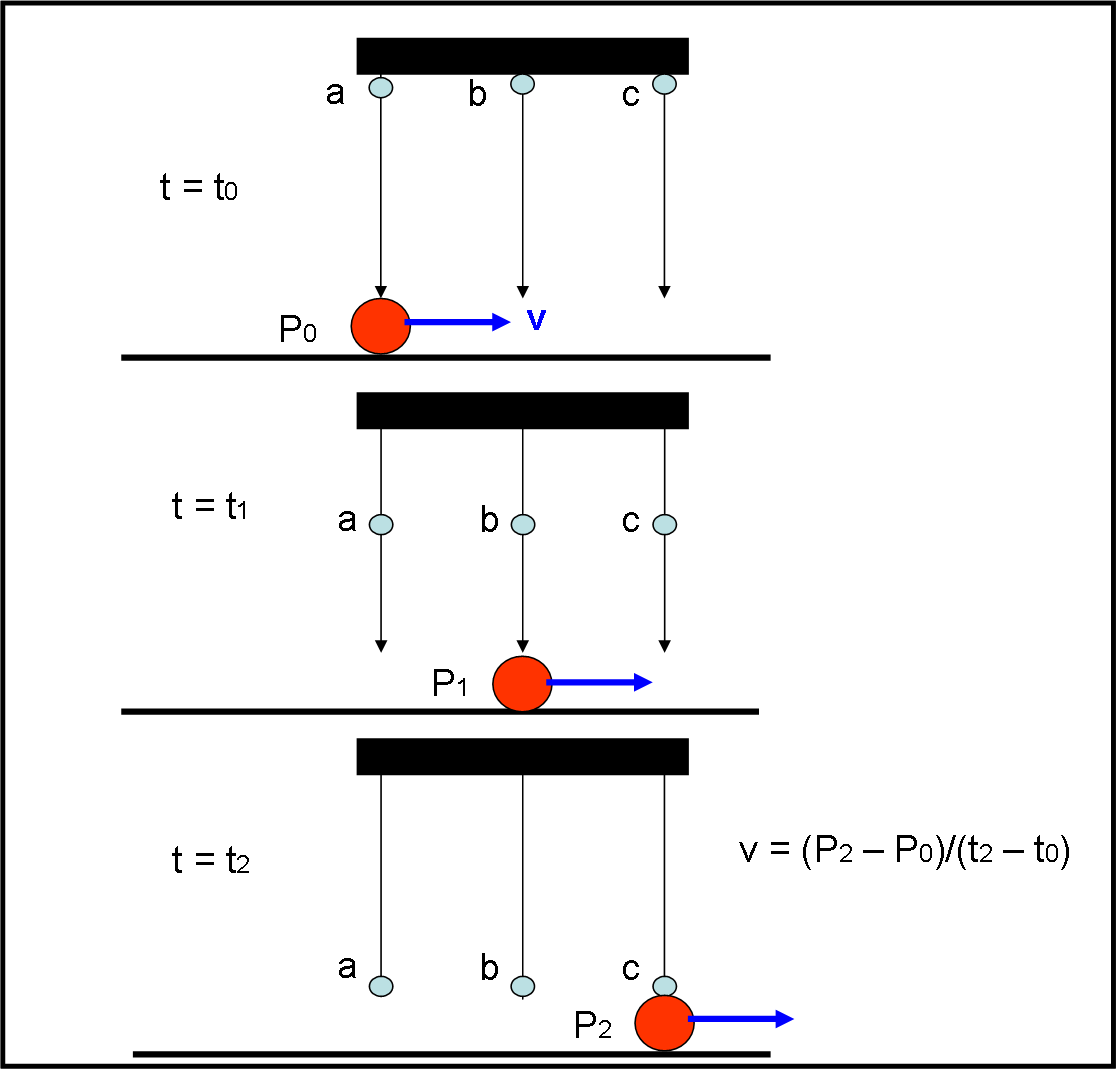
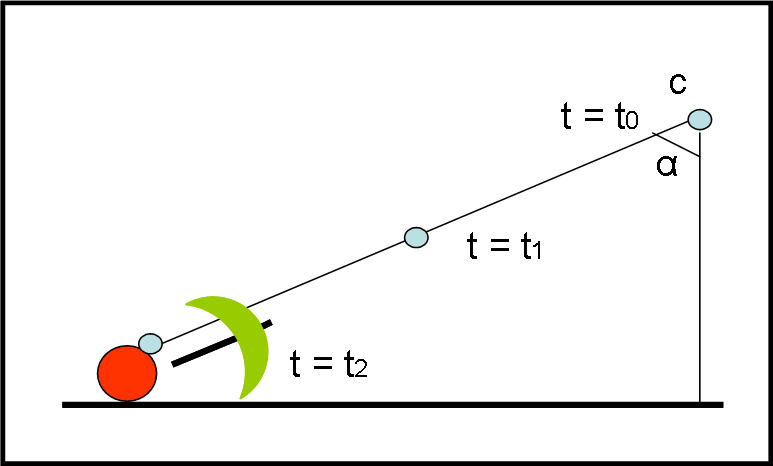
In alto c’è una nube minacciosa, da cui cadono tre gocce di pioggia (a, b e c) allo stesso istante (t = t₀). Esse si dirigono verso il basso con la stessa velocità e quindi toccano il suolo allo stesso istante t = t₂ (figura in basso). All’istante t₁ si trovano, perciò, a una certa altezza (figura mediana). Immaginiamo che ci sia una persona P (forse un papallicolo, vista la sua forma…) sulla strada. Purtroppo, non può fare molto e deve bagnarsi. Tuttavia, cerca di muoversi in fretta per cercare un riparo. La sua velocità (costante) è data da v che è, ovviamente, uguale allo spazio percorso in un certo periodo di tempo. Essa è quindi data dalla differenza delle posizioni P2 e P0 divisa la differenza tra il tempo t2 e il tempo t0. Comunque, per adesso, non ci interessa molto se non per il fatto che P si muove in modo costante.

Un osservatore, al caldo e all’asciutto, vede tutta la scena dalla finestra. Cosa può raccontare? In alto la persona P sta esattamente in P0 sotto la goccia a, ma, dato che si muove, quando essa arriva al suolo, lui non è più in quella posizione. La stessa cosa succede per la goccia b. Quando P si trova n P1 ce l’ha sopra la testa, ma ancora troppo distante. La goccia pericolosa è la c. Essa aspetta al varco la nostra persona. Quando arriva in P2, la goccia c lo colpisce sulla nuca e lo bagna.

L’osservatore esterno conclude, con grande sicurezza, che la pioggia cade esattamente in verticale e che, dato che la persona si muove verso destra, viene colpita dalla terza goccia. Tutto perfetto…

La faccenda, però, cambia notevolmente se cambiamo sistema di riferimento. Il fenomeno fisico deve essere lo stesso (P deve essere colpito in P2 dalla goccia c). Tuttavia, la descrizione del fenomeno visto da P, che si considera fermo, è un po’ diversa.

Lui vede, al tempo t = t₀, la goccia a sopra di lui, ma non si preoccupa più di tanto, in quanto tutta la nube nera si sta spostando verso sinistra con velocità -v. Ricordiamo che lui si considera fermo e quindi sono la nuvola e le gocce che si muovono verso sinistra. Non si preoccupa nemmeno della goccia b, in quanto quando arriva sopra la sua testa è ancora troppo in alto. Fin dall’inizio, il nostro P ha puntato la goccia c. Essa sembra proprio spostarsi verso sinistra in modo da colpirlo. E così capita. Il fenomeno si è verificato anche nel sistema di riferimento di P. Ma lui cos’ha visto esattamente? Presto detto: la goccia c si è mossa in diagonale e l’ha colpito in pieno.

La Fig. 2 sintetizza la visione di P.

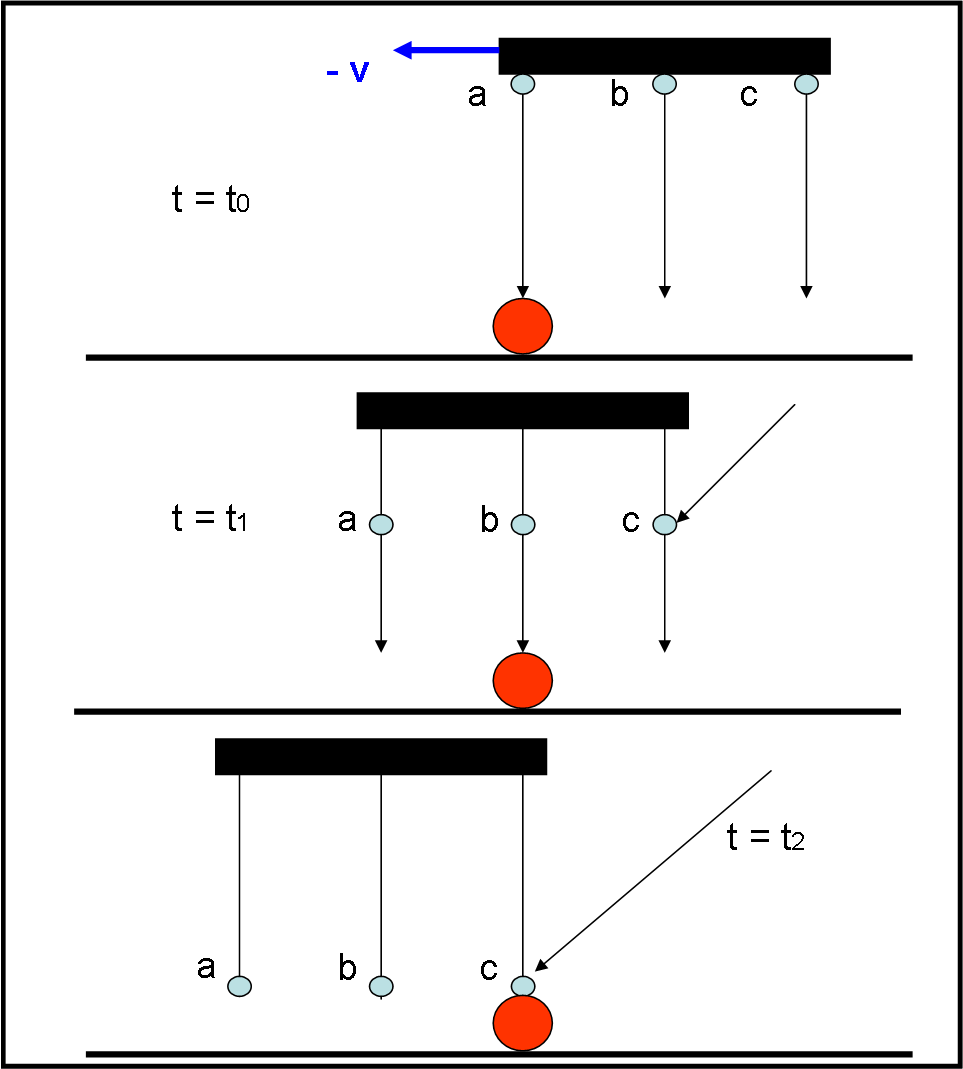
La goccia c si è diretta verso P seguendo una traiettoria rettilinea che forma un angolo α rispetto alla verticale. Se P avesse un ombrello, come dovrebbe sistemarlo per proteggersi dalla goccia c (l’unica che può colpirlo)? Nel modo rappresentato in Fig. 3, ossia diretto verso la traiettoria diagonale!

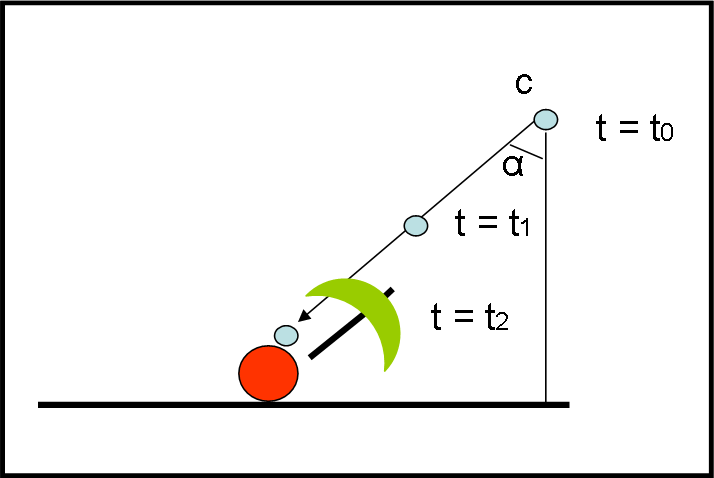
Ecco perché chi si muove mentre piove punta l’ombrello inclinandolo nel verso del moto. E più va veloce e più l’ombrello deve inclinarsi (a pari velocità di caduta della pioggia), come mostrato in Fig. 4 e 5(abbiamo indicato solo le gocce a e c). Non c’entra niente, quindi, il vento… ma è solo una questione di composizione vettoriale di direzioni di velocità (quella di caduta e quella di fuga della persona P – le nozioni sui vettori le trovate all’inizio di questo articolo)

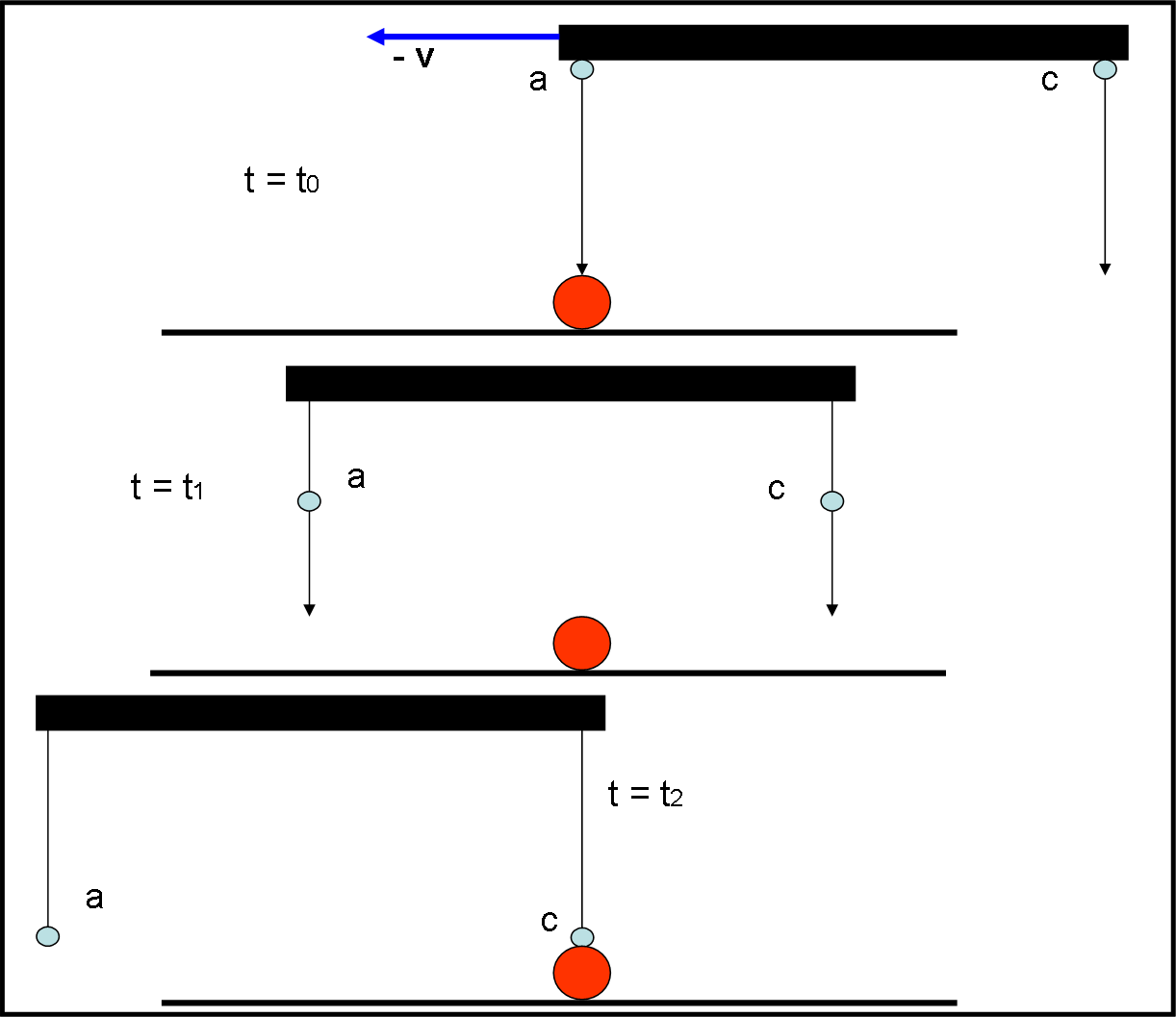
Non è difficile passare a qualcosa di più astronomico. Immaginiamo che, adesso, le gocce di pioggia siano dei fotoni inviati da una stella S (Fig. 6). Il fatto che P si muova a passo svelto conta ben poco. Ma è invece importante il fatto che la Terra si sposti lungo la sua orbita con una velocità v ben maggiore (circa 30km/sec).

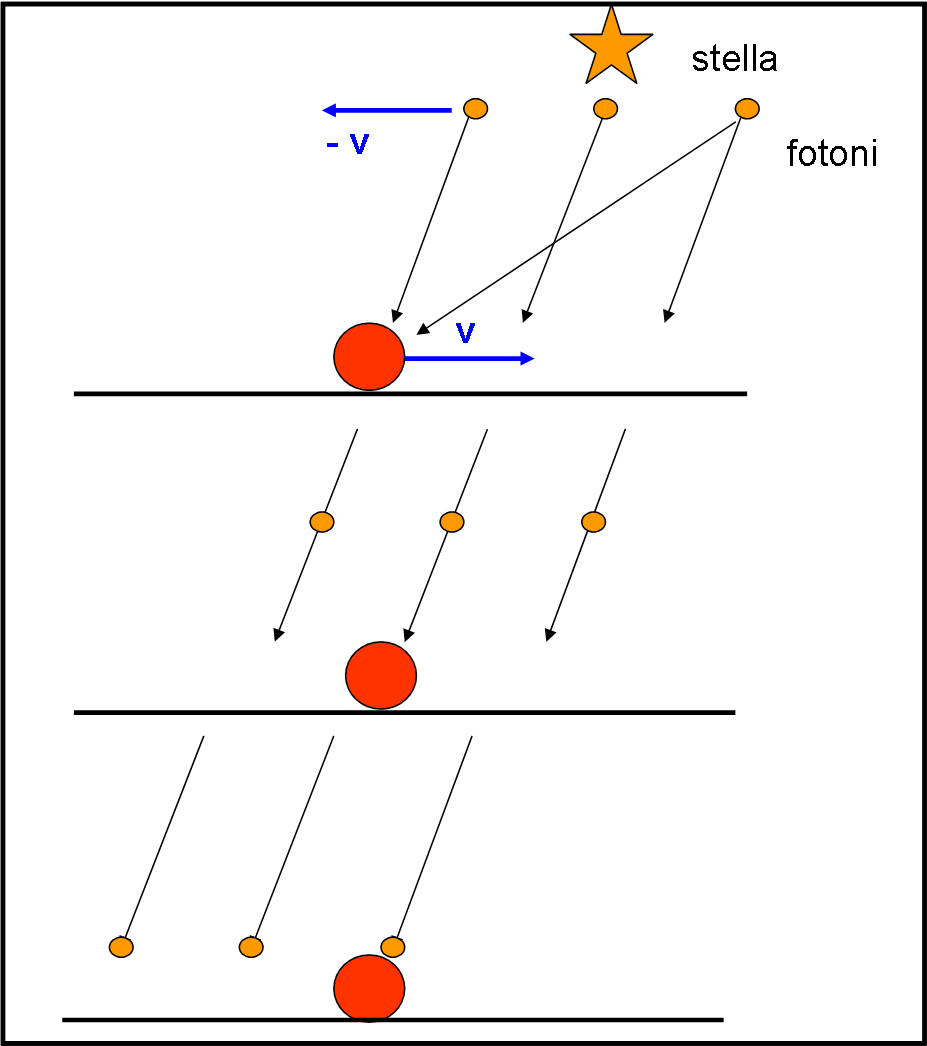
Ne deriva che per essere colpito da un fotone inviato dalla stella bisogna puntare la posizione del terzo fotone. Ne consegue, come prima, che il telescopio va inclinato di un certo angolo rispetto alla direzione vera della stella (quella che determinerebbe un osservatore centrato nel Sole, considerato fisso), come mostrato in Fig. 7. La stella sembra trovarsi in una posizione sempre diversa, che dipende dalla sua posizione nel cielo rispetto al moto orbitale della Terra.

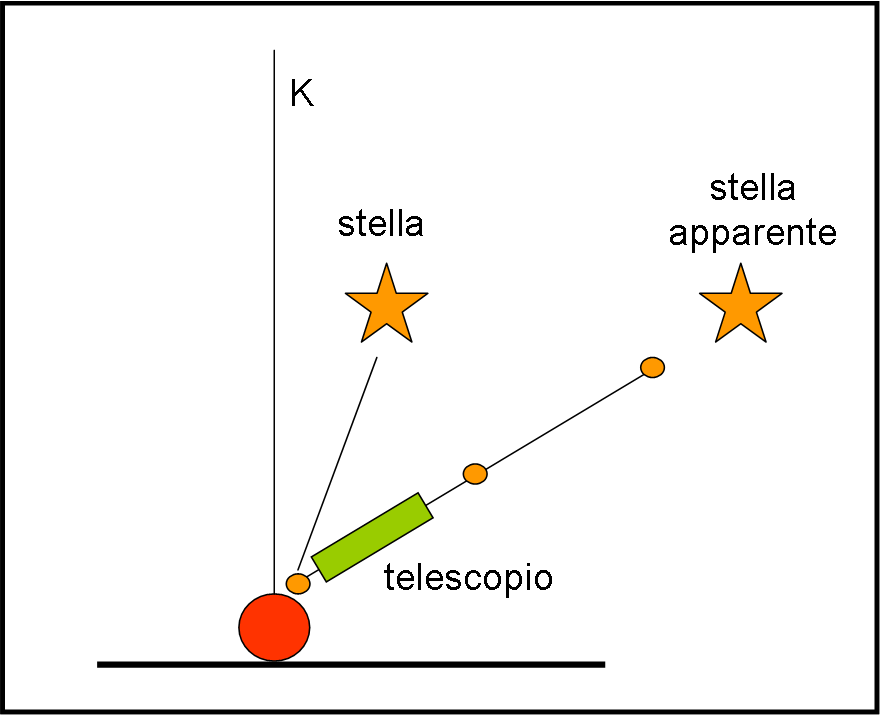
Ovviamente, noi non riusciamo a vedere il singolo fotone quando sta per arrivare, così come non riusciamo a vedere la goccia di pioggia prima che ci colpisca. Comunque, esisterà sempre una goccia o un fotone che si trovano nella posizione giusta al momento giusto. Troveremmo, così, che la posizione della stella rispetto, ad esempio, alla direzione del polo dell’eclittica K (cos’è l’eclittica lo abbiamo spiegato QUI), sarà diversa da quella che ha in un sistema eliocentrico. In realtà, il moto della Terra avviene lungo un’ellisse e quindi la posizione apparente della stella descrive anch’essa un’ellisse seguendo il moto della Terra. Questa ellisse è più grande di quella parallattica e dipende solo dalla posizione delle stelle e non dalla loro distanza.

Scegliamo un fotone fin dall’inizio

Alle stesse conclusioni arriviamo se decidiamo di catturare proprio un fotone, uno solo e non un altro! Partiamo quindi dal momento in cui il fotone tocca il centro dell’obiettivo O del nostro telescopio (a lente, per ipotesi, oppure questo oppure uno dei quali abbiamo parlato QUI). Per semplicità immaginiamo che il fotone arrivi proprio dallo zenit (la vera posizione della stella), ossia viaggi perpendicolarmente rispetto al suolo (Fig. 8).

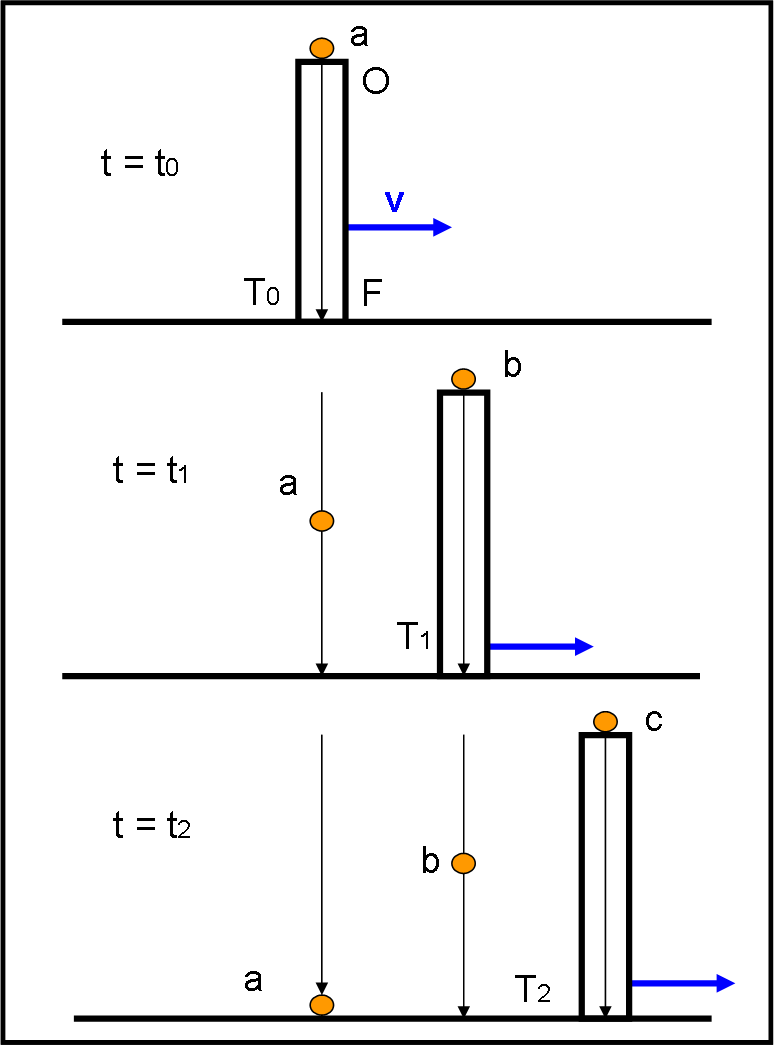
Sembrerebbe ovvio mantenere il telescopio nella stessa direzione perpendicolare… Niente di più sbagliato! Se lo facessimo il fotone finirebbe contro il tubo del telescopio e/o uscirebbe quasi subito da lui se non ci fosse il tubo (come capita per i grandi telescopi a specchio). Perché? Per il semplice fatto che il telescopio si muove insieme alla Terra. Giunto nella posizione mediana catturerebbe un altro fotone, ma non sarebbe quello di prima e inoltre uscirebbe subito anche lui dal tubo e non arriverebbe mai nel fuoco F.

Vediamo la situazione nella Fig. 9, dove ci mettiamo nel sistema di riferimento del telescopio.

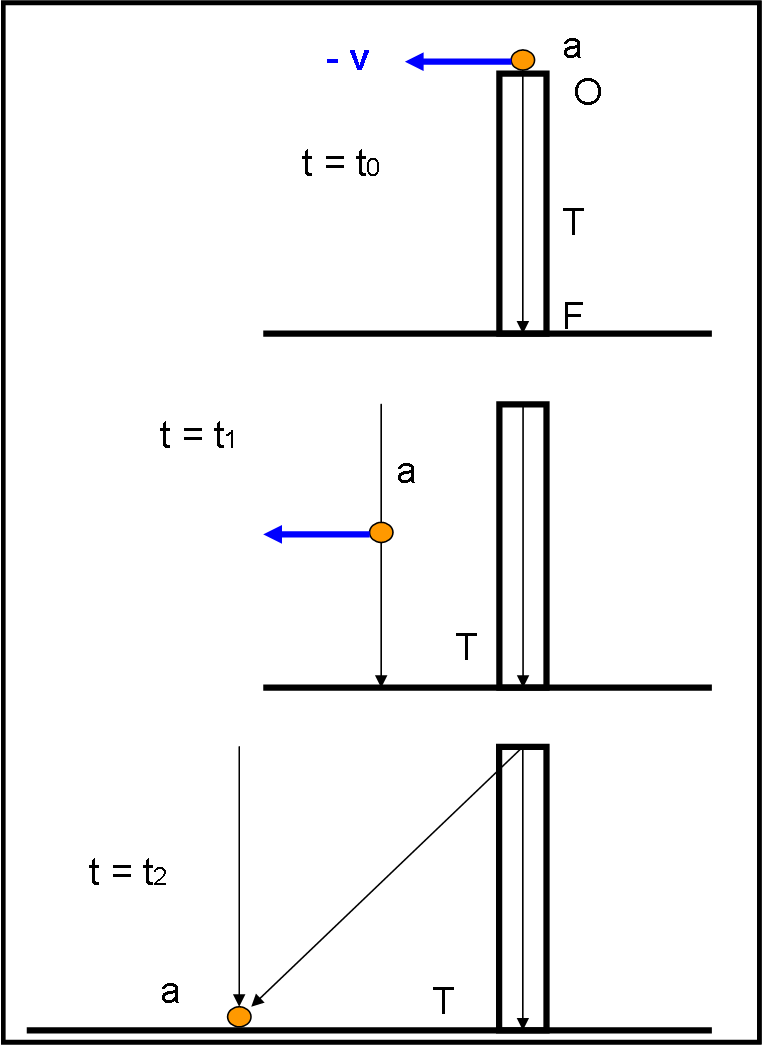
Il fotone “sembra” viaggiare in diagonale verso sinistra. La direzione del fotone è proprio quella che ci serve per puntare esattamente la stella. Dobbiamo piegare il telescopio come illustrato in Fig. 10 . Il fotone continua a cadere perpendicolarmente, ma il telescopio che si muove lo accoglie fino a portarlo al fuoco F.

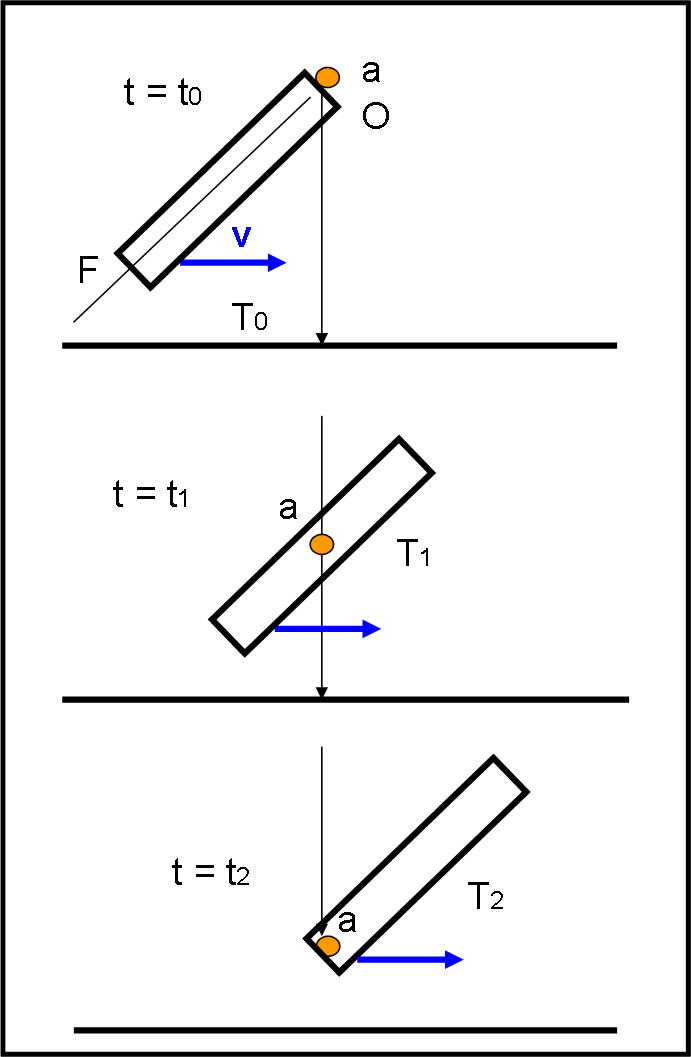
La Fig. 11 mostra cosa capita nel sistema di riferimento del telescopio, del tutto simile a quanto avevamo trovato nella Fig. 7.

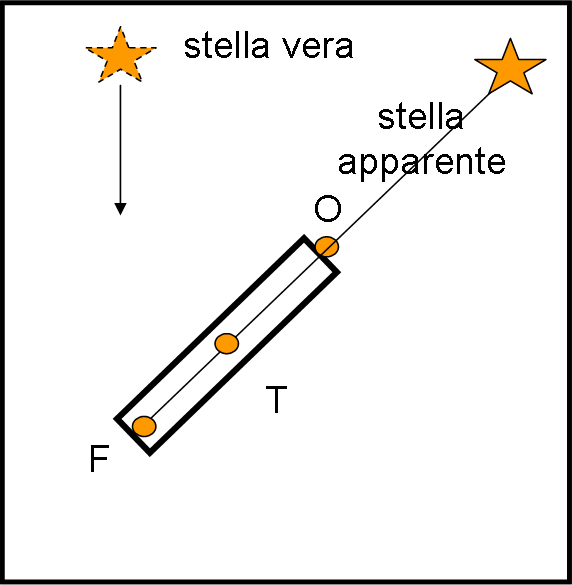
L’argomento esplode letteralmente. Innanzitutto ha permesso di calcolare la velocità della luce. Inoltre si intuisce facilmente che la combinazione vettoriale di velocità della luce e di movimento di P può dare solo una differente direzione, ma non certo una differente velocità (Einstein si arrabbierebbe non poco, visto che la velocità della luce non si può superare!). Ne consegue un legame strettissimo con la relatività ristretta (la nostra astronave sta riscaldando i motori). In altre parole, l’aberrazione è un fenomeno relativistico che può essere risolto anche in modo classico (basta solo evitare di sommare esplicitamente la velocità della luce con la velocità della Terra o di chi per lei.

Insomma, ne avremo per tutti i gusti, non ultimo l’effetto di questo fenomeno sulle coordinate geocentriche delle stelle. La prossima volta inseriremo qualche formuletta veramente banale...per poi arrivare alla formula data dallo stesso Einstein nel 1905. Dovremo stare molto attenti ai segni (sul web si fa un po' confusione), dato che nel caso dell'aberrazione annua  è la Terra che si muove, mentre, in  altre applicazioni relativistiche, si muove la sorgente luminosa. Ancora una volta, occhio ai sistemi di riferimento.

Prima di cominciare a scendere nei dettagli, però, digeriamo bene il concetto di base, altrimenti i dubbi diventeranno ostacoli invalicabili nei prossimi articoli.