Categorie: Relatività
Tags: accelerazione movimento paradosso dei gemelli relatività generale relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:79
Il paradosso dei gemelli non esiste realmente (per chi ha capito la relatività) ****
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
Questo articolo ha quattro asterischi non tanto per i concetti che espone, quanto perché necessita di una buona conoscenza sia della relatività speciale sia di quella generale. Inoltre, affronta ancora una volta il paradosso dei gemelli nella forma da molti usata come la più ovvia, ma che lo è solo apparentemente. Si sente dire: “Basta tener conto della RG è tutto diventa banale”. Sì, ma come e perché? Più che una spiegazione, l’articolo vuole essere una possibile fonte di discussione, dato che l’interpretazione che viene data è abbastanza personale e non da tutti accettata.
Abbiamo affrontato il paradosso dei gemelli in vari modi e tutti corretti, utilizzando solo la RR (relatività ristretta). In particolare, il diagramma di Minkowski ce l’ha mostrato chiaramente: il massimo tempo proprio indica chiaramente la traiettoria seguita nello spaziotempo a velocità costante (o da fermo). Se la velocità non è costante, dato che cambia direzione, il tempo proprio diminuisce. Sembrerebbe quasi di poter concludere che il tempo passa più lentamente per colui che si muove REALMENTE (un’assurdità nella RR dato che sembra pretendere un sistema assoluto di riferimento).
Frase, questa, che fa rizzare capelli in testa, lavorando in RR. Essa ci dice che è impossibile stabilire chi si muove e chi sta fermo. Entrambi i gemelli, nel proprio sistema di riferimento, vedono rallentare l’orologio di chi si muove. Per risolvere la questione bisogna assolutamente modificare il sistema di riferimento. Insomma sembra quasi necessario restare nella RR per risolvere il paradosso, malgrado si dica sovente che tutto si risolverebbe più facilmente nella RG (relatività generale) in quanto l’astronave accelera, decelera, accelera di nuovo e poi decelera per tornare a casa.
Permettetemi di dire che sono “frasi fatte”, che, in realtà non dimostrano un bel niente. A meno di non interpretarle correttamente (sempre che ci si riesca).
La faccenda è più complicata del previsto e in questo ci viene incontro la parte finale della nostra trattazione della RG, quando cercavamo di far MUOVERE una pallina, immersa in un campo di gravità, e ottenere il massimo tempo proprio. Avevamo visto che si riusciva a ottenere il risultato voluto lanciando in alto la pallina. Essa subiva un’accelerazione, una decelerazione, una nuova accelerazione e infine l’urto finale sulla terra. Insomma, era necessario un gioco combinato di RR e RG. Vi era, in fondo, anche una decelerazione finale, istantanea, che trasformava una certa velocità in velocità nulla in un tempo uguale a zero.
In tutto ciò torna ad avere valore chi si muove e chi non si muove. Ciò che era assurdo nella RR non lo é più nella RG. Nella RG, noi che siamo fermi sappiamo benissimo chi è che si muove, ma lo sa anche chi si muove (cosa che nella RR non era vero).
Come fa a saperlo? Facilissimo: chi subisce gli effetti di un’accelerazione o decelerazione sa benissimo di non essere in un sistema inerziale e quindi sa benissimo di muoversi! Abbiamo detto una banalità? Neanche per sogno… ancora adesso vi sono diatribe e discussioni a proposito. Il paradosso dei gemelli, utilizzando la RG, solleva problemi ben più grandi di quando viene trattato solo con la RR. Fatemelo dire con altre parole…
Chi è convinto di stare fermo non ha nessuna prova di muoversi e può continuare a sentirsi nella RR. Lui vede partire l’astronave ed è convinto che sia lei che si sta muovendo. Se rimaniamo nella RR, l’astronave può permettersi di dire lo stesso e per lei è chi sta fermo che si muove con velocità uguale e contraria. Vi è una perfetta simmetria. Solo una rottura di questa simmetria (cambiamento il sistema) può fare ringiovanire il viaggiatore.
Se io viaggiassi a velocità costante, cosa farebbe la pallina che tengo in mano e lascio libera? starebbe ferma nella stessa identica posizione di prima. Se, invece, la vedessi cadere, capirei subito che sono in un campo accelerato, ad esempio un campo gravitazionale (principio di equivalenza).
Chi è accelerato sa anche che il suo orologio rallenta sempre di più a mano a mano che si avvicina alla massa. In qualche modo, è consapevole di viaggiare e di subire un rallentamento del suo orologio. In poche parole, e lo abbiamo anche detto nella trattazione della RG, bisogna tener presente sia la RR sia la RG: la loro combinazione ci regala la traiettoria percorsa da chi si muove realmente, ossia la geodetica.
La faccenda è quindi molto diversa. Riassumiamola ancora: chi sta fermo continua a sentirsi fermo e quindi non può che concludere che sia il viaggiatore a invecchiare di meno. Il paradosso di chi torna a terra, però, scompare, perché anche il viaggiatore sa di essersi mosso e quindi di essere rimasto più giovane. Lui ha sentito l’accelerazione e i suoi effetti (pallina che cade sul pavimento) e quindi non può che prevedere la sua effettiva giovinezza, dato che ha dovuto muoversi.
In altre parole ancora: il paradosso dei gemelli nella RG si risolve molto semplicemente ammettendo che entrambi i fratelli sanno chi si sta muovendo. Il primo perché lui non sente accelerazione, il secondo perché la sente. Il paradosso si scioglie. Ricordiamoci ancora che chi si muove impiega meno tempo a percorrere una certa traiettoria e quindi DEVE restare più giovane.
Nel web ne potete leggere di tutti i colori e leggere spiegazioni che sembrano illuminanti e che poi si mostrano completamente errate. Ve ne cito una che, a prima vista, sembrerebbe essere accurata e decisiva e … invece… (la potenza dei video…).
L’idea di base sembrerebbe giusta, soprattutto quando l’astronauta inverte la rotta. Si dice chiaramente che per tornare indietro il pilota deve accelerare. Facendo questo è come (principio di equivalenza) che si creasse un campo gravitazionale. Il viaggiatore è decisamente più vicino all’origine del campo fittizio di non quanto non lo sia la Terra e quindi la RG dice che il suo orologio DEVE girare molto più lentamente o -se preferite- quello della Terra deve girare molto più in fretta.
Durante il viaggio erano nella RR, ma nell’inversione sono ENTRAMBI nella RG. Anche il viaggiatore capisce che sta ringiovanendo rispetto al terrestre. Si dice anche giustamente che l’accelerazione alla partenza gioca di meno (in quel caso lui sarebbe più “in alto” rispetto a chi sta a Terra) e il suo orologio girerebbe più velocemente, ma in modo meno drastico di quanto succede nel pianeta alieno in cui la Terra è decisamente molto “più in alto”.
Sembrerebbe una buona spiegazione, anche perché alla fine si dice una sacra verità: entrambi sanno chi è che ha viaggiato.
In realtà (ma è una mia spiegazione che può anche essere confutata viste le polemiche ancora in corso), se ci poniamo in queste condizioni, vuol dire che anche chi sta sulla Terra si muove, ossia risente del fittizio campo di gravità che sente il viaggiatore. Se non si muovesse non dovrebbe assolutamente sentire niente e il suo orologio non dovrebbe accelerare. Accettare questa situazione vorrebbe, in pratica, dire che chi entra in un campo di gravità obbliga anche chi ne è del tutto estraneo a sentirne gli effetti. Ma questo non è vero! La gravità e i suoi effetti spaziotemporali sono sentiti solo da chi li sta subendo e non da chi ne sta fuori. E’ solo il cono di luce del viaggiatore che si piega. Quello esterno resta com’è… non c’è nessuna simmetria!
L’errore commesso in questa visione troppo semplicistica si può anche comprendere in altro modo.
Nel video si tratta solo l’accelerazione… Ma che dire della decelerazione? Essa produrrebbe qualcosa di uguale e contrario e il viaggiatore, mentre decelera arrivando nei pressi del pianeta alieno, risentirebbe della gravità che ha origine sulla Terra e che impone al suo orologio (molto più “in alto”) di girare molto più velocemente di quello terrestre. Insomma, secondo me, nascondendo una parte sotto la sabbia, si è reso comprensibile e convincente un qualcosa che non lo è affatto.
In particolare c’è una frase alla fine del video che mi lascia molto dubbioso: “Sia chi sta sulla Terra che chi viaggia é convinto di essere sempre stato fermo durante tutto il tempo”.
No, su questo io non sono d’accordo… Questa è, ovviamente, una mia visione della spiegazione, ma se qualcuno vede una interpretazione diversa me lo faccia sapere. Non sono affatto sicuro di essere nel giusto… come tanti altri ben più bravi di me…
Riflettiamo ancora un po’ sul paradosso. Se io fossi sicuro di stare fermo potrei concludere che chi si muove ha l’orologio più lento? Assolutamente SI. Prendiamo il muone, anzi due muoni: uno fermo e uno che arriva ad alta velocità sulla Terra. Normalmente si considera il muone che arriva a velocità costante e il discorso torna perfettamente, perché non ci si cura di cosa vede e sente il muone. Tuttavia, si può dire benissimo che il più giovane è quello che ha viaggiato! Noi siamo capaci di dirlo con certezza. E, in fondo, lo potrebbe dire anche il muone in viaggio, perché sa che sta subendo gli effetti della gravità! Si sente sicuramente diverso da suo fratello che non si è mosso. Il tempo in cui nascono i due muoni (quello terrestre e quello atmosferico) è un tempo terrestre (per esempio), ma appena l’alieno si muove, cambia il suo tempo e la simultaneità. E’ come se lui fosse ben più avanti del fratello a riposo. L’osservatore a terra, l’unico che valuta la situazione finale, direbbe che ha vissuto più a lungo, sia in RR che in RG.
L’esempio si può fare ancora meglio entrando in laboratorio. Costruisco due muoni. Uno lo lascio fermo, mentre l’altro lo faccio muovere velocemente lungo una circonferenza attorno al gemello, magari attraverso un campo magnetico costruito “ad hoc”. State pur certi che il muone fermo morirebbe prima del fratello in moto, ma non ci sarebbe nessun paradosso, dato che entrambi i muoni sanno benissimo chi dei due è in movimento! Quello fermo perché vede girare il fratello; quello in moto perché sente l’accelerazione e quindi non può nascondersi la verità.
Non prendete per oro colato tutto ciò che ho detto… A questi livelli “quasi filosofici” la discussione è ancora aperta e vede anche insulti reciproci. Un consiglio? Continuiamo a risolvere il paradosso con la sola RR… è molto meglio! Ma stiamo molto attenti a video che sembrano spiegare tutto attraverso immagini accattivanti…
QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli
79 commenti
La foto è tratta da un sito YouTube di divulgazione scientifica graficamente e didatticamente bravissimi,Eugene Khutoryansky è in Americano,ma per chi lo mastica vale la pena di visitarlo.
eppure questo filmato, secondo me, è sbagliato concettualmente...
Forza, cercatemi di convincere che sbaglio io da qualche parte... collaborazione!!!
Negli anni '50, fino ai primi anni '60, il professor Herbert Dingle (1890-1978) portò avanti una personale battaglia per contestare alcuni aspetti della relatività. Egli fu autore di un sillogismo che tenta di dimostrare come, nel caso del paradosso dei gemelli, il previsto rallentamento degli orologi in moto nasconda un'illogicità. Abbiamo infatti sostenuto che il moto è relativo, ma anche che il moto provoca un rallentamento degli orologi, e questa seconda affermazione sembrerebbe in grado di smentire la prima, consentendoci di individuare in maniera certa gli orologi in moto. In questo caso il termine "paradossale" starebbe a significare "impossibile".
Il sillogismo di Dingle recita così:
1 (Premessa maggiore) Secondo il postulato di relatività se due corpi (ad esempio due orologi identici) prima si separano poi si riuniscono non c'è alcun fenomeno osservabile che possa dimostrare in senso assoluto che uno si è mosso anziché l'altro.
2 (Premessa minore) Se dopo il riavvicinamento un orologio fosse ritardato di una quantità dipendente dal movimento relativo, e l'altro no, questo fenomeno mostrerebbe che il primo si è mosso e non il secondo.
3 (Conclusione) Pertanto, se il postulato di relatività è vero, gli orologi debbono essere egualmente ritardati, o non esserlo affatto: in ogni caso i loro quadranti debbono mostrare lo stesso tempo dopo la riunione se lo mostravano prima della separazione.
Come vedremo, con questo sillogismo Dingle interpreta malamente la relatività del moto di Galileo, che Einstein incorpora ed estende nella nuova teoria. La premessa maggiore non è corretta: è vero, tra due corpi in allontanamento costante è impossibile stabilire con certezza chi si stia muovendo, ma se un astronauta viaggia avanti e indietro tra due pianeti (interrompendo almeno una volta il suo moto inerziale) possiamo affermare in modo assoluto che almeno in un periodo egli si sia mosso. Anche la premessa minore è scorretta: il ritardo di un orologio dimostra che esso si è mosso, ma non dimostra che l'altro non si è mosso; potrebbero averlo fatto entrambi con moti diversi. La conclusione del sillogismo deve perciò essere rifiutata.
Ho fatto un copia e incolla di un sillogismo non mio ovviamente,che indica come ci siano aspetti che vanno approfonditi come quello di Enzo che cerco di studiare in maniera non superficiale.
Dici bene Gianni... il paradosso dei gemelli lascia ancora la possibilità di sollevare risvolti ambigui e/o oscuri.
Il guaio di questa visione legata a riflessioni spesso profonde e tipiche di studiosi accaniti e preparati è che è ben diversa dalla non comprensione che manifestano tanti personaggi impreparati. Pensa che perfino la visione di Feynman è stata criticata, ma con ragionamenti di sicura validità, anche se si sono rivelati bolle di sapone. Avevo letto un'accusa drastica contro di lui, non condivisibile magari, ma sicuramente ben argomentata. Anche Einstein ha cercato di distruggere la MQ e c'è riuscito per lungo tempo prima che si dimostrasse l'entanglement in modo decisivo.
Quello che cerco di fare io è di eliminare i dubbi che derivino da errori madornali o da insufficiente preparazione. Non posso certo portare prove decisive su riflessioni che vanno al di là delle mie possibilità e che hanno tenuto in scacco molti scienziati di primo piano per lungo tempo o che non sono ancora state sgretolate del tutto. Sai, io mi fido di Einstein (anche se ha sbagliato molto, a volte accorgendosene per primo, a volte in ritardo) dato che le osservazioni continuano a dargli ragione! Un piccolo-grande atto di fede!!! Lo stesso che uso con Feynman...
Secondo Paul Davies ( Nel suo libro "I Misteri Del Tempo") riporta questa considerazione di Einstein. "La soluzione è data dal fatto che le prospettive dei due gemelli non sono completamente simmetriche. Per compiere il suo viaggio uno dei gemelli deve accelerare, partendo dalla terra, viaggiare a velocità costante per un certo periodo, fermarsi, girarsi, riaccelerare, viaggiare di nuovo a velocità costante e, finalmente, fermarsi sulla terra per incontrare il suo gemello rimasto fermo sulla terra. Tutte le manovre del gemello viaggiatore precludono la simmetria. I diversi sistemi non sono in moto uniforme. Tenendo conto di ciò sarà il gemello viaggiatore ad essere più giovane". Fin qui mi sembra di aver capito tutto, non capisco perché ostinarsi a volerlo spiegare solo con la R.R. Siamo sicuri che l'accelerazione per portare il gemello viaggiatore a velocità prossima a quella della luce, la successiva decelerazione, l'accelerazione e la decelerazione finale si possano trascurare?
Ciao Gimar, io trovo molto semplice la rappresentazione del paradosso dei gemelli in RR in questa immagine usata da Enzo in un articolo scritto anni fa in un altro sito: col diagramma di Minkowski appare evidente che il cambiamento del sistema di riferimento è sufficiente a spiegare l'apparente paradosso
Caro Gimar,
aggiungo qualcosa che dimostra proprio il perché di questo articolo...
Come dico nel testo, è piuttosto facile risolvere il paradosso usando la RR e trascurando accelerazioni e decelerazioni. In realtà, usando l'invariante introdotto da Minkowski puoi benissimo estrapolare l'andata e ritorno con una curva che quindi contempla una variazione continua della velocità ottenuta da tanti trattini e poi passando all'integrale. Il succo di tutto si riassume nella frase : la geodetica è la traiettoria di tempo massimo. Il che dice chiaramente che si sta realmente fermo o si muove di moto rettilineo ha l'orologio più veloce.
Tuttavia, si legge spesso e lo dici anche tu: "Ma perché non usare la RG e via?" proprio perché a parole sembra facile, ma in pratica è molto meno semplice dimostrare la faccenda. Accelerazioni, decelerazioni vanno trattate insieme alla RR e, come hai visto nel filmato, la soluzione non è ovvia, anzi, e per farla sembrare tale è necessario commettere errori o nascondere qualcosa. Io ho usato l'approccio di Feynman, ma alcuni lo hanno confutato e ancora oggi la disputa è accesa. Lo stesso Einstein non è mai stato realmente convinto della spiegazione...
dico la mia opinione con umiltà: in questi quattro anni , da quando mi interesso alla relatività, pensavo di aver capito una cosa; non c'è alcun paradosso nella storia dei gemelli, però il paradosso vero e proprio, cioè quello che dice che entrambi devono essere più giovani dell'altro, per me è ambito della RR, così come lo aveva concepito il filosofo-fisico che per primo lo ha espresso, interèpretando erroneamente i sistemi inerziali (ovvero non tenendo conto che un0 dei due sistemi non è inerziale)Per quanto riguarda invece la differenza di età, bisogna calcolare in ogni caso la differenza fra la lunghezza di due linee (che potrebbero non essere necessariamente geodetiche) per avere la differenza fra i tempi. Ma questo si può fare con la geometria dello spazio tempo, sia in RR che in RG
caro Umberto, io sono abbastanza d'accordo con te.. ma devo puntualizzare una tua frase:
"però il paradosso vero e proprio, cioè quello che dice che entrambi devono essere più giovani dell'altro..."
Il paradosso non è questo. Il paradosso è che, malgrado si sia in RR, uno è effettivamente più giovane dell'altro.
Scusa della puntualizzazione, ma qualcuno potrebbe capire male e fare confusione...
é proprio questo il punto , su cui forse sbaglio, io su questo non vedo alcun paradosso, ovvero che uno sia più giovane Dell altro. Questo però l ho pensato dopo anni
In RR è più che logico che entrambi pensino che sia l'altro a rimanere più giovane. Questa diversa interpretazione è esattamente il risultato della RR. Se consideriamo infiniti orologi nello spazio, sincronizzati con quello della Terra , è possibile in ogni momento vedere che per loro il gemello che viaggia è più giovane. ma è anche vero il contrario. Infiniti orologi sincronizzati con quello dell'astronauta vedrebbero il terrestre restare più giovane. Notiamo bene, però, che in questo modo abbiamo un confronto continuo che dimostra la RR, ma non abbiamo un contatto diretto dei due gemelli. Per poterlo avere bisogna cambiare sistema di riferimento e quindi, alla fine, si perde la simmetria. Questa perdita di simmetria risolve il VERO paradosso che si stupisce che uno SOLO possa essere realmente più giovane dell'altro.
aggiungo ancora...
nel caso del muone, noi vediamo le cose solo dal nostro punta di vista. Ed è quindi non paradossale che il muone sia visto vivere più a lungo. E' come se noi guardassimo i due orologi in un istante in cui entrambi si stanno muovendo in modo inerziale. Attenzione, però, questa è solo una visione. Per il muone siamo noi che abbiamo l'orologio più lento. ma nessuno gliel'ha mai chiesto? Non siamo nel caso del paradosso... Siamo nel caso in cui uno solo può dire cosa sta osservando, come quando l'orologio terrestre nello spazio verificava che l'orologio dell'astronauta andava più lento. Se avessimo chiesto all'astronauta lui avrebbe detto il contrario (così come farebbe il muone). Il paradosso nasce quando entrambi devono ammettere che solo uno è ringiovanito! Se il muone girasse in tondo, allora saremmo nel caso del sistema accelerato e nessuno si stupirebbe che lui rimanga più giovane (nemmeno lo stesso muone girovago).
si, io volevo dire proprio questo; probabilmente mi sono spiegato male. Ah, quanto più semplice è la matematica!
per Gimar,
volevo aggiungere qualcosa riguardo a Paul Davies. E' sicuramente un grandissimo divulgatore (forse ancora di più che scienziato), ma a volte si lascia prendere la mano e cerca il sensazionale... come il suo appoggio alla teoria delle 11 dimensioni dello spazio e altro ancora. In qualche modo, cerca argomenti ai confini della Scienza verificabile e poi, con la sua bravura esplicativa, le rende quasi realistiche sotto vari punti di vista. Insomma, a volte la bravura, se indirizzata verso argomenti ambigui o ancora vaghi, può essere anche un po' pericolosa...
In altre parole, Feynman era di un alto pianeta!
Enzo, ma quando qualcuno ci spiega come fa il muone ad arrivare a terra non è come se gli si chiedesse il suo punto di vista
Per fortuna non c'è il paradosso del muone, lui non cambia sistema inerziale.
E no, Gimar... Siamo noi che stiamo a terra che decidiamo se è vivo oppure no. Il suo orologio biologico rallentato si vede solo da terra. Lui risolve la questione vedendo accorciarsi la distanza che lo separa dalla Terra... lui ha vissuto una vita normale, ma la Terra gli è andata incontro velocemente e l'ha raggiunto prima che morisse...
Grazie Enzo.
figurati Gimar... è sempre un piacere cercare di risolvere dubbi a chi mostra tanto interesse!
Caro Enzo, questa discussione mi ha incuriosito, per cui provo anch'io a dire qualcosa.
Volevo proporre una piccola rappresentazione grafica per descrivere ciò che mi immagino nel momento dell'inversione di rotta del gemello astronauta.
Una rappresentazione, da prendere con le pinze, poiché non ho idea se la seconda parte sia corretta.
Nella prima figura (diagramma di Minkowski) viene ritratta un'astronave che per la Terra viaggia a 0,9 c, con un percorso di andate e ritorno e relativi assi del tempo T' (andata) e T'(ritorno) e soprattutto relative linee di simultaneità.
In questa rappresentazione che usa solo la RR, volevo soffermarmi, però, su cosa accade quando l'astronave inverte la rotta.
Quando giunge alla fine del viaggio di andata l'orologio dell'astronave segna 2 anni, mentre la linea di simultaneità (ossia gli orologi sincronizzati solidali con il percorso di andata dell'astronave) segnalano che l'orologio della Terra segna 0,872 anni.
Quando riparte ed inverte la rotta (il suo orologio segna una frazione infinitesima di tempo in più di 2 anni), mentre la linea di simultaneità (ossia gli orologi sincronizzati solidali con il percorso di ritorno dell'astronave, che sono diversi da quelli del percorso di andata) segnalano che l'orologio della Terra segna 8,298 anni.
Con l'inversione di rotta si determina un salto temporale...
Ovviamente tutti gli eventi terricoli inferiori a 8,298, sono stati simultanei con il passato del percorso di solo ritorno dell'astronave (asse T' ritorno prima che il suo orologio segnasse 2 anni), mentre tutti gli eventi terricoli successivi a 0,872 anni risulterebbero simultanei con il futuro del percorso di un'ipotetica astronave di sola andata (asse T' andata dopo che il suo orologio segna 2 anni)...
Già, ma un'astronave non ci mette proprio un tempo pari a zero per invertire la rotta a quella velocità.
Possibile che non ci sono linee di simultaneità dell'astronave che coprono anche quell'intervallo che va da 0,872 a 8,298 anni terricoli?
L'idea è quella perciò di rappresentare anche la decelerazione e l'accelerazione, come una continua modifica degli assi del tempo e di quelli di simultaneità (io ne ho rappresentati solo alcuni, ossia: V=0,9 c; V=0,6c; V=0,3 c; V= 0; a V=-0,3c; V=-0,6c; V=-0,9c).
Il risultato è questa figura.
Se il ragionamento e la rappresentazione (solo grafica ed approssimativa) sono corrette, nella fase di inversione di marca, sia durante la decelerazione, sia durante l'accelerazione il tempo dell'astronave scorre molto più lentamente rispetto a quello della Terra visto dall'astronave..
L'apice si raggiunge quando la velocità risulta uguale a zero e per un istante le linee di simultaneità dell'astronave e quella del Terricolo sono identiche...
Usando molte più velocità di quelle indicate nella figura si dovrebbe coprire tutto l'intervallo di tempo terricolo da 0,872 a 8,298.
Guardando il video, se non ho compreso male, viene introdotta una gravità fittizia per simulare l'accelerazione....
Se guardo il grafico che ho descritto, però, lo stesso rallentamento del tempo avviene sia in fase di decelerazione sia in fase di accelerazione...
Come interpretare ciò con quanto suggerisce il video?
Sembra come se la gravità eserciti solo un azione frenante rispetto alla velocità di 0,9 c, un'azione che si intensifica quando l'astronave rallenta (con conseguentemente “rallentamento” del tempo dell'astronave rispetto a quello della Terra), che raggiunge il suo apice quando l'astronave è ferma (rispetto alla Terra) e diminuisce “gradualmente” di intensità finché l'astronave non raggiunge la velocità di crociera di v=-0,9c.
Mi lascia un po' perplesso come l'astronauta possa continuare a ritenersi fermo..
Ammettiamo di accelerare un'astronave in 10 secondi da 0 a 0,9C, sarebbe difficile staccare dalla parete posteriore l'astronauta...certo non potrebbe più accorgersi di nulla...
Ammettiamo allora di diluire questa accelerazione in un intervallo maggiore di tempo e che per qualche strano motivo l'astronauta non avverta alcuno scossone.
Durante l'accelerazione tutto ciò che prima era alla stessa distanza ora sembra muoversi con una certa velocità ... non si tratta però dell'astronauta che vede la Terra che si allontana o del terricolo che vede l'astronave che si allontana, ma tutto, proprio tutto... (la Luna, il Sole, le Stelle, le Nebulose) continua a cambiare distanza .. è l'intero precedente sistema di riferimento che continua a mutare.... sembrerebbe un buon indizio per concludere che sono io che ho cambiato sistema di riferimento e non viceversa...
Scusate la lunghezza
e come dicevo all'inizio non ho idea se la seconda parte della descrizione sia davvero corretta (oltre che approssimativa e giusto per dare un'idea).
Paolo
Caro Paolo,
il tuo ragionamento in qualche modo funziona, dato che riesce a rendere non simultaneo il salto del tempo. Il problema è che se ti consideri puramente in RR, lo devi accettare. Puoi fare il tentativo di integrare tanti piccoli cambiamenti di rotta a velocità costante e ricadi nella descrizione dell'invariante, il quale, in fondo, dice proprio quello che dici tu: durante la manovra curvilinea ottieni un rallentamento che è quello che farà sempre essere il tempo proprio minore rispetto alla linea rettilinea. Noi abbiamo sempre trattato due linee soltanto, ma si può, integrando con dt piccolissimi, simulare un cambiamento curvilineo. Resta comunque un fenomeno di RR che cerca di simulare un moto decelerato e accelerato. Tu, in fondo hai proprio descritto questa fase.
Se però introduciamo la possibilità che esista un sistema non inerziale (RG), tu te ne devi sempre accorgere e la frase che segue non ha senso:
Ammettiamo allora di diluire questa accelerazione in un intervallo maggiore di tempo e che per qualche strano motivo l'astronauta non avverta alcuno scossone.
Il fatto che lui veda girare non solo la Terra, ma tutto l'Universo non è sufficiente (secondo me) per fargli pensare che è in movimento. Lo potrebbero essere Le stelle , il Sole e tutto il resto che fa parte del sistema Terra e quindi è ovvio che si muova tutto.
Secondo me, ha ragione Feynman quando dice che vive di più che SENTE di non essere fermo, ma per sentirlo deve sentire un'accelerazione, altrimenti puoi sempre pensare di essere in moto uniforme...
Feynman dice: "Si chiama paradosso solo per coloro che credono che principio di relatività voglia dire che TUTTI i moti siano relativi. Tuttavia, quando l'astronauta si deve girare per tornare, gli capitano cose stranissime, come il motore che si accende, le cose che cadono sul pavimento o sulle pareti, ecc. E' costretto ad ammettere che non è più in moto uniforme. Il compagno terrestre, invece può dire senza alcun problema che non ha mai sentito questi strani avvenimenti...".
Il muone in laboratorio è un caso lampante...
Comunque, la tua analisi mi sembra giusta, ma direi che continua a svolgersi nella RR, anche se accetti una variazione continua della direzione...
Eh sì, il paradosso dei gemelli è cosa veramente inutile, in fondo in fondo... Una riflessione teorica che crea soprattutto confusione. La realtà è che nel caso della RR si risolve facilmente in molti modi e con la RG si entra nei sistemi non inerziali che differiscono da quelli inerziali e ce ne se può accorgere.
caro Paolo e cari TUTTI,
secondo me il metodo migliore per seguire passo a passo il paradosso dei gemelli nella RR è quello che trovate nell'approfondimento su Minkowski, nel capitolo: Manteniamo il contatto visivo e il paradosso si dissolve. Il metodo è quello più comprensibile, dato che vi è sempre il contatto diretto tra i due gemelli. Non si notano nemmeno salti strani... Tutto, in pratica, si risolve con l'effetto doppler relativistico. Per un certo periodo la luce che arriva a terra è inviata da un astronave che si allontana; nel secondo periodo, avviene il contrario: la sorgente della luce si avvicina. Attenzione: è un vero effetto doppler e non ha niente a che vedere con il redshift.
Sicuramente (spero) ci torneremo sopra andando avanti con l'aberrazione luminosa. Per adesso stiamo trattando di un moto decisamente lento (classico) dovuto alla Terra che gira intorno al Sole. Tuttavia, è facile capire che potremo utilizzarla per una viaggiatore a grande velocità, da cui segue che le direzioni delle stelle intorno a lui cambiano inclinazione rispetto alla direzione del moto, ma che devono anche subire redshift a causa del moto relativo tra sorgente e astronave. E ricordiamo che redshift vuol dire cambiamento di frequenza, ossia cambiamento del tempo misurato da un orologio... come avevamo descritto nella parte finale della RG...
Vi invito perciò a seguire con attenzione gli articoli sulla aberrazione: serviranno per capire molto meglio cosa si vede viaggiando ad alte velocità... non per niente sto continuando a girarci intorno per rendere il fenomeno il più intuitivo possibile (e non perdetevi, dopo una puntata un po' noiosa, l'avventura mitologica tra uno spartano e un ateniese...
)
Sara è sempre vissuta in un sistema inerziale Adam certamente no, poiché Egli NON si è mosso sempre di moto rettilineo uniforme rispetto al suo pianeta madre. Per allontanarsi da questo fino alla velocità di crociera vicina alla velocità della luce deve prima accelerare fortemente, poi decelerare una volta giunto a destinazione, quindi ruotare intorno alla stella lontana, riaccelerare e poi rallentare fino a fermarsi sul nostro pianeta. Adam è dunque vissuto per anni entro un sistema accelerato, del quale la Relatività Ristretta non si occupa. Un'analisi completa di questo paradosso in tutti i suoi dettagli può quindi essere svolta solo nell'ambito della Teoria della Relatività Generale, nella quale si mostra che, in presenza di accelerazioni e decelerazioni, il tempo viene "oggettivamente" rallentato rispetto a quello di un sistema inerziale!!!
Se il video finiva prima dell’ultima affermazione sarebbe stato meglio.Credo che l’autore abbia scambiato la simmetria che c’è nel calcolare gli anni che i protagonisti calcolano dal loro personale punto di vista,in rapporto all’informazione che la luce trasporta loro ,con l’invarianza che è un’altra cosa.
A volte penso alla velocità della luce che passa vicino ad un interruttore della luce e la accende,poi la luce vecchia e la luce nuova corrono in pari,in pari?e passando vicino ad un altro interruttore accende un altra sorgente di luce.Poi penso a come la luce si comporta con la luce,essa viaggia in maniera inerziale quando accende la luce.Lo so che è un limite invalicabile.Boh!
Caro Gianni... meno male che i fotoni non hanno abbastanza forza per schiacciare un interruttore, altrimenti ne vedremmo delle belle!!!
Anzi, prima o poi so che Daniela ha in serbo un racconto sui buchi neri che si avvicina alla tua descrizione... ma c'è troppa carne che cuoce nel Circolo e bisogna mettersi in coda...
L'ho pubblicato un'ora fa...
ma se questo non è "filing" (alla Pautasso...) che cos'è ????
Eh sì... riusciamo quasi a leggerci nel pensiero... alla faccia della "praivasi"!!! Quasi quasi chiedo a Oreste Pautasso di scrivere al Garante affinché tuteli i nostri pensieri!
(Non ci fate caso, cari lettori, non siamo impazziti... o forse sì?
)
Ma no, Daniela...
il nostro motto è :"Semel in anno licet resipiscere (?)" Quindi, prima o poi diremo anche qualcosa di serio... un premio a chi indovinerà quel momento!
Resipiscente re-si-pi-scèn-te Che si ravvede da un errore
dal latino: resipiscere ravvedersi, propriamente riprendere i sensi.
Si tratta di voce dottissima, molto rara e strana, da trovare. È un ravvedersi che è quasi un rientrare in sé, un rinsavire che riporta sulla retta via. Avrebbe anche una bella immagine ed è molto difficilmente sostituibile, ma la rarefazione dei casi in cui si può usare la esilia nei testi normativi o del registro aulico.
Di' la verità... la sapevi o l'hai cercata con Google???
In realtà mi sembrava di ricordarlo... ma non ne ero sicuro, da lì il punto interrogativo... il classico colpo di fortuna (non voglio infierire
)
No, no... è giusto dare a Cesare quel che è di Cesare, ci mancherebbe! Onore al merito!!
Non si diventa professori per caso
Proprio oggi ho letto su Facebook di un signore,che ha una età apparentemente ormai aulica,che ha preso la sua settima laurea.Ha detto che lo ha fatto per farsi una cultura.Almeno siamo sicuri che ha imparato a contare fino a sette!
Notiziona: http://www.ansa.it/scienza/notizie/rubriche/spazioastro/2017/01/30/gemelli-spaziali-non-sono-piu-identici-primi-dati-missione-_57548d5a-5740-42ef-b14b-d5c2c4013300.html
Magari non è più giovane ma sicuramente è diverso
Torno serio! Leggendo "Sei pezzi meno facili" di Feynman a proposito del paradosso dice che nel moto rettilineo non abbiamo modo di sapere a che velocità stiamo viaggiando senza un riferimento esterno. Quindi possiamo dire che non esiste una velocità "assoluta" salvo che per i fotoni? Questo non dovrebbe complicare la comprensione di quale dei due gemelli è invecchiato, visto che la velocità è solo relativa e il gemello rimasto a terra potrebbe anche avere una velocità molto elevata (insieme alla terra!).
Ciao Gimar,
in attesa che ti risponda il prof., credo che il problema non sia quello di chi si muove (in RR entrambi possono considerarsi fermi e credere che sia l'altro a muoversi), ma di chi rompe la simmetria cambiando il sistema di riferimento e non c'è dubbio che questo accada solo al gemello sull'astronave nel momento in cui inverte il senso il marcia.
Daniela, la contrazione dei tempi è legata al rapporto v/c al quadrato. Quindi la velocità v deve essere paragonabile alla velocità della luce (velocità vera non relativa), ho aggiunto questo per chiarire il mio dubbio.
caro Gimar,
non ho capito bene qual è in realtà la tua domanda. Ripeto però il succo del problema sollevato da Feynman: solo chi si accorge di essere in movimento invecchia di meno. E questo può essere capito solo se si subisce un'accelerazione, altrimenti nessuno può dire se si muove oppure no. Ovviamente, affinché gli effetti siano visibili le velocità devono essere relativistiche. Io, se comincio a correre sempre più forte rispetto a mia moglie invecchio di meno senz'altro, dato che subisco un'accelerazione... ma sfido chiunque ad accorgersene...
Se il concetto era un altro, fammelo sapere...
Grazie Enzo. Immaginiamo che i due gemelli siano su di una astronave che viaggia a velocità relativistica. Uno dei due sale su una scialuppa e si allontana a velocità sempre relativistica (per esempio in direzione contraria). Solo quello che sale sulla scialuppa è consapevole di muoversi, per le solite accelerazioni. Chi invecchia?
Così il dubbio dovrebbe essere più chiaro.
Eccomi...
Invecchia di meno chi prende la scialuppa e poi torna nell'astronave. L'astronave è in moto rettilineo uniforme così come viene considerata la Terra in prima approssimazione. La scialuppa è l'astronave che accelera per andarsene e che poi torna alla base.
Non c'è alcun problema sul fatto che entrambi siano d'accordo. Chi sta sull'astronave , per la sola RR, conclude che è l'altro che deve invecchiare di meno. Lui può anche non sapere che la scialuppa accelera, ma per lui, che applica la RR, chi viene visto viaggiare invecchia di meno. Chi è sulla scialuppa si accorge di accelerare e, quindi, sa che sta rompendo la RR e che deve restare più giovane.
Come sappiamo, però, entrambi potrebbero concludere lo stesso anche senza accorgersi di accelerazioni, ma ragionando sul cambiamento di sistema di uno solo. Con l'accelerazione si ottiene lo stesso risultato, ma si entra nella RG...
Grazie Enzo sempre gentile e disponibile
Scusate il ritardo,
mi ci è voluto del tempo per riuscire a trovare un modo per affrontare questo (non)paradosso. C'è stato molto da imparare.
In sostanza concordo con quanto dicono Enzo nell'articolo e Daniela e Paolo nei loro commenti. Provo a dire i miei argomenti che riprendono ed in parte estendono quelli di Paolo. Alla fine aggiungo una considerazione sull'effetto del campo pseudo gravitazionale sul gemello stanziale affermato nel video che sembra contraddire Enzo, ma in realtà conferma che questo effetto non c'è.
La trattazione più semplice del problema è quella con il gemello viaggiatore che si allontana a velocità costante dall'altro gemello per metà del viaggio e per l'altra metà fa il percorso inverso a velocità uguale ed opposta a quella dell'andata. Daniela e Paolo hanno fatto vedere i diagrammi relativi e le linee di simultaneità del gemello viaggiatore nel sistema di riferimente del gemello stanziale.
Certo, può sembrare poco realistica quella inversione istantanea di verso tra il viaggio di andata e quello di ritorno. L'accelerazione tendente all'infinito in quell'istante fa venire qualche dubbio. Forse appare più realistico un passaggio graduale tra i due sistemi di riferimento con una accelerazione finita.
Il video cerca di spiegare le "peculiari conseguenze", come le definì Einstein già nel 1905, di questa accelerazione facendoci mettere nel sistema di riferimento del gemello viaggiatore. La scelta può essere discutibile poiché è il riferimento più difficile da trattare essendo non inerziale.
Ma questa scelta non è obbligata. Per descrivere il problema si può ancora utilizzare il sistema di riferimento del gemello stanziale che non subisce accelerazioni.
In questo sistema di riferimento la linea d'universo del gemello stanziale è l'asse verticale. La linea d'universo del gemello viaggiatore è invece composta da 5 tratte. Ci sono le due rette (nere) dei percorsi fatti a velocità costante nell'andata e nel ritorno. Queste due rette sono raccordate tra loro e con la linea d'universo dell'altro gemello con curve per i periodi nei quali è presente l'accelerazione alla partenza, all'arrivo e nella inversione di rotta. Queste curve sono iperboli se supponiamo l'accelerazione costante. Anche qui è possibile tracciare le linee di simultaneità (verdi) di istanti equidistanti per il gemello viaggiatore che evidenziano lo scorrere più lento del tempo di questo gemello in presenza dell'accelerazione. Questo grafico non è solo qualitativo. E' infatti possibile ricavare il tempo dei due gemelli dalla lunghezza (relativistica) delle loro due linee d'universo. In più conferma che non ci sono sorprese nel repentino cambio di riferimento nei diagrammi di Paolo, quando i 3 periodi accelerati diventano trascurabili rispetto agli altri due (accelerazioni grandi o lunghi periodi a velocità di crociera) il risalutato tende a quello con i diagrammi visti nel commenti di Daniela e Paolo. Tutto questo può essere ricavato applicando solo la RR, comprese le tratte accelerate. Lo ha detto più volte Enzo e seguendo questo ragionamento ho potuto verificarlo direttamente.
La scelta del video di mettersi nel sistema di riferimento del gemello viaggiatore crea parecchie complicazioni già nella sola definizione del sistema di riferimento. Inevitabilmente si sconfina nella RG. Tanto che, stringi-stringi, il video dice solo che l'effetto è dovuto alla accelerazione che è equivalente alla gravità, non mi sembra ci sia altro. Sull'effetto della pseudo gravità credo ci sia la maggiore imprecisione del video. Per quanto ho capito, è vero che in quel sistema di riferimento tutti gli oggetti sono soggetti ad una pseudo gravità anche quelli più remoti e che questo effetto dipende dalla posizione. Apparentemente mi metto contro a quanto dice Enzo, se non fosse per un fatto che il video ignora. Il gemello stanziale è in caduta libera in questo campo pseudo gravitazionale e quindi, proprio per il principio di equivalenza, il suo tempo viaggia come in un riferimento inerziale e non è influenzato dal campo pseudo gravitazionale come dice il video. Non poteva essere altrimenti. Il tempo proprio non dipende dal sistema riferimento. Alla fine non mi sembra che affrontare il problema nel riferimento non inerziale del gemello viaggiatore aggiunga veramente qualcosa alla comprensione del fenomeno.
caro Fabrizio,
concordo abbastanza con te. Utilizzare la pseudo gravità ed estenderla fino alla Terra mi sembra un metodo poco plausibile, in effetti, anche se so che molti si sono rifatti a questa spiegazione (continuo, però, a non concordare sulla decelerazione trascurata: o tutto o niente). Anche persone più che qualificate... Io continuo a preferire una RR a scatti per ammorbidire il cambiamento simultaneo di riferimento... o, ancora meglio, l'invio continuo di segnali luminosi... De gustibus...
Tra parentesi, non so se hai ricevuto il msg... quando vuoi, vai pure con la lagrangiana...
Enzo scusa l'insistenza su questo punto, vorrei capire meglio la tua affermazione riguardo il campo pseudo gravitazionale.
Per il 50% trovo argomenti per condividerla e per il 50% argomenti che vanno in senso contrario, come si conciliano tra loro non lo so.
Se mi metto in un riferimento accelerato in condizioni non relativistiche devo considerare delle forze apparenti che vanno fino all'infinito. Nel caso di movimento rotatorio addirittura l'accelerazione è crescente con la distanza. Quacosa di simile dovrei aspettarmi anche in RG, almeno come limite non relativistico.
Per contro questo campo è solo apparente. Se scegliessi un riferimento inerziale non esisterebbe. Per questo non può avere effetti su grandezze reali non dipendenti dal riferimento come il tempo proprio. Non basta dire che non ha effetto sugli oggetti in caduta libera, come ho detto nel post precedente. Non dovrebbe avere effetti reali in nessun caso, anche per corpi non in caduta libera, indipendentemente dalla loro distanza.
In rete ho trovato qualcosa sulla forma di questo campo apparente nel caso di accelerazione uniforme che sto cercando di capire. Ancora nulla di esplicito sui suoi effetti reali. Forse ciò che mette insieme il tutto è che si dice che anche per il riferimento accelerato lo spazio è piatto nonostante questo campo pseudo gravitazionale. Cosa a posteriori ovvia, ma che non mi aspettavo.
caro Fabry,
se leggi la parte della RG riguardante gli orologi, vedrai che un sistema accelerato equivale a un campo grav. Si dimostra facilmente che il tempo di chi è più lontano nel verso del moto ha l'orologio che gira più velocemente. L'astronauta è più vicino della Terra e quindi il suo orologio rallenta durante l'accelerazione scombussolando la simmetria della RR. Non mi torna però la decelerazione che dovrebbe introdurre una "gravità" opposta con la Terra più in basso, ma probabilmente si può dimostrare che conta meno, non sapendo bene da dove far partire il centro della gravità fittizia...
Comunque, restano ancora grosse diatribe a proposito... Secondo me, resta anche il fatto che la Terra non fa parte del sistema accelerato... ma... tutto sta a come si vuol vedere la cosa...
Ho cercato di analizzare il punto dubbio che segnale Enzo : "Non mi torna però la decelerazione che dovrebbe introdurre una "gravità" opposta con la Terra più in basso, ma probabilmente si può dimostrare che conta meno, non sapendo bene da dove far partire il centro della gravità fittizia... "
La mia conclusione è che l'affermazione fatta nel video che genera questo dubbio è almeno fuorviante se non errata. Sottopongo il mio ragionamento al circolo per un vostra verifica.
Per prima cosa credo sia utile ricapitolare la situazione fisica.
Ci sono due oggetti, che nel video vengono personalizzati in Sarah ed Adam. All'inizio i due sono fermi rispetto ad un riferimento inerziale. In questo riferimento non ci sono campi gravitazionali che non sono necessari per produrre il (non)paradosso dei gemelli. Nel video è citata la Terra, ma il suo effetto gravitazionale è sempre trascurato.
Sarah rimane ferma rispetto a questo riferimento. Lo possimo quindi chiamare riferimento di Sarah. Adam invece prima si allontana da Sarah per un periodo poi inverte la rotta e ritorna da Sarah. In questo percorso Adam accende i razzi 3 volte: partenza, inversione di rotta e arrivo.
Il dubbio indicato da Enzo credo si applichi a questa tesi sostenuta dal video.
Il video sostiene che la causa del differente fluire dei tempi propri di Sarah e Adam è la differente posizione dei due nel campo gravitazionale uniforme equivalente alla accelerazione di Adam prodotta dalla accensione dei razzi.
Mi riferisco al tempo proprio perché è il tempo scandito dall'orologio fisico e biologico dei due personaggi. Per accelerazione intendo il vettore accelerazione che può produrre una accelerazione, intesa come incremeto di velocità, o una decelerazione.
Questa tesi del video credo sia almeno fuorviante se non errata proprio nel caso del campo uniforme trattato nel video. Sono arrivato a questa conclusione per queste due ragioni:
Per dimostrare queste mie due affermazioni ricorro ad una caratteristica fondamentale del tempo proprio in RR e RG. Il tempo proprio è una grandezza sulla quale tutti gli osservatori sono d'accordo. Questo significa che può essere calcolato rispetto a qualsiasi riferimento ottenendo lo stesso risultato.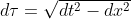
. t ed x sono la coordinata temporale e spaziale del riferimento, quest'ultima la prendo allineata con la direzione del moto di Adam.
Allora li calcolo nel riferimento di Sarah dove è più semplice. Questo è un riferimento inerziale dove l'elemento di tempo proprio di un corpo calcolato lungo la sua linea d'universo è dato da
Tempo proprio di Sarah
In questo riferimento Sarah è ferma. Il tempo proprio di Sarah (τS) coincide con la coordinata temporale, τS=t, poiché dx=0. Questo mi sembra dimostri la mia prima affermazione.
Tempo proprio di Adam
Il calcolo del tempo proprio di Adam è leggermente più complesso. In presenza di una accelerazione uniforme la linea d'universo di Adam è una iperbole.
La sua equazione è del tipo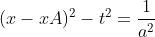
.
xA è un parametro che allontana la curva dall'origine del riferimento dove si trova Sarah. Questo parametro ci serve per capire se il tempo proprio di Adam dipende o meno dalla distanza da Sarah.
L' equazione si può sviluppare per ottenere il tempo proprio di Adam:
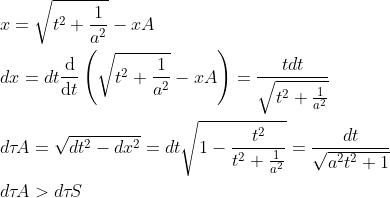
Il tempo proprio di Adam (τA) non dipende dalla distanza da Sarah. Inoltre non dipende dal verso di a, ne se a produce un incremento o decremento della velocità. Questo credo dimostri la mia seconda affermazione.
grazie Fabrizio,
come sempre attento, preciso e collaborativo! Il concetto che esponi è molto saggio, direi: La RR è una trasformazione simmetrica, mentre la RG non è simmetrica. Non è che il mondo circostante subisca gli effetti di chi è in gravità. Il fatto di pensare che tutto l'Universo sia legato a quell'effetto mi lascia molto perplesso... In altra parole, se io accelero rispetto ad A, subisco certi effetti se visto d A. Ma non è vero che A sia simmetrico come nella RR e debba subire gli stessi effetti, ossia che A sia accelerato nel mio sistema di riferimento.
Forse, sarebbe meglio dire che mentre decelera e accelera vicino all'ipotetico punto di ritorno, la RG impone che il suo orologio rallenti sempre di più in certe configurazione rispetto a quello del moto uniforme.In altre parole, invece di un salto netto si avrebbe un salto smussato come Fabrizio ha già chiaramente enunciato.
grazie Fabry
Buongiorno a tutti.
Domanda... Ma perché possiamo dire che chi sta sulla terra si considera fermo perché non soggetto ad accelerazione, visto che chi sta sulla terra è sottoposto a gravità e dunque si trova in un sistema accelerato?
Grazie
caro Michele,
vista la velocità insignificante della Terra, possiamo approssimarlo con un moto inerziale.
Ok chiaro la velocità della terra è insignificante, ma io sto pensando agli effetti della sua massa ... Questa genera un campo gravitazionale, dunque per il principio di equivalenza è come se il sistema di riferimento del gemello terrestre fosse sottoposto ad accelerazione costante non trascurabile ...
Grazie!
Gli effetti della massa non comportano velocità abbastanza alte da poterla trascurare. E come se volessimo tener conto della Terra nell'accelerazione dell'astronave...
ok grazie,
Vediamo se ho capito:
partiamo dal mio dubbio di fondo: dopo aver letto le due frasi "chi subisce gli effetti di un’accelerazione o decelerazione sa benissimo di non essere in un sistema inerziale e quindi sa benissimo di muoversi" e "chi sta fermo continua a sentirsi fermo e quindi non può che concludere che sia il viaggiatore a invecchiare di meno. " mi sono chiesto: come fa il gemello terrestre a considerarsi fermo rispetto a quello che viaggia sull'astronave?
risposta: anche se il gemello "terrestre" è immerso in un campo gravitazionale e dunque sottoposto ad accelerazione costante (se lascia andare una pallina questa non rimane ferma in aria ma cadrà ai suoi piedi ) tale accelerazione è debole, e dunque possiamo approssimare il suo sistema di riferimento con un sistema inerziale non sottoposto ad accelerazione (come se si trovasse su una stazione orbitante lontana dalla terra).
invece il gemello che viaggia sull'astronave è sottoposto a forti variazioni di velocità e dunque lui sicuramente si rende conto di essere in un sistema non inerziale e dunque di muoversi
Corretto?
grazie ancora
perfetto Michele!
In realtà, non esistono sistemi veramente inerziali (anche il Sole risente della gravità galattica e la galassia di quella dell'ammasso). Figuriamoci poi quelli terrestri. Il sistema inerziale è un'approssimazione che può essere considerata più che sufficiente quando si parla di relatività con v vicine a quella della luce.
chiaro!
ultimissima domanda: se il gemello "terrestre" si trovasse su un pianeta di massa molto elevata, e dunque con campo gravitazionale molto forte, il suo sistema non potrebbe più essere considerato inerziale corretto? e dunque potrebbe succedere che al ritorno dell'astronave, scoprisse di essere rimasto più giovane rispetto al gemello che ha viaggiato?
Grazie ancora
caro Michele,
tieni conto che qualsiasi cambiamento di sistema è sufficiente a far rimanere più giovane chi viaggia. In RR si risolve pensando che, per tornare indietro, il viaggiatore deve cambiare sistema di riferimento e quindi non sono rispettate le condizioni della RR. Si risolve facilmente anche con la RG, in quanto qualsiasi tipo di accelerazione e quindi di campo gravitazionale (indotto o reale) rallenta l'orologio in modo univoco e al ritorno rimane più giovane.
Buongiorno vorrei sollevare un ulteriore dubbio sul paradosso dei gemelli.. ogni volta che il viaggiatore decelera non fa altro che accelerare ed aumentare la sua quantità di moto.. sia quando decelera per invertire la rotta sia quando è costretto a fermarsi per tornare sano e salvo sulla terra.. questo fa inevitabilmente rallentare il suo orologio biologico a levelli esponenziali.. la vera domanda a questo punto è: come fa il viaggiatore a rallentare veramente per tornare a casa e confrontarsi col suo gemello se ad ogni sua decelerazione corrisponde ad un’accelerazione uguale e contraria?
caro Marty,
per scrivere esattamente come giochino realmente le accelerazioni e le decelerazioni nelle fasi di partenza, arrivo e ritorno avrebbe bisogno di entrare nelle formule di Einstein sulla RG. Non per niente ci si limita sempre (o quasi) alla RR per riuscire a dimostrare la non esistenza del paradosso, in quanto vi è un cambiamento di sistema e che ciò porta comunque allo stesso risultato. Secondo me il sistema migliore per entrare nella RG a piccoli passi è la figura che segue(spiegata bene nel commento di Fabrizio), dove si vede come in realtà vi sia accelerazione e decelerazione, ma anche come il percorso spaziotemporale più corto sia in realtà quello più lungo, seguendo pari pari la trattazione di Minkowski. Invece di avere un triangolo come nella RR pura e semplice, abbiamo un triangolo con gli angoli smussati, ma chi va, cambia sistema e torna indietro, rimane comunque più giovane.
Il suo orologio visto da terra , dove deve tornare, ha sicuramente rallentato e quindi lui è più giovane. Posso utilizzare la figura inserita prima da Fabrizio. Oppure puoi andare a vedere la trattazione che fa uso dei segnali di luce. In ogni modo ciò che conta è che il vero guadagno nell'età si ha durante le fasi di velocità costante (sia che si vada a sinistra o a destra la terra vede sempre rallentare il viaggiatore)...
Saluti a tutti. Sono un docente di scuola alle prese con il paradosso dei muoni. Dai libri di testo e dalle letture online mi sto confondendo ancora di più. Sembra che il moto del muone sia assoluto. Si parte dalla conoscenza della vita a riposo del muone di 2,2*10-6 s. Supponiamo di non conoscerla. L'osservatore a Terra perchè non può supporre che il muone sia fermo e che la Terra e l'atmosfera si muovono verso di lui? . In questo caso la contrazione della lunghezza ci sarebbe per il terrestre, l'incontro si avrebbe dopo 2,2*10-6 s e, sempre per il terrestre, la vita del muone è durata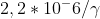
secondi. Se il muone fosse cosciente, dal suo punto di vista sarebbero passati 2,2*10-6 s mentre sulla Terra 
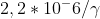. Come si risolve il "paradosso"? Help me! Grazie per questo bellissimo blog
Perdonatemi. Ho fatto confusione nello scrivere. Cerco di essere più chiaro. Se il fenomeno avviene nello spazio vuoto. L'osservatore vede la contrazione delle lunghezze ed il muone vive di meno. Dal punto di vista del muone è la stessa cosa. Dove si rompe la simmetria per dire che il muone vive meno dell'osservatore?Se sto scrivendo fesserie perdonatemi anche se sono un insegnante ma sono molti anni che non tratto questi argomenti ed ora con i nuovi programmi ministeriali queste cose si devono spiegare.
caro Paolo,
non esiste un paradosso del muone. Ciò che gli capita è perfettamente descritto dalla RR. Prova a leggere qui:
http://www.infinitoteatrodelcosmo.it/2015/04/08/le-basi-della-relativita-ristretta-o-speciale/
(la parte finale)
e magari anche qui:
http://www.infinitoteatrodelcosmo.it/2017/05/30/la-favola-muo/
questa è la realtà e tutto torna perfettamente....
Grazie mille davvero
caro Paolo, comunque, se qualcosa non ti torna, chiedi pure!
Ovviamente per arrivare al muone e alla sua strana lunga vita bisogna introdurre alla RR in generale e alle due conseguenze più importanti: dilatazione del tempo e contrazione delle lunghezze tra sistemi inerziali...
Gentilissimo Prof. Zappalà. Mi trovo perfettamente che nel riferimento inerziale solidale al muone la sua vita è sempre di 2 milionesimi di secondo mentre nel riferimento terrestre è più lunga. Mi chiedevo soltanto: sempre nel riferimento del muone, mentre trascorrono i due milionesimi di secondo di vita, lui non vede il tempo terrestre andare più lento visto che per lui è la Terra che si muove?
caro Paolo (intanto dammi pure del tu, da noi si usa così...
),
tu dici giustamente: "Mi trovo perfettamente che nel riferimento inerziale solidale al muone la sua vita è sempre di 2 milionesimi di secondo mentre nel riferimento terrestre è più lunga". Poi devi aggiungere: "Anche l'orologio dei terrestri viene visto rallentare dal muone, ma a lui poco importa. Quello che importa è che le distanze, nel sistema terrestre, per lui si contraggono e in 2 milionesimi di secondo riesce a percorrere una distanza più che sufficiente ad arrivare al suolo. Non vi è paradosso, perché per entrambi i sistemi tutto si svolge in modo perfettamente previsto dalla RR.
Ok va bene per il tu. Premesso che non svolgerò per il momento questo argomento in classe perchè devo vedere prima chi lo spiega a me eheheh. Lasciamo stare i muoni e la loro vita così breve. Si formano dal nulla degli esseri intelligenti che vivono circa 23 giorni e viaggiano alla velocità del muone in direzione Terra. Ad un anno luce di distanza ne nasce uno. Dalle trasformazioni di Lorentz il muone umano vede uno spazio minore e raggiunge giusto in tempo la Terra. Per la Terra invece impiega circa 366 giorni e tutto quadra. Tutto mi sembra chiaro. Poi però penso: il muone umano mentre viaggia misura sulla Terra un tempo rallentato e quindi si aspetta che è passato, facendo il calcoletto, poco più di un giorno sul pianeta. Invece quando arriva trova i calendari terrestri avanti di un anno. Questo è il punto cruciale che non capisco. Inoltre, se nello spazio ci sono solo il muone umano e la Terra, perchè uno misura uno spazio contratto e l'altro no? Non è come dire che è possibile scoprire in modo assoluto chi dei due si muove di moto rettilineo uniforme?
il problema è -forse- nella definizione dei due sistemi di riferimento.
la Terra e qualsiasi punto del sistema 1) ha gli orologi sincronizzati. Questi orologi vedono l'orologio del muone rallentare e anche il suo "cuore". Vedono anche il muone accorciarsi, ma questo interessa ben poco. Si accorcia solo il muone e tutto ciò che fa parte del suo sistema (ossia lui e basta). Per i terrestri la vita del muone si è talmente allungata che non possono stupirsi che arrivi al suolo.
Il muone (e il suo sistema) vede gli orologi terrestri e spaziali rallentare, ma quello che conta per lui è il proprio orologio che segna la sua vita. A lui poco importa che gli alti lo vedano sempre giovane, lui vive nel suo sistema e sa di avere un tempo di vita brevissimo. Tuttavia, il muone vede anche il sistema Terra contrarsi (tutto il sistema) e, quindi, anche la distanza spaziale tra la sua posizione nel sistema Terra e la terra stessa. Si accorcia così tanto per lui che riesce a raggiungere il suolo prima di morire.
L'importante è non pensare mai che cosa pensa l'altro che io pensi che gli altri pensino e cose del genere. Ognuno vive la sua realtà e ognuno ha lo stesso tempo proprio e lo stesso righello per misurare le distanze. Ciò che cambia, ad alta velocità, e ciò che vede un certo sistema accadere nell'altro sistema. Stiamo bene attenti a dir frasi del tipo: per chi viaggia velocemente il tempo rallenta! E' un errore gravissimo! La cosa giusta da dire è: Il sistema in quiete vede un tempo diverso da suo (rallentato) nel sistema in movimento. Come si ferma diventano un solo sistema e gli orologi iniziano a segnare lo stesso tempo. Ma questa non è più RR, dato che vi è stato un cambiamento di riferimento per il muone (prima viaggiava e poi sta fermo), mentre nel sistema Terra la Terra è sempre stata ferma (molto simile al paradosso dei gemelli).
Tutta la RR sta nel capire bene la relatività della simultaneità (per questo ho battuto a lungo su quel concetto). Da questo concetto derivano rallentamenti e contrazioni...
Tu sbagli alla fine a dire che uno vede lo spazio contratto e l'alto no. Non è vero! Solo che lo spazio tra la Terra e il muone è spazio del sistema terrestre. lo spazio del sistema muone è solo il muone. Nel suo sistema lui è fermo ed è un punto.
Tutto ciò è spiegato perfettamente (penso) nella favola del muone senza l'uso di formule. Nella RR ho inserito anche le formule. Stiamo attenti che per spiegare qualcosa a qualcuno è essenziale conoscere e capire le cose fin dall'inizio, come, ad esempio la definizione di sistema di riferimento dato da Einstein e il concetto di simultaneità relativa (oltre all'orologio di luce, ovviamente). Sarebbe ancora meglio comprendere il tutto anche usando lo spaziotempo di Minkowski, dato che riesce a sintetizzare tutta la teoria in poche linee e rende immediata la soluzione di paradossi come quello dei gemelli. Non dico insegnarlo, ma capirlo... sarebbe fondamentale
La grandezza di Einstein la si apprezza solo dopo aver cercato testardamente di capire, negli anni relativistici, le sue semplicissime formule.....
Ciao, chiedo scuso se mi intrometto, ma leggendo il testo del tuo ultimo messaggio, vorrei aggiungere una piccola cosa rispetto a quanto detto da Enzo.
Tu dici: “Poi però penso: il muone umano mentre viaggia misura sulla Terra un tempo rallentato e quindi si aspetta che è passato, facendo il calcoletto, poco più di un giorno sul pianeta. Invece quando arriva trova i calendari terrestri avanti di un anno”.
Attenzione che il “muone umano” ha il suo sistema di riferimento, per cui gli eventi non sono simultanei con quanto misura il sistema Terra.
In pratica ciò significa che se per la Terra quando il muone umano si trova ad un anno luce faccio partire l’orologio terricolo che segna tempo zero, per il sistema del muone umano l’orologio della Terra, quando nasce il muone umano, segna tutt’altro tempo... ovviamente per il muone umano la Terra si trova più vicino, ossia:
L = L0/γ).
E’ un po’ come dire che un amico del muone umano, che viaggia in solido e che ha un orologio sincronizzato con lui (stesso sistema di riferimento), che si trova a passare dalla Terra quando nasce il nuovo muone umano, vede che l’orologio terricolo segna un tempo notevolmente maggiore di zero.
Pertanto, quando è nato il nuovo muone umano, il suo sistema di riferimento indicava che l’orologio terrestre segnava un tempo molto vicino ad 1 anno e quando il muone arriva sulla Terra l'orologio terricolo segna 1 anno (bisogna considerare l’intervallo di tempo trascorso), per cui anche per il sistema del muone il tempo della Terra risulta dilatato rispetto al suo ed è pari a ΔT = Δ T’/γ.
Se ho detto qualche sciocchezza sono sicuro che Enzo mi correggerà.
Paolo
Ancora grazie a tutti. Il punto di nascita del muone ed il punto di arrivo ho capito finalmente che sono in quiete relativa. Sono punti del solido di riferimento della Terra. La contrazione tra i due punti esiste nel riferimento muonico. Inoltre, nel riferimento muonico, inizio del moto ha tempo zero ma, corrisponde a tempo = (v/c^2)D sulla Terra. D è la distanza tra partenza ed arrivo nel riferimento terrestre. Quindi, durante il moto, il muone dice che sulla Terra il tempo va più lento. La Terra simmetricamente dice che il tempo del muone è rallentato. Quando il muone vede la Terra prima di morire, vede il calendario avanti di un anno poichè quando è cominciato il moto, la Terra stava già nel futuro. Ho fatto un mix tra i suggerimenti di Enzo e Paolo.
ottimo Paolo!
comunque, siamo sempre a tua disposizione....
Gentilissimo Enzo. Sono dei veri rompicapo per me questi argomenti temporali. Ai tempi dell'università furono anche affrontati superficialmente. Con il ragionamento dell'atmosfera che è solidale all'osservatore terrestre credo di trovarmi in tutto. Cioè in questo caso il punto di partenza del muone ( A )è in quiete rispetto al punto di arrivo (B). Cioè abbiamo un punto dell'atmosfera individuabile e che rimane oggettivamente in quiete rispetto alla Terra. Per la Terra AB è fermo. Se invece esiste nell'Universo solo un osservatore ed il muone, io continuo a vedere la situazione perfettamente identica dai due punti di vista. Perchè il muone vedrebbe contratto lo spazio vuoto ed invece l'osservatore umano no? Si scoprirebbe il moto uniforme assoluto in questo caso. Giuro che è l'ultima volta che rompo dicendo cose anche ripetitive
Non c'entra l'atmosfera che possiamo trascurare viste le velocità in gioco. Quello che conta è il sistema i riferimento. Quello della Terra è il sistema che contiene, in prima approssimazione anche la Luna e il Sole e tutto l'Universo, dato che le velocità in gioco sono trascurabili rispetto a quella del muone. Il sistema di riferimento einsteniano della Terra significa un sistema che ha tutti gli orologi sincronizzati. Un punto fermo rispetto alla Terra nel vuoto, avrebbe lo stesso tempo della Terra. Il muone invece si muove. La Terra misura il punto fermo nello spazio sempre alla stessa distanza perché il righello di Einstein gli dice che è una lunghezza propria.
Ovviamente, anche il muone può considerarsi fermo, ma il suo sistema è lui stesso, a meno che non ci sia un altro muone che viaggi come lui (il sistema sarebbe il loro), ma più lontano. Per i muoni distanziati lo spazio tra di loro sarebbe una distanza propria, mentre per la Terra si accorcerebbe. Un punto (o meglio un evento) è sempre lo stesso, ma cambiano le sue coordinate x e t a seconda del sistema in cui si misura.
Il concetto fondamentale è quello dei comprendere bene cos'è un sistema di riferimento...
caro Paolo,
aggiungo...
quando esponi il paradosso dei gemelli, fai proprio quanto ho detto. La stella che raggiunge l'astronauta è sempre nel sistema terrestre e per questo sistema la distanza non cambia (si trascura il moto della stella rispetto alla Terra). Cambia invece per l'astronauta, perché nel suo sistema è tutto il sistema Terra-stella che si muove quindi la distanza si accorcia.
non ti preoccupare di chiedere... è un piacere rispondere e cercare di aiutare. Ti posso consigliare di leggere bene come si definisce un sistema di riferimento (all'inizio dell'articolone sulla RR). Ancora meglio sarebbe vedere il tutto nel diagramma di Minkowski...
Grazie. Domani proprio ci provo in classe. Ormai i libri di testo dell'ultimo anno trattano queste cose e devo prima o poi affrontarle. I diagrammi di Minkowski non ci sono sul libro però i muoni e i gemelli sono trattati, anche se in modo molto discorsivo.
caro Paolo, prova con la favola di Muo resa più seria... magari usa dei ...rappisti...
Prendiamo 2 sistemi di riferimento nello spazio senza gravità. Ci leviamo dalla relatività generale, per stare nella ristretta. Il punto A e il punto B non possono sapere se sono fermi o in movimento,ma possiedono velocità relativa. Per A è B che si muove, per B è A che si muove. Ora A inverte la rotta e torna da B,qindi è A a non essere più inerziale. Oppure B inverte rotta e torna da A,per cui B non è inerziale. Quindi? Quale dei due punti è invecchiato secondo un orologio rallentato?
Invecchia di meno quello che cambia rotta: è lui che non obbedisce più alla relatività ristretta, avendo cambiato sistema di riferimento!
Il "paradosso dei gemelli" dimostra che si verifica la dilatazione dei tempi prevista dalla RR, ma questa prevede anche una contrazione delle lunghezze. Che cosa succede per questa grandezza?
prova a fare il diagramma di Minkowski e puoi vedere cosa capita. Ovviamente, spezzato in due, dato che cambia il sistema di riferimento...
Sul paradosso dei gemelli avrei una mia personale dimostrazione...
L'ipotesi di partenza è che un gemello stia sulla Terra ed è indiscutibile che la Terra non cambi sistema di riferimento. Questo è un dato di partenza definitivo. La simmetria non può essere rispettata. Perché? Ammettiamo per assurdo che l'astronauta si creda sempre in viaggio a velocità costante. Ammettiamo anche che lui sia convinto di essere in un sistema inerziale. Se questo valesse, allora potremmo disegnare la sua traiettoria come un asse verticale (lui si crede sempre fermo). Se valesse la simmetria la Terra, però, dovrebbe allontanarsi e poi tornare indietro. Ma, per fare questo, dovrebbe per forza cambiare sistema di riferimento. Ma questo è contrario all'ipotesi di partenza, da cui segue che non vi può essere simmetria!