Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Qual è la cardinalità  del piano? A occhio e croce  ben di più di quella della retta, che ha cardinalità c, pari dunque a quella dei numeri reali. Invece avremo una gran bella sorpresa: la cardinalità del piano è uguale a quella della retta. Questo fatto è fortemente controintuitivo. Lo stesso Cantor , in una lettera a Dedekind ,dove ne riporta la dimostrazione, scrive: "Lo vedo, ma non lo credo".

Premettiamo innanzitutto che possiamo limitarci a confrontare il segmento unitario con il quadratodi lato unitario. Infatti abbiamo  visto nell'articolo sulla Cardinalità di R che [0,1] ha la stessa cardinalità  di R; se consideriamo adesso il quadrato [0,1] x [0,1]e la funzione biunivoca in R x R  così definita:(x,y)---> (f(x),f(y)) che è costruita quindi partendo dalla funzione biunivoca f.

essendo quindi |R|=| [0,1]| e |R x R |=| [0,1] x [0,1]| possiamo limitarci a confrontare il segmento unitario con il segmento unitario.

Ci sono più modi per fare questo confronto, noi cominceremo con la curva di Peano-Hilbert, per poi analizzarlo (nel prossimo articolo) in modo più generale usando il lemma di Zorn. Lo facciamo anche per introdurre un argomento un po'curioso, quello delle curve frattali, che lo stesso Hilbert definì "curve mostruose".

Se pensiamo ad un coperchio di una scatola , e ad una corda con un certo spessore, possiamo piegare la corda in tanti tratti e occupare tutta la superficie del coperchio, con una certa lunghezza finita. Questo perchè la corda ha un certo spessore. Ma possiamo farlo anche con una corda senza dimensione? Si, anche se in questo caso la corda  non avrà una lunghezza finita.

L'idea è quella di generare una curva che riesca a coprire tutti i punti del piano. Tale curva è nota come curva di Peano-Hilbert, ed è una curva generata con un metodo ricorsivo. Riporta entrambi i nomi dei due matematici, perchè fu concepita da Peano e poi perfezionata da Hilbert.

Il nostro intento è quello di trovare un metodo per disegnare una curva (ovvero una linea continua) che copra tutti i punti del quadrato; non certo disegnarla perchè è impossibile. Ma fornire un algoritmo da dare in pasto a un calcolatore per ottenere immagini approssimanti come la seguente:

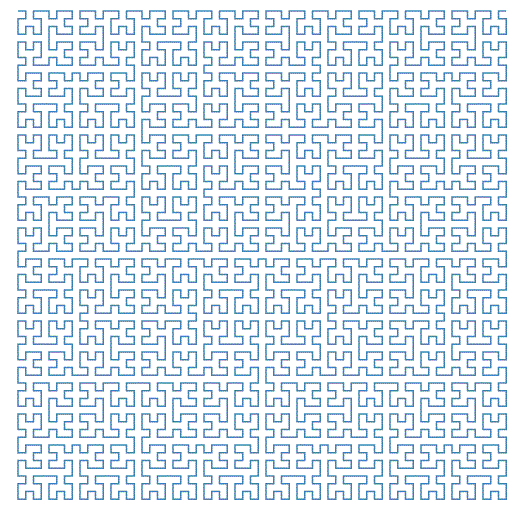
Ci sono diversi algoritmi per disegnare la curva di Peano; il modo più semplice a mio avviso per disegnare la curva  è cominciare dividere il quadrato iniziale di lato uno in quattro quadratini di lato 1/2; dobbiamo riempire tutto il quadrato in modo ricorsivo; consideriamo i centri di questi quattro quadrati e uniamoli ottenendo l'elemento base:

 

 

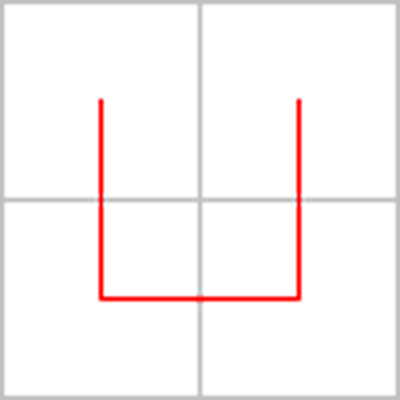
Vogliamo adesso costruire il secondo passo; divido il quadrato in 16 quadratini; devo replicare partendo dall'elemento base, quindi disponendolo su i quattro quadrati più grandi;

 

 

 

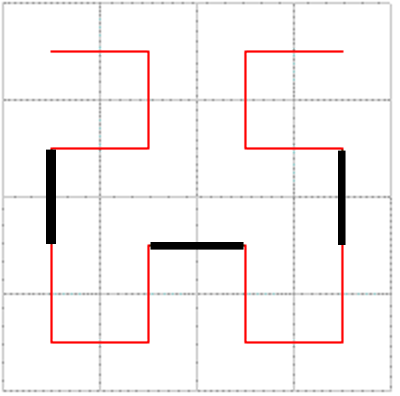
voi capite che questo equivale a congiungere i centri dei sottoquadratini; ma in che ordine? Dobbiamo costruire una poligonale; un modo può essere mantenere nei due quadrati inferiori lo stesso orientamento dell'elemento di base, e ruotare i superiori di 90° in modo opportuno; Infatti poi dobbiamo connettere (segmenti neri) gli elementi per ottenere una poligonale; se ruotassimo per esempio di 90° a destra l'elemento del primo quadrante in alto, non riusciremmo a chiudere la poligonale.

Adesso che abbiamo a disposizione un elemento base un po' più grande, continuiamo con la costruzione;  riportiamo la costruzione 2 (ridotta di un quarto) in una nuova suddivisione, ridotta sempre di un quarto, e mantenendo l'orientamento come nel caso precedente.

 

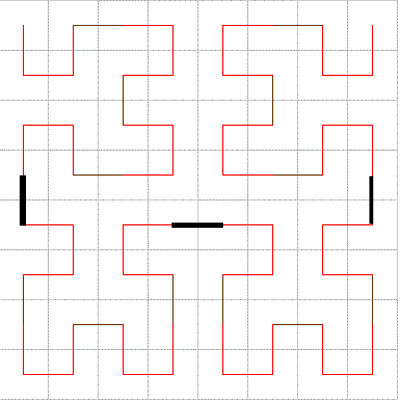
Al passo uno abbiamo 4 suddivisioni; al due  16 e al tre 64

se indichiamo con n il passo della costruzione, le suddivisioni sono  . , mentre la lunghezza del lato della suddivisione è ;la distanza di un punto qualsiasi del quadrato iniziale è minore o uguale a ; si intuisce che quando n va all'infinito, riusciamo a coprire tutto il quadrato. Per adesso abbiamo fatto solo una costruzione geometrica; di seguito definiremo una curva vera e propria,con funzione parametrica, e dimostreremo che è suriettiva.

 Curva parametrica  piana

una curva parametrica piana è una curva che giace interamente in un  piano ed è identificabile da una funzione continua da un intervallo di R in un sottoinsieme Q di  R x R

h:[a,b] ---->Q  R x R ; in pratica una funzione che associa ad un numero reale un punto nel piano R x R, t---->(x(t),y(t)); facciamo un esempio.

rappresenta una parabola.

Definizione della curva di Peano come curva parametrica

dividiamo il quadrato iniziale in quattro quadratini di lato 1/2 , che numeriamo con i numeri 1,2,34. L'ordine di numerazione è quello di percorrenza della prima curva approssimante:

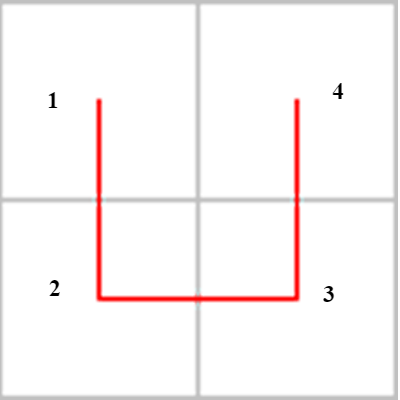
Dividiamo ora ciascuno dei quattro quadrati numerati  in altri quattro quadratini, ottenendo in tutto 16 quadratini (di lato 1/4)

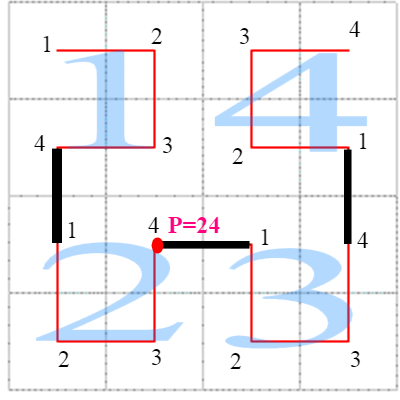
il punto P del disegno che appartiene al centro di un quadratino potrà essere individuato dalla dalla successione di numeri 24; 2 è il quadrato della prima suddivisione, 4 il quadratino della seconda suddivisione. Chiaramente questo è un caso semplice; il punto appartiene al centro di uno dei quadratini. Pensiamo al caso generale ; dato un punto qualsiasi appartenente al quadrato iniziale, come possiamo individuarlo con un procedimento iterativo? Ripetiamo la costruzione per ogni quadratino a cui il punto appartiene e la scriviamo ottenendo una successione di cifre (da 1 a 4).Il centro della successione di quadratini inscatolati convergerà al punto dopo infinite iterazioni. Il punto corrisponderà ad una successione infinita di cifre con valori compresi fra 1 e 4.

Avevamo promesso di dare una espressione parametrica per la curva di Peano Hilbert; cosa significa? Dobbiamo dare una funzione che associ ad un certo intervallo della retta una coppia di di valori nel piano, ovvero un punto del piano. Consideriamo l'intervallo [0,1];

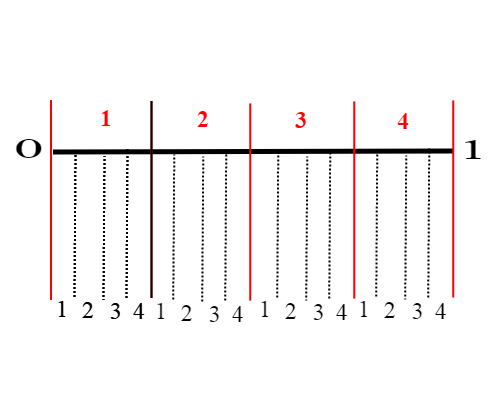
Suddividiamo l'intervallo in 4 parti, che numeriamo da 1 a 4 da sinistra verso destra; ciascuno di questi intervalli lo dividiamo ancora in quattro parti (e li numeriamo da 1 a 4 da sinistra verso destra;; iteriamo poi questo procedimento ai 16 intervalli generati,all' infinito. Dato un punto qualsiasi dell'intervallo [0,1], consideriamo la successione infinita di intervalli incapsulati che lo contengono; la successione di cifre che corrisponde agli intervalli si ottiene prendendo come prima cifra l'intervallo di ordine uno. seconda cifra l'intervallo di ordine due, e così via. Praticamente si procede così; data un punto p nel'intervallo [0,1] dividiamo l'intervallo in quattro parti; consideriamo l'intervallo che lo contiene (la sua posizione 1,2,3,4 ci dà la prima cifra della successione);  dividiamo l'intervallo trovato ancora in quattro parti e prendiamo ancora l'intervallo che lo contiene. Otteniamo una successione di intervalli incapsulati simile a quella che abbiamo visto QUI, che corrisponde anche ad una successione numerica(in genere) infinita di cifre che vanno da 1 a 4, ad esempio 23...

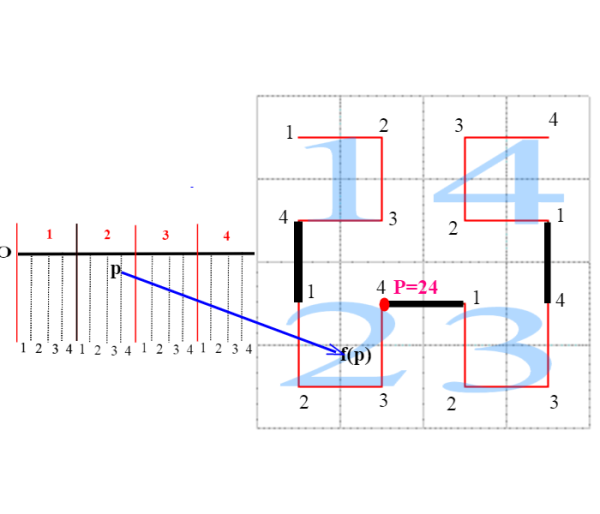
Il punto f(p) nel quadrato unitario è contenuto nei rispettivi quadrati 23...Viceversa, dato un qualsiasi punto del quadrato, esso sarà inscatolato in una successione di quadrati xyz.. il numero corrispondente nell'intervallo [0,1] lo troviamo negli intervalli corrispondenti a xyz.. dunque la funzione f (curva di Peano) è suriettiva.

Nell' articolo sull'assioma della scelta, abbiamo dimostrato che Se esiste una funzione f suriettiva f: B-->A, allora esiste una funzione iniettiva g di g: A-->B

Indichiamo con Q il quadrato unitario, e con I l'intervallo [0,1]. sappiamo che |I|<=|Q| (Immersione, ovvero I è contenuto in Q). essendo f:I-->Q suriettiva, esiste una funzione iniettiva di Q:--->I, ovvero |Q|<=|I|. Quindi Q|=|I|