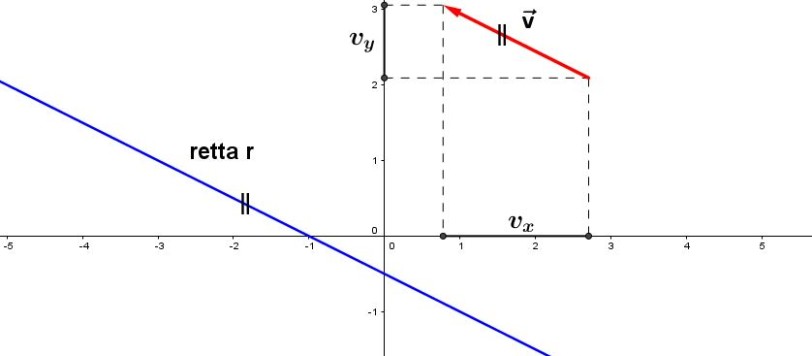
In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.