Fabricius e la pietra Lagrangiana - quinta parte

Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione.

Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.

Nelle puntate precedenti abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati (qui e qui) ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange (qui).

In questa quinta parte dell'articolo finalmente arriviamo alla equazione di Eulero-Lagrange. Ed ora...

..... squillino le trombe, rullino i tamburi,

ecco a voi l'equazione di Eulero-Lagrange!

$\dpi{200} \bg_white {\color{Red} \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot q}-\frac{\partial \mathfrak{L}}{\partial q}=0}$

C'è tutto il campionario delle derivate, ma ormai abbiamo imparato a conoscerle. Per esorcizzare ogni timore residuo vediamole una ad una ed applichiamole alla lagrangiana del pendolo che abbiamo trovato nella terza parte di questo articolo.

Il termine $\dpi{120} \bg_white \frac{\partial \mathfrak{L}}{\partial q}$ è la derivata rispetto alle variabili che abbiamo scelto come coordinate per descrivere il problema. Come spesso accade, ho chiamato genericamente q questa variabile. q può essere la w o la s della pista della slitta, la θ del pendolo o qualsiasi altra variabile che avessimo scelto di utilizzare. Questa è una caratteristica importante. L'equazione è sempre la stessa indipendentemente da tipo di coordinate, dalle cartesiane alle polari a qualsiasi altro tipo di coordinata che segua l'andamento del vincolo.

Ora applichiamo questa derivata alla lagrangiana del pendolo:

$\bg_white \large { { \mathfrak{L}=\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2 - m\, g\, r + m\, g\, r \cos({\color{Blue} \theta})}}$

In questo caso la nostra q è θ, quindi dobbiamo fare la derivata della lagrangiana rispetto a θ. Dobbiamo preoccuparci solo dei termini dove compare esplicitamente proprio θ , gli altri termini hanno derivata nulla. Questo è sostanzialmente quello che abbiamo visto ci dice di fare il simbolo ∂.

$\bg_white \large \begin{aligned} \frac {\partial \mathfrak{L}}{\partial \theta} & = \underbrace {\frac {\partial}{\partial \theta}(\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2)}_0 - \underbrace {\frac {\partial}{\partial \theta} ( m g r )}_0 +\underbrace {\frac {\partial}{\partial \theta}(m g r\, {\color{Blue} \cos(\theta)})}_{m g r{\color{Blue} (-\sin(\theta))}}\\\frac {\partial \mathfrak{L}}{\partial \theta}&= - m g r \sin(\theta) \end{aligned}$

Nel primo termine c'è $\boldsymbol{\dot \theta}$ che deve essere considerata come una variabile diversa da θ. Inizialmente questo mi ha confuso, ma ci si fa l'abitudine. Quindi la derivata del primo termine rispetto a θ è nulla. Tanto più la derivata del secondo termine dove θ non c'è proprio. Rimane il terzo termine. La derivata del coseno è il seno con il segno negativo (nel dubbio abbiamo sempre la scheda con le derivate più utili).

Il termine $\dpi{120} \bg_white \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot q}$ è la derivata rispetto al tempo di una derivata parziale rispetto a $\dpi{120} \bg_white \dot q$ .

Partiamo dalla derivata parziale. Sembra una cosa strana poiché è una derivata fatta rispetto ad una variabile che è esse stessa una derivata, ricordiamo che $\dpi{120} \bg_white \dot q$ è la derivata rispetto al tempo di q. Se però la consideriamo semplicemente come un'altra variabile, allora valgono le solite regole. Applichiamola ancora alla lagrangiana del pendolo:

$\dpi{120} \bg_white \begin{aligned} \frac {\partial \mathfrak{L}}{\partial \dot \theta} & = \underbrace {\frac {\partial}{\partial \dot \theta}(\frac{1}{2}\, m\, r^2 {\color{Blue} {\dot {\theta}}^2})}_{\frac{1}{2} m r^2 {\color{Blue} 2 \dot \theta}} - \underbrace {\frac {\partial}{\partial \dot \theta} ( m g r )}_0 +\underbrace {\frac {\partial}{\partial \dot \theta}(m g r cos(\theta))}_{0}\\\frac {\partial \mathfrak{L}}{\partial \dot \theta}&= m r^2 \dot \theta \end{aligned}$

Le derivate del secondo e terzo termine sono nulle perché non contengono $\dpi{120} \bg_white \dot \theta$ . La derivata del primo termine si ottiene dal solito prototipo già visto, $\dpi{100} \bg_white \frac{dx^n}{dx}=nx^{n-1}$

Ora occorre fare la derivata rispetto al tempo. Il simbolo d ci chiede di individuare non solo dove la variabile di derivazione t è esplicitamente presente, ma anche tutto ciò che può variare con il tempo. Applichiamolo ancora al pendolo:

$\dpi{120} \bg_white \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}=\frac{d}{dt}m r^2 \dot \theta=m r^2 \frac{d \dot \theta}{dt}=m r^2 \ddot \theta$

Qui il tempo non compare esplicitamente, ma $\dpi{120} \bg_white \dot \theta$ può variare nel tempo, cioè può essere una funzione non costante del tempo, $\dpi{120} \bg_white \dot \theta(t)$ . Invece m ed r nella lagrangiana del pendolo sono costanti. L'ultimo passaggio segue ancora la notazione di Newton che aggiunge un punto sopra la variabile per ogni derivata rispetto al tempo.

Ora rivediamo l'equazione di Eulero-Lagrange completa.

$\dpi{120} \bg_white \begin{aligned} \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}&-\frac{\partial \mathfrak{L}}{\partial \theta} =0 \\ m r^2 \ddot \theta &+mgrsin(\theta)=0\\ \ddot \theta =&- \frac {g}{r} sin(\theta) \ \textup{ equivalente a } \frac{d^2\theta}{dt^2}=- \frac {g}{r} sin(\theta) \end{aligned}$

Questa è l'equazione differenziale che descrive il moto. Per trovare come θ varia nel tempo, cioè la funzione θ(t), occorre risolvere questa equazione differenziale.

Ovviamente non è differente dalla equazione ottenuta con altri metodi, ad esempio analizzando la geometria del sistema ed applicando direttamente le equazioni di Newton. Non potrebbe essere differente altrimenti uno dei metodi sarebbe sbagliato. In effetti, alcune volte ciò che si ottiene appare differente, ma è solo una diversa forma della stessa espressione.

pendolo1

Qui ci siamo arrivati utilizzando il metodo di Lagrange e la lagrangiana attraverso alcuni passi che possiamo seguire in ogni altro problema. Ripercorriamoli per avere una visione d'insieme del metodo:

scelgo le coordinate: serve una sola coordinata per descrivere il moto ed abbiamo scelto l'angolo θ che segue la traiettoria di P
esprimo l'energia cinetica (K) nelle coordinate scelte: $\mathrm{la\, velocit\grave{a}\; di\; P\; \grave{e}}\; r\dot \theta \;\textrm{ quindi la sua l'energia cinetica sar} \mathrm{\grave{a}} \; K=\frac{1}{2} m (r\dot \theta )^2$
esprimo l'energia potenziale (U) nelle coordinate scelte: $U=mgh=mg\,r(1-\cos (\theta))$
inserisco K ed U nella espressione della lagrangiana:
$\dpi{120} \bg_white {\color{Blue} \mathfrak{L}=K-U}=\frac{1}{2} m (r\dot \theta )^2-\left (mg\,r-mg\,r\cos (\theta) \right )$
inserisco la lagrangiana nella equazione di Eulero-Lagrange:
$\dpi{120} \bg_white {\color{Blue} {\frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}-\frac{\partial \mathfrak{L}}{\partial \theta}=0}}$
$\dpi{120} \bg_white {{\frac{d}{dt}\frac{\partial}{\partial \dot \theta}\left ( \frac{1}{2} m (r\dot \theta )^2-mg\,r+mg\,r\cos (\theta) \right )-\frac{\partial}{\partial \theta}\left ( \frac{1}{2} m (r\dot \theta )^2-mg\,r+mg\,r\cos (\theta) \right )=0}}$
sviluppo le derivate ed ottengo l'equazione differenziale che governa il moto:

$\dpi{120} \bg_white \begin{aligned} &\frac{d}{dt}\left (m r^2 \dot \theta \right )-\frac{\partial \mathfrak{L}}{\partial \theta} =0 \\ &m r^2 \ddot \theta +mgrsin(\theta)=0\\ &\ddot \theta =- \frac {g}{r} sin(\theta) \end{aligned}$

Mi sembra che il metodo rispetti le intenzioni di Lagrange "Ridurre la teoria della meccanica … a delle formule generali, il cui semplice sviluppo fornisce tutte le equazioni necessarie per la risoluzione del problema" , "I metodi che espongo non richiedono né costruzioni geometriche né ragionamenti geometrici o meccanici, ma soltanto operazioni algebriche". Forse sul semplice potremmo non essere totalmente convinti, ma per il resto...

Per trovare esplicitamente come θ varia nel tempo, cioè la funzione θ(t), occorre risolvere l'equazione differenziale: $\dpi{120} \ddot \theta =- \frac {g}{r} sin(\theta)$ .

I matematici ci dicono che la soluzione esiste, ma non possiamo scriverla come una normale funzione. Quindi mi fermo qui citando Eulero (forse abusivamente in questo caso, ma suona bene) "Se non ci è permesso di penetrare fino ad una conoscenza completa del movimento non è alla meccanica e all'insufficienza dei principi conosciuti che bisogna attribuire la causa, ma è la stessa analisi che qui ci abbandona". Se lo diceva Eulero...

Ora abbiamo tutti gli elementi per tornare al punto di partenza. La frase di Enzo nell'articolo sui punti lagrangiani che mi aveva inizialmente incuriosito: "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana". Mi sono domandato cosa vorrà dire con più "fine". La prossima puntata vedremo la lagrangiana alla quale si riferiva Enzo cercando di capire cosa ci può essere di più "fine". Prima dovremo passare per un esempio di applicazione del metodo di Lagrange ad un sistema non inerziale che finora non abbiamo visto. Non ci devono essere sorprese perché il metodo di Lagrange è applicabile senza modifiche anche ai sistemi non inerziali. Anzi no, una sorpresina ci sarà, ma positiva...

Per chi volesse iniziare a ragionarci su, il sistema è un binario rotante orizzontalmente con velocità angolare costante ω. Dobbiamo trovare la lagrangiana di una massa vincolata a muoversi lungo il binario. La vista dall'alto è questa. La novità è che il riferimento del binario non è inerziale.

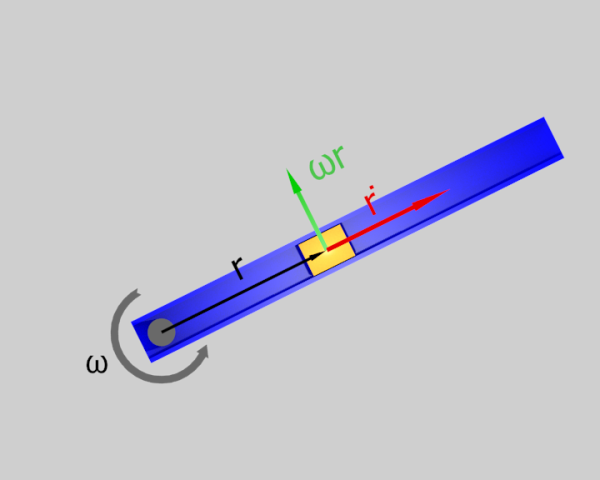
La procedura per trovare la lagrangiana è sempre la stessa con l'avvertenza che l'energia cinetica deve essere quella vista da un sistema inerziale come quello dal quale è presa l'immagine in figura.

La serie completa degli articoli sulla Lagrangiana la trovate QUI

L	M	M	G	V	S	D
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28

Fabricius e la pietra Lagrangiana - quinta parte

Articoli correlati

Un problema di ... conservazione ***

Due navi in mare aperto (*/**)

Sovrapposizione di stati: non solo gatti **

(Q) Velocità costante **/***

Lascia un commento Cancel Reply

(Q) Velocità costante /*