Categorie: Fenomeni astronomici Relatività
Tags: aberrazione della luce quiz relatività ristretta sistemi di riferimento soluzione
Scritto da: Vincenzo Zappalà
Commenti:2
Aberrazione della luce. 5bis: soluzione al quiz sull’orologio di luce **
Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.
Preferisco dare subito la soluzione o –meglio- l’interpretazione del QUIZ, che giudico la più corretta, Per non creare inutili confusioni. Capirete subito cosa intendevo mettere in luce.
Sì, lo ammetto, ho voluto fare il pignolo, anche se la soluzione datami è, in fondo, giusta… Tuttavia, vediamo di nuovo la Fig. 2 , mettendo i veri “nomi” ai vari “segmenti” e ricordando che la velocità della luce c è la stessa in qualsiasi sistema di riferimento.
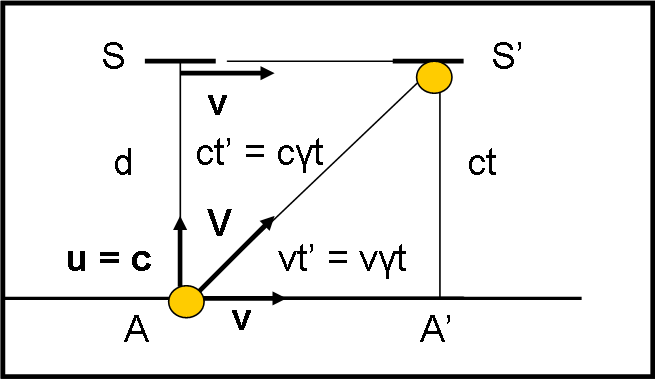
Il primo sistema di riferimento è quello di chi sta fuori e vede A e S muoversi verso destra con una certa velocità v. Il suo tempo sia t. Il secondo sistema di riferimento è quello del viaggiatore. Lui si considera fermo e per lui la luce emessa da A sale in S e torna nuovamente in A. Né A né S si sono mossi. Il suo tempo è ancora t (i tempi propri sono sempre uguali). Ne deriva che il percorso AS o A’S’ deve essere scritto come
d = c t
Così apparirebbe al viaggiatore e allo spettatore esterno se tutto fosse fermo. Come il viaggiatore si muove, il suo tempo proprio rimane lo stesso, ma non quello che osserva chi sta fuori e assiste alla scena. Per lui il viaggiatore ha un tempo t’.
Ne segue che:
AA’ = v t’
Analogamente:
AS’ = c t’
Sappiamo, però, molto bene che:
t’ = t γ
dove
γ = 1/( 1 – (v/c)2)1/2
Poniamo v/c = β
Imponendo c = 1, v = β.
Il fattore di Lorentz γ, si può scrivere:
γ = 1/( 1 – β 2)1/2
Nella Fig. 2 ad ogni t’, dobbiamo sostituire γt e quindi le varie lunghezze vengono riferite allo stesso sistema di riferimento e valgono:
AA’ = β γ t
A’S’ = t
Adesso possiamo uguagliare AA’ e A’S’ (i tempi sono gli stessi):
β γ t = t
β γ = 1
β = 1/γ
Ricordando il valore di γ, si ha
β = (1 - β 2)1/2
β2 = 1 - β 2
2β2 = 1
β = 1/√2
β = 0.7071
Non stupitevi se il risultato è lo stesso trovato in modo “brutale”. L’importante è avere capito il succo e sapere che cosa scrivere vicino ai vari segmenti, riferendoci sempre a un unico sistema di riferimento.
Ricordiamoci, infatti, che il viaggiatore vede sempre la luce rimbalzare verticalmente sullo specchietto, mentre è l’osservatore esterno che la vede descrivere una specie di zig-zag.
Dato che tutto avviene nello stesso intervallo di tempo t, possiamo anche considerare
t = 1
I segmenti diventano quelli riportati in Fig. 3. Questa ipotesi porta una descrizione che ci tornerà molto utile quando disegneremo l’ellisse di aberrazione, quella da utilizzare per sapere cosa e come si vede da un astronave che viaggia a grande velocità tra le stelle.
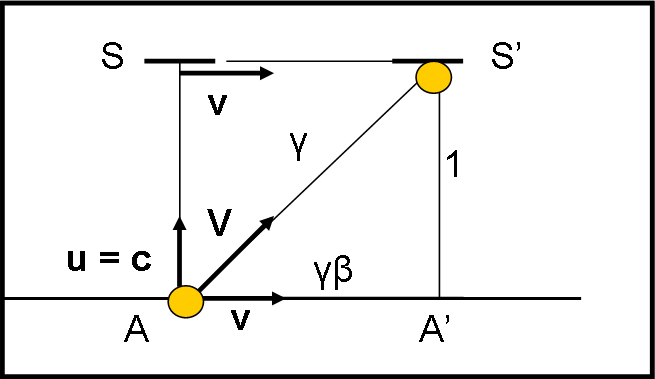
AS = A’S’ = 1
AA’ = γ β
A’S = γ
E tutto torna… nel nostro caso particolare, infatti:
AA’ = 1
A’S’ = 1
Da cui (con Pitagora):
1 + 1 = γ2
γ = √ 2
Scusate se ho, probabilmente, complicato qualcosa di apparentemente semplice. Tuttavia, le ragioni di questa specie di quiz era arrivare a due conclusioni:
1) Non legare mai lo spostamento apparente lungo l’asse delle x con la velocità v, per non correre il rischio di pensare che la visione di un triangolo AA’S isoscele voglia dire che si stia viaggiando si muove alla velocità della luce. Forse nessuno di voi avrebbe mai corso questo rischio, ma…
2) Ragionare solo in termini di β e γ, ponendo sia t che c uguali a 1 e v = β. Questa rappresentazione “sintetica” ci permetterà di lavorare meglio con l’ellisse di aberrazione, attraverso una figura come la Fig. 3.
Ecco un bel filmato riassuntivo, preparato dall'insostituibile Paolo!
Forse non si capisce ancora bene cosa c’entri l’aberrazione annua con questa famosa ellissi (poco spiegata nei pochi testi che la riportano e, quasi sempre, data per buona). Abbiate fiducia e tutti i vari pezzi convergeranno, un po’ alla volta.
La prossima volta torneremo dai nostri dei mitologici e come dignitari potremo considerare due Achille, dal piè veramente veloce! Faremo un nuovo quiz, ma questa volta senza creare confusione!







2 commenti
Caro Enzo, giusto per provare a chiarire meglio la differenza tra la fisica “classica” (ossia la relatività galileiana) e la relatività ristretta di Einstein ed anche per rispondere ad alcuni commenti apparsi qui (dato che ci sono problemi tecnici x visualizzare direttamente quell'articolo) vorrei provare a proporre un piccolo ragionamento.
Basandomi sull'animazione finale e prendendo come evento A la partenza della luce ed evento B il suo arrivo all'altro specchio verticale, è facile usando i diagrammi cartesiani provare a descrivere la situazione, secondo i due sistemi di riferimento, usando la fisica classica.
Per Galileo il tempo è assoluto, ossia è lo stesso per entrambi i sistemi di riferimento, mentre la velocità cambia: secondo il sistema considerato in movimento vi è solo una velocità verticale (Vy), mentre secondo il sistema fermo, la velocità V è la somma vettoriale tra la velocità verticale (Vy) e quella orizzontale (Vx) dovuta al movimento del treno (il modulo della velocità V si trova applicando il teorema di Pitagora).
Ovviamente, trattandosi di sistemi inerziali, nulla cambierebbe invertendo i sistemi di riferimento (ossia considerando fermo quello in movimento e viceversa e cambiando di posto all'orologio luce), a parte il verso della velocità.
Per Galileo non c'è alcun problema a sommare le velocità, senza alcun limite, peccato però che secondo il postulato di Einstein la velocità della luce è inviolabile ed è la stessa per qualunque sistema di riferimento (e tutto ciò è stato abbondantemente provato).
Pertanto se si prova ad usare la velocità della luce uguale per entrambi i sistemi di riferimento, tocca sostituire il valore di C (velocità della luce) sia a Vy che a V.
La relatività Galileiana con il suo tempo assoluto, entra in crisi a causa della costanza della velocità della luce che deve essere uguale per tutti i sistemi di riferimento, infatti applicando il teorema di Pitagora si ottiene un risultato impossibile!
Pertanto se la velocità della luce è un invariante, ossia è indipendente dal sistema di riferimento, ad essere relativi sono il tempo e lo spazio.
Infatti se tra l'evento A e quello B per il sistema in movimento passa 1 solo secondo (tempo t' misurato con un solo orologio), per quello considerato fermo (usando Vx=0,7 C) ne passa 1,40 (tempo t, misurato con più orologi sincronizzati tra loro), quindi per il sistema considerato fermo il tempo di quello considerato in movimento sembra scorrere più lentamente (dilatazione del tempo), come mostra la figura 3.
Spero che ora sia più chiara al differenza tra la fisica classica e quella relativistica!
Se ho detto qualche sciocchezza sono sicura che Enzo mi correggerà.
Paolo
Hai perfettamente ragione. Nel libro che ho scritto sulla RR ho sempre usato la pallina di luce nei diagrammi s-t. E' ovvio che se la velocità è sempre la stessa come modulo, quando vuoi raggiungere qualcosa che si allontana (per un sistema di riferimento) devi impiegare più tempo. Al limite, se lo specchio viaggiasse alla velocità della luce, la luce che parte da A non potrebbe mai arrivare in B e rimarrebbe sempre lungo l'asse del tempo (tempo infinito). Ci sono tanti modi per spiegare il ritardo e il fatto che la pallina di luce arrivi sullo specchio in diagonale, basterebbe dire che se un fenomeno capita in un sistema di riferimento deve capitare anche in qualsiasi altro. Se in quello in movimento la pallina tocca lo specchio, lo deve fare anche nel sistema fermo, a costo di viaggiare in diagonale!