Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica" (in Fisica Classica) e in  "Quattro passi nella storia della Scienza"

 

Che sia vera o meno la storia della mela che, dopo aver colpito la testa di Newton, lo avrebbe stimolato ad elaborare la sua Legge di Gravitazione Universale, resta il fatto che nel 1666 intuì che la legge fisica che fa cadere i gravi sulla Terra è la stessa che tiene in orbita la Luna.

Ma una cosa è avere un’intuizione, per quanto geniale, altra è riuscire a dimostrarla! E’ in questo passaggio che si manifesta tutto il genio di Newton il quale, partendo da leggi fisiche dimostrate da altri e grandezze fisiche misurate da altri, quindi usando “strumenti” già disponibili, li ha usati in un modo al quale altri grandi scienziati si sono avvicinati, senza tuttavia riuscire a raggiungere l’obiettivo che solo lui ha centrato. Vediamo come è riuscito a farlo…

Innanzitutto ipotizzò che il moto della Luna, considerato circolare in prima approssimazione, non fosse uniforme, ma procedesse “a scatti”, ovvero si componesse di due moti spezzettati nel tempo: uno rettilineo ed uniforme lungo la tangente ed uno, uniformemente accelerato, sulla direttrice del raggio a partire dal punto di arrivo del moto precedente.

Affinché il moto complessivo si sviluppi lungo una circonferenza, occorre che il segmento di caduta libera, dr, raggiunga la distanza media Terra-Luna dopo che quest’ultima si era allontanata di moto rettilineo ed uniforme lungo la tangente, come se l’effetto attrattivo della Terra non si fosse espresso.

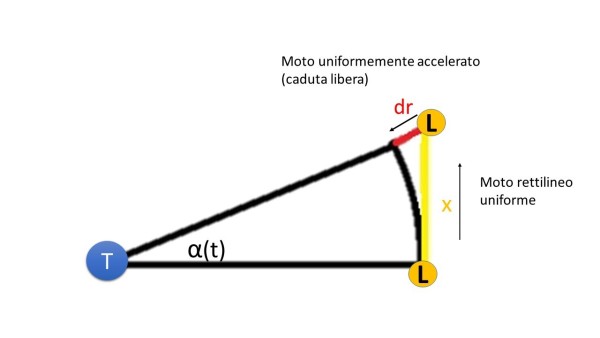
Quindi, se la sua intuizione fosse stata giusta, applicando le leggi del moto rettilineo uniforme e della caduta libera, avrebbe dovuto trovare dei valori coerenti con le osservazioni del moto lunare. E così fece.

Questi erano i DATI a sua disposizione:

Raggio della Terra = 6,5 x 10⁶ m

Distanza della Luna (media) = 380 x 10⁶ m

Periodo orbitale della Luna = 27 giorni x 24 x 60 x 60 = 2,33 x 10⁶ s

Accelerazione di gravità sulla superficie della Terra = 9,8 m/s²

Lunghezza dell’orbita lunare (Circonferenza) = 2 x π x Distanza della Luna = 2,39 x 10⁹ m

 

 

Calcoliamo il tragitto tangenziale (approssimato) percorso dalla Luna in un secondo:

X = Orbita lunare / Periodo orbitale lunare = 2,39 x 10⁹ m / 2,33 x 10⁶ s = 1,02 x 10³ m    (circa 1 km)

 

Calcoliamo adesso l’angolo al centro dell’orbita, supposta circolare, che la Luna percorre in un secondo:

α = 360° / periodo orbitale = 360° / 2,33 x 10⁶ s = 154,32 x 10^-6°/s  (circa 154,32 milionesimi di grado)

 

Dobbiamo ora calcolare lo spazio percorso dalla Luna, dr, dal punto finale del moto rettilineo uniforme fino a tornare sulla circonferenza che identifica l’orbita (quindi in un punto a distanza r dal centro della Terra). Questo tragitto viene percorso in caduta libera ovvero con moto uniformemente accelerato.

 

Dalla figura e dal teorema di Pitagora si ha che:

(r + dr)² = r² + 2 r dr + dr² = r² + r² tan²(α)

 

Trascurando il termine dr², la relazione si reduce a

r² + 2 r dr = r² + r² tan²(α)

 

Quindi dr = r/2 x tan²(α)    valida per dr molto piccoli

 

Sostituendo i valori:

dr = 380 x 10⁶m / 2 tan²(154,32 x 10^-6) = 1,37 x 10^-3m

 

Ossia, in un secondo la Luna percorre una distanza di circa 1 km e si abbassa verso la Terra di circa 1,4 mm. Il termine dr² è quindi trascurabile rispetto al raggio dell’orbita lunare.

Con questa informazione è possibile calcolare l’accelerazione alla quale è soggetta la Luna mediante la formula del moto uniformemente accelerato

 

dr = ½ a t²

 

da cui, noto dr, si ottiene

a = 2dr/t²

 

Quindi

a_L = 2,76 x 10^-3m/s²

 

Ora calcoliamo il rapporto tra l’accelerazione di gravità sulla superficie della Terra e alla distanza della Luna

a_T/a_L = 9,8 / 2,76 x 10^-3 = 3,55 x 10³

 

Il rapporto tra il quadrato del raggio dell’orbita lunare e il quadrato del raggio terrestre vale

r_OL²/r_T² = 3,42 x 10³

 

La differenza tra questi due rapporti è data dalle approssimazioni nei calcoli e dal fatto che ai tempi di Newton le stime del raggio terrestre e della distanza Terra-Luna non erano precise. Infatti è per questo motivo che preferì non pubblicare subito la Legge di Gravitazione Universale, ma lo fece solo molti anni dopo, quando, grazie a misurazioni più precise del raggio terrestre, si convinse che la forza di gravità diminuisce con l’inverso del quadrato della distanza, ovvero:

 

a_T/a_{L =} r_OL²/r_T²

 

e che tale formula non si limita a descrivere il moto della Luna intorno alla Terra, ma quello di ogni altro corpo nell’universo.

In sintesi, combinando i risultati degli studi di Galileo in merito al principio d’inerzia (un corpo persiste nel suo stato di quiete o moto uniforme finché una forza non interviene a modificarlo) e all’accelerazione gravitazionale, con la misura del raggio terrestre, della distanza Terra-Luna e della lunghezza dell’orbita lunare, riuscì a dare dimostrazione alla sua intuizione sulla vera natura del legame tra corpi, fossero essi sassi o pianeti o galassie, nonché a darne una quantificazione matematica.

Col senno di poi, sembra quasi banale ciò che ha fatto, ma se fosse stato così semplice, ci sarebbe arrivato prima di lui qualcuno degli altri grandi scienziati che si erano avvicinati molto al nocciolo della questione. Più di tutti si erano avvicinati Cristopher Wren, l'amico Edmond Halley e l'odiato Robert Hooke, ma nessuno di loro riuscì a conciliare la legge dell’inverso del quadrato della distanza con orbite ellittiche: tornava tutto, ma solo con teoriche orbite circolari e non ellittiche come erano in realtà… solo una mente geniale sarebbe riuscita a sciogliere quell’ultimo nodo!

P.S. Se siete perplessi perchè vi aspettavate di vedere la Legge di Gravitazione Universale nella forma che ci insegnano a scuola F=G(M₁M₂)/r² , sappiate che a tale formula si è arrivati solo molto tempo dopo. Newton , infatti, non riuscì mai a determinare il valore della sua costante gravitazionale G. Dovette quindi accontentarsi solo di rapporti di forze, in modo da eliminare quella scomoda costante, il cui valore fu ricavato solo un secolo e mezzo dopo grazie a sofisticatissimi strumenti di laboratorio e a piccole masse che, però, non servirono subito a determinare G, bensì la densità della Terra. Insomma, la storia di G è una lunga avventura nella quale il ruolo del protagonista è ricoperto dall'esperimento di Henry Cavendish del 1797-98 e ne parliamo QUI.

 

QUESTO il racconto dedicato a Isaac Newton a cui questa appendice si riferisce, QUESTO un approfondimento sulla ragnatela gravitazionale e i principi della dinamica e QUI trovate tutti gli altri racconti di Ciccio e Astericcio.

Nella rubrica dedicata alla Fisica di Papalla, invece, avete a disposizione una trattazione semplicissima del moto rettilineo uniforme e del moto uniformemente accelerato (QUI , QUI e QUI)

Mela o non mela… questo è il problema! QUI  una semplice e divertente spiegazione di Curiuss, coadiuvato dal fido assistente micio Gualtiero, sulla genialità dell’intuizione di Newton circa la Legge di Gravitazione Universale.

“Le lune e i pianeti sembravano dunque governati da una regola semplice e l’uomo l’aveva capita. Con questa regola l’uomo è stato in grado di prevedere il movimento dei pianeti e questa sarà la base del successo della Scienza negli anni a seguire, perché ha reso plausibile la speranza che altri fenomeni, nel mondo, siano governati da leggi semplici e meravigliose”. Questo ci dice Gatto Gualtiero (tradotto dal suo insostituibile collaboratore Alan) a proposito della Legge di Gravitazione Universale, in QUESTO VIDEO che di riduttivo ha solo il titolo… non perdetevelo!

 

Tutti i racconti di Ciccio e Astericcio sono disponibili nella rubrica ad essi dedicata