Categorie: Matematica
Tags: geometria Pappo di Alessandria quiz teorema di Pitagora
Scritto da: Vincenzo Zappalà
Commenti:24
QUIZ: Pappo è più bravo di Pitagora? **/*** (con soluzione)
Pappo di Alessandria (IV sec. d.C.) è stato sicuramente il massimo matematico del periodo ellenistico e alcuni suoi teoremi sono considerati la base per gli studi più moderni di geometria proiettiva. Tra le tante cose fatte, Pappo è riuscito a generalizzare il teorema di Pitagora, rendendolo solo un caso molto particolare. Vi propongo il problema come fosse un quiz (non particolarmente difficile). Ovviamente, anche se non è molto facile scovarla, la dimostrazione si può trovare nel web. Tuttavia, chi cerca di risolverlo in questo modo non ha capito niente del nostro Circolo e, quindi, spero che non abbia nemmeno il coraggio di pubblicare un copia-incolla, che sarebbe anche peggio di usare (male) Celestia…
Il teorema di Pitagora dice: la somma delle aree dei quadrati costruiti sui cateti di un triangolo rettangolo è uguale all’area del quadrato costruito sull’ipotenusa. Bene. Pappo fa molto di più e dice che: “ Dato un triangolo qualsiasi, la somma delle aree di due parallelogrammi qualsiasi costruiti su due lati è sempre uguale all’area di un parallelogramma costruito sul terzo lato.”
Fermo restando che il triangolo è qualsiasi e che i parallelogrammi costruiti sui due lati sono anch’essi qualsiasi (non hanno vincoli sul lato non appartenente al triangolo di partenza), costruire graficamente (nel modo più rapido possibile) il terzo parallelogramma che abbia area uguale alla somma delle aree dei primi due. Ovviamente è necessaria la dimostrazione…
Poi, potete divertirvi a far variare i parallelogrammi e a trovare il teorema di Pitagora. Se sarete bravi conosceremo anche altri teoremi di Pappo…
La SOLUZIONE più rapida (insieme a molte altre) l'ha data Maurizio nei suoi ultimi due commenti (si dice che sia stato aiutato da... Pautasso!), comunque la riportiamo SOTTO LO SPAZIO BIANCO. Certo è che i nostri maghi sono proprio bravi... possibile che nessuno cerchi di superarli?!
Questa soluzione si spiega con i colori....
Sui lati inclinati del triangolo ABC ci sono i due parallelogrammi GIALLI: AFGB e CDEB
Prolungo i lati FG e DE fino alla intersezione in H
Congiungo H con B, prolungando fino a intersecare I sul lato AC orizzontale e proseguendo oltre.
Su questo prolungamento riporto, dal Punto I, la distanza HB, individuando il punto L
Traccio la parallela a HL passante per A, individuando il punto P
Traccio la parallela a HL passante per C, individuando il punto O
I parallelogrammi ROSSI: APHB e COHB hanno aree rispettivamente uguali a AFGB e CDEB (basi e altezze uguali)
Prolungo anche i lati PA e OC . Sui loro prolungamenti riporto sia da A, sia da C, la distanza HB, individuando M e N
Traccio la congiungente MN
Il parallelogramma VERDE: AMNC è composto di due parti: AMLI e ILNC
Ma AMLI ha la stessa a rea di APHB e ILNC ha la stessa area di COHB (basi e altezza uguali)
Sul lato sinistro ho trasformato il parallelogramma GIALLO prima in quello ROSSO e poi in quello VERDE.
Lo stesso per il lato destro.
Alla fine i due parallelogrammi verdi accostati costituiscono un unico parallelogramma la cui area è la somma dei parallelogrammi gialli di origine.
Questa dovrebbe essere la dimostrazione più "classica" e forse la più "semplice" per il gioco intuitivo del doppio passaggio dei parallelogrammi ai loro equivalenti. Sicuramente la più "elegante" da un punto di vista geometrico.
Ma la maggiore semplicità/eleganza della dimostrazione non implica una maggiore velocità della costruzione grafica.
Intendo dire che il numero di linee da tracciare ( per la dimostrazione) è comunque il seguente:
2 prolungamenti di lati + 1 congiungente + 2 parallele passanti per un punto dato + 1 congiungente + 3 trasporti di una misura. In totale sono 9 gesti grafici contro i 7 della mia precedente dimostrazione in cui ho evitato deliberatamente il trasporto di misura (che credo sia consentito solo con il compasso).
Naturalmente la velocità della costruzione dipende anche dagli strumenti che stabiliamo "leciti". Ho ipotizzato riga(non graduata) e compasso. Ma se vengono ammesse anche le squadre (non graduate) per tracciare parallele e perpendicolari la "velocità" aumenta (per qualsiasi tipo di costruzione, ma in misura diversa secondo il mix di linee necessarie)
Passando da questa dimostrazione alla sua "pura costruzione grafica", i tre trasporti di misura si potrebbero ridurre ad uno solo ( IL=HB) ma, allora, la tracciatura della congiungente MN andrebbe sostituita con la costruzione di una retta parallela alla base passante per il punto L ,al fine di costruire il lato più basso del parallelogrammo verde.
Tuttavia, anche con questa semplificazione operativa, ritengo che questa costruzione non sia graficamente più veloce della mia precedente.
Naturalmente non escludo che esistano costruzioni grafiche ancora più "veloci" nella fase operativa, anche se potrebbero risultare più "complesse" nella loro fase dimostrativa.
Ma vediamo ora una ulteriore semplificazione e velocizzazione. La figura ora è questa:
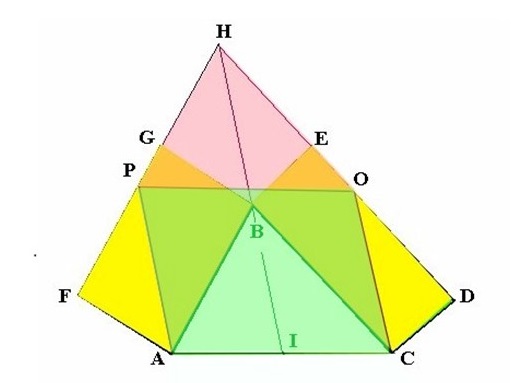
Senza rifare tutta la dimostrazione: invece di costruire il parallelogramma verde SOTTO il lato AC, lo costruisco SOPRA, dato che PA e OC sono entrambi uguali ad HB per costruzione.
Quindi basta collegare i punti P e O per avere il lato di chiusura del parallelogramma VERDE la cui area equivale alla somma dei due parallelogrammi GIALLI. ( già dimostrato)
In questo modo la costruzione si riduce a
2 prolungamenti (GH e EH)
+ 1 linea congiungente (HB I)
+ 2 parallele ad HB per i punti A e C)
+ 1 linea congiungente (PO)
In totale 6 tracciature.
Ovviamente i lati obliqui del parallelogramma VERDE possono essere inclinati a piacere purché restino paralleli tra loro, mantenendo la base AC e le intersezioni con la retta passante per PO
24 commenti
guardate che è piuttosto facile... perfetto per una domenica in casa ...
Mi ci stavo giusto applicando
Un dubbio: l'espressione "due parallelogrammi qualsiasi costruiti su due lati" è da intendere che ciascuno dei due parallelogrammi ha come lati i due lati del triangolo presi in considerazione ? Cioè, dato il triangolo qualsiasi ABC, il parallelogramma qualsiasi su AB ha come lati AB e BC, mentre il parallelogramma qualsiasi su BC ha come lati BC e AB ? In tal caso , il parallelogramma da costruire su AC avrà AC come base e come altezza un segmento da trovare graficamente in modo tale che la sua area sia uguale alla somma dei due parallelogrammi di cui sopra.
OK, quello che ho in mente funziona anche con parallelogrammi svincolati dal secondo dei due lati del triangolo presi in considerazione, che poi penso fosse il senso corretto della frase, come effettivamente precisato dopo nel testo del quiz. Aspetto un po' prima di proporre il metodo che avrei individuato (il condizionale è d'obbligo
)
I due parallelogrammi hanno ciascuno un lato che è uguale a un lato del triangolo. Il secondo lato dei parallelogrammi è qualsiasi e può essere diverso per i due parallelogrammi.
grazie per un po' di attesa prima della risposta....
Premetto che per ora non è mia intenzione dare una soluzione, ma la geometria in passato (ma pure adesso...) da me è stata davvero poco compresa...
Una cosa è imparare una formula che restituisce l'area di un parallelogramma, altro è capire il ragionamento che la sottintende.
Perciò, anche se tutto ciò apparirà a molti banale, ho realizzato una semplice figura che prova a mostrare perché l'area di un parallelogramma è uguale all'area di un rettangolo.
Sono convinto che ciò possa risultare utile per trovare la soluzione al problema posto... o perlomeno nella soluzione che ho elaborato, anche se non ho idea se sia la stessa fornita dal Dott. Pappo, sono partito proprio da questa constatazione...
Paolo
il nostro Paolo avanza sempre con molta logica e ho idea che abbia risolto il caso del Dott. Pappo in modo egregio... anche se non dico niete di più a riguardo...
Non saprei dire se Pappo è più bravo di Pitagora, comunque ha avuto 9 secoli di tempo in più per pensare.
Lasciamo ancora la notte e domani mattina ai lettori che si vogliono cimentare con la soluzione, prima di confrontare quelle che abbiamo in mente.
Lo so, non sono 9 secoli, però i tempi sono cambiati...
Probabilmente ci sarà una via grafica più veloce, ma io sono riuscito a trovare questa, che vi espongo.
L'area di un parallelogramma è data dal prodotto della base per l'altezza. Chiamo con a, b e c i lati del triangolo. Scelgo come lati su cui costruire i parallelogrammi qualsiasi i lati a e b. Chiamo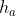
e 
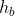le rispettive altezze dei due parallelogrammi. Chiamo, infine, con 
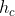l'altezza del parallelogramma da costruire sul terzo lato c. La condizione posta è esprimibile dalla relazione:
Una volta stabiliti i due parallelogrammi qualsiasi su a e su b, sono noti, graficament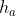e,
e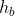 
. I lati a, b e c sono anche essi graficamente noti una volta dato il triangolo di partenza. Resta allora da determinare graficamente 
.
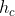Analiticamente questa incognita sarebbe subito data dalla suddetta relazione scritta come:
Si tratta allora di trovare un sistema grafico che operi come la suddetta equazione. Cioè, devo ottenere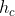
(altezza del parallelogramma su c) come somma di due segmenti, ciascuno dei quali è dato dal prodotto di segmenti. Il teorema di Talete si presta bene a questo scopo.
Allego ora la figura esplicativa in cui sono riportati il triangolo ABC di partenza, i due parallelogrammi qualsiasi su a e su b, uno dei parallelogrammi cercati su c e il procedimento grafico seguito.
Prolungo AC dalla parte di A di un segmento pari ad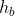
(basta prendere la misura con il compasso dell'altezza 
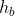e riportarla sempre con il compasso sul prolungamento di AC) e dalla parte di C di un segmento pari ad 
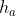(sempre con il compasso). Dai due punti terminali così ottenuti (indicati in figura rispettivamente con W ed S) mando le rette parallele rispettivamente al lato AB e al lato BC.
Prolungo ora il lato BC dalla parte di B e il lato AB dalla parte di B fino ad incontrare le due suddette rette nei punti rispettivamente indicati con Z ed U.
NOTA: la parte eseguente è analitica ma è da intendere come dimostrazione della parte grafica. Per questo motivo la scrivo con colore blu
Applico ora il teorema di Talete due volte. Una volta considerando le rette parallele BC e US tagliate dalle trasversali AU ed AS, e una volta considerando le rette parallele AB e WZ tagliate dalle trasversali WC (va bene, questa sigla è un puro caso :-) ) e ZC.
Nel primo caso si ha:
Nel secondo caso si ha:
NOTA: fine della parte dimostrativa analitica, riprendo il procedimento grafico.
Quindi, l'altezza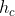
di uno dei parallelogrammi cercati sul lato c sarà data dalla somma dei segmenti BU e BZ, che ho indicato in figura, per evidenziarli, con il colore rosso e verde rispettivamente. Devo solo riportarli su una retta per A e perpendicolare al lato c. Mi servo ancora una volta del compasso e riporto prima la lunghezza di BU e poi, consecutivamente a questa, quella di ZB (ma posso invertire, il risultato non cambia). A questo punto ho la base (il lato c) e l'altezza (
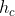) di uno degli infiniti parallelogrammi aventi area pari alla somma delle aree dei due parallelogrammi qualsiasi costruiti sugli altri due lati. Quindi posso disegnarne per esempio uno, quello che in figura ho colorato di ciano.
Ecco la mia descrizione della costruzione....
Triangolo ABC
Parallelogrammi gialli sui lati inclinati:
Parallelogramma sinistra...
base AC altezza AH angolo CAC' = alfa = angolo HAH'
AC' = AC cos(alfa) AH' = AH/cos(alfa)
Area parallelogramma = AC*AH = AC'*AH' (rettangolo AC'EH')
Parallelogramma destra...
base BC altezza BK angolo CBC' = beta = angolo KBK'
BC' = BC cos(beta) BK' = BK/cos(beta)
Area parallelogmma = BC*BK = BC'*BK' (rettangolo BC'DK')
La somma delle aree dei due rettangoli equivale all'area del rettangolo verde con base AB
e altezza C'F.
Determino il punto F in modo che l'area del rettangolo H'H''DE venga distribuita uniformemente al di sopra di H''K' (=AB)
Impongo quindi l'uguaglianza H''H'*H''D = DF*H''K'
da cui ricavo DF/H''D = H''H'/H''K' = K''K'/H''K' (triangoli simili)
Il punto cercato (F) è l' intersezione tra il lato comune ai due rettangoli C'E e la congiungente H''K''.
Ovviamente, invece del rettangolo verde, si può disegnare qualsiasi parallelogramma di base AB e altezza C'F.
Questa costruzione grafica con riga e compasso richiede il tracciamento di
3 rette perpendicolari alla base, passanti per un punto (A,B,C)
3 rette parallele alla base, passanti per un punto (H', K', F)
1 congiungente due punti, (H'', K'' )
senza alcun trasporto di misure.
Quanto al teorema di Pitagora resterebbe da dire...
“ dato che in un triangolo rettangolo la somma delle aree dei quadrati costruiti sui cateti equivale all'area del quadrato costruito sulla ipotenusa, anche la somma delle aree dei semicerchi costruiti sui cateti equivale all'area del semicerchio costruito sull'ipotenusa e non solo... per esempio: in questa figura la somma delle aree gialle equivale alla somma delle aree verdi."
Inoltre, a patto che il rapporto tra base e altezza dei rettangoli sia sempre il medesimo...
la somma delle aree di tutti i gigli di Francia sui cateti equivale all'area dei gigli sull'ipotenusa.
cari maghi,
siete stati veramente bravi, ma... la semplicità, a volte, è un pregio da valorizzare. Insomma, si puà ottenere il tutto molto più brevemente e facilmente... Aspetto qualcosa di meglio... Paolo aveva giustamente dato un'idea da tenere in conto...
Caro Enzo, per affrontare il problema, preferisco partire da una situazione particolare, in cui ho tracciato un triangolo, un rettangolo e tre particolari parallelogrammi costruiti sui lati del triangolo.
Graficamente è stato facile costruire il parallelogramma ABL'M' sul lato (AB) del triangolo, la cui area è la somma dei parallelogrammi costruiti sugli altri due lati del triangolo ABC.
Vediamo di arrivarci anche matematicamente, calcolando le varie Aree in gioco.
Area Parallelogramma (rosso) AFCE = (AF) h
Area Parallelogramma (blu) BHGC = (BH) h
Area Triangolo AFE = (AF) h/2
Area Triangolo ECA = (EC) h/2
Area Triangolo AIC = (AI) h/2
ma, nella figura, (AI) = (AF) = (EC) e l'altezza h è la stessa per tutti e tre, per cui i tre Triangoli e le loro aree sono uguali: (AF) h/2 = (EC) h/2 = (AI) h/2
Area Parallelogramma (rosso) AFCE = Area Triangolo AFE + Area Triangolo ECA
Area Parallelogramma (rosso) AFCE = (AF) h/2 + (EC) h/2
ma (AF) = (EC), quindi:
Area Parallelogramma (rosso) AFCE = AF h/2 + AF h/2 = 2AF h/2 = (AF) h
ma dato che (AF) = (AI) = (EC)
Area Parallelogramma (rosso) = (AF) h = (AI) h = (EC) h
Delle tre possibilità per determinare l'area, quella che risulterà utile, più avanti è:
Area Parallelogramma (rosso) = (AI) h
Area Triangolo BHG = (BH) h/2
Area Triangolo GCB = (GC) h/2
Area Triangolo BIC = (BI) h/2
Ovviamente si tratta di tre triangoli identici, così come le loro aree, dato che nella figura:
(BH) = (GC) = (BI)
Anche in questo caso, ovviamente:
Area Parallelogramma (blu) BHGC = Area Triangolo BHG + Area Triangolo GCB
Area Parallelogramma (blu) BHGC = (BH) h/2 + (GC) h/2
ma (BH) = (GC), quindi:
Area Parallelogramma (blu) BHGC = (BH) h/2 + BH h/2 = 2BH h/2 = (BH) h
ma (BH) = (BI) = (GC), quindi
Area Parallelogramma (blu) BHGC = (BH) h = (BI) h = (GC) h
Delle tre possibilità, quella che risulterà utile è:
Area Parallelogramma (blu) BHGC = (BI) h
Non resta che sommare le due aree trovate.
Somma delle due aree dei parallelogrammi= (AI) h + (BI) h = h (AI + BI)
ma (AI + BI) è la base (AB) sia del triangolo ABC, sia del rettangolo ABGE, per cui:
Somma area dei due parallelogrammi = (AB) h = base x altezza
proprio come l'area del parallelogrammo ABL'M' costruito sul lato AB avente altezza h!
A proposito di questa situazione particolare, ovviamente per costruzione la distanza tra H ed F è esattamente il doppio della base (AB).
Infatti:
(HF) = (FA) + (AI) + (BI) + (BH)
ma (FA) = (AI) e BH = (BI)
(HF) = (AI) + (AI) + (BI) + (BI) = 2(AI) +2 (BI) = 2 (AI + BI)
ma (AI+ BI) = (AB) = base
(HF) = 2 base
Questa, però è una situazione particolare e non generale.... infatti non vi è un vincolo per la lunghezza dei lati dei parallelogrammi.
Quindi, ho provato ad aumentare entrambi i lati dei due parallelogrammi iniziali rispettivamente di una certa quantità dXa e dXb, come mostra la figura.
Anche in questo caso meglio controllare le varie aree...
Area Parallelogramma (rosso) AXaYaC = (AXa) h
ma A Xa = (AF+FXa)
Area Parallelogramma (rosso) AXaYaC= ((AF)+(FXa)) h
Area Parallelogramma (rosso) AXaYaC = (AF) h + (FXa) h
Area Parallelogramma (blu) BxbYbC = (BXb) h
ma (BXb) = (BH + HXb)
Area Parallelogramma (blu) BxbYbC = ((BH) + (HXb)) h
Area Parallelogramma (blu) BxbYbC = (BH) h + (HXb) h
Somma Aree Parallelogrammi = (AF) h + (FXa) h+ (BH) h+ (HXb) h
Somma Aree Parallelogrammi = h (AF+BH) + h (FXa + HXb)
ma (AF) = (FI) e (BH) = (BI), per cui
(AF + BH) = (AI+BI) = (AB)
Somma Aree Parallelogrammi = h (AB) + h (FXa + HXb)
per semplicità definisco FXa come dXa e HXb come dXb
Somma Aree Parallelogrammi = h (AB) + h (dXa + dXb)
ma h (AB) non è altro che l'area trovata prima nella situazione “idilliaca”, per cui il parallelogramma da costruire sul lato AB per avere la stessa area della somma degli altri due parallelogrammi dovrà necessariamente modificare la sua altezza (la base deve per forza corrispondere al lato (AB) del triangolo ABC) per compensare l'incremento di area dovuto a: h(dXa+dXb).
Per trovare il valore dell'altezza h2 che dovrà avere il parallelogramma ABL''M'', parto dalla relazione:
Altezza parallelogramma = Area/ Base
h2 = (h (AB) + h (dXa + dXb))/(AB) = h + h (dXa + dXb)/(AB)
h2 = h (1+ (dXa + dXb)/AB)
h2 = h (1+ (dXa + dXb)/base)
h2 = (h base + h (dXa + dXb)/base
ma dXa + dXb = (Xb-Xa) - HF....
e HF = 2base
dXa+dXb = (Xb-Xa) -2base
h2 = (h base + h ((Xb-Xa) - 2 base))/base
h2 = (h base + h (Xb-Xa) - 2h base)/base
h2 = h base/base + h (Xb-Xa)/base -2h base/base
h2 = h + h (Xb-Xa)/base - 2h = h (Xb-Xa)/base - h
h2 = h ((Xb-Xa)/base – 1)
Ovviamente, nel caso iniziale dove (dXa + dXb) = 0, Xb coincideva con H e Xa con F, quindi in tal caso: HF = Xb-Xa = 2 base
h2 = h ((2base)/base – 1) = h ( 2-1) = h
Inoltre dXa e dXb possono anche essere sottratte invece che sommate alla iniziale situazione “idilliaca”, dato che la lunghezza dei lati dei due parallelogrammi può essere qualunque (e quindi anche più corta rispetto alla situazione di partenza) e se entrambi si sottraggono, si ottiene:
h2 = h (1- (dXa + dXb)/base)
da cui si arriva alla solita formula:
h2 = (h base – h (dXa + dXb)/base)
dXa + dXb = HF - (Xb-Xa) = 2 base - (Xb-Xa)
h2 = (h base – h (2base - (Xb-Xa))/base)
h2 = h base/base – 2h base/base + h (Xb-Xa)/base
h2 = h – 2h +h (Xb-Xa)/base = – h +h (Xb-Xa)/base
h2 = h (-1+ (Xb-Xa)/base)
h2 = h ((Xb-Xa)/base -1)
Ossia si arriva allo stesso risultato di prima, dato che tutto dipende dal rapporto (Xb-Xa)/base..
Se questo è uguale a 2 siamo nella situazione iniziale ((Xb-Xa) = 2 base), se è inferiore a 2 si sta sottraendo area alla situazione iniziale ((Xb-Xa) < 2 base), se è maggiore di 2 si sta aggiungendo area ((Xb-Xa) > 2 base)...
SEGUE
Finora, però, ho utilizzato come lati (liberi) del parallelogramma due segmenti orizzontali... ma i lati possono essere qualunque, quindi conviene vedere come usare quanto già trovato applicandolo nel caso che tali lati siano inclinati.
Nella figura, innanzitutto, parto da un lato del parallelogramma con inclinazione qualunque, per vedere come trovare il valore di Xa .
Nella figura è facile dimostrare che i triangoli YaCP e XaAS sono identici, comprese le loro aree..
I lati SA e PC del parallelogramma giallo hanno la stessa lunghezza e la stessa inclinazioni, dato che i due lati del parallelogramma devono essere congrui e paralleli...
Anche i lati PS e CA devono essere congrui ed hanno la medesima inclinazione...
Pertanto anche il segmento XaS è identico al segmento YaP ed i due triangoli sono identici...
D'altronde se tolgo l'area del triangolo YaCP (A1) dal parallelogramma giallo e la aggiungo sotto (A2 del triangolo XaAS), il parallelogramma blu non può che avere la medesima area di quello giallo:
Area Parallelogramma giallo = Area in comune + A1
Area Parallelogramma blu = Area in comune + A2.
ma A1 = A2
Area Parallelogramma giallo = Area Parallelogramma blu.
Una volta trovato il metodo, per ricavare Xa e Xb prolungando i lati dei parallelogrammi fino a raggiungere l'asse x, l'ho applicato ad un triangolo rettangolo, per arrivare al teorema di Pitagora.
A tal fine ho usato un triangolo rettangolo, inclinando i cateti del triangolo ABC di 45° questi tra loro formano un angolo di 90° ed il segmento AB (base) rappresenta l'ipotenusa del triangolo.
In questo caso avendo a che fare con triangoli identici, le basi dei tre triangoli in basso sono uguali, ossia:
XaA = AB = BXb = base
Basta sostituire nella formula generale ricavata prima, i valori di Xa e Xb ...
(Xb-Xa) = (XaA)+ (AB) + (Bxb)
ma (XaA) = (AB) = (BXb) = base
(Xb-Xa) = base + base + base = 3 base
Non resta che ricavare l'altezza h2 del parallelogramma costruito sull'ipotenusa AB
Altezza parallelogramma = h ((Xb-Xa)/base -1)
h2 = h (3base/base -1) = h (3-1) = 2h
Ovviamente, trattandosi di un quadrato (verde), il lato 2h (AM) è uguale al lato base (AB), per cui:
area quadrato verde = h2 base
ma h2 = base
area quadrato verde = base² = h2²
Quindi in questo caso:
Area parallelogramma rosso e quadrato giallo = (XaA) h = base h
Area parallelogramma blu e quadrato azzurro = (XbB) h = base h
Somma aree quadrati giallo e azzurro = base h + base h = base (h+h) = base 2h
Area quadrato verde = base h2
ma h2= 2h
Area quadrato verde = base 2h
Area quadrato verde = Somma aree quadrati giallo e azzurro
L'ho già fatta troppo lunga, per cui meglio fermarsi qui....
Paolo
un buon metodo Paolo... ma, si può fare più in fretta (direi)... parlo graficamente, ma la dimostrazione risulta ovvia per definizione di area di parallelogramma...
Questa soluzione si spiega con i colori....
Sui lati inclinati del triangolo ABC ci sono i due parallelogrammi GIALLI: AFGB e CDEB
Prolungo i lati FG e DE fino alla intersezione in H
Congiungo H con B, prolungando fino a intersecare I sul lato AC orizzontale e proseguendo oltre.
Su questo prolungamento riporto, dal Punto I, la distanza HB, individuando il punto L
Traccio la parallela a HL passante per A, individuando il punto P
Traccio la parallela a HL passante per C, individuando il punto O
I parallelogrammi ROSSI: APHB e COHB hanno aree rispettivamente uguali a AFGB e CDEB (basi e altezze uguali)
Prolungo anche i lati PA e OC . Sui loro prolungamenti riporto sia da A, sia da C, la distanza HB, individuando M e N
Traccio la congiungente MN
Il parallelogramma VERDE: AMNC è composto di due parti: AMLI e ILNC
Ma AMLI ha la stessa a rea di APHB e ILNC ha la stessa area di COHB (basi e altezza uguali)
Sul lato sinistro ho trasformato il parallelogramma GIALLO prima in quello ROSSO e poi in quello VERDE.
Lo stesso per il lato destro.
Alla fine i due parallelogrammi verdi accostati costituiscono un unico parallelogramma la cui area è la somma dei parallelogrammi gialli di origine.
Questa dovrebbe essere la dimostrazione più "classica" e forse la più "semplice" per il gioco intuitivo del doppio passaggio dei parallelogrammi ai loro equivalenti. Sicuramente la più "elegante" da un punto di vista geometrico.
Ma la maggiore semplicità/eleganza della dimostrazione non implica una maggiore velocità della costruzione grafica.
Intendo dire che il numero di linee da tracciare ( per la dimostrazione) è comunque il seguente:
2 prolungamenti di lati + 1 congiungente + 2 parallele passanti per un punto dato + 1 congiungente + 3 trasporti di una misura. In totale sono 9 gesti grafici contro i 7 della mia precedente dimostrazione in cui ho evitato deliberatamente il trasporto di misura (che credo sia consentito solo con il compasso).
Naturalmente la velocità della costruzione dipende anche dagli strumenti che stabiliamo "leciti". Ho ipotizzato riga(non graduata) e compasso. Ma se vengono ammesse anche le squadre(non graduate) per tracciare parallele e perpendicolari la "velocità" aumenta (per qualsiasi tipo di costruzione, ma in misura diversa secondo il mix di linee necessarie)
Passando da questa dimostrazione alla sua "pura costruzione grafica", i tre trasporti di misura si potrebbero ridurre ad uno solo ( IL=HB) ma, allora, la tracciatura della congiungente MN andrebbe sostituita con la costruzione di una retta parallela alla base passante per il punto L ,al fine di costruire il lato più basso del parallelogrammo verde.
Tuttavia, anche con questa semplificazione operativa, ritengo che questa costruzione non sia graficamente più veloce della mia precedente.
Naturalmente non escludo che esistano costruzioni grafiche ancora più "veloci" nella fase operativa, anche se potrebbero risultare più "complesse" nella loro fase dimostrativa.
Ho provato a ridurre tutto in due semplici figure e passaggi..
La prossima figura evidenzia come la relazione trovata valga anche per lati dei parallelogrammi inclinati (passatemi il termine), basta avere l'accortezza di ricavare i punti Xa e Xb prolungando i lati dei parallelogrammi fino ad incrociare l'asse x (la linea orizzontale su cui giace il lato AB del triangolo)..
...più beve di così...
Paolo
Ultima della notte....
Riprendo il mio ultimo post per una ulteriore semplificazione e velocizzazione. La figura ora è questa:
.
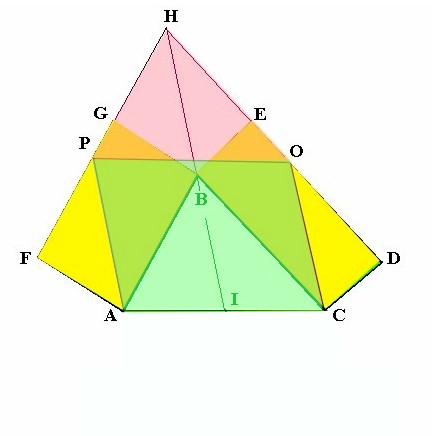
Senza rifare tutta la dimostrazione: invece di costruire il parallelogramma verde SOTTO il lato AC, lo costruisco SOPRA, dato che PA e OC sono entrambi uguali ad HB per costruzione.
Quindi basta collegare i punti P e O per avere il lato di chiusura del parallelogramma VERDE la cui area equivale alla somma dei due parallelogrammi GIALLI. ( già dimostrato)
In questo modo la costruzione si riduce a
2 prolungamenti (GH e EH)
+ 1 linea congiungente (HB I)
+ 2 parallele ad HB per i punti A e C)
+ 1 linea congiungente (PO)
In totale 6 tracciature.
Ovviamente i lati obliqui del parallelogramma VERDE possono essere inclinati a piacere purché restino paralleli tra loro, mantenendo la base AC e le intersezioni con la retta passante per PO
Visto che sono stato così “beve” da mangiarmi la erre... per fugare qualche dubbio sulla validità di trovare Xa ed Xb prolungando i lati dei parallelogrammi.. prendo in prestito la figura di Arturo, che però ho trattato solo ragionando per triangoli simili...
Anche in questo caso, più complesso, il metodo sembra funzionare!
Paolo
se Maurizio fosse un po' meno polemico e logorroico, sarebbe anche molto bravo (forse la colpa è del suo amico Pautasso che lo perseguita continuamente)
Comunque, il metodo da lui descritto (compasso o non compasso) è decisamente il più breve e immediato (almeno per me...) e il più comprensibile per chiunque...
La trasformazione verso Pitagora è altrettanto immediata.
Potete considerarla come soluzione ufficiale!!!!
Personalmente, dopo la pubblicazione del metodo grafico da me individuato, ero troppo curioso di confrontarlo con quello di Pappo di Alessandria. Così sono andato a vederlo, e questo mi ha squalificato per eventuali ulteriori commenti. Ora posso dire di riconoscere che il metodo di Pappo , che è sostanzialmente l'ultimo proposto da Maurizio, è decisamente più immediato e facile da dimostrare. Tra l'altro, se non ricordo male, la logica della dimostrazione è più o meno simile a quella che ricordo di avere trovato a suo tempo per il primo teorema di Euclide. Ora sarebbe bello trovare un metodo ancora più veloce. Ma penso che a suo tempo Pappo li abbia provati proprio tutti..
grande Arturo: l'essenza stessa del Circolo!!!!
Guardi, Professor Vincenzo, che io ho fatto di tutto per non fargli usare il compasso a quel maldestro, ma lui si è intestardito e alla fine, per fare la costruzione più veloce, si è anche punto con quegli aghetti acuminati, che a momenti mi toccava portarlo al pronto soccorso.
Comunque adesso si è calmato, dorme. Stia tranquillo che lo tengo d'occhio io.
Saluti ammirati , Oreste Pautasso
caro Oreste,
lei sì che è una persona riflessiva e anche rifrangente. Tra non molto, parlando di Napoleone, avrà pane per i suoi denti giustamente affilati sui "Ciciu" di Villar San Costanzo. Ah... Cuneo, che meraviglia!!!
Ossequi
enzo
Caro Professor Vincenzo, per i ciciu sono un po' preoccupato, perché anche se nella zona, i valori delle radiazioni gamma dovute al Cs-137, che rispecchiano le deposizioni al suolo dovute all'incidente nucleare di Chernobyl, sono nettamente inferiori ai livelli di guardia e di allerta, qualcosa di strano deve essere successo.
Basta guardare con un po' di attenzione queste due foto del 1985 e del 1987, prima e dopo il disastro.
Non si preoccupi, caro Oreste, i ciciu sono, in realtà, un particolare tipo di funghi pietrosi a lenta crescita... Anzi, dovesse andarci, me ne potrebbe procurare qualche quintale? Sono ottimi, soprattutto con le patate giganti!
suo
Vincenzo