Tempo fa, mentre facevo una passeggiata alla ricerca di un’ispirazione per un nuovo articoletto divulgativo da pubblicare nel nostro Circolo, la mia attenzione venne catturata da due ragazzini che stavano giocando a lanciarsi una pallina da tennis e da un distinto signore che li osservava con aria divertita e interessata… stavo per andarmene, quando mi accorsi che il signore stava usando un cronometro, quindi mi resi conto che in realtà quello non era un semplice gioco, ma un vero e proprio esperimento scientifico… potevo non fermarmi a curiosare?

I nostri amici Lorenzo e Riccardo stanno giocando con delle palline da tennis. Lorenzo è il lanciatore L, mentre Riccardo è il ricevitore R. La prima fase di gioco si svolge con i due amici fermi, mentre la seconda vede Riccardo allontanarsi da Lorenzo e la terza vede, invece, Riccardo avvicinarsi a Lorenzo. Il succo del gioco consiste nel prendere al volo cinque palline lanciate da Lorenzo, nei tre casi. Lorenzo le lancia sempre a ritmo costante, una ogni secondo. Un certo signor Oreste Pautasso assiste alla scena e si diverte a misurare il tempo che passa tra il lancio di Lorenzo e la presa delle palline da parte di Riccardo.

Inizia il gioco, con entrambi i ragazzini fermi. Lorenzo lancia le palline esattamente ogni secondo.

Il signor Pautasso misura e vede che Riccardo le afferra senza problemi. Ovviamente passa qualche secondo tra il lancio e la raccolta, ma a Pautasso interessa poco. Lui misura l’intervallo di tempo tra gli arrivi delle palline nelle mani di Riccardo. Il suo cronometro non può sbagliare e gli regala un risultato del tutto prevedibile: Riccardo ha ricevuto una pallina ogni secondo. Il gioco viene schematizzato nella Fig. 1.

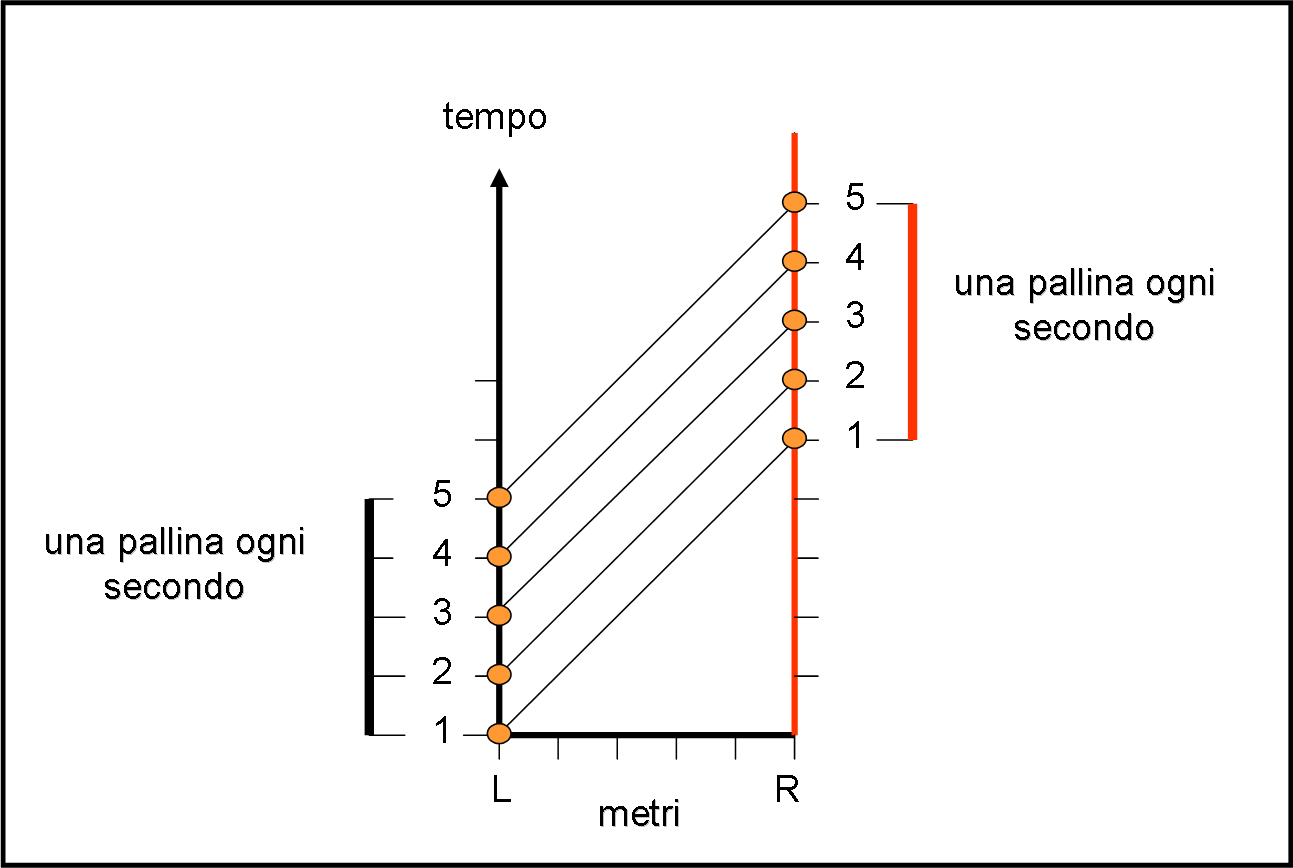
Nell’asse delle ascisse mettiamo lo spazio tra i due ragazzi L e R (anche questo ci interessa relativamente poco), mentre nell’asse delle ordinate, facciamo scorrere il tempo che passa nello stesso modo per tutti e due gli amici (non siamo in relatività ristretta!). Le palline vengono lanciate ogni secondo, si muovono in diagonale, ossia con una certa velocità, che vuol proprio dire muoversi di una certa distanza nell’unità di tempo, e vengono raccolte, dopo un certo tempo, da Riccardo. La figura mostra il risultato ottenuto con l’orologio di Pautasso: Riccardo riceve e afferra una pallina ogni secondo.

Passiamo adesso al gioco eseguito con Riccardo che si allontana da Lorenzo.

La Fig. 2 ci illustra molto bene quello che succede.

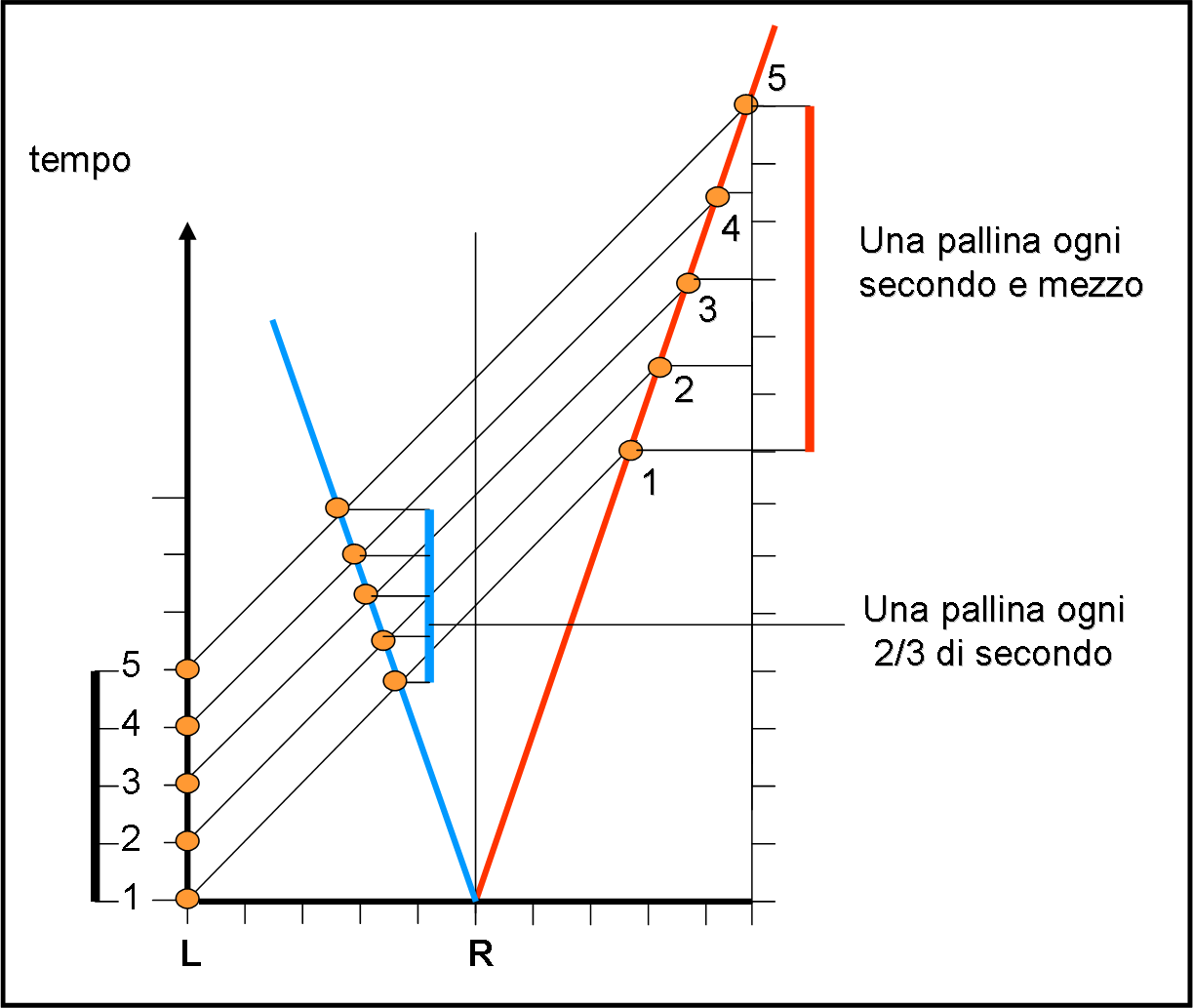
Riccardo si sta allontanando da Lorenzo con una certa velocità e quindi si sposta verso destra. Mentre corre riesce a raccogliere ugualmente le palline lanciate da Lorenzo ed è molto contento. L’allontanamento di Riccardo è mostrato dalla linea rossa. L’intersezione tra la linea che indica il movimento delle palline e la linea rossa (ossia Riccardo) ci regala gli istanti in cui le palline vengono ricevute.

Il signor Pautasso guarda il suo cronometro e teme che ci sia qualcosa che non va. E’sicuro che Lorenzo abbia continuato a lanciare le palline ogni secondo, ma Riccardo le ha ricevute a intervalli di tempo più lunghi, esattamente una ogni secondo e mezzo. Dà un’occhiata alla figura e pensa di capire il perché: ogni pallina impiega sempre più tempo (deve percorrere uno spazio più lungo) per raggiungere Riccardo e, quindi, è logico che il tempo che passa tra l’arrivo di una pallina e quella successiva sia aumentato in relazione alla velocità con cui Riccardo si è allontanato.

Non ci resta che invertire il movimento di Riccardo, che adesso è rappresentato dalla linea blu (sempre della fig.2)

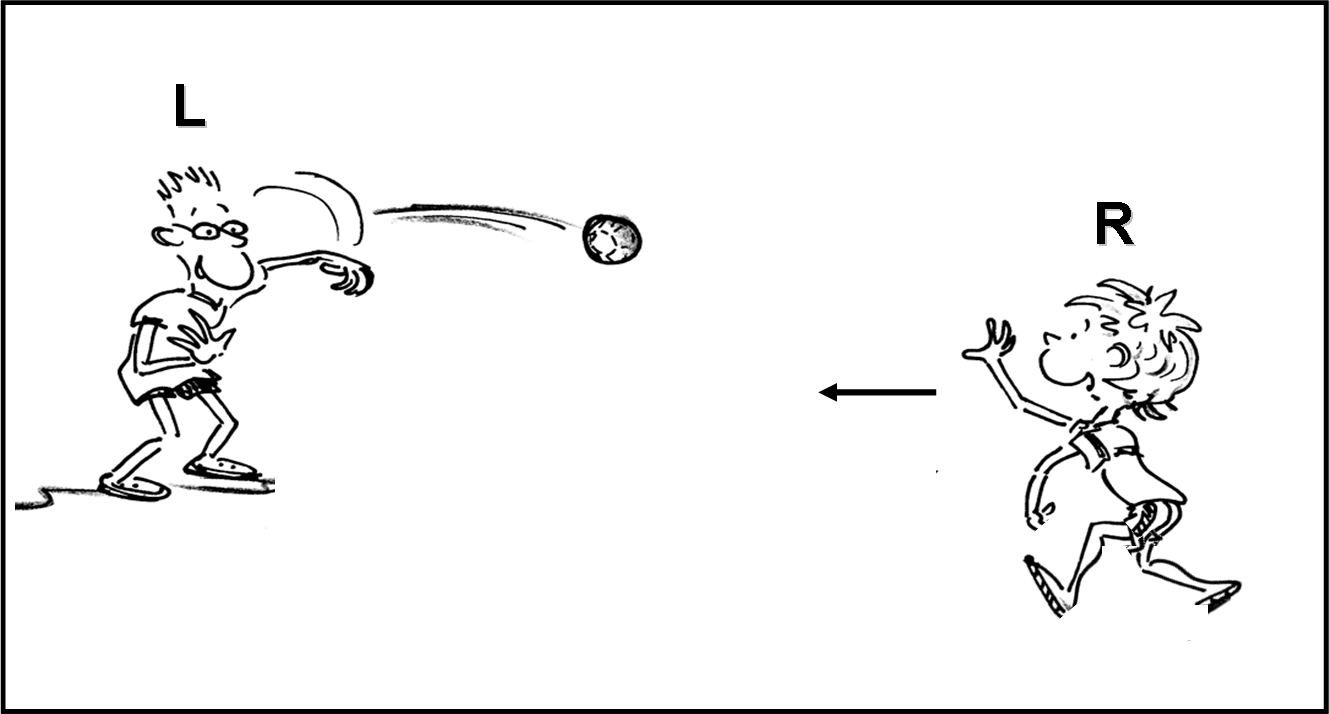
Lorenzo continua a lanciare le sue palline, una al secondo, mentre Riccardo gli corre incontro. Riccardo è molto bravo e riesce a prendere al volo tutte le palline e il signor Pautasso è costretto ad ammettere, di nuovo, che qualcosa sembra sbagliato. Il suo orologio si è messo a girare più lentamente? Questa volta, infatti, l’intervallo di tempo tra una pallina e l’altra , raccolte da Riccardo, è meno di un secondo, addirittura solo 0.75 secondi (3/4 di un secondo).

Un’attenta analisi della figura gli fa, però, tirare un sospiro di sollievo. E’ logico che le palline arrivino con maggiore rapidità, dato che adesso Riccardo si avvicina a Lorenzo e quindi il tempo che passa tra l’arrivo di una pallina e quella successiva deve diminuire, come diminuisce lo spazio tra i due ragazzi!

Sembrava, quindi, che tutto stesse procedendo per il meglio ma, dopo un breve colloquio con i ragazzi, il signor Pautasso sembrava terribilmente deluso… cosa era andato storto?

Rashomon (ovvero: il punto di vista del sig. Pautasso)

Gentile lettore,

dopo che mio cognato Mattia l’astronomo mi aveva raccontato di quel “misterioso” effetto Doppler che fa cambiare la voce delle sirene delle ambulanze (il suono è più stridulo se si avvicinano e più profondo se si allontanano) e che fa anche cambiare il colore delle cose che sembrano blu quando gli vai incontro e rosse quando invece le fuggi, mi sono proprio incuriosito ho voluto andare a fondo.

Così quando ho visto quei due “cit” che giocavano con la pallina da tennis mi sono detto: Pautasso, questa è la tua grande occasione di verificare l'attendibilità della fonte.

Ho spiegato a questo Riccardo che doveva prendere la pallina al volo, prima correndo in allontanamento e poi in avvicinamento, che poi gli avrei fatto io delle domande. Per non influenzarlo non gli ho detto niente dell'effetto Doppler!

Siccome c'era lì intorno un distinto signore con la faccia da professore che ci osservava compunto, per darmi un tono, ho tirato fuori il cronometro, come se volessi cronometrare questi lanci dei ragazzi, ma in verità a me interessava fino a un certo punto. Però ho notato questo fatto, che sembrava che le palline arrivassero con una frequenza maggiore quando Riccardo correva verso di loro e minore quando si allontanava, ma è una cosa normale, come quando piove che se uno corre incontro alla pioggia si bagna, mentre se scappa resta più asciutto, anche se la cosa più intelligente sarebbe trovare rifugio sotto un portone o, avendo la possibilità di spesa, entrare in un bar.

Così, per fare due parole con questo simpatico signore gli dicevo i secondi che misuravo tra una presa e l'altra. Mi è sembrato interessato anche perché ho visto che prendeva degli appunti.

Comunque a me interessava la questione dei colori. Così, dopo un bel numero di lanci, ho chiamato il Lorenzo e il Riccardo e gli ho fatto l'interrogatorio.

“Riccardo, questa pallina da tennis che vediamo è di colore giallo, ma che colore aveva quando la prendevi correndo verso Lorenzo? Era forse blu? E quando invece la afferravi al volo correndo lontano da Lorenzo era forse rossa?”

Il Riccardo mi ha lanciato un'occhiata sconsolata senza rispondere.

Allora ha parlato il Lorenzo…

“Eh, signor Pautasso, Riccardo è daltonico e dei colori non capisce niente...”

Ero così triste che l’esperimento fosse fallito...

Per fortuna, quel distinto signore con la faccia da professore mi ha tirato su di morale dandomi un po’ di spiegazioni… avrei potuto chiederle anche a mio cognato Mattia, che è astronomo (ma gli voglio bene lo stesso), ma lui era a portata di mano e mi sono accontentato.

Devo ammettere, tuttavia, che è stato talmente bravo da farmi capire che, anche se Riccardo non fosse stato daltonico, non avrebbe mai potuto vedere le palline che cambiano colore perché questo effetto doppler sui colori è percepibile solo a velocità molto alte, che solo le stelle possono raggiungere, non certo dei ragazzini che corrono in un prato.

Ora vi racconto cosa mi ha detto: per prima cosa ha tirato fuori un foglio di carta e qualche matita colorata (dice che le porta sempre in tasca perché non vuole usare programmini pappa-pronta… avrei voluto dirgli che se ce l’ha tanto con Masterchef, basta non guardarlo, e non capisco l’utilità di carta e matita… ma come può un umile raccoglitore di marroni in Cuneo contraddire un signore distinto con la faccia da professore?! Ho preferito annuire ossequiosamente…), quindi ha disegnato questa figura 3 e ha iniziato a spiegare…

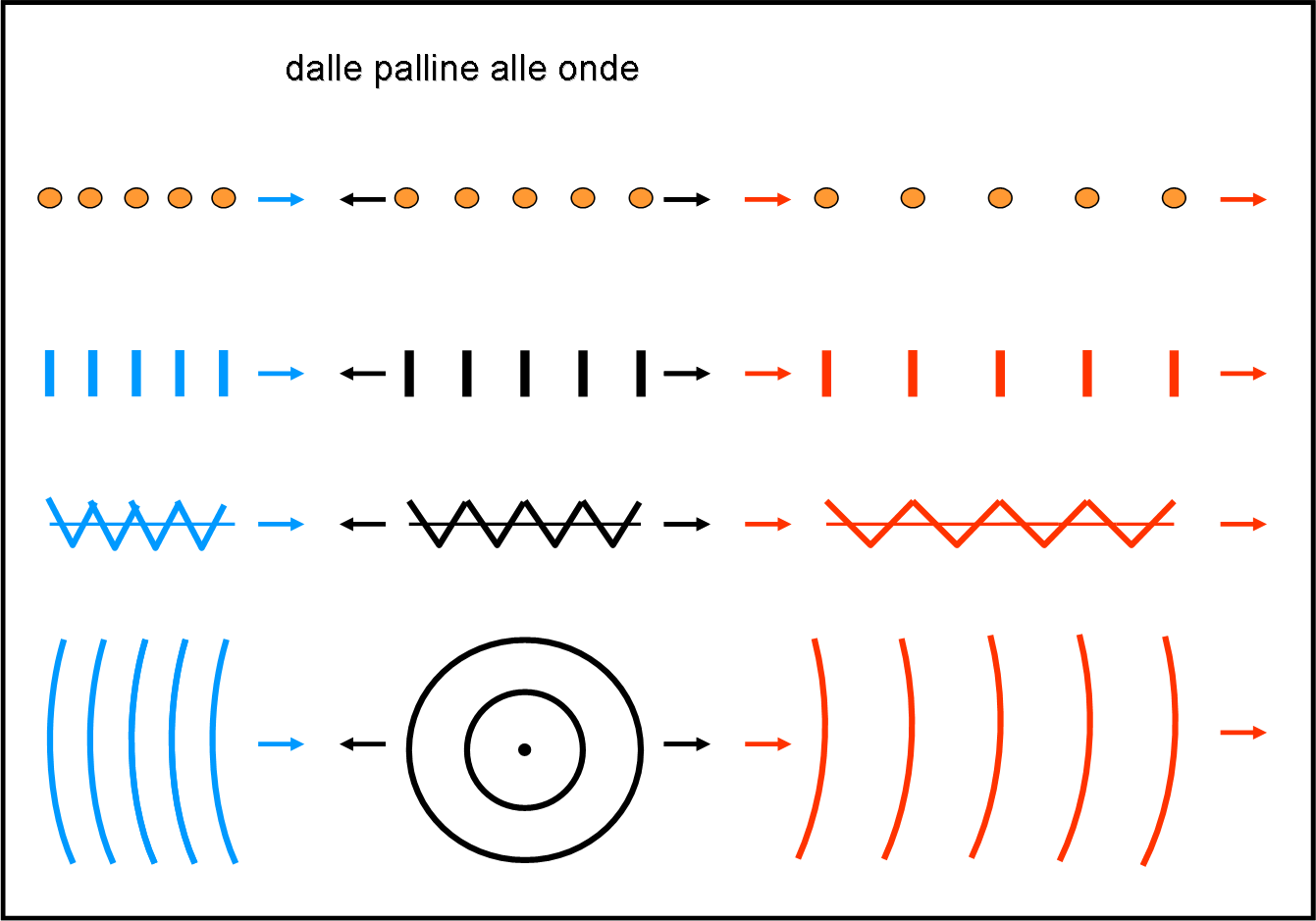
La riga in alto ripropone quanto successo con le palline. Al centro le palline lanciate che sono intervallate da un secondo. A sinistra le palline ricevute mentre Riccardo si avvicina, intervallate di 0.75 secondi; a destra le palline ricevute da Riccardo mentre si allontana, intervallate da un secondo e mezzo. Possiamo tradurre tutto ciò in parole un po’ più scientifiche. Il numero di palline lanciate o ricevute in un certo intervallo di tempo viene chiamata FREQUENZA. Maggiore è il numero di palline lanciate o ricevute in uno stesso intervallo di tempo e maggiore è la frequenza. Analogamente, se il numero diminuisce, la frequenza diminuisce.

Immaginiamo che le palline diventino sempre più piccole fino a diventare fotoni, ossia piccoli portatori di luce. Il discorso di prima ci dice che se Riccardo si allontana la frequenza di arrivo dei fotoni diminuisce, mentre se si avvicina la frequenza dei fotoni aumenta.

Al posto dei fotoni (che sappiamo comportarsi un po’ come particelle e un po’ come onde) possiamo mandare dei segnali qualsiasi (anche sonori) rappresentati dalle barrette della seconda riga. Nulla cambia rispetto a prima.

Immaginiamo, adesso, che i segnali non siano istantanei ma raggiungano un massimo, un minimo e di nuovo un massimo, in un certo intervallo di tempo, proprio quello corrispondente all’intervallo tra un picco e l’altro. Possiamo perciò disegnare la terza riga, che ci ricorda perfettamente le onde che si propagano, viste di lato. Abbiamo una cresta (punto più alto) e un ventre (punto più basso). La lunghezza dell’onda è proprio data dalla distanza tra una cresta e l’altra. Il numero di onde che arrivano in un certo intervallo di tempo è, allora, la frequenza. In poche parole, maggiore è la frequenza e minore è la lunghezza d’onda. Analogamente, minore è la frequenza e maggiore è la lunghezza d’onda. Questa constatazione si vede molto bene nella terza riga della figura confrontandola con quella precedente.

Possiamo, infine rappresentare le onde viste dall’alto e le palline o i segnali o le creste diventano le circonferenze che partono dal punto centrale. Quelle ricevute a sinistra sono compresse (minore lunghezza d’onda e maggiore frequenza); quelle ricevute a destra sono dilatate (maggiore lunghezza d’onda e minore frequenza).

Per concludere, possiamo immaginare le onde sia come onde acustiche, ma anche come onde luminose, ossia come quelle che rappresentano lo spettro elettromagnetico che, nel visibile, è legato ai colori (QUI una semplice spiegazione papalliana del fenomeno). Sappiamo molto bene che alle lunghezze d’onda più lunghe, nel visibile, corrisponde il rosso, mentre a quelle più corte corrisponde il blu (o meglio ancora il violetto). Ne segue che chi corre verso la sorgente della luce, supposta bianca, la vede colorarsi di blu, mentre chi corre in senso opposto la vede colorarsi di rosso

Ovviamente, la stessa cosa succederebbe se invece di muoversi chi raccoglie la luce (Riccardo) si muovesse chi emette la luce (Lorenzo).

Possiamo concludere che se una stella (sorgente di luce) si avvicina a noi la vediamo diventare più azzurra (blueshift- spostamento verso il blu), mentre se si allontana la vediamo diventare più rossa (redshift- spostamento verso il rosso). Una stella che va avanti e indietro rispetto a noi, in quanto orbita attorno a una compagna, deve mostrare, perciò, un colore che passa gradatamente dal blu al rosso e viceversa. Tra un picco blu e l’altro (o tra quelli rossi) è passato proprio il tempo necessario a completare un’orbita. Questo tipo di misura può dimostrare (anche senza vedere le due stelle separate) che esse formano una coppia e regala anche la misura del periodo di rivoluzione.

Quante informazioni racchiuse in questi piccolissimi fotoni che provengono dalle stelle!

QUI una spiegazione ultrasemplificata dell'effetto Doppler in perfetto stile "Astericcio"

QUI, invece, una spiegazione molto più seria dell'effetto doppler e di cosa lo differenzia dal redshift