Categorie: Matematica
Tags: doppia torta Pappo Pippo quiz soluzione
Scritto da: Club dei Maghi
Commenti:1
Soluzione del quiz sulla torta "virtuale" (seconda parte) ***
Cercando di collegare le tre soluzioni già date a al quiz sulla torta "virtuale", con diversi approcci, analitici e grafici, abbiamo trovato che ne esistono infinite. Così il risultato finale è una generalizzazione che porta ad un semplice metodo costruttivo delle soluzioni e mette in evidenza alcune particolarità grafiche che non potevano emergere se non avendo un quadro generale.
Le due soluzioni "intuitive" iniziali, trovate da Arturo (QUI e QUI), sono cerchi-base che, combinati linearmente, generano altri infiniti cerchi. Tutti hanno gli stessi punti di intersezione e i loro centri sono posizionati, per costruzione. sulla retta congiungente i due centri di questi cerchi-base. Tale retta è perpendicolare al segmento O1O2 che ha come estremi i centri dei cerchi-dati, quelli che rappresentano le torte del quiz.
Questa stessa particolarità è stata individuata anche nella terza soluzione, che vediamo nella figura seguente
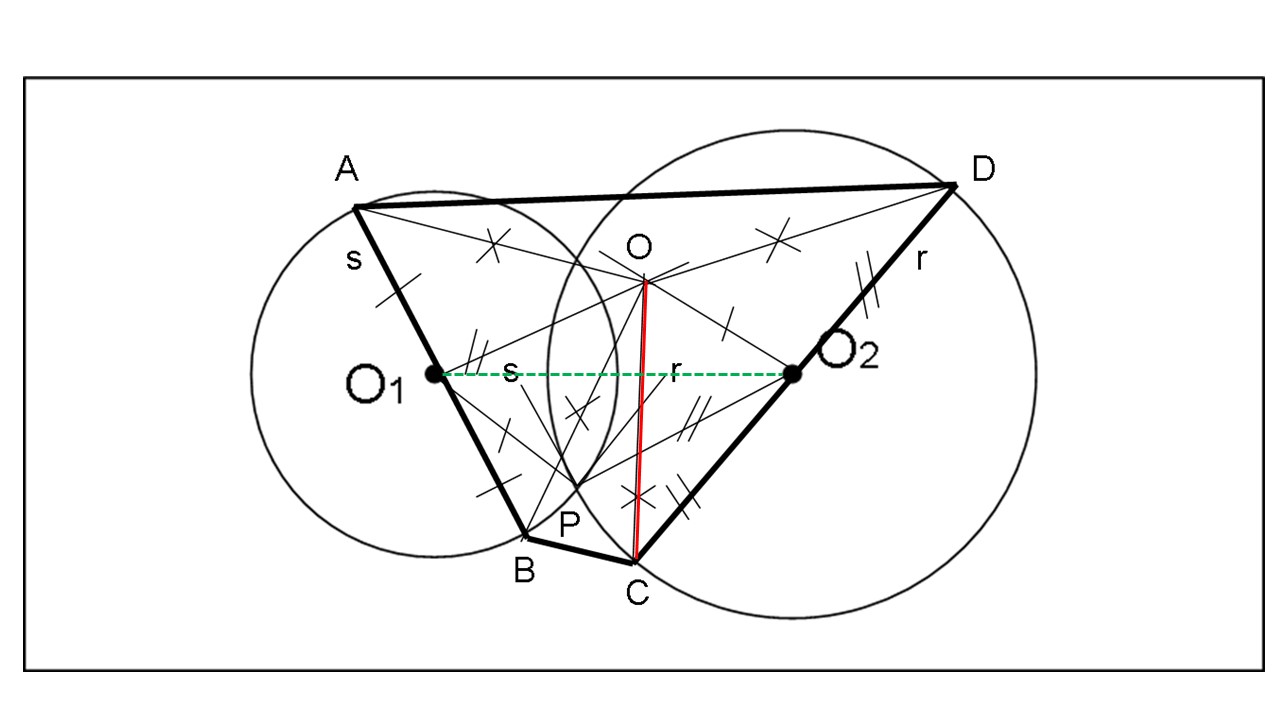
e che è stata spiegata QUI (da notare che la figura rappresenta un caso particolare in quanto la retta perpendicolare a O1O2 si sovrappone ad uno dei raggi della circonferenza).
E' su questo fascio di cerchi che vogliamo indagare per capire se quella retta, perpendicolare a O1O2, è il luogo dei punti equidistanti da ABCD, ovvero se esistono infinite circonferenze, che risolvono il quiz, il cui centro è situato su quella retta.
Vediamo come...
Vogliamo trovare i diametri, AB e CD, di due circonferenze i cui estremi possano essere congiunti da una terza circonferenza, la nostra "torta virtuale".
AB e CD non possono essere due diametri qualsiasi. Una circonferenza che passi per tre punti dati è sempre possibile trovarla, ma qui ne abbiamo quattro di punti.
Per dimostrarlo occorre solo il teorema di Pitagora. Vediamo come, osservando la figura sottostante, nella quale assumiamo che O sia il centro di una "torta virtuale". Il segmento q, evidenziato in rosso, è il nostro osservato speciale.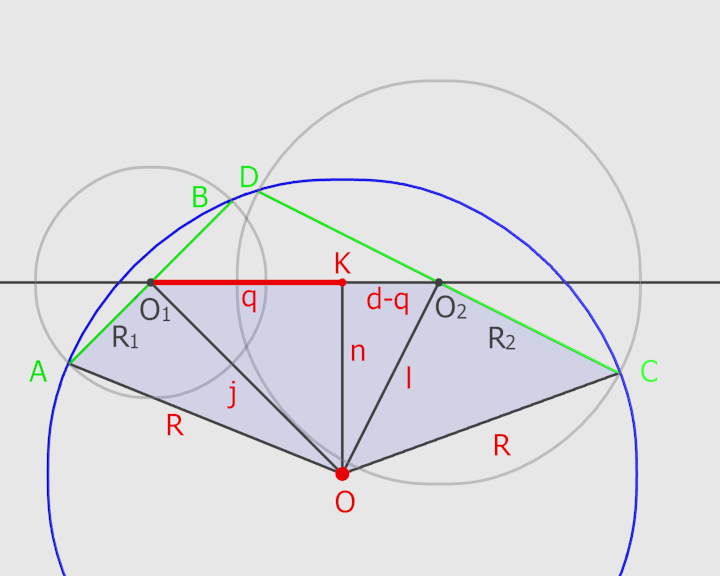
Nella figura ci sono quattro triangoli rettangoli posti a ventaglio: OAO1, OO1K, OKO2 e OO2C.
I due triangoli esterni sono rettangoli perché un raggio che taglia a metà una corda è perpendicolare alla corda. Se O è il centro di una "torta virtuale", allora AB e CD sono corde della "torta virtuale", e OO1 e OO2 le tagliano proprio a metà. I triangoli interni sono rettangoli perché li abbiamo disegnati noi così. K è proprio dove cade la perpendicolare all'asse O1O2 che passa per O.
Se O è il centro di una "torta virtuale", allora A e C si trovano alla stessa distanza da O. Indico con R questa distanza.
Applico il teorema di Pitagora a questi quattro triangoli.
dove
Queste espressioni sono fortemente legate tra loro poichè j ed l sono sia cateti dei triangoli esterni sia ipotenuse di quelli interni. Sfrutto questo fatto per trovare l'espressione di q.
Uguaglio la prima con la seconda che sono entrambe uguali al quadrato di R.
, quindi sostituisco j ed l con la loro espressione,
Elimino i termini comuni a destra e sinistra e risolvo in q.
dove nessuno dei termini a destra dipende dalla posizione di O.
Questo significa che q è uguale per tutte le possibili "torte virtuali". Questa caratteristica si vede bene in questa animazione che ha realizzato Arturo. O si muove su una retta perpendicolare a O1O2.
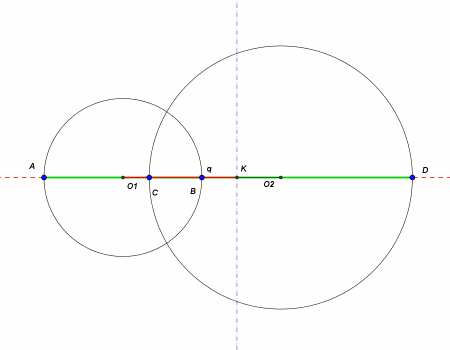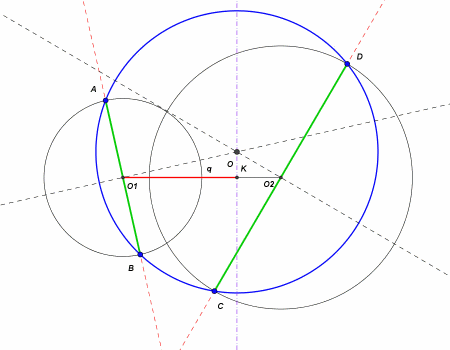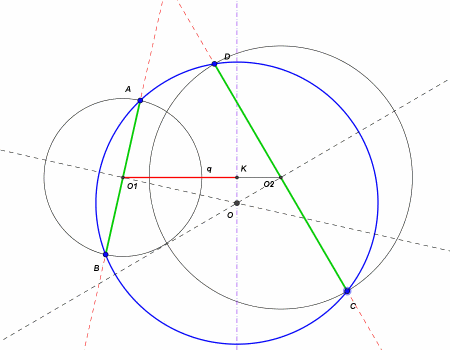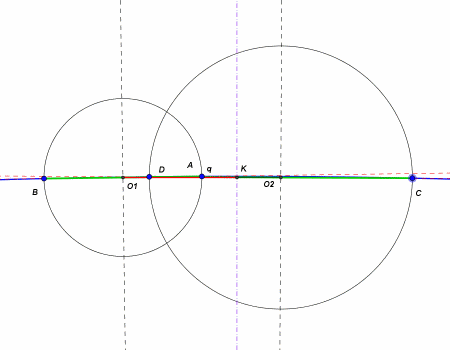
Ora che sappiamo per certo che i centri delle "torte virtuali" sono tutti allineati su un unica retta perpendicolare al segmento O1O2, possiamo proseguire più facilmente con la nostra ricerca.
La "torta virtuale" può essere trovata con un metodo grafico facendo uso di squadra e matita, come si vede più avanti (animazione 2). Volendo invece utilizzare un metodo analitico si può proseguire facendoci questa domanda.
Se prendo un diametro AB con una pendenza α qualsiasi, qual è la pendenza β del diametro CD che mi permette di tracciare una "torta virtuale"?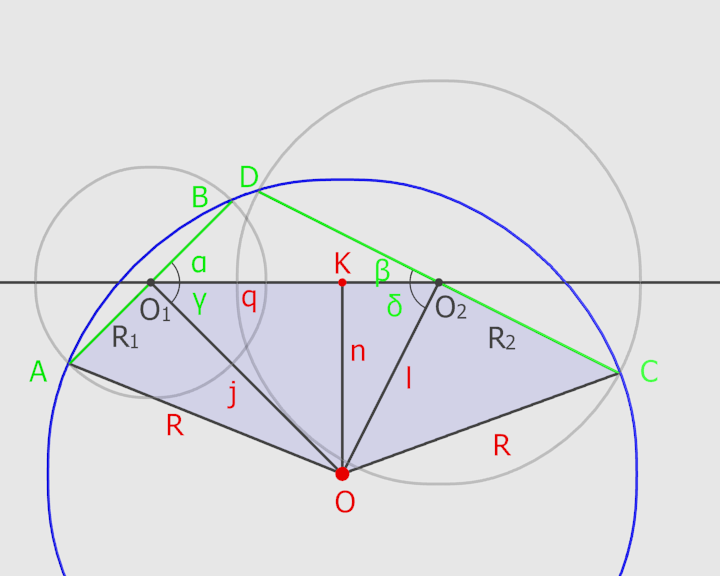
Poiché abbiamo visto che β non può essere un angolo qualsiasi, ci deve essere un legame con α che provo a trovare.
Sfrutto questa relazione trigonometrica:
Le tangenti dei due angoli sono proporzionali. Anche questo coefficiente di proporzionalità (d-q)/q dipende solo dalle due circonferenze iniziali e dalla loro distanza, quindi vale per tutte le "torte virtuali" indipendentemente dalla scelta di AB.
Applicando il teorema di Pitagora è possibile anche calcolare il raggio della "torta virtuale":
A questo punto abbiamo tutti gli elementi per un esempio numerico.
Se abbiamo due circonferenze di raggio R1=0,8 e R2=1,4 con centri distanti d=2, allora ed il rapporto
, che valgono per tutte le "torte virtuali" di questo caso.
Se scegliamo AB con una inclinazione α=30°, per la quale , allora
che corrisponde ad un angolo β≅16,22°.
La distanza del centro della "torta virtuale" dall'asse O1O2 sarà n≅2,3 ed il suo raggio sarà R≅7,7.
Una impostazione alternativa può essere questa...
Trovo inizialmente i centri della circonferenza che passa per ABCD nei due casi limite:
1: con assi dei diametri coincidenti 2: con assi paralleli
Ricordiamo che l'asse di un segmento è la perpendicolare al segmento nel suo punto medio.
Primo caso: assi coincidenti
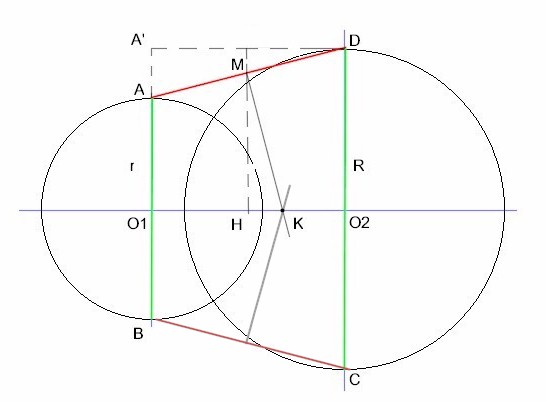
I due diametri sono verticali e paralleli. Il centro del cerchio che passa per ABCD si trova nel punto K, ottenuto intersecando l'asse del lato AD con gli assi di AB e CD. (il lato BC è simmetrico).
M è il punto medio di AD, H è il punto medio di O1O2.
I due triangoli rettangoli AA'D e KHM sono simili perché l'angolo compreso tra i segmenti A'D e AD è lo stesso compreso tra i rispettivi assi, quindi:
AA'/A'D = KH/HM
da cui KH = AA'*HM/A'D
AA' = differenza raggi = R-r ;
HM = media raggi =(R+r)/2
A'D = distanza tra i centri, che chiamo "d"
Quindi, in funzione di raggi e distanza tra i centri, posso scrivere
KH = (R-r)(R+r)/2d
Il punto K dista pertanto
da O1 e
da O2
Le distanze AK e DK sono uguali e, simmetricamente, lo sono anche BK e CK.
Risultato: ABCD sono sulla circonferenza di centro K
Secondo caso: assi paralleli
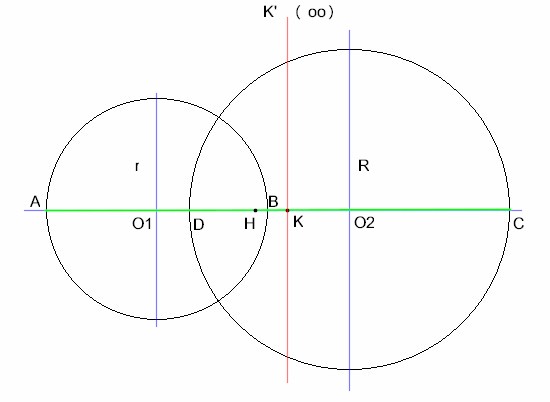 Ora i diametri sono orizzontali e si sovrappongono parzialmente nell'area di intersezione dei cerchi.
Ora i diametri sono orizzontali e si sovrappongono parzialmente nell'area di intersezione dei cerchi.
I rispettivi assi sono verticali e paralleli, quindi si intersecheranno in un punto all'infinito. Del resto i quattro punti ABCD sono allineati sulla congiungente O1O2 e la circonferenza di raggio infinito che passa per essi altro non è che questo asse orizzontale.
Il centro K' è quindi all'infinito e congiungerlo al centro K, trovato nel primo caso, significa semplicemente tracciare la verticale passante per K.
Considerazioni su un caso generico
Dimostreremo, facendo riferimento alla figura seguente, che tutti i punti della retta passante per i centri K e K' dei due casi limite, sono centri di circonferenze che passano per punti ABCD di diametri "coniugati"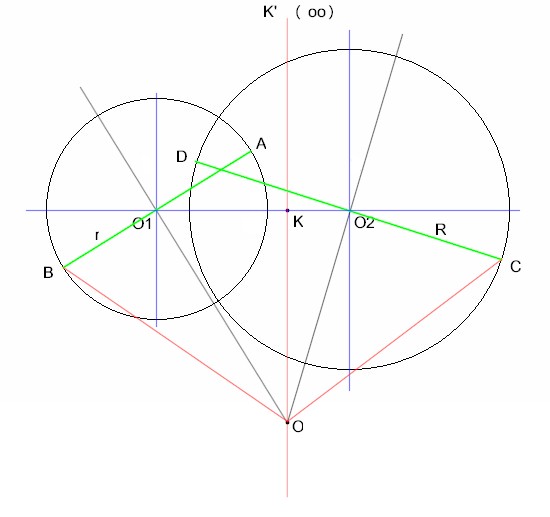
Scegliamo un punto O qualsiasi sulla retta per KK' e da O tracciamo le congiungenti con O1 e O2, che sono semplicemente gli assi dei diametri "coniugati". Quindi disegniamo i due diametri AB e CD, perpendicolari ai rispettivi assi. Possiamo unire O ai punti B e C, tralasciando di unire anche i punti A e D, dato che BOA e COD sono due triangoli isosceli e quindi OA=OB e OD=OC.
Indico con "x" la distanza di O da K ed esprimo OB ed OC in funzione di questa variabile "x", oltre che dei parametri fissi : raggi ( R ed r) e distanza di K dai centri O1 e O2 (che dipende dai raggi e dalla distanza tra i centri)
Applicando (due volte) Pitagora, esprimo i quadrati dei segmenti OB e OC come segue:
A questo punto, eseguendo la sottrazione tra queste due espressioni, notiamo che la dipendenza da x scompare. Questo significa che i segmenti OB e OC differiscono tra loro per una costante, legata ai parametri costruttivi: raggi e distanza tra i centri. Questa constatazione implica che è sufficiente conoscere il valore della costante (ad esempio in un caso limite) per poterla estendere a tutti i casi. Naturalmente nei casi limite la differenza tra i segmenti OB e OC è nulla, quindi lo sarà anche in ogni altro caso.
Concludendo OB=OC
e ciò implica uguali distanze per tutti i punti ABCD da O.
Valore del raggio della circonferenza passante per ABCD e centro in O
Un volta scelta la distanza KO (=x), che determina la collocazione del centro O, il calcolo del raggio, utilizzando le precedenti espressioni di OB (oppure OC), conduce in pochi passaggi, al seguente risultato.
Raggio = √ { (d/2)2 + [( R2- r2)/2d]2 + (R2+r2)/2 + x2 }
Al piccolo Pappo non resta che seguire queste istruzioni e trovare tutte le soluzioni gli servono.
Costruire la retta KK' con l'uso di una squadretta per tracciare l'asse che individua K e per disegnare la verticale passante per K. Tutti i punti di questa retta verticale sono valide soluzioni. Si sceglie O, si tracciano OO1 e OO2 e poi, perpendicolarmente con la squadretta, i relativi diametri "coniugati" , avendo la certezza che per i quattro punti ABCD passa sempre una circonferenza con centro in O.
Questa animazione, messa a punto da Fabrizio, illustra efficacemente i vari passi.
Osservazione : Tutte le le circonferenze passanti per punti ABCD hanno un punto in comune
Dimostrazione
La precedente espressione OB2 = O1B2 + OO12 = r2 + x2 + KO12 = x2 + KO12+ r2
può essere riscritta sinteticamente in questo modo: Raggio2 = x2 + Costante2
Il caso di x=0 corrisponde ad avere il centro O nel punto K.
Osservando la prima figura, a cui abbiamo aggiunto il disco della soluzione e la retta verticale per il punto K vediamo che avendo posto x=0, il raggio AK altro non è che la “Costante”.
(nel triangolo rettangolo KAO1 la somma dei quadrati di KO1 e O1A è il quadrato dell'ipotenusa AK. Si noti che O1A non è altro che il raggio r del cerchio di centro O1)
Se riporto AK lungo la retta orizzontale che passa per O1O2 trovo un punto Z. (ZK=AK)
Scelto un qualsiasi punto O sulla verticale KK', a distanza x da K, posso constatare facilmente che il raggio OZ è l'ipotenusa del triangolo rettangolo che ha cateti ZK e KO.
(per Pitagora OZ2=OK2+ZK2 ossia Raggio2 = x2 + Costante2 )
Questo vale per qualsiasi scelta di O, quindi tutte le circonferenze passano per Z.
In sintesi, trovato Z nel modo descritto posso scegliere O e tracciare subito la circonferenza passante per Z ottenendo la soluzione.
Naturalmente, per la simmetria della costruzione, esiste un punto Z' diametralmente opposto a Z con le stesse caratteristiche. Insomma, Z e Z' sono i punti di intersezione di infiniti cerchi-soluzione e sono i punti per cui passa l'asse radicale di questo fascio di circonferenze.
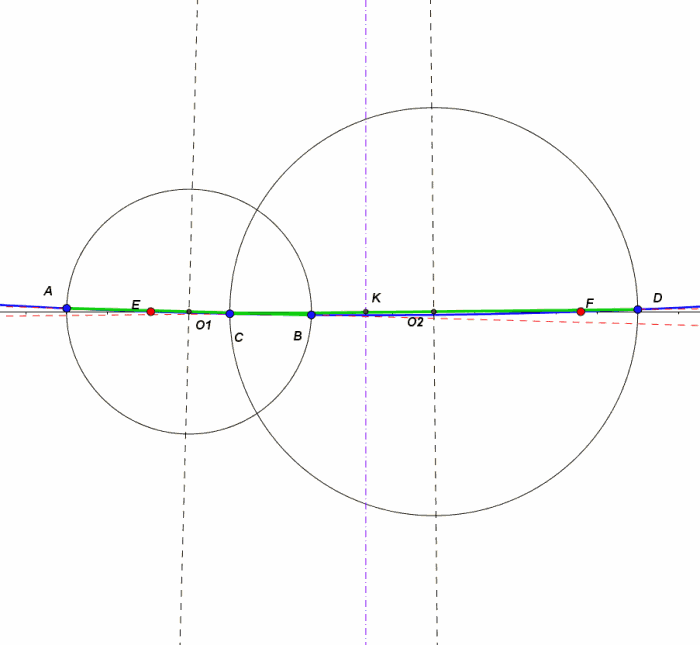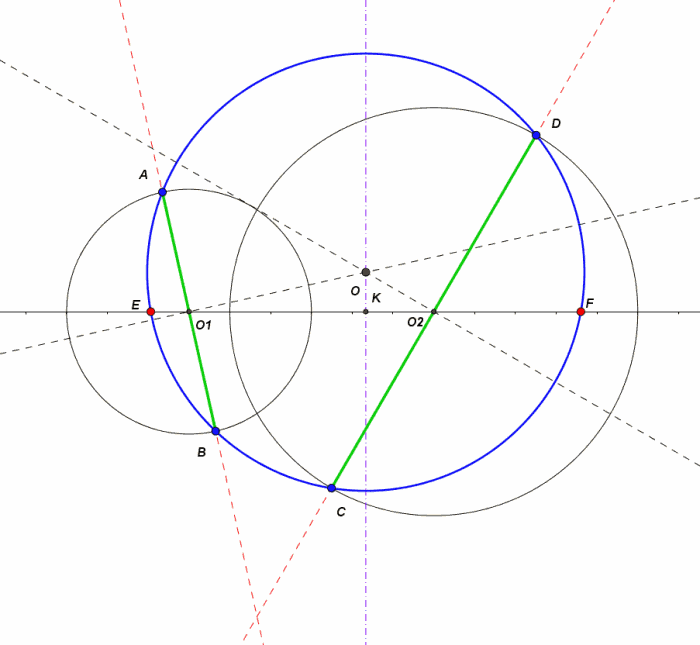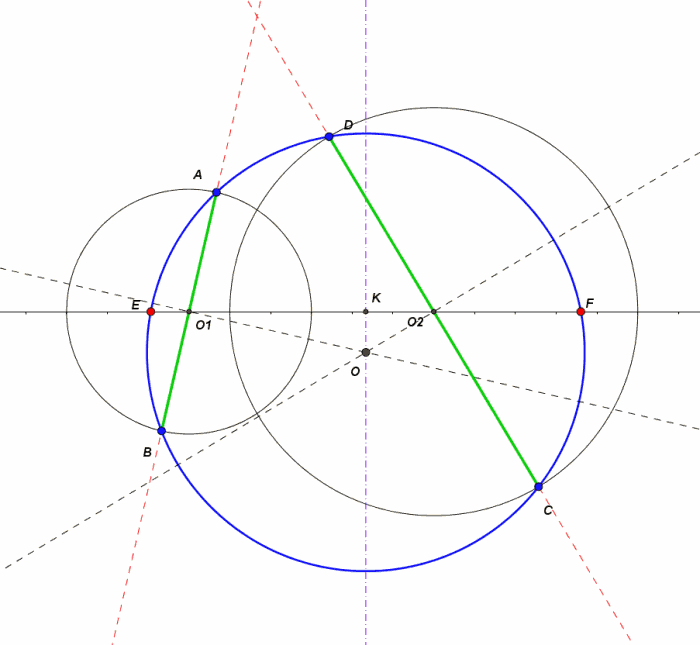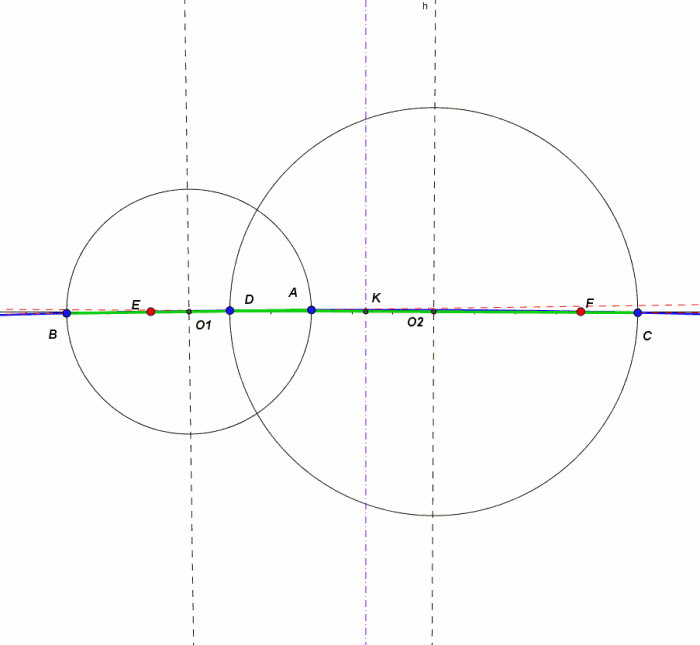
Grazie a questa bella animazione, predisposta da Arturo, la particolarità questi due punti ( qui chiamati E ed F ) non può sfuggire all'osservazione.
QUI potete trovare molti altri quiz








1 commento
Attraverso un semplice quiz, siete riusciti a creare un corso di geometria... Siete fantastici!!!! Direi, perfino, che è leggibile come una vera opera d'arte. Concludo, dicendo che quando si capiscono le cose, l'aiuto della tecnica grafica può essere fondamentale e di grande spettacolarità. Ma, ripeto, PRIMA si deve capire bene ciò di cui si parla...
Grazie maghi... siete proprio dei maghi!!!!