Quiz: Una torta e due triangoli *** (con aggiunta)
Oggi è il diciottesimo compleanno di Pappo (quanto tempo è passato), ma Pippo non è cambiato e si diverte a mettere in difficoltà il fratello, anche se con sempre maggiore difficoltà: a furia di tagliare torte in modo strano, Pappo è diventato un piccolo mago della geometria. Pippo deve dare il meglio di sé…
Nel pomeriggio, prima della festa, Pippo fa uno strano disegno, attorno a un cerchio di raggio r qualsiasi che simula la torta, mostrato in Fig. 1.
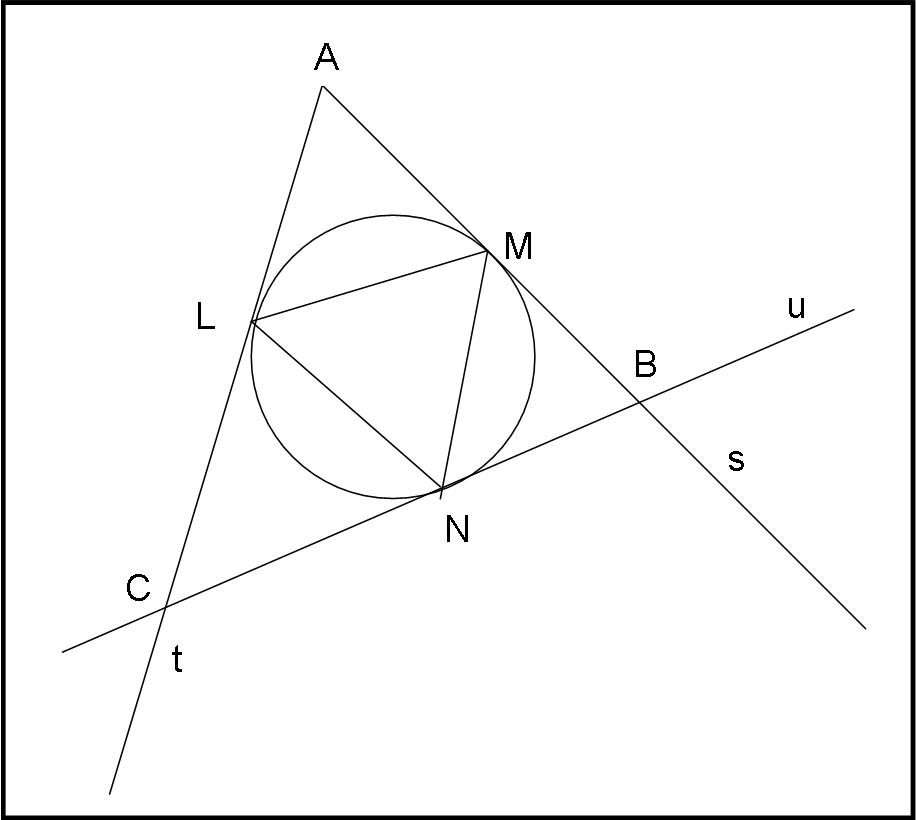
Segna un punto A qualsiasi esterno alla torta e traccia le due tangenti s e t alla torta, che la toccano nei punti L e M. Poi considera una retta u qualsiasi, anch’essa tangente alla torta nel punto N. Infine, congiunge i punti L,M e N,ottenendo un bel triangolo inscritto nel cerchio-torta. A questo punto consegna a Pippo il disegno e gli dice con un lieve sorriso: “Ecco la situazione che troverai stasera… Cerca di studiare molto bene i due triangoli ABC e LMN, perché mi dovrai rispondere al volo, avendo a disposizione solo un goniometro e una piccola calcolatrice elettronica”,
Pappo va nella sua stanza e inizia un’analisi approfondita della situazione. Al momento del taglio della torta sembra molto soddisfatto di sé. Ovviamente, la situazione che trova (Fig. 2) è del tutto diversa a quella del disegno (d’altra parte tutto ciò che era disegnato era da considerare “qualsiasi”).
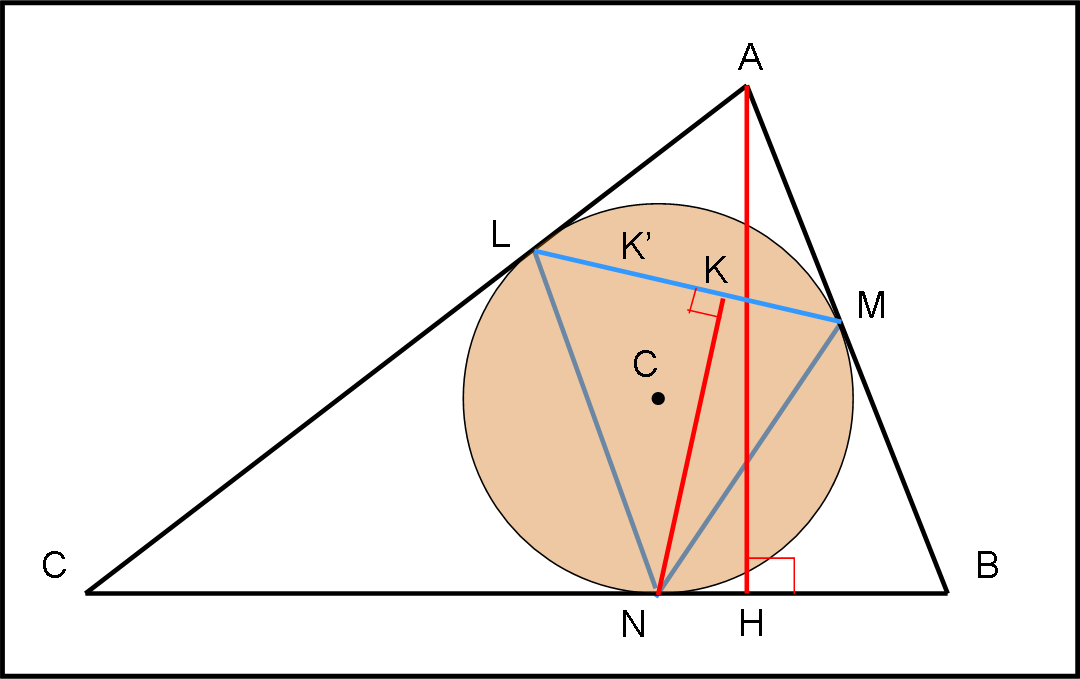
Attorno e sopra alla VERA torta sono tracciate le rette e segnati i punti come nel disegno pomeridiano. In più, però, sono state tracciate in rosso (succo di fragola?) due altezze dei triangoli, quelle che partono dal punto A e dal punto N, rispettivamente, ossia AH e NK.
La domanda che pone Pippo non sembra sorprendere più di tanto Pappo, che la lo sguardo risoluto. Pippo chiede con fermezza: “Usando solo il goniometro che hai in mano e la piccola calcolatrice tascabile, dimmi in trenta secondi (o anche meno) qual è il rapporto tra NK e AH?”
La risposta di Pappo è rapidissima ed … ESATTA!
Pappo tenta di metterlo in difficoltà e cambia velocemente la retta u e quindi i punti B e C e N, come mostra la Fig. 3.

Ripete la domanda, ma Pippo è un vero fulmine e dà nuovamente la risposta esatta.
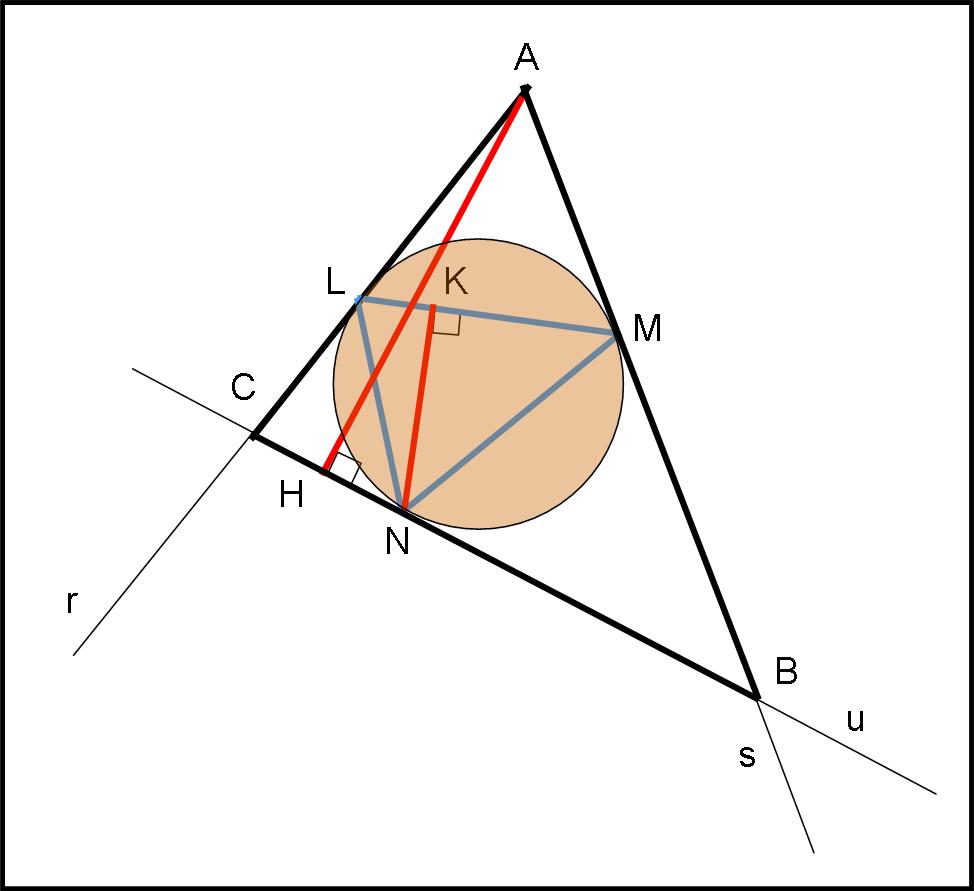
Pappo è disperato, cambia anche il punto A e la figura si trasforma totalmente come mostra la Fig. 4. Pochi secondi e Pappo risponde nuovamente esattamente.
Pippo vorrebbe anche modificare il raggio della torta, ma sa ormai benissimo che Pappo non sbaglierebbe un colpo. Abbassa la testa e si dà per vinto! Pappo, che, in fondo vuole molto bene al fratello, che ha contribuito non poco alla sua abilità geometrica, gliene offre la metà, che viene accettata con un largo sorriso.
Qualcosa mi dice che la prossima volta, se ci sarà, le parti saranno invertite…
La domanda per i lettori è molto semplice (come domanda…): “Che cosa ha ricavato Pappo durante il pomeriggio, lavorando sul disegno, per risolvere tutti i tre i casi prospettati da Pippo, nelle diverse condizioni?”
Ovviamente, Pappo non aveva a disposizione nessun righello e nessuna squadra, durante la festa…
Il quiz si presta, molto probabilmente, a varie soluzioni e a generalizzazioni di diverso tipo. Mi aspetto che i soliti “maghi” e qualche outsider sappiano elaborare al massimo il problema dei due fratelli.
NOTA BENE: il goniometro viene usato per misurare un solo angolo e la calcolatrice per una sola funzione!
Soluzione QUI






11 commenti
Azzardo il ragionamento seguente...
Pappo ha studiato come esprimere le aree dei triangoli inscritto e circoscritto. poi ha valutato le altezze in funzione dell'area e della base di riferimento. Infine ha espresso il rapporto tra le due altezze ( NK e AH)
L'espressione del rapporto che ha ottenuto richiede solo la misura dei tre angoli del triangolo esterno (goniometro) e il calcolo di funzioni trigonometriche (coseno e cotangente) con la calcolatrice.
L'espressione del rapporto (chiamando α, β, γ i semiangoli del triangolo esterno alla torta) dovrebbe essere il seguente...
NK/AH = cosα cosγ * ( cotgα + cotgγ) / ( cotgα + cotgβ + cotgγ )
Salvo errori nei miei calcoli. Naturalmente, appena riesco a usare Latex, o trovo il modo di scrivere bene le formule, seguirà la dimostrazione.
Ho aggiunto una Nota Bene nell'articolo per renderlo più semplice ee non partire per la ... tangente. Ripeto qui la nota:
Il goniometro può misurare un solo angolo per ogni torta. La calcolatrice serve solo per una funzione. Insomma, veramente pochi secondi da spendere davanti alla torta, prima di dare la risposta!
il mio contributo alla discussione:
Bravo Arturo.... a questo punto non sono rimaste neppure le briciole
Mi resta la curiosità malsana di sapere se
cosα cosγ * ( cotgα + cotgγ) / ( cotgα + cotgβ + cotgγ ) è proprio 1/sen x
(che nella mia notazione sarebbe 1/sen β) ma non è proprio il caso di approfondire....
E io, invece, fossi in voi proseguirei... La dimostrazione che ho trovato io usa solo e soltanto la funzione SENO.
Inoltre, uno certo rapporto che non cambia al cambiare del triangolo, ma dipende solo da un angolo, sono convinto possa dar luogo a qualche animazione interessante...
Una animazione che forse può suggerire qualche idea all'amico Arturo...
Dopo aver fatto scivolare gli estremi di AH e NK fino al punto L, avere riportato AH in LD...
Si tratta "solo" di dimostrare che l'angolo LDN è uguale ad alfa (!) per dire che NK = AH sen(alfa)
Questo sarebbe vero se LD fosse perpendicolare ad AB.
C'è anche da considerare il suggerimento di Enzo:
Inoltre, uno certo rapporto che non cambia al cambiare del triangolo, ma dipende solo da un angolo...
consiglio... basta un bel teorema di Euclide e una similitudine di triangoli (un po' strani) e buttiamo via tutto fuorché il seno....
Poi l'animazione viene di conseguenza... (forse)...
Magari chiedere a Oreste, l'amatematico ????
cari maghi,
sfruttando qualche uguaglianza tra segmenti si possono eseguire interessanti animazioni...
Forza, cercate una soluzione probabilmente più semplice (serve solo il seno!). E poi via con le animazioni... (io non ne sono capace...).
Non avendo idee migliori per trarre vantaggio dai consigli di Enzo, ho consultato Oreste. Dopo averci pensato un po' mi ha fatto questo disegno.
Poi mi ha detto: adesso però non ho tempo perché devo andare a tenere una conferenza sul "Il gianduiotto e le sue relazioni con l'inconscio".
Ti resta "solo " da dimostrare, se riesci, che l'angolo WKN vale alfa, così avresti due triangoli simili: WKX e NHX e poi... poi hai quasi finito. Ciao! Ed è uscito di corsa.
Al momento non vedo come se ne venga fuori, ma se ad Arturo viene qualche idea...
Comunico che Oreste è tornato e ha detto che se solo si riuscisse a dimostrare che nella figura precedente i due triangoli rettangoli ZWH ed LKN sono uguali , allora WK = HN, e pertanto si otterrebbe il rapporto cercato KN/AH = sen (alfa).
Ho evitato di contrariarlo....
la vedo difficile... e se cambiasse triangoli ?