Dopo le gare ad inseguimento tra i soli veri e i soli finti della scorsa puntata, ora Pautasso dovrà vedersela con le terribili sinusoidi, insinuanti e sinuose curve che gli ricordano tanto le dolorose sinusiti della sua infanzia.

Ma se la caverà anche questa volta.

 

Capitolo 5

 

Mattia osservò il disegno tracciato da Pautasso con evidente soddisfazione.

“Benissimo, Oreste, questo diagramma rappresenta proprio gli anticipi e i ritardi, che ciclicamente si verificano esclusivamente a causa della ellitticità dell'orbita. Infatti se l’orbita fosse circolare, la Terra si muoverebbe di moto circolare uniforme e gli orologi andrebbero d’amore e d’accordo con il Sole vero. Se rappresentiamo questi anticipi e ritardi con un grafico, mese dopo mese, abbiamo una curva che parte da zero, raggiunge un massimo, ripassa da zero e raggiunge un minimo e, infine, torna a zero chiudendo il ciclo. In pratica è una sinusoide.”

Pautasso annuì. “Eh sì, la sinusoide è una brutta bestia, io l'ho avuta da piccolo, un mal di testa, ma un mal di testa...”

“Oreste, non ho detto sinusite, ma sinusoide. E' una curva che sembra una S sdraiata, parte da zero arriva al massimo, poi scende, ripassa da zero, quindi tocca il minimo e torna a zero. Guarda, te la disegno...”

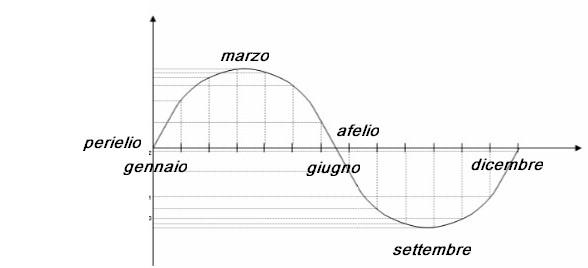
“Ho capito, una S sdraiata, però sarebbe più una Z sdraiata, e “arrotondata”, secondo me.”

“Va bene, andiamo avanti. Gli scostamenti massimi nella culminazione sono dell'ordine di alcuni minuti. Da da gennaio a marzo i ritardi si accumulano fino ad un massimo di 7 minuti a fine marzo. Poi iniziano i giorni con anticipi che riducono il ritardo raggiunto e, a fine giugno, lo riportano a zero. Gli anticipi proseguono ad accumularsi fino a settembre, raggiungendo il massimo di 7 minuti. Da questo punto in poi tornano in gioco i ritardi che, un po' per volta, fanno diminuire sempre di più l'anticipo, fino ad annullarlo alla chiusura del ciclo.”

“Ma come facciamo a “vedere” la curva? Fino ad ora abbiamo solo i ritardi e gli anticipi...”

“Certo, fin qui abbiamo analizzato gli effetti di un’orbita ellittica e di un asse terrestre perpendicolare al piano orbitale. Per questo motivo l'altezza del Sole è sempre la stessa. Ma sappiamo che l’asse terrestre è inclinato rispetto al piano orbitale, ricordi? E’ per questo che abbiamo le stagioni ed è per questo che nella stagione invernale il sole è più basso sull’orizzonte e in quella estiva è più alto. Aggiungiamo questa informazione al diagramma che avevi tracciato per indicare gli spostamenti in anticipo e in ritardo e, invece di una semplice linea orizzontale, vedremo una curva a forma di ellisse. “

Mattia disegnò la curva qui sotto.

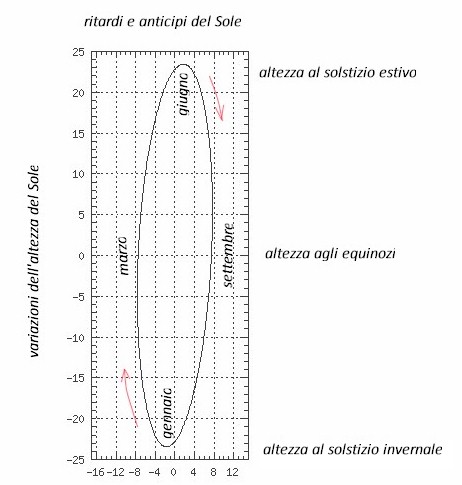
“Non abbiamo ancora finito, Oreste, la realtà è più complicata e adesso viene la parte più difficile...”

Il sorriso che fino a quel momento aveva illuminato la faccia di Pautasso si smorzò. Ma come, sembrava tutto risolto... Aveva anche capito al volo l'ultimo disegno di Mattia, con quella ellisse birbacciona (certo che queste ellissi non finiscono mai...). E, proprio adesso, salta fuori che la parte difficile deve ancora cominciare, oh basta là...

“Scusa Mattia ma non basta così? Cosa c'è ancora da dire?”

“Adesso faremo il contrario, cioè studieremo il caso di un'orbita circolare, con il Sole nel centro, e vedremo come influirà, sull'istante di culminazione, il fatto che l'asse terrestre risulti inclinato come è in realtà.”

“Ma non l'abbiamo appena visto..?”

“Solo in parte, Oreste, solo in parte...”

“Oh basta là!”

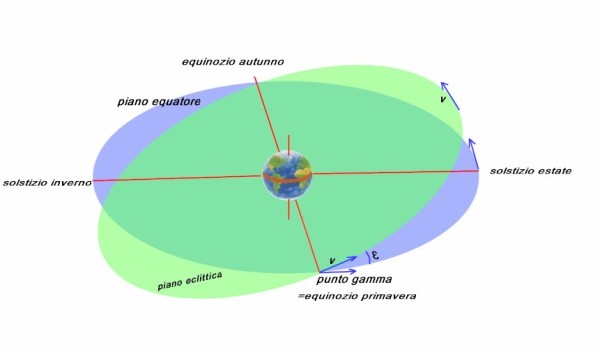
“Dai, Oreste ! Abbi ancora un po' di pazienza... Ecco, guarda questa figura, rappresenta la situazione dal punto di vista della Terra (al centro). Il Sole è visto muoversi sul piano della eclittica (verde), che non coincide con il piano equatoriale (azzurro), data l'inclinazione dell'asse terrestre.

Sul piano dell'eclittica il movimento del Sole descrive un cerchio (abbiamo detto che non teniamo conto della eccentricità ). Ma sul piano dell'equatore, che è inclinato di 23,5° questo cerchio appare come una ellisse”

Pautasso alzò gli occhi al cielo.”Ancora una ellisse !...”

“”Già, nota anche che i due piani si intersecano lungo una retta che passa per il centro della Terra. Vedi, in primo piano, quel “punto Gamma” , che coincide con l'equinozio di primavera? Ebbene è proprio da quel punto che incominciamo a valutare come il Sole si sposta apparentemente lungo l'ellisse nel piano equatoriale.”

“Però in realtà il Sole gira con una velocità costante lungo l'orbita circolare sul piano verde...”

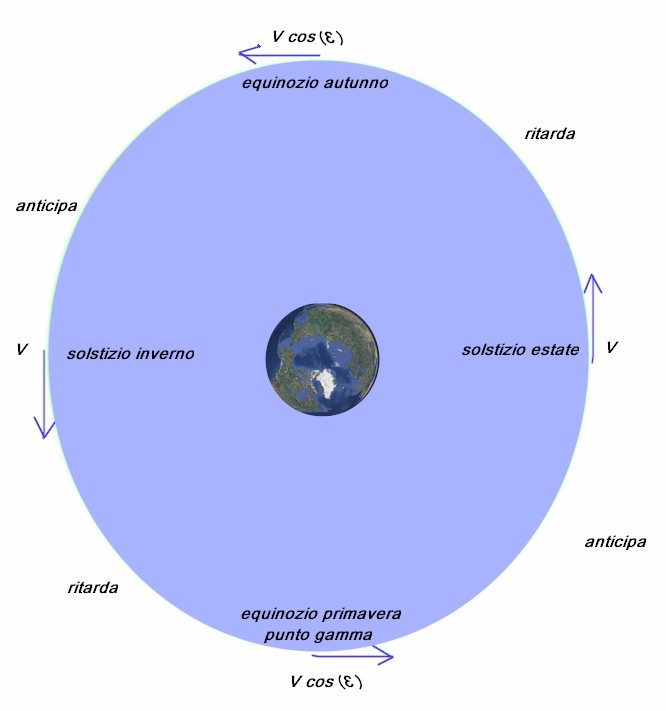
“Vediamo meglio, in pianta, la proiezione dell'orbita sul piano equatoriale, quello azzurro. Nota che siamo al di sopra del polo Nord terrestre” Disse Mattia. “Ebbene, mentre il movimento circolare, regolare, si svolge sul piano verde, contemporaneamente il Sole, che vediamo sul piano equatoriale qui sopra, azzurro, si muove lungo l'orbita ellittica. Quando i due piani si intersecano (agli equinozi) la proiezione della velocità sul piano equatoriale sarà V cos(ε), dove ε vale 23,5°, al suo valore minimo. Invece, al passaggio ai solstizi, l'orientamento della velocità proiettata sul piano equatoriale ed il suo valore (massimo), coincideranno con quelli sul piano dell'eclittica.”

“Ma allora, Mattia, la velocità della proiezione del Sole sul piano equatoriale non è mai superiore a quella del Sole? Se è così come avviene il recupero dei ritardi?”

“Bravissimo Oreste! Infatti ci resta ancora una cosa da dire... La velocità di cui abbiamo parlato è quella tangenziale e non quella angolare! Se le due velocità tangenziali sull'eclittica e sulla sua proiezione sono uguali, come avviene ai solstizi, la velocità angolare sarà superiore sul piano della proiezione, perché in quei punti, dove l'ellisse è più “schiacciata” il raggio dell'orbita è più piccolo e, a parità di velocità tangenziale, la velocità angolare sarà più grande.

* (vedi nota a fine pagina)

"Allora, Mattia, appena il Sole “proiettato” parte da questo punto gamma e si dirige verso il punto del solstizio estivo, comincerà a muoversi lentamente e poi andrà accelerando. Quindi all'inizio vedrò il sole "vero" in anticipo ma poi l'anticipo si ridurrà e al solstizio si sarà annullato.”

“Proprio così , Oreste. Superato poi  il punto del solstizio, alla massima velocità,  il sole "proiettato" comincerà a rallentare. Quindi, osservando il sole "vero",  noteremo  un ritardo iniziale che poi calerà fino ad annullarsi all'equinozio di autunno, diametralmente opposto al punto gamma. E così via.”

 

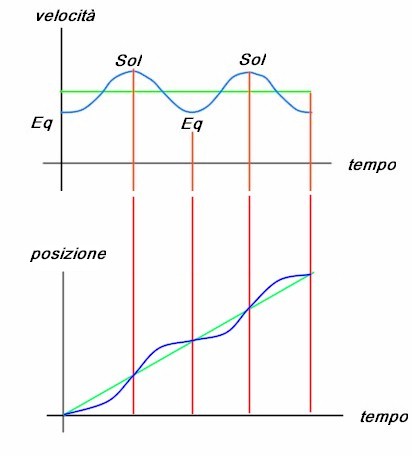
“Allora ci saranno quattro punti in cui non abbiamo né ritardo né anticipo? Cioè gli equinozi e i solstizi?”

“Precisamente, ci saranno due massimi e due minimi, due cicli completi della sinusoide, Solo ai solstizi e agli equinozi non avremo ritardi o anticipi.

“Ho capito, la sinusoide dell'eccentricità, la prima che abbiamo disegnato, ovvero quella generata dalla forma ellittica dell’orbita terrestre, è semplice, questa invece è doppia.”

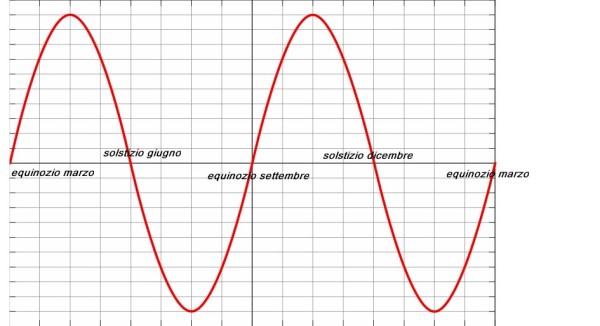
“E' proprio così, due cicli completi”

“E il disegno della posizione del Sole, come lo faccio, adesso?”

“Oh, Oreste, per questo devi solo abbinare ad ogni giorno i suoi due valori di altezza sull'orizzonte e di anticipo o ritardo, dovuto solo all'effetto dell'inclinazione dell'asse, alla sua obliquità. Ti posso ancora dire che nei momenti di maggiore scostamento il Sole ritarda o anticipa di circa 10 minuti.”

“Cari amici lettori, cosa posso dirvi.... Aiuto!!! il cognato mi chiede di fare un disegno, come quell'altro di ieri, ma che tenga conto che in inverno il sole è basso, che in estate è alto che in primavera e autunno è giusto. In più bisogna pensare che ritarda tanto o anticipa tanto tra equinozi e solstizi ma poi, proprio in quei momenti lì, è zero ! Ma, insomma, cosa pretende? Aiutatemi voi che a me è tornato il mal di testa come quando avevo la sinusoide!”

* Nota 
Un nostro lettore , "starlight" , ha fatto rilevare un passaggio fuorviante nella versione  originale di questo dialogo.
Il testo era il seguente...

“Allora, Mattia, appena il Sole “proiettato” parte da questo punto gamma e si dirige verso il punto del solstizio estivo comincerà a muoversi lentamente e poi andrà accelerando. Quindi all'inizio lo vedrò in anticipo ma poi l'anticipo si ridurrà e al solstizio si sarà annullato.”

“Proprio così , Oreste. Superato il punto del solstizio alla massima velocità, comincerà a rallentare. Quindi avremo un ritardo iniziale che poi calerà fino ad annullarsi all'equinozio di autunno, diametralmente opposto al punto gamma. E così via.”

La giusta osservazione del lettore era questa...

Ecco, questo concetto fatica un po' ad entrarmi in testa. 
Cominciamo dalla prima frase. 
Preciso che io parto dal presupposto che il Sole torna prima sul Meridiano di partenza (e quindi anticipa) se aumenta la sua velocità. Quindi più accelera e più dovrebbe anticipare, vi trovate? Dalla prima definizione del blog però non sembra essere così; infatti dice che a partire dal punto gamma il Sole anticipa, man mano che si avvicina al solstizio d'estate però il Sole accelera e l'anticipo si riduce fino ad annullarsi: ma non dovrebbe essere il contrario? Cioè se il Sole accelera dovrebbe anticipare ancora di più quando si avvicina al solstizio d'estate, e non ritardare, no?

Lo stesso dicasi per la seconda frase del blog: 
superato il solstizio d'estate la velocità inizia a rallentare e quindi il Sole ritarda. Ma man mano che rallenta però questo ritardo diminuisce fino ad annullarsi all'equinozio d'autunno. Anche qui ripeto la stessa domanda a parte invertita: il ritardo non dovrebbe aumentare man mano che la velocità diminuisce?

Per evitare fraintendimenti, il testo dei due paragrafi è stato riscritto in modo da esprimere ciò che si intendeva dire realmente, ed  è quello che ora appare nell'articolo.

Grazie, starlight, continua a seguirci,  vorremmo avere tanti lettori attenti come te....

QUI  trovate gli altri articoli dedicati alla scoperta dell'analemma da parte di Oreste Pautasso

QUI potete trovare racconti di vario tipo dello stesso autore, Mauritius, insieme a quelli di Vin-Censu