Quiz: Quazel al Casinò ***/****
Dopo un lungo peregrinare sul nostro pianeta, Quazel ha scoperto che molte persone hanno l'abitudine di giocare i propri soldi nella speranza di ottenere un guadagno. Trovando la cosa piuttosto curiosa, decide di approfondirne la conoscenza. Perciò si fa prestare dei soldi dal suo amico scienziato e, lasciata la sua astronave nel parcheggio, entra al Casinò. Qui scopre che i tipi di giocate che si possono fare sono molti, ma non conoscendo il meccanismo di nessuno di essi, prima di mettere a rischio i suoi soldi, vuole informarsi bene.
Il primo gioco proposto dal croupier è quello del rosso-e-nero. Tale gioco è analogo a quello chiamato testa-o-croce, che consiste nel lanciare una moneta: prima del lancio il giocatore sceglie su cosa puntare, poi si lancia la moneta . Nel caso che il risultato del lancio corrisponda alla previsione, il giocatore vince la somma che costituiva la posta, ad esempio un Euro, in caso contrario la perde.
L'analogia però non è perfetta perché, nel gioco del rosso-e-nero, i casi favorevoli non sono la metà, come nel gioco della moneta, ma un po' meno, dato che oltre ai numeri rossi e neri, entra in gioco lo zero, che non è né rosso né nero. Se esce lo zero il giocatore perde la posta.
Quando il croupier gli chiede se vuol giocare al rosso-e-nero, Quazel risponde di no, perché perderebbe sicuramente. Ecco come lo spiega:
" se le probabilità fossero le medesime del gioco testa-o-croce potrei giocare, anche se sarebbe inutile. Supponiamo infatti di giocare a testa-o-croce, puntando un euro alla volta, avrei il 50% di possibilità di vincere 1 Euro e il 50% di perdere 1 Euro, quindi di vincere -1 Euro. Mettiamo che giochi 10 volte, è plausibile aspettarsi di vincere almeno cinque volte. In tal caso vincerei cinque Euro e perderei cinque Euro. Se facciamo i conti guadagno 1*5 - 1*5=0 , quindi alla fine non avrei concluso niente."
Ma con il rosso-e-nero è ancora peggio; andrei in perdita. Infatti ci sono 36 numeri più lo zero; 18 sono rossi e 18 sono neri, è poi c'è lo zero. Perciò i numeri, in tutto, sono 37. Quindi, sia che io giochi sul rosso, sia che giochi sul nero, avrei solo 18/37 possibilità di vincere. Se, tanto per semplificare i calcoli, facessi 37 giocate avrei un guadagno di 1*18-1*19=-1 <0. E avrei perso.
Allora il croupier gli propone "prova a puntare su un numero: se esce vinci 35 volte la posta." Quazel, istintivamente, risponde: "Non sono mica scemo, ho una possibilità di vincere su 37 : giocando 37 volte potrebbe uscire almeno una volta il mio numero, ma avrei perso fino ad allora 36 Euro e, vincendo, ne prenderei solo 35! A questo punto il croupier tenta l' ultima chance. "Ti permetto di giocare al raddoppio, sul rosso-e-nero; ogni volta puoi raddoppiare la posta cosi sei sicuro che non perderai mai e avrai un guadagno assicurato. Ti spiego come funziona in dettaglio:
Puoi giocare un Euro (puntata minima) su rosso o nero. Se vinci incassi una quota uguale a quella puntata, altrimenti perdi la quota puntata. Se perdi puoi giocare 2 euro; se perdi ancora 4 euro; e così via, raddoppiando ogni volta. In ogni caso la tua vincita copre tutte le perdite precedenti. Il gioco finisce quando o finisci i soldi o effettui una vincita. Poi si può ricominciare da capo. Se per esempio perdi alla prima , seconda, terza e quarta giocata, perdi 1+2+4+8=15 Euro, ma se vinci alla 5 giocata, in cui punti 16 Euro, ne vincerai 16 e alla fine guadagni 1 Euro. Il guadagno è poco, ma sicuro!"
(ribadisco una cosa importante; il gioco non consiste nella singola puntata , ma comincia con una puntata e finisce o quando il giocatore finisce i soldi, o quando azzecca la previsione sul'uscita del rosso o del nero)
Quazel risponde: No per due motivi. Il primo è che ho solo 31 Euro, non una cifra illimitata di soldi. Il secondo è perché non recupererei nemmeno quello che ho giocato. Tanto varrebbe giocarli tutti assieme sul rosso o sul nero. Questi giochi non fanno per me; restituirò la somma al mio amico scienziato.
Perché Quazel non accetta di giocare al raddoppio? Eppure intuitivamente è conveniente, basta pensare che non tutti i casinò lo permettono. Nell'ambito della teoria dei giochi questo è un problema noto, anche se però le soluzioni si affidano a tecniche molto complesse.
Chiaramente la soluzione di questo quiz non è un numero né una formula. Si tratta di valutare, servendosi di calcoli o ragionamenti, perché sia valido il buon senso di Quazel. Sono ammesse anche simulazioni.
QUI la soluzione del quiz
QUI tutti i quiz del club dei maghi, QUI tutti i quiz del blog
27 commenti
un quiz un po' strano che servirà anche per introdurre un nuovo argomento: Il calcolo delle probabilità, fra l' altro non strettamente necessario per esprimere una opinione sensata sul problema.Invito anche tutti gli autori a partecipare , e visto che non esiste una soluzione unica, anche subito.
Non fornisco in questo commento alcuna risposta sui motivi per cui che non conviene giocare, come sostiene Quazel, ma solo alcune considerazioni a corollario del quesito posto.
Il gioco è costituito da una serie di sequenze, ciascuna delle quali è articolata su un numero finito di puntate che dipende dal capitale a disposizione.
Supponiamo che la prima puntata sia di 1 Euro. Se perdo punto il doppio e vado avanti così fino a quando vinco. In quel momento avrò vinto 1 Euro con cui incremento il capitale iniziale. Però potrei non essere in grado di proseguire fino alla vincita, perché ad un certo punto i soldi che mi restano non sono sufficienti per giocare il doppio dell'ultima somma puntata. In questo caso potrei solo ripartire con una nuova sequenza puntando inizialmente, secondo la regola stabilita, 1 Euro nella speranza di recuperare.
Per sapere quante puntate sono possibili avendo un certo capitale a disposizione, devo trovare la potenza di 2 che più si avvicina, senza superarlo, al valore di questo capitale.
Ad esempio se ho 150 Euro, la potenza più vicina è 128, cioè 2^7. Questo significa che, nell'ipotesi di dover rilanciare perché non ho vinto, potrò giocare 7 volte ( 6 rilanci) . Nelle sette giocate sfavorevoli avrò perso 1+2+4+8+16+32+64 = 127 Euro, me ne rimarranno 150-127=23, che non bastano per proseguire.
Aggiungo solo la considerazione che si può vincere con una certa probabilità, con un numero di giocate inferiore al numero massimo consentito dal capitale disponibile, ma si vince sempre soltanto 1 Euro.
Nel caso del precedente esempio, se perdo 127 dei miei 15o Euro e me ne restano 23, avrò a disposizione solo 4 giocate nella nuova sequenza ( la potenza di 2 in questo caso è 16 = 2^4 e mi consente 3 rilanci). Se non vinco neppure ora, mi resteranno 23 - 1 - 2- 4 - 8 = 23-15 = 8 Euro.
Se voglio giocare anche questi 8 Euro inizierò la terza sequenza e, dato che 8 è proprio una potenza di 2 = 2^3 potrò fare tre tentativi ( 2 rilanci). Fallendoli mi resterà solo 1 Euro ( 8 - 1- 2-4 = 8 -7 = 1)
Con l'Euro superstite potrei prendere un caffè, oppure giocare (solo una volta) e, se non vinco neppure ora andrò a zero.
In conclusione per 7+4+3+1 = 15 volte consecutive non ho mai vinto e ho perso tutti i soldi.
Questo è il caso più sfavorevole, naturalmente. Occorre ragionare su come e quanto incidono sul risultato le eventuali vincite. Riusciranno a compensare le perdite e a farci diventare ricchi, oppure non faranno che ritardare l'esito finale di perdere tutto il capitale?
Son d'accordo con Quazel.
Se tutto va nel migliore dei modi vinco un 1 euro, non di più.
Per esempio:
alla seconda giocata ho già perso 1 euro (nella prima giocata), se vinco mi danno 2 euro (2-1= 1 euro);
alla terza giocata ho già perso 3 euro (1+2), se vinco me ne danno 4 (4-3 =1);
alla quarta giocata ho già perso 7 euro (1+2+4), se vinco me ne danno 8 (8-7=1);
alla quinta giocata ho già perso 15 euro (1+2+4+8), se vinco me ne danno 16 (16-15=1).
La sesta giocata richiede 32 euro, ma io ho già perso tutti i soldi (1+2+4+8+16 = 31).
Cosa vince invece il banco?
Se io non riesco entro 5 volte a vincere, si porta a casa un malloppo decisamente più consistente, ossia tutti i miei 31 euro.
Quindi rischio 31 euro per vincerne al massimo 1.
Paolo
Ops, dimenticavo, ammettiamo di usare più sequenze... ossia di vincere entro le 5 volte e di avere così 32 euro a disposizione e ripartire, potrei arrivare fino alla sesta giocata:
La sesta giocata richiede 32 euro, io ne ho già persi 31 (1+2+4+8+16 = 31)....
Anche ammettendo di vincere ed arrivare così a 33 euro, questi non sono sufficienti per accedere alla settima giocata, che richiede 64 euro..
Dovrei vincere almeno 33 sequenze per raccimolare 64 euro (31+33) ed accedere alla settima giocata ed anche vincendo porterei a casa solo 1 euro in più rispetto a quelli già raccimolati, infatti la settima giocata richiede 64 euro, ma io ne ho già persi 63 (1+2+4+8+16+32= 63)....
Per accedere alla successiva giocata avrei bisogno di 128 euro....
Insomma il gioco è tutt'altro che conveniente per Quazel.
Paolo
Si potrebbe fare questo ragionamento:
Inizio a giocare con il capitale di 31 Euro
Quale probabilità ho alla prima giocata di perdere? Dato che ci sono 18 numeri a mio favore e 19 (comprendendo lo zero) contro, la frequenza relativa sarà 19/(18+19) = 0,5135.
Proseguendo i rilanci senza vincite, la probabilità di arrivare a 5 risultati negativi consecutivi sarà
0,5135 ^5 = 0,0357.
Se va male i cinque lanci mi sono costati 1+2+4+8+16= 31 Euro
Però al quinto lancio potrei vincere. In questo caso con la vincita di 16 Euro coprirei le perdite precedenti di 15 Euro e mi resterebbe un guadagno di 1 Euro. Il capitale disponibile salirebbe così a 32 Euro.
Siccome la probabilità di 5 lanci consecutivi sfavorevoli è 0,0357, corrispondente a 1/28, significa che dopo 27 sequenze favorevoli ce ne sarà una sfavorevole.
Nelle 27 favorevoli ho accumulato vincite per 27 euro portando il capitale a 31+27 = 58. Ma con la sequenza sfavorevole verrei a perdere 31 Euro, rimanendo con 27 Euro. Quindi, rispetto all'inizio del gioco, avrei perso 4 Euro.
A questo punto ricomincio da capo, ma con un capitale più piccolo. Le successive ripetizioni del ciclo descritto portano inevitabilmente a perdere tutto il capitale.
Io la metterei così...
facciamo un caso limite che però si ripete anche per casi più positivi (all'inizio).
Quazel continua a perdere fino alla quarta giocata. Egli possiede ora solo 16 euro, giusto il valore della prossima puntata... Li gioca tutti, ovviamente e se perdesse ha perso tutto. Se invece vincesse guadagnerebbe 16 euro, portando il suo capitale a 32, che devo però giocare nuovamente tutti e via di seguito fino alla giocata in cui perderà e rimarrà a zero! In poche parole, ogni vincita gli permette solo di giocare ancora una volta, ma non può fermarsi e deve rigiocare sempre tutto quello che ha fino alla resa, in cui ha perso anche l'euro di inizio.
La cosa importante da capire è se può fermarsi e andarsene con i soldi rimasti (se vince entro la quinta giocata può farlo) o deve continuare a giocare anche se ha vinto. Sembrerebbe di no... ma non compreso perfettamente il quesito. Il fatto di avere 31 euro gli permette solo 5 giocate (se perdesse sempre)...
Ammetto che non mi è chiarissimo il problema...
Chiaramente il giocatore non è obbligato a far niente. Lui va al raddoppio per rifarsi della perdita. Ma per fissare le idee possiamo supporre che giochi finchè ha denaro, ovvero che faccia sempre finire la sequenza. Supponiamo anche che si accontenti della vincita di un euro, e poi se ne vada a casa. Poi torna ogni giorno per tutto l'anno. Alla fine dell'anno può avere un utile o no?
Il nostro amico non può mai vincere due puntate di seguito (deve fermarsi se vince). Il che vuol dire che non può che vincere un euro alla volta per definizione. Deve quindi sperare di vincere sempre entro le cinque puntate per aggiungere un altro euro al suo gruzzolo per ben 32 volte. Solo così avrebbe a disposizione i 32 euro che gli permetterebbero di puntare la sesta volta, avendo però perso le prime cinque. Se dovesse vincere guadagnerebbe un altro euro soltanto. Nuovamente dovrebbe vincere per ben 64 volte per sperare di puntare la settima. In poche parole (non ho tempo di fare i calcoli) per giocare più alto deve sperare di perdere la metà di ciò che ha e tentare l'ultimo colpo che se andasse male lo porterebbe nuovamente a zero.
Dovrebbe sempre vincere entro le prime cinque per ben 32 volte di fila, per poter tentare la sesta . Ma per puntare la sesta è obbligato a perdere le prima cinque puntate... e potrebbe perdere tutto ciò che ha guadagnato. Se gli andasse ancora bene, dovrebbe aspettare di vincere entro le sei puntate per potere avere a disposizione i soldi per la settima e via dicendo con un numero che continua a cresce. La prima volta che ci riesce, ma perde, tutto il suo malloppo si azzera.
Bisognerebbe calcolare le probabilità, ma penso che debba avere una fortuna mostruosa per non perdere tutto quando raggiunge la puntata di livello successivo (che è obbligato a fare...).
Qualcosa del genere... forse...
per dire la verità a questo non avevamo pensato.. ad un aumento di capitale progressivo. Il bello di questo quiz è che si apre a mille ipotesi-soluzioni, che restano comunque tutte valide. Forse è meglio pensare ad un tetto da rispettare e non superare, quello dei 31 euro .
Ecco alcune riflessioni, in generale, sull'argomento del quiz...
Considero un numero molto alto di giocatori che in un certo istante stanno giocando, non al raddoppio, ma semplicemente sul rosso o sul nero. Per ipotesi non esiste alcuna correlazione tra le loro scelte, ciascuno gioca indipendentemente. Mi aspetto che 19/37 giocatori stiano perdendo.
Questo fatto dovrebbe corrispondere alla probabilità di perdita ad ogni giocata per un singolo giocatore ed anche alla probabilità di perdita complessiva che un singolo giocatore, con eventuali interruzioni e riprese del gioco, nello stesso luogo o in un altro luogo, può attendersi alla fine di tutta la sua attività.
Quindi, se si giocasse sempre la medesima somma (senza regole di raddoppio) un elevato numero di volte, alla fine avrei perso 1/37 della somma di tutte le mie giocate. (potrei dire che perdo tutte le volte che esce lo zero e compenso le perdite e le vincite quando non esce lo zero)
Con la regola di raddoppiare la posta e ricominciare da capo se vinco, la situazione peggiora perché ad ogni passo rischio una somma crescente (potenza di 2) a fronte di una vincita costante ( puntata iniziale) e introduco il rischio di interruzione del gioco per raggiunto limite della disponibilità del capitale (residuo) da giocare, cosa che si riflette in una perdita secca che va a sommarsi alla perdita “programmata” causata dallo zero.
Ma a parte questi ragionamenti, tornando al gioco senza raddoppio, la cosa che incuriosisce è la seguente.
Il fatto che il giocatore, nella sua storia precedente abbia vinto o perso, non è ininfluente sul futuro. Se, alla fine, il valore a cui tenderà la perdita è 1/37, gli eventi futuri saranno in un certo modo compensativi di quelli passati. Questo indipendentemente dal fatto che il gioco venga interrotto e ripreso a distanza di tempo o si cambi il casinò in cui si gioca.
Direi che la sequenza delle uscite di rosso e nero si lega al giocatore come se esistesse una memoria , condivisa tra tutti i luoghi in cui può continuare a giocare, di ciò che ha realizzato fino a quel momento.
Non immagino, intuitivamente, che un giocatore veda oscillare continuamente il risultato complessivo, il bilancio di vincite e perdite, attorno allo zero. Credo sia una situazione piuttosto rara. Penso invece che per periodi abbastanza lunghi sia in positivo (giocatore fortunato) o in negativo ( giocatore sfortunato) e che, proseguendo per tempi ancora più lunghi, alla fine entrambe le situazioni convergano al medesimo risultato (perdita).
Dal che verrebbe da dire che il giocatore in perdita persiste, fino a rovinarsi, con una prospettiva che nel migliore dei casi sarà comunque una perdita, magari inferiore, ma non certo la vincita in cui spera.
Per contro, il giocatore in attivo avrebbe tutta la convenienza a smettere, per sempre, di giocare e non semplicemente di interrompere e riprendere in un momento successivo, illudendosi di “ricominciare da capo” e non dovere pagare, prima o poi, lo scotto della sua posizione favorevole.
Che ne pensate?
Tutto quello che è stato detto nei commenti fino ad ora è molto sensato, e abbiamo individuato il problema,ma per risolvere il quiz adesso servono i numeri. C'è un indice che ci può dire se giochiamo in perdita oppure no? Nella descrizione iniziale del quiz, quando Quazel analizza il testa o croce, fa un calcolo , supponendo di giocare 1 euro per 10 volte. Il calcolo è semplicemente questo: G= 1*5 - 1*5=0 quindi ci aspettiamo un guadagno zero. Nel caso del rosso o nero il calcolo che fa è questo: G=18*1-19*1=-1<0 quindi un guadagno negativo giocando 37 volte;che possiamo anche riscrivere con un rapporto per calcolare un valore medio:
Assumo valido il vincolo dei 31 Euro come limite.
Definisco:
giocata = singolo lancio con esito rosso o nero o Zero
ciclo = serie di giocate consecutive con raddoppio fino al limite consentito dal capitale disponibile
sequenza = ripetizione di cicli della medesima lunghezza (numero di giocate)
Inizio con capitale 31 Euro e cicli da 5 giocate.
La probabilità di perdita totale del capitale è (19/37)^5=3,6% , se perdo 5 giocate consecutive.
Significa che in una sequenza di 28 cicli ne vinco 27 e ne perdo 1
Bilancio della sequenza = + 1 Euro*27 – 31 Euro*1 = -4 Euro.
Al termine di questa sequenza (di 28*5= 140 lanci) il capitale scende a 31-4 = 27 Euro
Non è più possibile giocare cicli da 5 lanci ma solo da 4.
La probabilità di perdita totale del capitale è (19/37)^4 = 6,9% , se perdo 4 giocate consecutive.
Significa che in una sequenza di 14 cicli ne vinco 13 e ne perdo 1
Bilancio della sequenza = + 1 Euro*13 – 15 Euro*1 = -2 Euro.
Il capitale residuo di 27-2 = 25 Euro consente di ripetere la sequenza più volte fin quando non scende al di sotto di 15 Euro. Ciò avverrà dopo altre 6 sequenze di questo tipo.
Al termine di questo gruppo di 7 sequenze (7*14*4 = 392 lanci) l capitale scende a 13 Euro
A questo punto si possono fare cicli da sole 3 giocate
La probabilità di perdita totale del capitale è (19/37)^3=13,5% , se perdo 3 giocate consecutive.
Significa che in una sequenza di 7 cicli ne vinco 6 e ne perdo 1
Bilancio della sequenza = + 1 Euro*6 – 7 Euro*1 = - 1 Euro.
Il capitale residuo di 13-1 = 12 Euro consente di ripetere la sequenza più volte fin quando non scende al di sotto di 7 Euro. Ciò avverrà dopo altre 6 sequenze di questo tipo.
Al termine di questo gruppo di 7 sequenze (7*7*3 = 147 lanci) il capitale scende a 6 Euro
Dopo 140 + 392 + 147 = 679 lanci restiamo con meno del 20% del capitale iniziale.
La legge di decadimento può essere descritta come una linea spezzata con andamento decrescente in cui ogni tratto ha una pendenza espressa da perdita/ N. giocate
Il capitale parte da 31 Euro e cala con pendenza = 4/140 = 0,0286.
Nel secondo tratto cala con pendenza = 13/392= 0,0332
Nel terzo cala con pendenza = 7/147=0,476
Mi verrebbe da dire : E così via …..
Provo a dire la mia con una tabella.
Nella spiegazione del gioco c'è scritto che finisco di giocare o perché vinco o perchè finisco i 31 euro a disposizione.
Con la tattica del raddoppio ho 5 giocate a disposizione come si vede nella riga "totale puntate". Se esce il colore giocato in una di queste giocate il risultato è positivo di 1 euro (differenza tra vincita e totale puntato). Se non vinco neanche alla 5a devo abbandonare lasciando al casinò i miei 31 euro.
Ma quale è la probabilità che accadano questi 6 tipi di uscita dal gioco? (Vincita alla 1a, 2a,...5a giocata, uscita per fine risorse)
La probabilità di vincita alla prima giocata è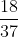
. La probabilità di vincita alla seconda giocata è la probabilità di avere perso la prima e vinto la seconda cioè 
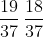. La probabilità di vincita nella terza è la probabilità di avere perso le prime due e vinto la terza cioè ^2\,&space;\frac{18}{37})
. E così via per le restanti. Infine la probabilità di uscire per fine delle risorse è la probabilità di perdere tutte le 5 giocate cioè ^5)
. La somme di tutte queste probabilità viene 1 poiché almeno uno di questi 6 casi avviene sempre. Questo è un buon indizio di essere sulla buona strada.
Se dovessi ripetere questa tattica per un numero grande di giorni o se fossi il casinò e volessi calcolare quanto mediamente lascia sul tavolo ciscun giocatore che usa questa tattica dovrei moltiplicare il risultato di ciscuna tipo di uscita dal gioco per la sua probabilità e sommare il tutto.
A me viene che perderei mediamente circa 0,14 euro per giornata di gioco o il casinò guadagnerebbe circa 0,14 euro per giocatore che usa questa tattica.
Spero di essere sulla buona strada. Con le probabilità è facile trascurare qualche condizione ed arrivare a risultati sbagliati.
Secondo me si perde sempre: non vorrete stare tutta la notte al Casinò senza nemmeno bervi un bicchiere di vino?
quante belle risposte.. Per il momento chiaramente non possiamo dire niente. Però l introduzione del valore medio è fondamentale
Immagino che intendi il valore medio di perdita su un certo numero di giocate, ad esempio rispetto alle giocate fatte fino ad un certo momento.
Ad esempio: il valore medio della perdita giornaliera di 0,14 Euro che cita Fabrizio nel caso di giocate con 5 lanci, valore su cui mi trovo d'accordo perché nel mio ragionamento dopo 28 cicli si perdono 4 Euro (che corrisponde ad una perdita media come quella calcolata da Fabrizio), non resta inalterato nelle giocate future perché non saranno più possibili giocate composte da 5 lanci.
In altre parole: se mediamente perdo 0,14 Euro al giorno, ad un certo punto, diciamo una settimana, avrò materializzato questa perdita di 1 Euro Quindi avrò solo 30 Euro che non mi consentiranno di giocare per 5 volte come precedentemente. Questo fatto avrà una conseguenza sul valore medio.
Però l'osservazione di Givi, non è niente male. Non conosco il listino dei prezzi applicati al bar di un casinò ma non devono essere molto contenuti. Alla fine conta la vincita netta, considerando anche le spese accessorie...
bisognerebbe, per chi ha fatto i conti, provare gli stessi calcoli applicati al raddoppio con testa o croce..in questo caso il valor medio deve essere.. Questo costituirebbe un prova del nove
Con testa o croce la probabilità di perdere è 0,5 ad ogni lancio.
Perdo tutto il capitale di 31 Euro quando ho 5 lanci consecutivi sfavorevoli, con una probabilità (1/2)^5 = 1/32
Significa che su 32 lanci posso vincere 1 Euro per 31 volte e perderne 31 al lancio N. 32 Vincita totale = 0
Divido la vincita totale per i 32 lanci e ottengo media = 0
Nel fare il mio calcolo ho ipotizzato una situazione probabilmente più semplice rispetto di quella ipotizzata da Maurizio.
Nel mio caso in ciascuna tornata di gioco considero ripristinate le condizioni iniziali di 31 euro, indipendentemente dalla storia passata. Una tornata si ferma quando c'è una vincita o alla 5a puntata sfortunata. La tornata successiva riparte con 31 euro a disposizione e con una puntata di 1 euro.
Una ipotesi diversa, che credo sia quella di Maurizio, potrebbero essere quella di mantenere la memoria del gruzzolo accumulato fino al suo esaurimento o incapacità di consentire il raddoppio. Quindi in caso di vittoria si riparte da una puntata di 1 euro, ma con in dote il gruzzolo residuo senza ripristinarlo ai 31 euro, ne in positivo ne in negativo. In questo momento non ho idea di come trattare questo caso. Temo che sia molto più complesso di quello che ho trattato io.
Nei calcoli di come decade il capitale disponibile, contenuti in un precedente commento, ho fatto l'ipotesi che l'evento sfavorevole ( 5 perdite consecutive) si verificasse sempre alla fine. E' la condizione più favorevole per il giocatore, che ha tempo di accumulare 1 Euro per ciascuna vincita precedente.
Più realisticamente l'evento avverso potrebbe verificarsi a metà della sequenza.
In questo caso avremmo:
Capitale iniziale 31 Euro, cicli di 5 giocate. Numero di cicli favorevoli prima della perdita (27/2) con vincita complessiva di 13 Euro, seguita da perdita di 31 Euro che porta il capitale residuo a 13 Euro. (dopo 70 giocate) Perdita media in questa fase = (31- 13)/70 = 0,257 Euro/giocata.
Capitale residuo 13 Euro. cicli di 3 giocate. Numero di cicli favorevoli prima della perdita (6/2) con vincita complessiva di 3 Euro, seguita da perdita di 7 Euro che porta il capitale residuo a 13+ 3 -7 = 9 Euro. ( dopo 12 giocate) Proseguo con cicli da tre giocate ancora una volta, guadagnando 3 Euro e perdendone 7. Capitale residuo 9+3-7 = 5 Euro ( dopo altre 12 giocate). In questa fase di cicli da 3 lanci, in 24 giocate ho perso 8 Euro con una perdita media di 0,333 Euro/giocata.
Con un numero totale di 70+24 = 94 giocate ho perso 26 Euro, ossia quasi l'84% del capitale iniziale.
Proseguendo nel gioco arriverei molto rapidamente a perdere gli ultimi 5 Euro rimasti.
Capitale residuo 5 Euro , cicli da 2 giocate .
Numero cicli favorevoli prima della perdita ( 4/2) con vincita complessiva di 2 Euro, seguita da perdita di 3 Euro che porta il capitale residuo a 2 Euro. (dopo 6 giocate). In questa fase di cicli da due lanci, in 6 giocate ho perso 3 Euro con una perdita media di 0,5 Euro/giocata.
Ora, con capitale residuo di 2 Euro non posso più giocare al raddoppio. Posso solo giocare 1 Euro con la probabilità 0,513 di perderlo. Poi posso giocare l'ultimo Euro con le medesime prospettive. Quindi verosimilmente con 4 giocate perderò questi ultimi due Euro.
Riassumendo, ho giocato in totale 70+24+6+4 = 104 volte perdendo 31 Euro.
Ho impiegato 70 giocate per perdere i primi 18 Euro, 24 giocate per perderne altri 8, 6 giocate per perdere ancora 3 Euro e 4 giocate per perdere gli ultimi due Euro.
pur apprezzando l'estensione di Maurizio, confermo che il gioco si svolge come detto da Fabrizio, come scritto nel testo:
(ribadisco una cosa importante; il gioco non consiste nella singola puntata , ma comincia con una puntata e finisce o quando il giocatore finisce i soldi, o quando azzecca la previsione sul'uscita del rosso o del nero)
eventuali guadagni non vengono cumulati con il capitale a disposizione.Quanto alle storie passate, ricordo come abbiano portato alla rovina dei giocatori. Mi sembra comunque che stiamo centrando perfettamente il problema.
Visto che c'è ancora molto tempo (pensavamo di pubblicare la soluzione non prima di sabato), aggiungo una domanda; cosa cambia se uso un altro capitale iniziale? (da ritenersi comunque sempre costante nelle ripetizioni del gioco). Tanto per capirsi, parto sempre da 1 un euro, ma aumento il numero delle giocate possibili in modo che coprano più tentativi, quindi in generale con un capitale:
Avendo un capitale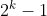
le giocate possibili, raddoppiando ogni volta, sono k.
Considerando che ad ogni giocata la probabilità di perdere è 19/37, la probabilità di perdere tutte le k giocate consecutive è^k)
.
Aumentando k sarà più improbabile perdere tutto il capitale, ma in caso di perdita si perderà una somma più ingente.
Si potrebbe esprimere l'esposizione al rischio E , considerando il prodotto tra il valore del capitale e la probabilità di perderlo, come segue:
Per fare alcuni esempi, partendo dal caso già studiato di k=5
La vincita che si può conseguire è sempre di un solo Euro, ma il capitale che viene messo a rischio nei tre casi varia da poche decine, a un migliaio, fino a un milione abbondante di Euro.
Per rispondere a questa ultima domanda utilizzarei questo schema che mi sembra possa semplificare il ragionamento.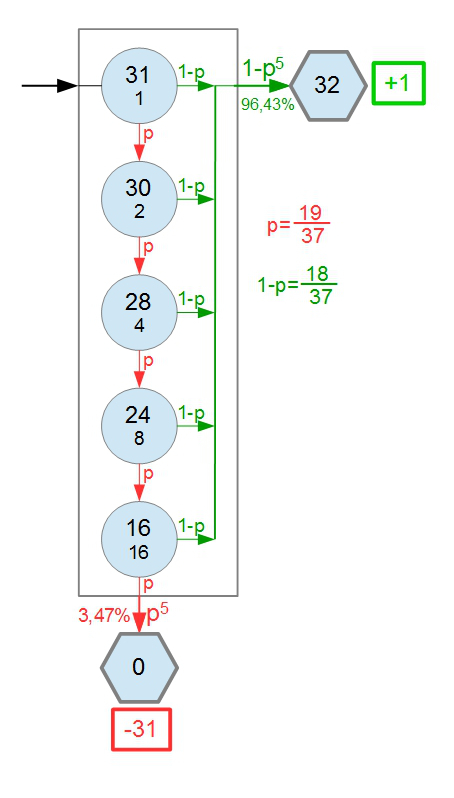
I cerchi rappresentano le giocate. I due numeri all'interno sono la somma disponibile prima della giocata e la puntata giocata. Se la giocata è positiva, allora esco dal gioco (esagono) recuperando il doppio della puntata. Se la giocata è sfavorevole, ritento (passo al cerchio sottostante) se posso raddoppiare la puntata, altrimenti esco perdendo i 31 euro.
La cosa che mi ha fatto vedere questo schema è che questo meccanismo è equivalente, dal punto di vista del risultato, ad un gioco con un unica puntata (rettangolo). La posta sono tutti i 31 euro. La vincita è la posta più 1 euro, la perdita è la posta intera. La possibilità di vincere o di perdere a questo gioco dovrebbero essere i valori vicino alle due frecce uscenti dal rettangolo.
La perdita si ha quando ci sono 5 risultati negativi consecutivi,)
. La possibilità di vincere non può che essere )
poichè è l'unica altra uscita dal rettangolo e la tornata di gioco è certo che avrà termine in una delle due uscite (o vinco o perdo).
Il risultato medio di questo gioco partendo da 31 euro è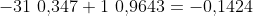
.
Se invece di partire da 31)
euro si partisse da un ammontare di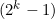 
, invece di 5 giocate avrei a disposizione k giocate. Nello schema in figura cambia la lunghezza della catena delle giocate che fa cambiare le possibilità di vincita o perdita e cambia l'ammontare della perdita che è sempre il totale del capitale iniziale, 
.
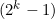La media del risultato diventa\,&space;p^k+1\,&space;(1-p^k)=1-(2p)^k)
. Nel caso di lancio della moneta, dove p=1/2 e 2p=1, la media dei risultati delle tornate è 0 indipendentemente dal capitale iniziale. Se la possibilità di perdere è maggiore di 1 volta su 2, come nel caso della roulette, al crescere del capitale iniziale la situazione lentamente peggiora. Con k=20, la media del risultato è circa -0,7.
Per giochi più rischiosi la perdita cresce molto di più rapidamente. Per un gioco con possibilità di vittoria 1 volta su 4, con k=20 la perdita media per tornata diventa più di 3000 euro contro i 6,5 euro per k=5.
Lo schema nella figura potrebbe essere lo spunto per rappresentare la modalità di gioco che riparte dal capitale accumulato. Invece dell'uscita dell'esagono in alto, ci dovrebbe essere una nuova catena. Ma la soluzione è lontana. Una cosa appare evidente. Sarà negativa in tutti i casi avendo solo uscite dal gioco con risultato negativo.
Scusate se mi sono fatto prendere la mano dal quiz molto interessante.
bellissimo quiz... complimenti! Non sono riuscito a partecipare attivamente, ma certo non sarei riuscito a competere con i maghi all'azione!!!
:-) :-)