Quiz: gli angoli di un parallelogramma *
Non vale la pena di scomodare i due fratelli golosi per questo quiz. E’ diretto ai meno esperti che abbiano, però, un lampo d’intuizione. Dopo due giorni via libera a tutti…
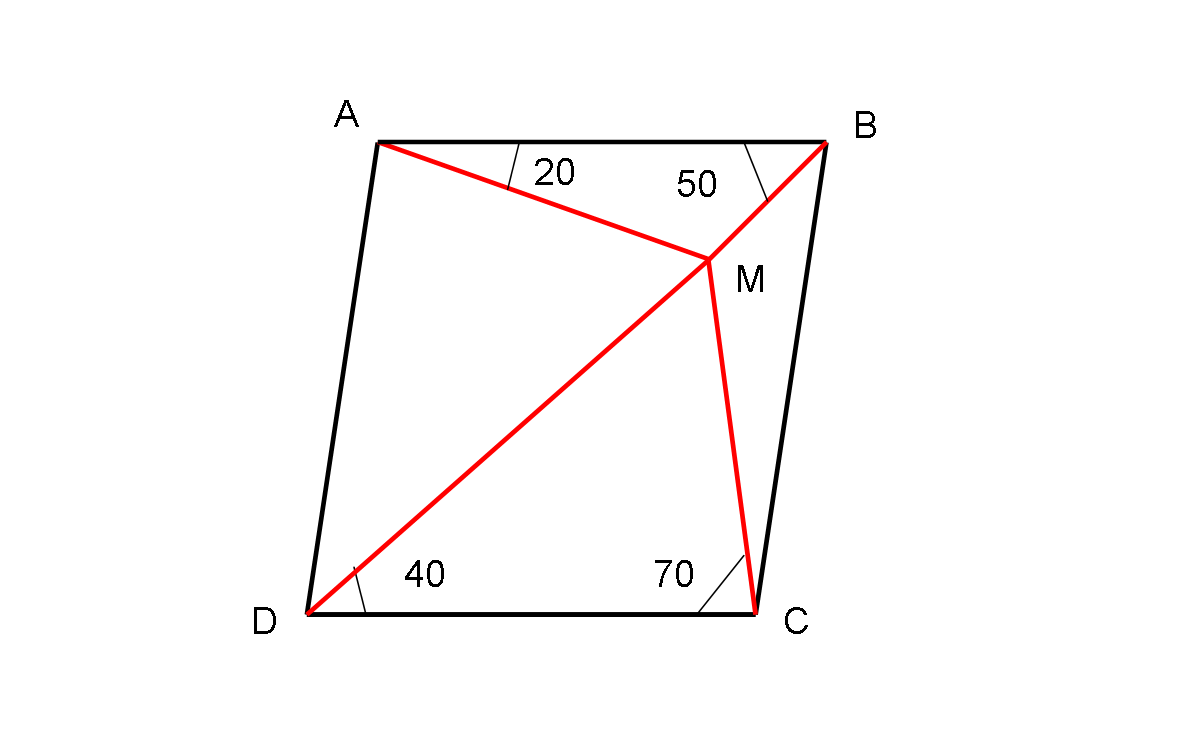
ABCD è un parallelogramma. M è un suo punto interno tale da formare gli angoli indicati in figura, tracciando le congiungenti con i quattro vertici.
Ditemi subito quanto valgono i quattro angoli del parallelogramma. Se volete, potete anche fare una figura esplicativa, ma è possibile dare la risposta solo con un’attenta occhiata… ovviamente spiegando il ragionamento fatto per la soluzione.
Soluzione QUI






7 commenti
beh, rompo io il ghiaccio...
io dico che gli angoli di questo strano parallelogramma sono tutti retti. Quindi alla fine il parallelogramma in realtà è un rettangolo.
Alla suddetta risposta, però, ci sono arrivato per via analitica, in particolare utilizzando il teorema dei seni. Allego foto degli appunti scritti a mano sul mio fido ultimo quaderno a quadretti. Ci sono arrivato anche utilizzando la geometria analitica (rette, punti etc) ma mi sembra più veloce il procedimento con il teorema dei seni.
Per quanto, invece, io abbia cercato l'attenta occhiata a cui fai cenno, caro Vincenzo, sinora non ho intravisto vie più o meno immediate. Ma sono sicuro che la via più semplice c'è, solo che non mi è ancora apparsa in testa
Se ridisegno la figura aiutandomi con un goniometro, salta subito fuori che i quattro angoli devono essere retti. In pratica, una volta disegnate le 4 semirette che si dipartono dal punto M, con le giuste inclinazioni indicate dai 4 angoli noti, stabilita a piacere la base AB (oppure la base CD), ottengo un parallelogramma (lati a due tra loro paralleli e congruenti) solo se i suoi 4 angoli sono retti, cioè alla fine ottengo un rettangolo.
ops... dimenticavo: negli appunti ho indicato con gamma l'angolo MBC e con beta l'angolo MCB (lettere come nella figura del quiz). Inoltre, ho preventivamente calcolato gli angoli con vertice M formati dalle semirette per M. In particolare, l'angolo DMC è pari a 70°, quindi il triangolo DMC è isoscele.
caro Arturo, proprio per questo parlo di risposta immediata... ovviamente senza goniometro a trigonometria...Comunque aver trovato il risultato aiuta per la strada più semplice e ancora più... ovvia
Caro Professore, lei è proprio diabolico, con questi disegnini anamorfici che fanno vedere gli angoli tutti storti.
Però, guardando il triangolo con gli angoli di 40° e 70° viene in mente che il terzo angolo dovrebbe essere di 180 -40-70 = 70° e quindi il triangolo dovrebbe essere isoscele, anche se non sembra proprio...
Quindi per farlo bello isoscele, tenendo ferm0 il lato AB, darei una spintina (verso destra) al lato DC fino ad allineare D sotto A e C sotto B ottenendo un rettangolo.
C'è anche da notare che sommando gli angoli noti nei due vertici opposti A e C si ottiene 90° e viene subito la voglia di provare a mettere alle incognite gli stessi valori scambiati. La stessa cosa vale per l'altra coppia di vertici B e D. Insomma, i conti tornano subito.
caro Sig. Oreste,
ammetto che lei usa parole un po' "rozze", ma estremamente efficaci (si vede che si è occupato di studi avanzati sul campo... vedi anatema solare). Io, nella mia rigorosità pseudo-scientifica avrei introdotto una proprietà dei quadrilateri iscritti in un cerchio... ma lei ha veramente le capacità dell'uomo di mondo... Ammetta di aver fatto il servizio militare a Cuneo!!!! Non può più nascondersi
Caro professor Vincenzo i poligoni sono la mia passione. Mi sono addirittura inscritto a quello di Bra, qui in provincia di Cuneo per esercitarmi ad andare a segno
Sì, sì, però, da uno come lei, così inscritto (e forse anche circon... ops, circoscritto) avrei preferito una dimostrazione meno empirica e più formale... E poi, scusi, spostare i lati di un parallelogramma senza nemmeno chiedergli permesso... Mi sa che più che uomo di mondo lei è un po' ... mondano!!
saluti, sempre dispettosi...