Siamo alla stretta finale, Oreste Pautasso, padroneggia ormai i misteri dell'analemma terrestre e, stimolato dalle domande di Mattia, giungerà addirittura a ragionare su analemmi di altri pianeti. Chi l'avrebbe mai immaginato...

 

Capitolo 6

 

 

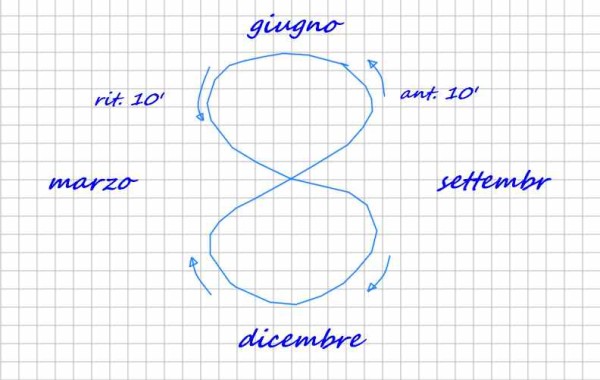
La luce del mattino entrava dall'ampia finestra del soggiorno, illuminando il disegno su carta a quadretti che Pautasso aveva tracciato con il pennarello blu, quello portafortuna, che il CAC distribuiva alle conferenze.

Mattia stava osservando il disegno, mentre Sofia, dopo aver portato in tavola la colazione, si dava da fare attorno alla stella di Natale che cominciava già a perdere qualche foglia.

“Forse l'ho bagnata troppo? O troppo poco? Questa pianta, non si sa mai come trattarla! Ieri sera le ho dato un bicchiere d'acqua...”

“Anche tu? Le chiese Mattia, perché l'ho bagnata anch'io...”

“Come, l'avete bagnata anche voi?! Ma se ho detto che ci pensavo io...” interloquì Pautasso che era appena entrato in cucina.”

Si guardarono e nessuno disse niente, neanche la pianta.

“Va bene, vediamo qui... Allora sei riuscito a fare il disegno che dicevamo. Vedi che non era poi così difficile?” Disse allegramente Mattia.

“Eh sì, caro cognato, questo disegno dell'altalena mi ha fatto penare un bel po', ma alla fine ho capito come dovevo fare”.

“Analemma, Oreste, analemma, non altalena. Va bene che è una parola greca....”

“Insomma, perché non lo chiamano “otto”... Io non capisco questa mania dei nomi stranieri.”

“In ogni caso il disegno va bene, ma come già avrai capito non è quello che corrisponde alla figura che hai costruito nel campo, perché questa tiene conto solo di una delle due cause, l'effetto della inclinazione dell'asse.”

“Quindi la faccenda non è chiusa?”

“Manca poco, Oreste, dobbiamo solo mettere insieme i risultati che abbiamo ottenuto fino ad ora.

Seguimi...”

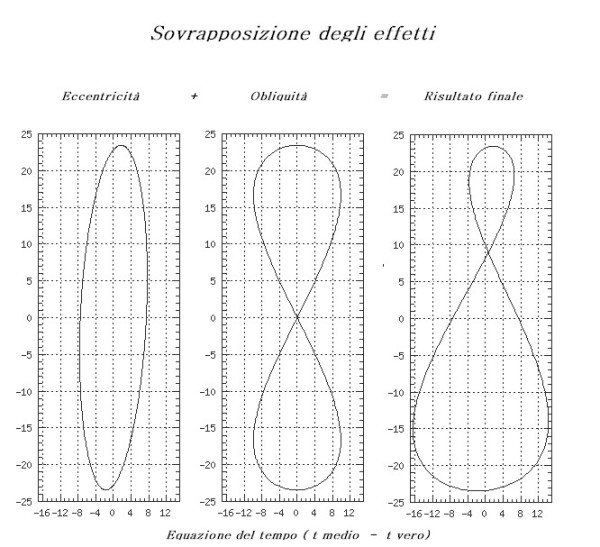
“Per un certo giorno conosciamo il valore dello scostamento dell'altezza del Sole al momento in cui passa al meridiano, rispetto alla linea dell'equatore celeste preso come riferimento. Quindi abbiamo la coordinata verticale.

Per determinare l'altra coordinata, quella orizzontale, basterà sommare gli effetti dei ritardi e degli anticipi causati da eccentricità e obliquità. Avremo così individuato il punto cercato sul nostro diagramma”

“Già, e ripetendo per i vari giorni questa operazione, troviamo gli altri punti...” Soggiunse pensieroso Pautasso.

“Ecco qui, riprese Mattia, vediamo… ad esempio, quando la declinazione è -20° rispetto alla linea dell'equatore celeste, l'effetto della eccentricità è di ritardare circa 5' e l'effetto della obliquità è di ritardare 9', quindi riporto sul diagramma complessivo 5+9=14 minuti di ritardo. Segniamo questi punti con un pallino rosso.

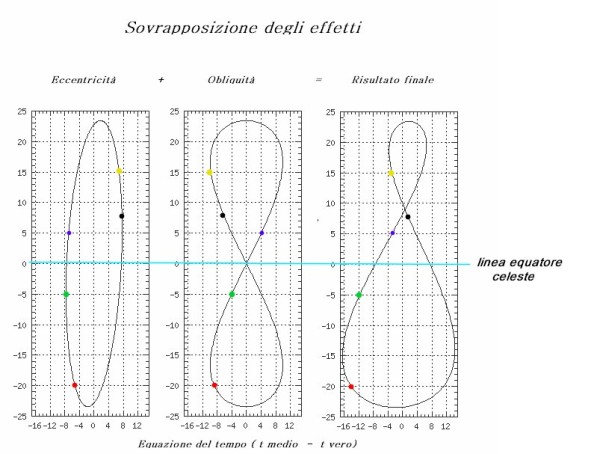
Ora saliamo lungo le curve fino ad un punto in cui la deviazione dalla linea dell'equatore sia, diciamo, -5°. L'eccentricità fa ritardare di 8' e l'obliquità di 4', totale 12' di ritardo. Questo lo vediamo osservando i pallini verdi. Con valori di declinazione al di sopra della linea dell'equatore, come +5° (e questo lo vediamo osservando i pallini blu) troviamo un ritardo di 7' per l'eccentricità e, questa volta, un anticipo per l'obliquità pari a 4'. Così il risultato complessivo sarà un ritardo di 3'.

Oltrepassato il punto di massima elevazione, le curve iniziano il tratto di ritorno, scendendo. Quando ripassano sulla linea a +15, vediamo i pallini colorati in giallo: per l'eccentricità ora abbiamo un anticipo di 7', mentre per l'obliquità abbiamo un ritardo di 10'. Conclusione: sovrapponendo i due effetti otteniamo il ritardo di 3'.

Ti faccio l'ultimo esempio, perché credo che a questo punto non avrai più dubbi... I pallini neri ci dicono che, quando le due curve scendendo, raggiungono l'elevazione + 8° sopra l'equatore, l'effetto della eccentricità è di causare un anticipo di 7' mentre l'effetto della obliquità è di causare un ritardo di 6'. Quindi l'effetto combinato è un ritardo di 2'.”

“Già! E ripetendo per i vari giorni questa operazione, troviamo gli altri punti...” Soggiunse pensieroso Pautasso “E quando li avremo individuati tutti, avremo disegnato l’ANALEMMA, ovvero quella curva geometrica a forma di otto allungato, che descrive la posizione del Sole nei diversi giorni dell'anno, alla stessa ora e nella stessa località.” Esclamò Mattia.

“Adesso ho proprio capito bene, Mattia, però, questo fatto del ciclo che si ripete due volte ad ogni giro non mi è del tutto chiaro... Se l'asse terrestre fosse verticale non ci sarebbe per niente questa oscillazione, ma se fosse orizzontale...?”

“Sai che c'è un pianeta che presenta proprio questa caratteristica? E' Urano, il penultimo pianeta del sistema solare, molto lontano, quasi 20 volte la distanza Terra-Sole. Come pensi che sarà il suo analemma? ”

Pautasso si concentrò, una ruga verticale apparve tra le sue sopracciglia.

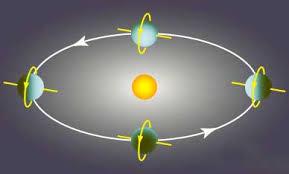
“Se l'asse del pianeta è parallelo al piano dell'orbita... quando si trova allineato con il Sole uno dei due poli è totalmente illuminato. I raggi lo colpiscono perpendicolarmente e dovrebbe fare molto caldo, in quel momento, invece all'equatore i raggi arrivano molto radenti. L'emisfero di quel polo sarebbe illuminato per 24 ore mentre nell'emisfero opposto sarebbe totalmente buio.”

“Bene, vai avanti, cosa succederebbe poi?”

“Dopo un po' di giorni l'asse non punta più verso il Sole e quel polo non riceve più i raggi proprio verticali come prima, l'emisfero non sarà più totalmente illuminato e il Sole, invece di occupare sempre lo stesso punto descriverà, nel corso delle 24 ore, un cerchio in alto nel cielo, piccolo se siamo al polo, più grande andando verso l'equatore. All'equatore i raggi saranno meno radenti e ci saranno 12 ore di luce e 12 ore di buio (anche se un po' di luce arriverà ancora finché il sole non è sceso troppo sotto l'orizzonte)”

“E nell'emisfero opposto?” incalzò Mattia visibilmente soddisfatto.

“Nell'emisfero opposto, vicino all'equatore, ci saranno 12 ore di luce con il sole basso sull'orizzonte, ma la luce andrà aumentando, man mano che il Sole salirà nei giorni successivi. A un certo punto il polo che prima era illuminato, comincerà ad essere in ombra qualche ora al giorno, finché, dopo avere percorso un quarto del cerchio dell'orbita, il Sole sarà perpendicolare all'equatore e i suoi raggi arriveranno radenti ai due poli. E' una situazione in cui tutti hanno 12 ore di luce e 12 ore di buio.”

Pautasso respirò profondamente.

“Perfetto, poi tutto si ripete simmetricamente nei tre mesi successivi, alla fine dei quali il polo che inizialmente era al buio si ritrova in piena luce. Negli altri sei mesi quindi la situazione si ribalterà.”

“Insomma, Mattia, ci sarebbero dei momenti di grandissimo caldo e dei momenti di grandissimo freddo, altro che stagioni e mezze stagioni... Ma a parte questo, come sarebbe l'analemma?”

“Ebbene, se la Terra avesse un asse inclinato di 90°, invece di avere questa oscillazione di 23,5°gradi in più o in meno nella declinazione, avremmo una oscillazione molto più ampia, di 90°, quindi tutta la volta visibile.

Per quanto riguarda gli anticipi e i ritardi, invece di 10 minuti, per effetto di questa estrema inclinazione, arriveremmo ad avere 39 minuti di ritardo o di anticipo del passaggio al meridiano.

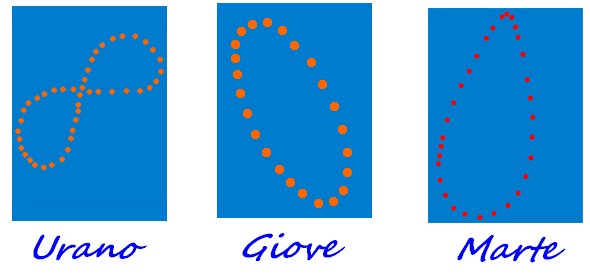
La curva formerebbe comunque un otto, di forma e proporzioni diverse, come accade del resto anche per Urano.”

“Quindi l'analemma è sempre una specie di otto? Per tutti i pianeti?”

“No, dipende da qual è l'effetto prevalente. Per esempio nel caso di Giove, che ha un'orbita più eccentrica della Terra e un asse di rotazione quasi perpendicolare al piano, prevale l'effetto della eccentricità e l'analemma ha la forma di un'ellisse...”

“Ancora un'altra ellisse... oh basta là!”

“Invece, nel caso di Marte, che ha un asse di rotazione inclinato poco più di quello terrestre, ma una eccentricità molto superiore, l'ellisse si restringe e assume la forma di una goccia, come fosse la parte inferiore dell'“otto”, senza l'anello superiore.”

“Bene! Adesso so proprio tutto...”

“Eh, Oreste, non farti illusioni, abbiamo solo sfiorato questo argomento, ci sarebbe ben altro da dire e da approfondire, ma diciamo che è già qualcosa. Adesso hai almeno un'idea del motivo per cui si forma quella strana figura, niente di più.”

“Si Mattia, ti devo proprio ringraziare. Sai cosa facciamo adesso? Diciamo a Sofia di preparare un buon caffè extra per tutti e poi spiego anche a lei questa cosa dell'analemma, scommetto che non ne sa niente.”

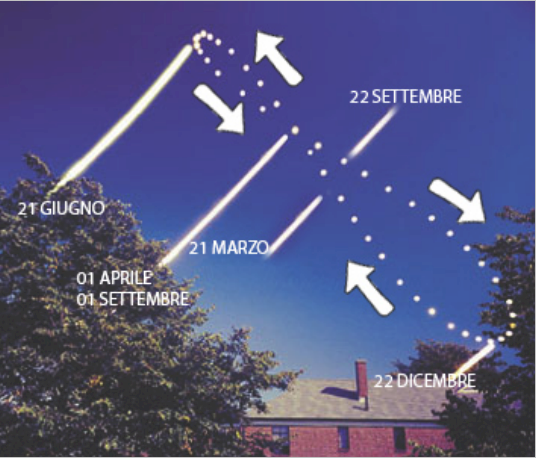
Qui sotto potete vedere immagini che abili fotografi hanno realizzato, con ammirevole costanza, sovrapponendo gli scatti eseguiti nel corso di un intero anno delle posizioni del sole.

L'ultima immagine è la simulazione di come apparirebbe l'analemma dalla superficie di Marte.

 

 

Cari lettori, a questo punto starete pensando che la storia è conclusa, vero?

Invece no, c'è ancora una piccola sorpresa che vi attende, come in quei film che poi salta fuori all'ultimo momento che l'assassino è un altro, che sembrava una brava persona.

Allora vi dico arrivederci nel backstage del teatro, non mancate nee?

 

QUI trovate gli altri articoli dedicati alla scoperta dell'analemma da parte di Oreste Pautasso

QUI potete trovare racconti di vario tipo dello stesso autore, Mauritius, insieme a quelli di Vin-Census