I nostri maghi hanno individuato la soluzione di questo quiz… ma io pensavo a qualcosa di più “rigoroso” e altrettanto semplice. Basta eseguire o anche solo immaginare di effettuare uno spostamento del triangolo superiore…

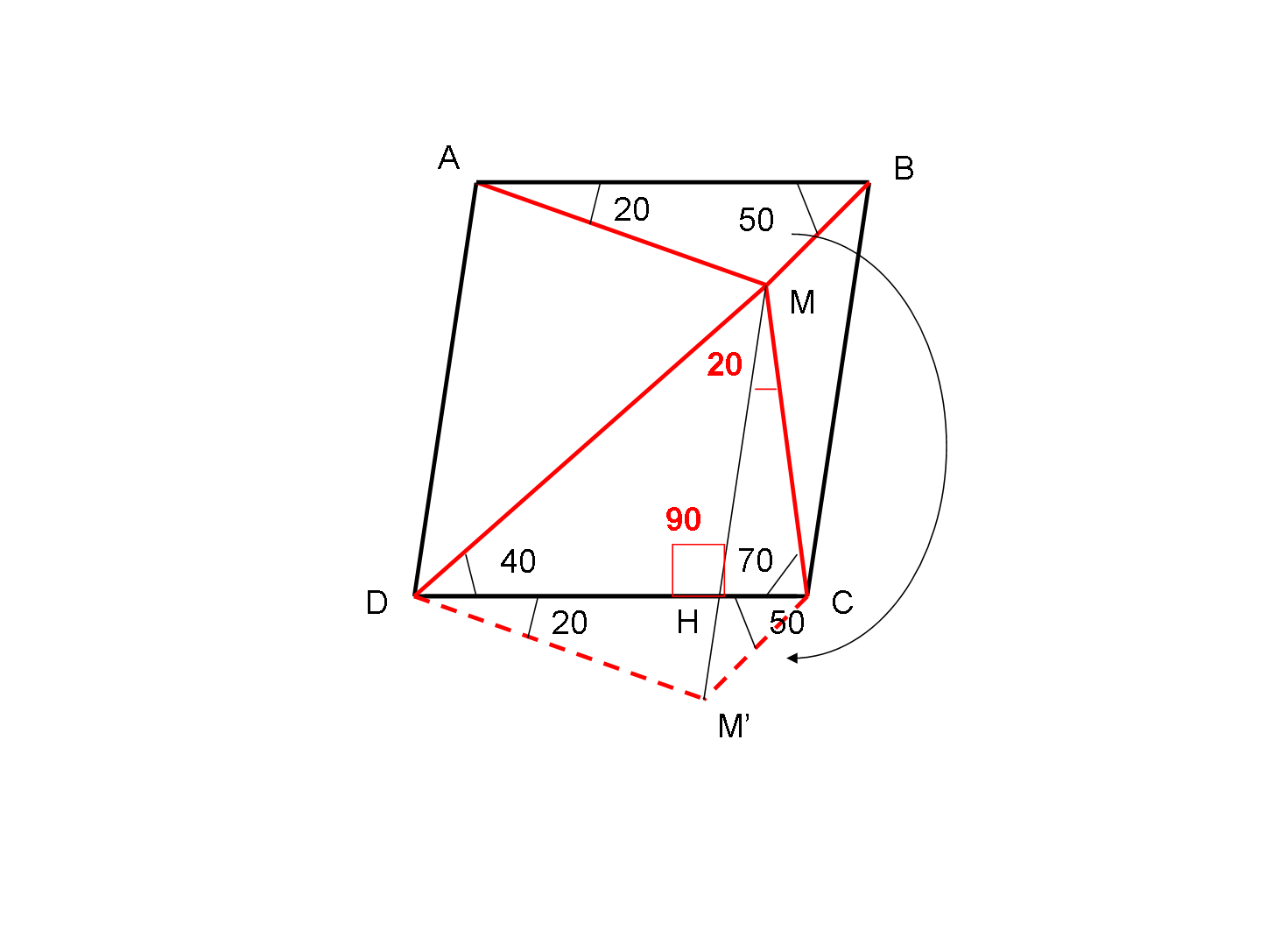
Il triangolo AMB può essere facilmente trascinato verso il basso in modo che AB coincida con CD (sono uguali per definizione). Si ottiene il quadrilatero MDM’C della figura che segue.

La somma degli angoli in D e C è uguale a 180°. Il che vuol dire che il quadrilatero CDMM' è inscrivibile in una circonferenza. Ne segue che la corda CM’ deve sottendere angoli alla circonferenza uguali. Ossia: M’DC = M’MC. Di conseguenza, dal triangolo MHC si ha che l’angolo MHC = 180 – 70 – 20 = 90. Tuttavia, l’angolo MHC è uguale all’angolo CDA  (angoli corrispondenti formati da AD e MM', tagliate dalla trasversale DC, paralleli perché lati del parallelogramma ADMM' ), da cui si ottiene che il parallelogramma di partenza deve essere un rettangolo!

QUI trovate tutti quiz del blog