Per una trattazione completa del viaggio verso il buco nero, si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Potrebbero bastare le immagini della prima parte… ma esse meritano di essere spiegate un po’ meglio. Oltretutto, dobbiamo anche dare una risposta al quiz sulla densità e la gravità (risolto brillantemente). Si notano facilmente cose abbastanza strane, ma molte altre, ugualmente interessanti, sono decisamente meno visibili. Andiamo, soprattutto, incontro a molte deformazioni subite dai raggi luminosi e l’idea che essi siano quanto di più rettilineo esista in Natura, è solo un lontano ricordo. La colpa di tutto ciò è sempre e soltanto della teoria della Relatività di Einstein che ha permesso la scoperta di questi oggetti, che rappresentano il confine tra realtà e assurdità.

Cerchiamo allora di analizzare nei dettagli quello che capita alla luce, ossia ai poveri fotoni e alle loro traiettorie quando passano vicino a un buco nero (QUI il viaggio di un fotone lanciato

E’ ben noto che quando la luce passa vicino a una massa enorme viene deviata sensibilmente rispetto alla sua direzione originale. E’ il fenomeno, più volte descritto, della lente gravitazionale. Lo stesso fenomeno che ci permette di vedere oggetti lontanissimi, teoricamente invisibili, che vengono ingranditi e resi osservabili quando si trovano dietro ad un oggetto molto massiccio che ne devia la luce e funge da lente. Ma vicino ad un buco nero le traiettorie si moltiplicano… In questo caso, la nostra astronave ci porterà così vicino a una massa enorme, con un campo gravitazionale talmente mostruoso, che tutto sarà veramente ai limiti del credibile.

Pensiamo per un attimo al nostro Sole. Esso sembra possedere una gravità enorme, tale da legare a sé pianeti e altri corpi minori fino a distanze grandissime. Eppure, un raggio di luce che lo sfiori, subirebbe uno spostamento di soli 1.75 secondi d’arco: un niente! La verità (ed è giusto ricordarla sempre) non sta tanto nella massa della nostra stella, ma nella sua densità. Se essa fosse compressa in un volume piccolissimo, anche il Sole renderebbe la vita molto dura a un fotone che si spingesse molto vicino alla sua superficie.  Non perché cambierebbe la gravità (la massa è la stessa), ma perché ci si potrebbe avvicinare molto di più alla sua superficie! (Vi siete mai chiesti cosa accadrebbe all'orbita della Terra se il Sole diventasse improvvisamente un buco nero? Niente di niente... non ci credete? Leggete QUI!)

In un oggetto “normale” è necessaria una contrazione di materia affinché essa ricada all'interno dell’orizzonte degli eventi che esiste teoricamente fin dall’inizio e che dipende solo dalla massa. Ne segue che questa operazione non può fare a meno di aumentare la densità. La densità è uguale alla massa divisa per il volume. Se la massa non cambia e il volume si rimpicciolisce, la densità deve aumentare. In linea puramente teorica, se il volume diventasse un punto senza dimensioni (singolarità), la densità diventerebbe infinita. Ma, come sappiamo, le singolarità non possono essere trattate con la relatività…

D’altra parte, però, se non ci fosse l’azione di contrazione di materia e la massa fosse incredibilmente alta, la distanza dell’orizzonte degli eventi, dipendendo solo dalla massa contenuta al suo interno, potrebbe essere molto grande. In altre parole, l’orizzonte degli eventi potrebbe essere esterno, fin da subito, all’oggetto considerato. Più massa c’è e più grande è il raggio della sfera in cui la luce sparirebbe per sempre. Stiamo parlando dei buchi neri galattici, con una massa pari a miliardi di volte quella del Sole. Essi avrebbero un orizzonte degli eventi lontanissimo dalla singolarità centrale. In altre parole la densità di ciò che sta dentro all’orizzonte sarebbe molto bassa, anche simile o minore di quella dell’acqua. L’ingresso di un astronauta nella zona del non ritorno non darebbe grandi problemi dato che la marea (che dipende dalla differenza tra due distanze rispetto a quella dal centro di massa) sarebbe insignificante…

Semplifichiamo ancora, attraverso la Fig. 13. In alto, abbiamo una stella qualsiasi, con una certa massa e un certo volume (e quindi una certa densità). Anch’essa ha il suo orizzonte degli eventi, che dipende solo dalla massa, ma esso cade all’interno della stella. E’ quindi impossibile risentire degli effetti limite che si verificano nei suoi pressi: sfiorare la superficie stellare vuole dire stare molto lontani dal limite del non ritorno.

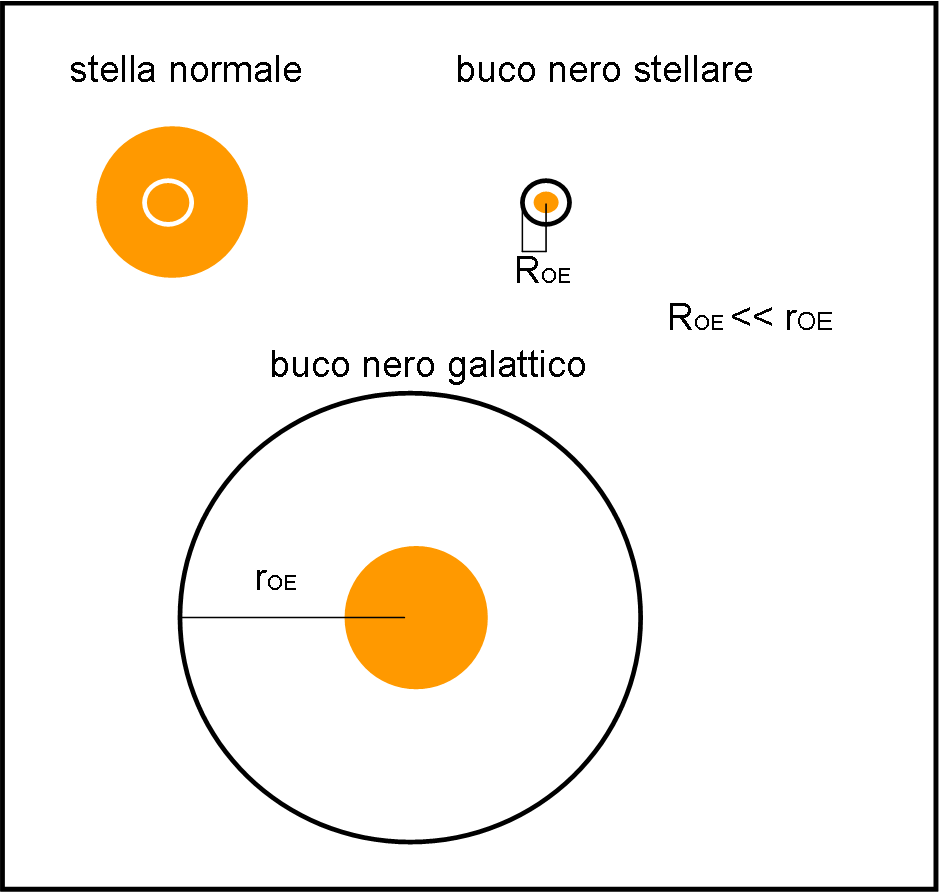
Se la stella si contrae, la sua massa (immaginiamo pure che rimanga perfettamente la stessa) si concentra in un volume sferico, il cui raggio è minore di quello dell’orizzonte degli eventi. E’ adesso possibile raggiungere quest’ultimo e subire tutti gli effetti del caso. Inoltre, la distanza dal centro di massa (o dell’ipotetico punto singolare) è molto piccola e quindi abbiamo anche un’accelerazione enorme, così come abbiamo descritto nella puntata precedente.

Facciamo attenzione: siamo spesso abituati a dire che l’accelerazione di gravità è costante (g), ma questo vale solo nei pressi del nostro pianeta (o di un qualsiasi altro), dato che le distanze in gioco sono piccole. In realtà, l’accelerazione varia in funzione dell’inverso della distanza al quadrato.

In basso, abbiamo invece un buco nero galattico. La sua massa è pari anche a miliardi di volte quella del Sole. Non sappiamo se occupi veramente un punto o sia distribuita all’interno del suo orizzonte degli eventi, ma quello che è sicuro è che il raggio di quest’ultimo è decisamente grande, dato che dipende solo dalla massa contenuta all’interno. Ne segue che la densità e l’accelerazione sono decisamente basse e così tutti gli effetti di tipo mareale.

La densità media di ciò che è contenuto all’interno dell’orizzonte deve essere molto bassa (comunque sia distribuita la massa), dato che a una massa enorme corrisponde un volume veramente spaventoso come dimensioni. Infatti, il raggio di Schwarzschild R_S (ossia dell’orizzonte degli eventi) di un buco nero aumenta linearmente con la massa, mentre il volume di un oggetto sferico, come l'orizzonte degli eventi, è proporzionale al cubo del suo raggio. Ne segue che  la densità del buco nero (inteso come tutto ciò che sta all’interno dell’orizzonte degli eventi) è inversamente proporzionale al quadrato della sua massa. Di conseguenza, la densità di un buco nero cala velocemente all'aumentare delle sue dimensioni, e quindi i buchi neri supermassicci hanno densità più basse di quelli più piccoli. Si potrebbero raggiungere densità addirittura inferiori a quella dell’acqua. Con poche formule altamente semplificate (ρ = densità) e ricordando che:

R_S = 2GM/c² = k M

ρ = M/V = M/(4πR_S³/3) = M/(hR_S³) = M/(hk³M³) = K/M²   (con h, k e K costanti)

Analogamente, l’accelerazione va con l’inverso della massa:

a = GM/R_S² = GM/(k²M²) = H/M   (con k e H costanti)

Vicinissimi all’orizzonte l’accelerazione di gravità potrebbe essere decisamente bassa. In via teorica, si potrebbe “entrare” in un buco nero con un’accelerazione di 1 g, ma sarebbe necessaria una massa pari a vari trilioni della massa solare, cosa non ancora riscontrata in Natura.

Questo è un discorso estremamente semplificato, dato che, varcata la soglia dell’orizzonte, tutto diventa ambiguo e misterioso. La stessa accelerazione non è ben definita in questa situazione limite e non potremmo certo applicare delle formule “classiche”. In ogni modo, ai confini dell’orizzonte, le deformazioni subite dalla luce rimangono le stesse di quelle che abbiamo visto la volta scorsa e che analizzeremo tra poco. L’unica consolazione è che superando l’orizzonte di un buco nero supermassiccio, gli effetti mareali sarebbero insignificanti e … non diventeremmo subito “spaghetti”! Ma quanto a tornare… è tutta un’altra cosa.

Riprendiamo, perciò, il viaggio verso il nostro buco nero stellare, in cui la densità è veramente spaventosa, dato che l’orizzonte degli eventi ha un raggio molto piccolo. Vale la pena ricordare che stiamo descrivendo un buco nero non rotante. Altrimenti dovremmo introdurre la rotazione dello spazio-tempo e tutto ciò che ne consegue (QUI).

Vediamo la situazione generale -e semplificata- utilizzando la Fig. 14.

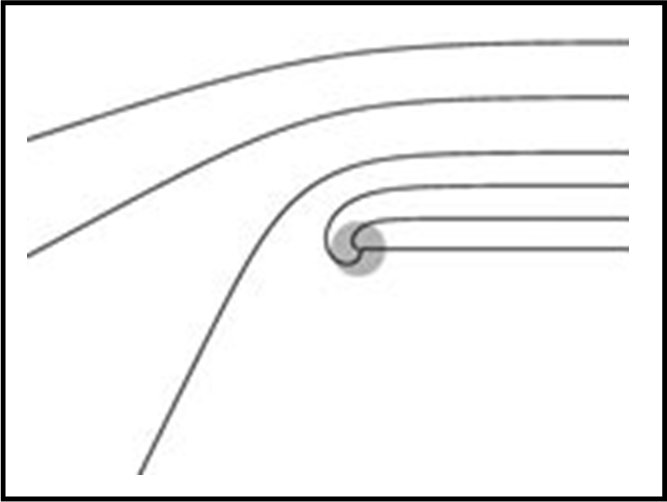
Il dischetto grigio rappresenta la regione all’interno dell’orizzonte degli eventi, quello che spesso viene identificato come buco nero, dimenticando che il buco nero reale risiede al suo interno e non ha alcun limite, fisicamente plausibile, al collasso. Tra parentesi, risulta chiara la differenza con altri oggetti degeneri. Nella nana bianca si ha uno stop al collasso dovuto agli elettroni, nella stella di neutroni questo primo “stop” è superato, ma entrano in ballo i neutroni (tutto ciò è perfettamente spiegato dal Principio di Esclusione di Pauli). Dopo di che non conosciamo, per adesso, nessun altro impedimento fisico al collasso gravitazionale.

Come ben noto a tutti, dall’orizzonte degli eventi niente (né materia né luce, che sono poi due facce della stessa medaglia) può uscire verso l’esterno. I tre raggi di luce più esterni sono deviati sempre di più a mano a mano che si avvicinano al buco nero, ma riescono a proseguire portando, però, un’informazione completamente falsata della loro provenienza originale. I tre raggi interni, invece, passano troppo vicino e vengono catturati: i fotoni attraversano l’orizzonte degli eventi e non possono più uscire terminando la loro vita all’interno della singolarità spazio-temporale (il buco nero, appunto).

Ovviamente la regione più interessante è quella al bordo dell’orizzonte degli eventi, proprio dove i fotoni riescono a salvarsi per un pelo o cadono dentro il cerchietto grigio. La Fig. 15 mostra, ad esempio, un fotone che fa tre quarti di giro attorno al buco nero e poi scappa in una direzione ben diversa da quella che avrebbe seguito senza la presenza del massiccio intruso.

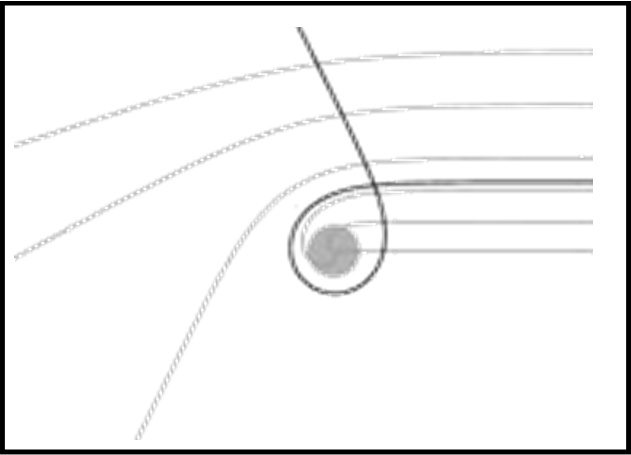
Non è più soltanto un effetto lente ma una specie di “roulette russa”: già non sappiamo dalla Meccanica Quantistica dove si trovi veramente un fotone e adesso ci si mette anche la “fionda” del buco nero a mandarlo in una direzione imprevedibile (sto scherzando, ovviamente!).

Nella Fig. 16, il fotone riesce addirittura a fare qualche orbita attorno al buco nero, per poi proseguire “quasi” indisturbato.

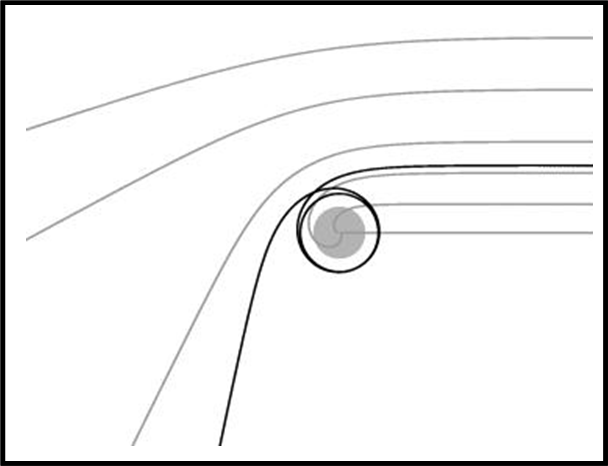
La Fig. 17 descrive, invece, la traiettoria di un fotone che, al termine dei suoi “giri”, viene catturato per sempre.

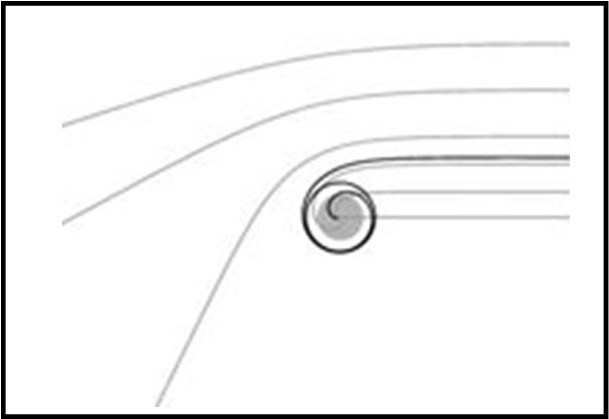
Il limite tra fotoni che scappano e fotoni che non riescono a scappare è una circonferenza con un raggio R pari a una volta e mezzo quello dell’orizzonte degli eventi (R_F/R_S = 1.5). Un fotone che descrivesse questa traiettoria girerebbe per sempre attorno al buco nero. Abbiamo trovato la SFERA FOTONICA. Accettate di prendere per buona la posizione esatta della sfera fotonica, dato che per ricavarla sarebbe necessario introdurre la metrica di Schwarzschild e non è cosa per noi…

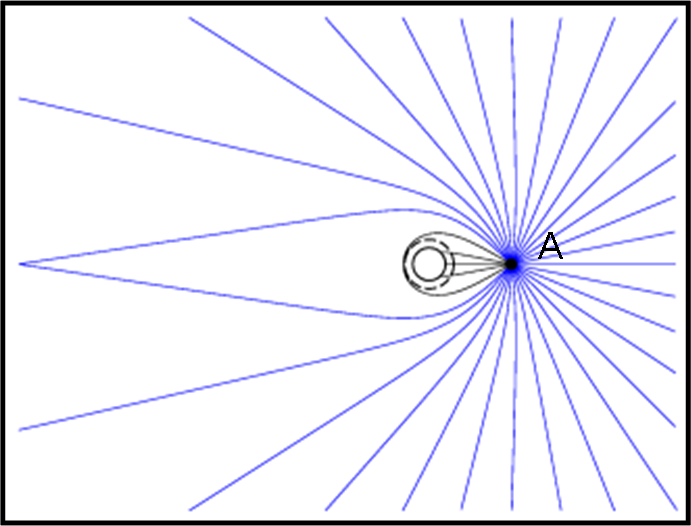
Torniamo un poco indietro nel nostro viaggio e analizziamo meglio cosa si vede e cosa succede quando si è, ad esempio, a 600 km dall’orizzonte degli eventi. Riportiamo l’immagine in Fig. 18.

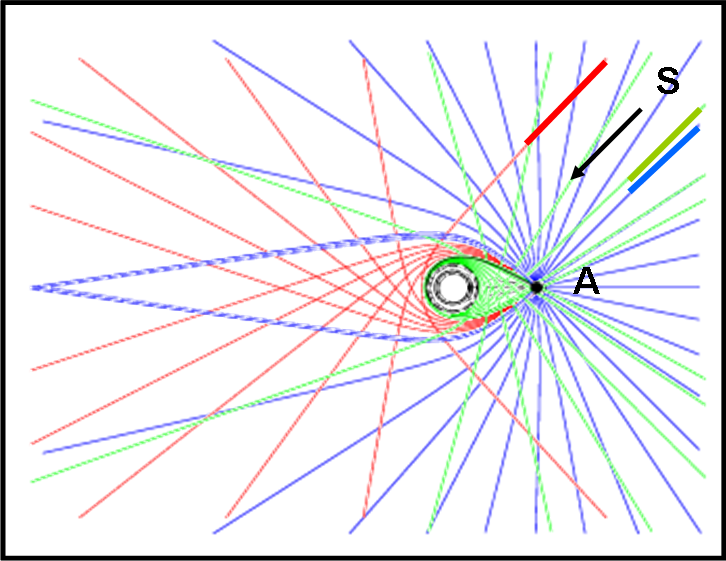
L’astronave è rappresentata nella Fig. 19 dal punto nero A sulla destra. L’orizzonte degli eventi (OE) è la circonferenza a linea continua, mentre quella a trattini corrisponde alla traiettoria del fotone che rimane per sempre in orbita (con raggio R uguale a 1.5 R_S).

L’astronave riceve la luce da tutte le direzioni, ma…

Quella che proviene “direttamente” all’astronave dalla metà del cielo nella parte alta della figura è rappresentata dalle linee nere e viene parzialmente deformata quando passa troppo vicina al buco nero (ci saranno linee uguali anche nella parte bassa, ma non le indichiamo per non “caricare” troppo la figura). Arriva, però, anche luce che percorre le linee rosse (questa volta, per semplicità, abbiamo disegnato solo quelle della parte bassa del cielo, ma lo stesso capita nella parte alta). Questi fasci di fotoni sono catturati dalla gravità dell’enorme intruso e sono rimandati indietro. La linea blu è invece un raggio che proviene nuovamente dalla parte alta, ma viene fatto circolare completamente e arriva all’astronave come se provenisse da una direzione ben diversa.

Soffermiamoci solo un attimo sulle due traiettorie che provengono da S e da R. La luce della stella S si vede sicuramente due volte: una provenendo da dietro (linea nera) e un’altra dopo aver percorso un giro attorno al buco nero con la direzione apparente AS’.  Analogamente, la stella R si vede perfettamente sia dietro all’astronave (linea diretta), sia davanti.

La situazione, tuttavia, può dar luogo a infinite possibilità, dato che i fotoni possono girare attorno al buco nero in qualsiasi modo e uscire quando vogliono (o possono). In poche parole, attorno al buco nero si creano infinite immagini multiple. Noi abbiamo tentato una semplice rappresentazione  su un solo piano, ma la realtà è tridimensionale. Ed ecco che si cominciano a intuire benissimo quei cerchi che si formano attorno al buco nero vero e proprio.

Capito il meccanismo in modo un po’ disordinato, vediamo di analizzare la situazione con maggiore ordine e facendo un passo alla volta.

Nella Fig. 20 consideriamo soltanto le immagini “dirette”, ossia quelle che corrispondono a raggi luminosi che giungono all’astronave senza compiere giri attorno all’orizzonte degli eventi (o alla sfera fotonica).

Essi sono, comunque piegati a causa della gravità del buco nero e ci permettono di vedere anche ciò che sta esattamente dietro il buco nero (il classico effetto lente). Ad esempio, se in quella posizione vi fosse una nube molecolare, essa verrebbe vista come un disco (anello di Einstein) tutt’attorno al buco nero. Immaginiamo che sia l’anello violetto che si identifica molto bene nell’immagine ripresa dall’astronave.

Tutti gli altri raggi luminosi provenienti dal cielo subiranno deformazioni sempre minori a mano a mano che si allontanano dall’orizzonte degli eventi. In poche parole, si vede tutto il cielo e un anello che caratterizza ciò che sta dietro al buco nero. In particolare, la deformazione è localizzata molto vicina al buco nero, mentre il resto del cielo sembra quasi normale.

Focalizziamo allora l’interesse all’interno dell’anello che circonda il buco nero. Analizziamo la Fig. 21, dove i raggi rossi provengono da tutte le direzioni, ma prima di giungere all’astronave, essi fanno un “giro di boa” attorno alla sfera fotonica.

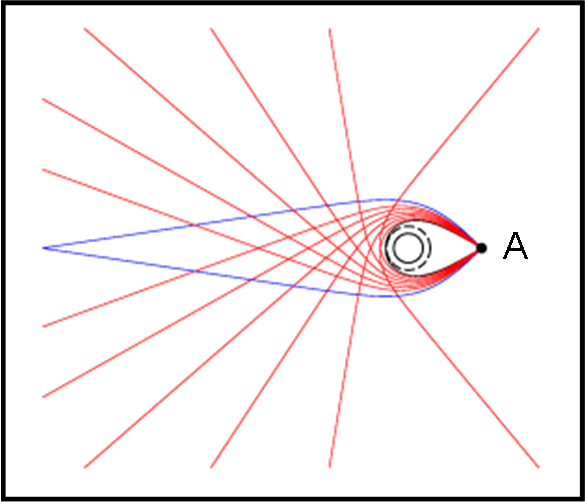
Ancora una volta si vede tutto il cielo, ma la sua luce si concentra SOLO all’interno dell’anello definito precedentemente. In poche parole, i raggi rossi creano una seconda immagine del cielo, invertita e profondamente distorta, posta all’interno dell’anello causato dai raggi blu diretti.

Possiamo anche proseguire, considerando i raggi verdi di Fig. 22.

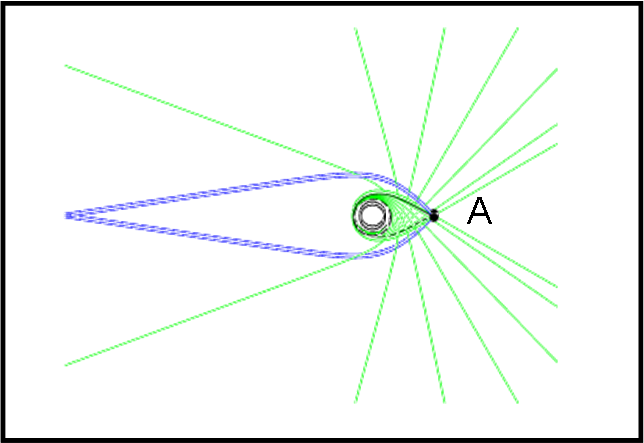
Questi passano ancora più vicini alla sfera fotonica (addirittura tra lei e l’astronave). Provengono nuovamente da tutto il cielo, localizzandosi, però, all’interno di un anello ancora più vicino al buco nero.

Volendo, potremmo proseguire per un numero infinito di volte, andando sempre più vicini. Direi che non è difficile concludere che tra il primo anello e il buco nero si creano infiniti anelli che contengono infinite immagini di tutto il cielo. Ricordiamo, infatti, che ciò che vediamo in un piano avviene per tutti gli altri piani e i punti si trasformano in anelli.

Combiniamo le tre serie di raggi una sola figura (Fig. 23).

A parte l’apparente caos (che ormai non ci spaventa più) notiamo benissimo che da una certa stella S provengono tre raggi di colore diverso (sono paralleli tra loro…) che danno immagini distinte nei pressi del buco nero.

Guardando attentamente la Fig. 18, potremmo divertirci a trovare i vari anelli concentrici e contare quante volte stiamo vedendo il cielo nella sua completezza. Sto scherzando, ovviamente, dato che il caos sembra regnare completo, anche se il tutto segue delle regole perfettamente dettate dalla relatività generale.

Fermiamoci qui per dare tempo di assimilare al meglio la parte “teorica” e la parte “pratica”, rappresentata dalle bellissime simulazioni. Avvicinandoci ancora alla sfera fotonica le cose si complicheranno e sarà bene avere le idee molto chiare su questa prima parte del viaggio.

Roba da far girare la testa! E, forse, gli astronauti lo fanno veramente per tornare a una visione ancora normale… ma non lo sarà per molto.

 

QUI la serie completa degli articoli dedicati al viaggio verso il buco nero.

A proposito di fotoni e dei loro viaggi, QUI potete farvene raccontare uno molto avventuroso vissuto da un fotone prodotto da un fascio di raggi gamma provenienti da un lontanissimo nucleo galattico attivo: vivrete, come una fiaba, un viaggio lungo circa di sette miliardi e mezzo di anni e comprenderete come, grazie ad esso, si sia riusciti ad ottenere informazioni fondamentali sulla storia dell’Universo e su ciò che lo permea