Quiz: L'isola che non c'è.***

26/05/17

Quiz: L'isola che non c'è.***

Categorie: Matematica Tags: Scritto da: Club dei Maghi Commenti:15

 

Il Mont-Saint-Michel ha le più alte maree sizigiali dell'Europa Continentale, è uno spettacolo indimenticabile!

Con la bassa marea il mare è a 15km dalla costa. La marea arriva alla velocità di un cavallo al galoppo, con il livello del mare in aumento di 15 metri tra bassa e alta marea

 

Video      La marea a Mont-Saint-Michel

 

 

Un modo per rappresentare il fenomeno del “distacco” del monte dalla costa, nel momento in cui la marea si innalza, può essere quello di assimilare la variazione del profilo dell'istmo fino alla scomparsa del lembo di terra che unisce l'isola alla costa, al tracciato di una curva ellittica in cui,  progressivamente, vengono modificati alcuni dei coefficienti presenti nella equazione

curva ellittica

L'equazione delle curve ellittiche, che abbiamo presentato in precedenti quiz, ha la seguente forma generale:

y2=x3+ax +b

 

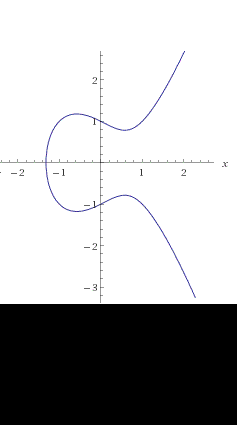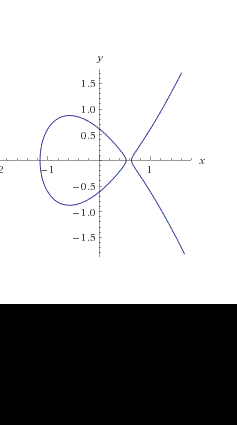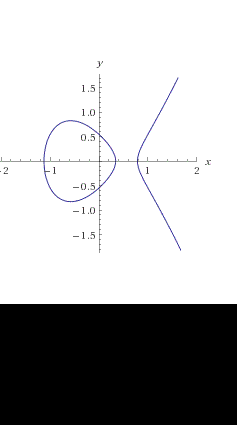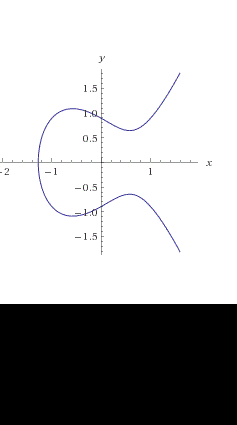
Per determinati valori di “a” e di “b”  la curva sarà costituita da un solo ramo (figura di sinistra), per altri valori ci saranno invece due rami distinti, cioè si formerà una “isola” (figura di destra).

C'è una relazione fra i coefficienti a , b dell'equazione della curva ellittica che ci dice quando la curva avrà una delle due forme?

Il problema non è dei più semplici, e fra l'altro non viene contemplato nello studio delle ellittiche.

A chi desidera un aiuto per risolvere il quiz suggeriamo di  evidenziare con il cursore  le righe seguenti da “inizio” a “fine” .

INIZIO suggerimenti

1) Notiamo subito che nel grafico di sinistra la curva interseca l'asse x (y=0) in un punto, mentre nel grafico di destra in tre punti distinti; ci chiediamo quando questo succeda.

2) Studiare gli zeri della curva equivale a studiare gli zeri del polinomio f(x)= x3 +ax +b=0  notare innanzitutto che tale equazione ha almeno una soluzione.

3) Si tratta ora di cercare quando ci sono tre soluzioni; ciò accade quando la funzione polinomiale

f(x)=x3+ax +b

interseca l'asse delle x in tre punti distinti. Si tratta dunque di studiare la funzione con i metodi consueti dell'analisi; che relazione deve esserci fra i coefficienti a,b affinché si abbiano tre soluzioni distinte?

FINE suggerimenti

isola ellittica (1)

 

 

Il quiz presuppone la conoscenza dei massimi e dei minimi relativi di una funzione. Chiaramente il quiz è aperto a tutti, fuorché a chi scrive. Il quiz è nato da un commento sulla geometria proiettiva e le curve ellittiche (qui il commento) dove Maurizio aveva sollevato questa importantissima osservazione.

E' ovvio che non siete obbligati a seguire la strada consigliata, ci possono essere chiaramente altri modi per dimostrarlo direttamente. Ciascuno segua il ragionamento che più gli aggrada.

 

QUI la soluzione

 

QUI tutti i quiz pubblicati nel circolo e QUI gli altri quiz del Club dei Maghi

 

Articoli correlati

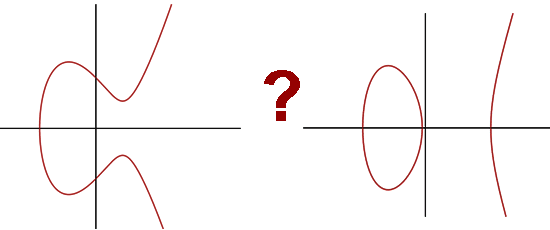
15 commenti

  1. oreste pautasso
    27/05/2017 at 10:09

    Una osservazione che potrebbe essere utile ...

    Guardando l'animazione sembrerebbe che, prima della separazione in due rami, la curva vada stringendosi sempre più, in corrispondenza di un preciso valore di x, a cui  nel semipiano positivo della y corrisponde un valore di minimo relativo e, nel semipiano negativo della y, un valore di massimo relativo.

     

  2. Vincenzo Zappalà
    27/05/2017 at 11:31

    Occhio anche alla cuspide!!! :mrgreen:

  3. Club dei Maghi
    27/05/2017 at 13:43

    coraggio, non abbiamo trovato nella letteratura considerazioni su questo fatto. Forse stiamo analizzando  qualcosa di nuovo.!

  4. Vincenzo Zappalà
    27/05/2017 at 14:47

    Non voglio rompere le scatole... ma se si calcola il discriminante dell'equazione, si trova quando c'è un punto singolare (o, meglio, imponendo un punto singolare si dovrebbe trovare il discriminante che va a zero). Se, invece, il discriminante è maggiore di zero ..... ecc., ecc...

    ma mi fermo qui... aspettando i disegni della ciliegia di Pippo e Pappo :-P

  5. Club dei Maghi
    27/05/2017 at 16:46

    l intuito ê proprio la base per qualsiasi affermazione scientifica..

  6. maurizio bernardi
    28/05/2017 at 12:18

    Propongo questo inizio di soluzione a cui, in un prossimo commento, aggiungerò la parte conclusiva.

    Per chi desidera poterlo vedere è sufficiente selezionare il blocco di testo "invisibile" che segue...

    da QUI

    L'equazione di partenza è: y2 = x3 + ax + b

    ricavo y= √ (x3+ax+b)  considero solo la radice positiva (parte superiore del grafico).

    Calcolo la derivata prima di y. Quando è nulla ho un punto min o max

    la y' ha un numeratore = 3x2 + a   ponendolo = 0 ottengo 3x2 = -a

    da cui ricavo la x per la quale ho min o max

    x = √ (-a/3) anche qui considero solo la x positiva .

    Noto che per avere valori di x reali, il coefficiente “a” deve essere negativo.

    Ora sostituisco nella espressione di y il valore di x che ho trovato

    y=√ ( √(-a/3)3 + a √(-a/3) +b)

    nel punto x= √(-a/3) ho il valore minimo di y. Ponendo questo minimo = 0 ho il punto di singolarita che discrimina i casi in cui la curva ha un solo ramo dal caso in cui ne presenta due.

    In questo punto angoloso la funzione è continua ma non derivabile. A sinistra la derivata ha segno negativo, a destra ha segno positivo. Il punto è comunque un minimo relativo.   

    Fino a QUI

    Si tratta ora di proseguire il ragionamento per arrivare a trovare la relazione tra i coefficienti a e b  con cui rispondere al quesito....

    Attenzione: non è l'unico modo di procedere.  Ci sono interessanti strade alternative che potrete scoprire...

     

     

     

  7. Club dei Maghi
    29/05/2017 at 06:40

     

  8. Club dei Maghi
    29/05/2017 at 20:56

    Tra gli oltre 160 lettori che hanno letto il testo del quiz ci sarà certo quella decina di affezionati solutori che hanno partecipato alle ultime discussioni delle soluzioni.

    Siamo fiduciosi che non si lasceranno sfuggire l'occasione di dire la loro anche questa volta. La marea non è una cosa che si possa ignorare...

    Fatevi avanti dunque, senza spingere....:wink: :mrgreen:

  9. Club dei Maghi
    30/05/2017 at 13:11

    sembra difficile..in realtà si può fare. In fin dei conti la curva si annulla dove si annulla un polinomio di terzo grado . La derivata  é un polinomio di secondo grado , quindi é possibile studiarne il segno..si tratta di impostare una disequazione..

  10. Fabrizio
    30/05/2017 at 18:18

    Quando si forma l'isola il grafico interseca 3 volte l'asse delle x, mentre quando ha forma di penisola interseca una sola volta l'asse delle x.

    Quindi l'equazione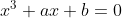 x^3+ax+b=0 (avendo posto y=0 per trovare l'intersezione con l'asse x) in un caso deve essere soddisfatta per 3 valori reali diversi di x, nell'altro per un solo valore reale di x.

    Una via per trovare quale è la relazione tra a e b che fa cadere l'equazione in uno o l'altro caso potrebbe essere questa.

    Riscrivo l'equazione in questo modo: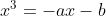 x^3=-ax-b.
    Il grafico del termine a destra è una retta di pendenza -a passante per il punto (0,-b).  A sinistra c'è una cubica passante per l'origine. Cercare le intersezioni della nostra curva ellittica con l'asse x è equivalente a cercare le intersezioni di queste due curve.

    Per aiutarmi nel ragionamento faccio un grafico di queste curve per un valore definito di a e faccio variare il valore di b.

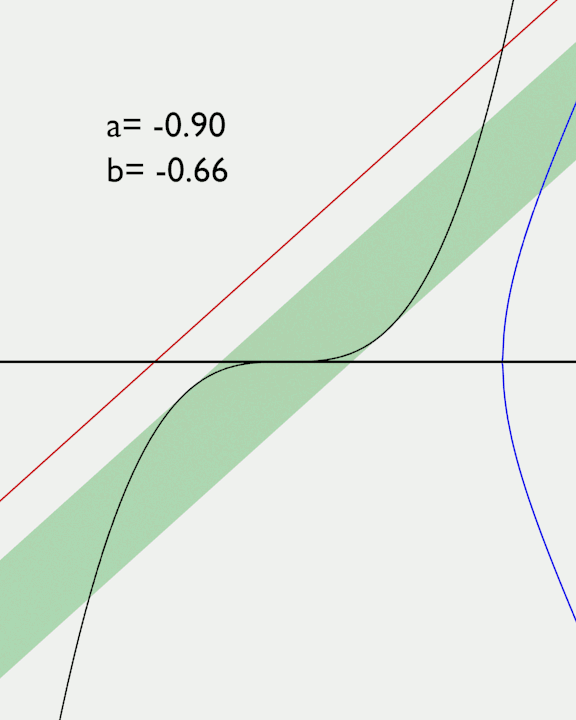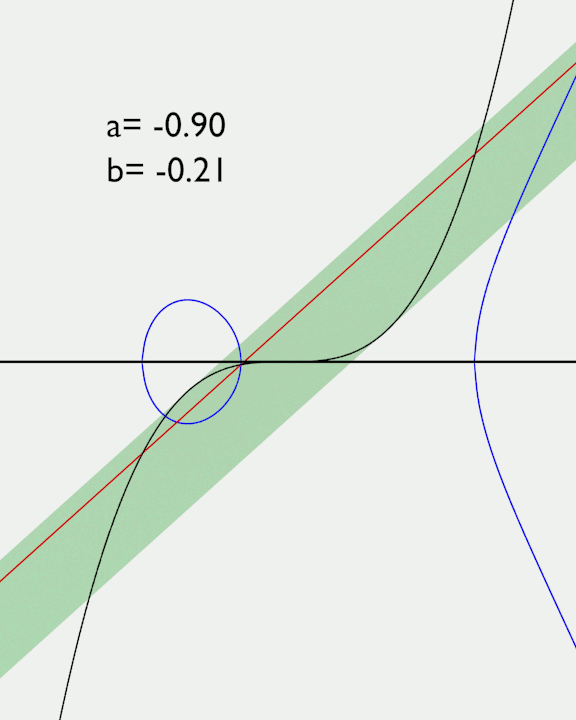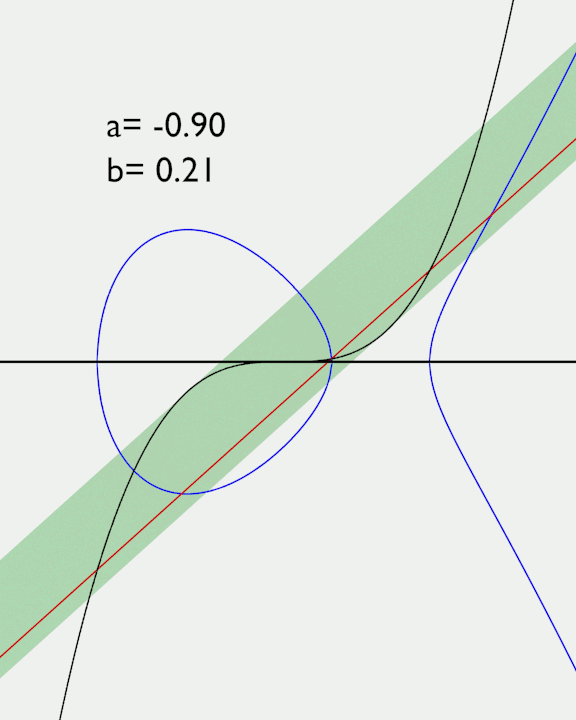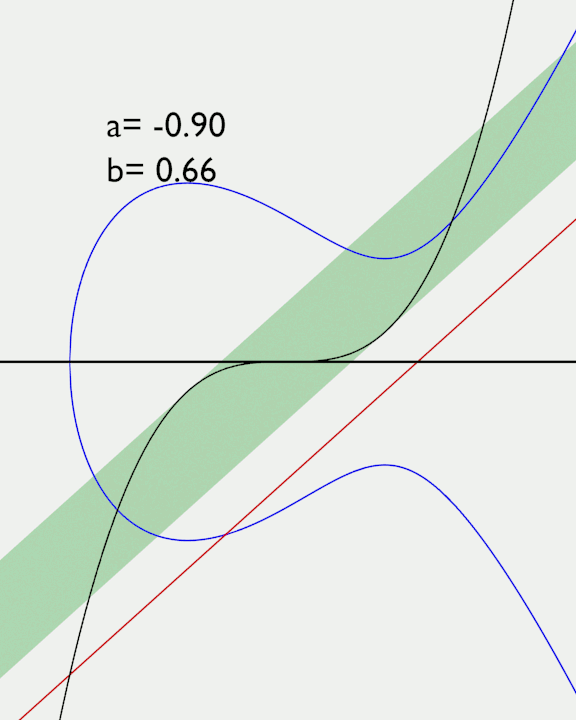
    Posso vedere che se il valore di b è tale da porre la retta a destra o sinistra della fascia verde, la curva ellittica interseca l'asse delle x in un solo punto.

    Se invece il valore di b inserisce la retta all'interno della fascia verde, allora  la curva ellittica interseca l'asse delle x in 3 punti. Cioè si crea l'isola.

    I limiti della fascia verde sono le rette tangenti alla cubica, dove due punti di intersezione collassano in un solo punto prima di scomparire. In questi punti la pendenza della retta e della cubica devono essere uguali. La pendenza di una curva è data dalla derivata prima della sua equazione. Allora

    \small \frac{\mathrm{d} x^3}{\mathrm{d} x} =\frac{\mathrm{d} }{\mathrm{d} x}(-ax-b)\;,\; \; \; \; \; 3x^2=-a \;,\; \; \; \; \; {\color{Blue} x = \pm \sqrt{\frac{-a}{3}}}

    Questi sono i valori di x per i quali la retta deve essere tangente alla cubica. Intanto si vede che a deve essere negativa affinché possano esistere questi punti. Con a positiva non c'è l'isola qualsiasi sia il valore di b. Il grafico aiuta a vedere questo fatto poiché è evidente che una rette che scendesse verso destra (a>0) incontrerebbe la cubica in un solo punto.

    A questo punto per trovare i valori di b che definiscono le due rette limite della fascia verde impongo che retta e cubica effettivamente si incontrino nel punto di tangenza:

    \small x^3=-ax-b \; \;\;dove\, sostituisco\; x=\pm \sqrt{\frac{-a}{3}} \\ \left (\pm \sqrt\frac{-a}{3} \right )^{3}=-a\left (\pm \sqrt\frac{-a}{3} \right )-b

    ora seguono alcuni passaggi per trovare b in funzione di a

    \small b=-a\left (\pm \sqrt\frac{-a}{3} \right )-\left (\pm \sqrt\frac{-a}{3} \right )^{3} \\ b=\mp \sqrt\frac{-a}{3}\left ( a+\left ( \sqrt\frac{-a}{3} \right )^2 \right )\\ b=\mp \sqrt\frac{-a}{3}\left ( a-\frac{a}{3} \right )\\ {\color{Blue} b=\mp \frac{2\,a}{3}\sqrt\frac{-a}{3}}

    questa relazione definisce i limiti della fascia verde.

    Quindi l'isola esiste se sono soddisfatte queste due condizioni:

    {\color{Blue} \begin{cases} & a<0 \\ & \frac{2a}{3} \sqrt{\frac{-a}{3}}<b<-\frac{2a}{3} \sqrt{\frac{-a}{3}} \end{cases}}

  11. Vincenzo Zappalà
    30/05/2017 at 18:41

    Bene, bene... vedo che tutto il lavoro viene fatto per trovare in un modo o nell'altro il discriminante dell'equazione . Ovviamente dato quello si ha la relazione tra a e b per passare da un caso all'altro attraverso il valore zero e quello di valore zero con a = o. Veramente bello vedere come girando attorno si arriva sempre a un'unica relazione... Evviva l'isola che non c'è!!!! :mrgreen:

  12. Club dei Maghi
    31/05/2017 at 06:45

    si, tutto gira attorno al discriminante dell'equazione, ovvero al nodo.

    Ottimo lavoro fabrizio, diverso anche dalle nostre soluzioni.Comunque aspettiamo anche gli altri, che magari trovano un modo ancora diverso. Comunque il quiz resterà aperto fino a sabato, poi la soluzione

  13. maurizio bernardi
    31/05/2017 at 09:09

    Complimenti a Fabrizio per la soluzione davvero elegante.

    Come promesso nel  mio precedente commento, concludo la pubblicazione della soluzione di cui avevo fornito (mascherata) la prima parte.  Ecco il testo completo in chiaro:

    L'equazione di partenza è: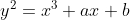     y^2=x^3+ax+b

    ricavo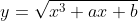 y=\sqrt{x^3+ax+b}      considero solo la radice positiva (parte superiore del grafico).

    Calcolo la derivata prima di y. Quando è nulla ho un punto min o max

    La derivata  y' ha un numeratore =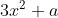 3x^2 +a     ponendolo = 0   ottengo  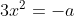   3x^2=-a    da cui ricavo la x per la quale ho  y   min o max

    x=\sqrt{-a/3}    anche qui considero solo la x positiva .

    Noto che per avere valori di x reali, il coefficiente “a” deve essere negativo.

    Ora sostituisco nella espressione di y il valore di x che ho trovato

    y=\sqrt{(\sqrt{(-a/3)^3}+a\sqrt{-a/3}+b)}

    nel punto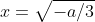   x=\sqrt{-a/3}   ho il valore minimo di y. Ponendo questo minimo = 0 ho il punto di singolarità che discrimina i casi in cui la curva ha un solo ramo dai casi in cui ne presenta due. In questo punto angoloso la funzione è continua ma non derivabile. A sinistra la derivata ha segno negativo, a destra ha segno positivo. Il punto è comunque un minimo relativo.

     

    Ricavo il valore di b che azzera y (caso della singolarità)

    -b=\sqrt{(-a/3)^3} + a\sqrt{-a/3}

    -b=\sqrt{-a/3)} (-a/3+a) =a(2/3)\sqrt{-a/3}

    b^2= 4a^2/9 (-a/3) = -a^3 4/27

    Ad esempio: se a=-1

    b=-2(-1)/3 \sqrt{1/3} = 2/3 \sqrt{1/3} = 0,3849

    Se b è maggiore del valore così calcolato avrò y reale e >0 (un solo ramo),

    se b è minore avrò y immaginario in quel punto e due rami separati.

    In conclusione la relazione cercata, tra a e b, è la seguente:

    b^2=a^3(-4/27)      o, in altra forma:       (b/2)^2=-(a/3)^3

  14. Fabrizio
    02/06/2017 at 23:06

    Guardando il grafico ho pensato ad un modo diverso per trovare la relazione tra a e b.

    Se penso al parametro b che appare nella equazione come una variabile, posso ottenere un grafico come quello in figura. La curva in rosso unisce i punti dove si annulla y. Per avere 3 punti dove si annulla y occorre che b sia compreso tra il massimo ed il minimo relativo della curva.

    Sembrerebbe un metodo completamente diverso da quello che ho utilizzato nella risposta precedente. Ovviamente si ottiene lo stesso risultato. Curiosamente però, il procedimento algebrico è molto simile nei due metodi.

    Equazione della curva rossa: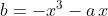   b=-x^3-a\,x

    Minimi/massimi della curva: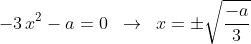 -3\,x^2-a=0\;\;\rightarrow \;\;x=\pm \sqrt{\frac{-a}{3}}

    Valori di b al minimo/massimo: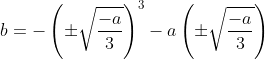 b=-\left ( \pm \sqrt{\frac{-a}{3}} \right )^3-a\left ( \pm \sqrt{\frac{-a}{3}} \right )

    Sono quasi gli stessi passaggio algebrici del metodo della mia prima risposta anche se qui sono applicati ad un grafico totalmente diverso.

  15. Club dei Maghi
    03/06/2017 at 07:10

    si, questo metodo si avvicina di più a quello che abbiamo usato noi, anche se mi  sembra sia ancora leggermente diverso

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.