Categorie: Fisica classica
Tags: geometria grafico Pappo Peppa Pippo quiz sistemi di riferimento
Scritto da: Vincenzo Zappalà
Commenti:17
QUIZ: niente torta per Pippo e Pappo, solo ciliegie… */**
Pappo e Pippo a furia di mangiar torte si sono “beccati” una terribile gastroenterite. Conclusione? Mai più dolci per loro e per il dopo pranzo solo e soltanto frutta. Ovviamente, due menti vulcaniche come le loro hanno subito escogitato un gioco fuori dal normale per rimanere nei limiti della dieta impostagli dal medico.
N.B.: I maghi hanno presentato un bellissimo quiz di una certa difficoltà e noi, invece, ne presentiamo uno per tutti (loro, se lo vorranno, si muoveranno solo dopo un po’).
Pappo sale su una piattaforma girevole P, mentre Pippo sta fuori di essa con le ciliegie, private del nocciolo. La situazione è quella di Fig. 1. All’inizio, la piattaforma è immobile e Pippo lancia direttamente le ciliegie verso Pappo che deve prenderle con la bocca. Dopo molti esercizi, i due fratelli sono ormai diventati dei veri campioni, sia nel lanciare che nel ricevere.
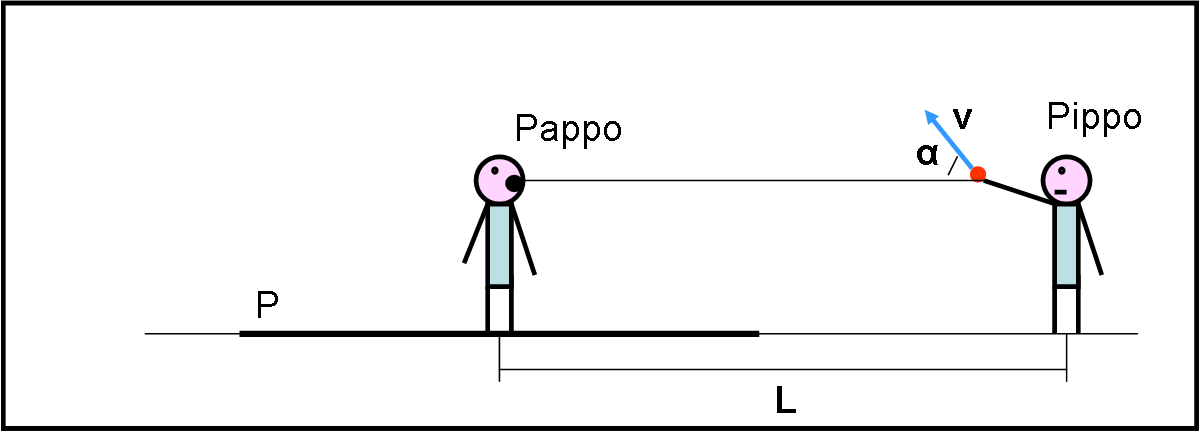
Vediamo le condizioni del gioco. Pippo lancia le ciliegie con una velocità v, che forma un certo angolo α con la linea orizzontale che unisce mano di Pippo e bocca di Pappo. La velocità è contenuta nel piano verticale rispetto al suolo e la traiettoria è studiata in modo che il punto finale sia proprio la bocca di Pappo. La distanza tra i due fratelli è L.
Nel frattempo, è sopraggiunta Peppa, la sorella minore, che è un piccolo genio in geometria, ma che ancora non ha studiato la fisica a scuola e quindi ragiona in modo molto empirico, ma veramente brillante. Conosce solo la forza di gravità, un poco di scomposizione di vettori e si azzarda a calcolare il seno e coseno di un angolo. Ma poco di più…
I fratelli le chiedono di DISEGNARE la traiettoria della ciliegia, vista sia nel sistema di riferimento di Pippo sia in quello di Pappo. Peppa si sente presa un po’ in giro e risolve immediatamente il problemino sia visto nel piano verticale che in quello orizzontale (ossia in quello della figura e in quello perpendicolare (visione dall’alto)) consegnando i quattro disegni veramente banali. Ovviamente dovete farlo anche voi!
Abbastanza offesa chiede ai due ragazzi di complicare un po’ la faccenda in modo da poter dimostrare la sua capacità grafica.
Pippo e Pappo confabulano a lungo e poi prendono la decisione con un bel sogghigno sul volto. L’ha voluto più difficile? e tale l’avrà!
Pappo torna sulla piattaforma girevole e, questa volta, la mette in moto con una velocità angolare costante ω. La velocità è tale che Pappo eseguirà due volte un giro completo prima di ripresentarsi frontalmente a Pippo, dopo un tempo τ, tale che la ciliegia arrivi esattamente nella bocca di Pippo. La velocità di lancio rimane esattamente la stessa della volta precedente (Fig. 2).
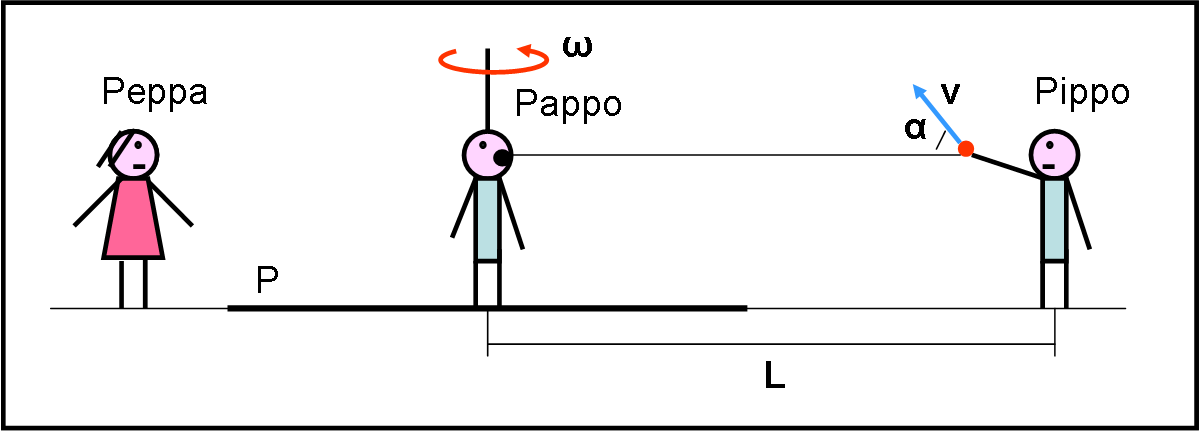
Per dare a Peppa un piccolo aiuto fanno un lancio di prova che riesce perfettamente. La bimba, però, nemmeno lo guarda ed è già completamente presa dal suo disegno. Pippo rimane un po’ sgomento, ma le rivolge lo stesso la domanda: “Disegna la traiettoria della ciliegia sia nel mio sistema di riferimento sia in quello di Pappo. La traiettoria deve anche essere rappresentata sia nel piano orizzontale sia in quello verticale”. Il suo sogghigno sparisce velocemente e si trasforma in meraviglia quando, dopo pochi minuti, Peppa presenta i quattro disegni ai due fratelli.
Tutto è perfetto, anche se la traiettoria è eseguita a mano libera e quindi non è molto accurata. Tuttavia, Peppa ha avuto l’accortezza di riportare i valori di distanza e di altezza della ciliegia in alcuni punti fondamentali della traiettoria.
Sapreste imitarla? Ovviamente, non si chiedo nessuna legge del moto e nessun programma predisposto. Non c’è nemmeno bisogno di introdurre masse, forze vere o … apparenti. Una risposta puramente grafica legata ai dati del problema. Dopo, si vedrà…
QUI trovate la soluzione del quiz
QUI trovate tutti gli altri quiz pubblicati nel blog
QUI altri percorsi da calcolare!
17 commenti
Mah... io credo di averlo risolto, ma mi sembra troppo bello per essere vero, quindi mi aspetto il classico trabocchetto zappaliano.
Innanzitutto, per evitare di dover considerare la distanza piedi-mano di Pippo e piedi-bocca di Pappo, ho modificato L rispetto alla figura del quiz.
Considerando solo la forza di gravità e nessun attrito, la ciliegia compie una traiettoria a forma di parabola raggiungendo l'altezza massima a metà percorso.
Quindi questa dovrebbe essere la situazione quando Pappo sta fermo:
Quando Pappo gira con la piattaforma, non cambia niente per Pippo né per la visione orizzontale, ma cambia solo il punto di vista di Pappo che vede la ciliegia solo al momento del lancio (B) e al termine del primo giro (a metà percorso C), per poi ritrovarsela in bocca a termine del secondo giro (A). Quindi vede due punti e non un segmento come quando era fermo...
...o no??
cara Vale... fin qui tutto bene, ma adesso devi disegnare la parte più interessante: la traiettoria della ciliegia nel sistema di Pappo sia in senso orizzontale che verticale... Sicuramente la riceve in bocca, ma come?
Per disegnare la parabola che passa per i due punti con le relative tangenti il metodo grafico più semplice dovrebbe essere quello dell'inviluppo di rette.
Nella seconda parte, aggiungendo il moto rotatorio, la ciliegia si avvicina al bersaglio girandogli intorno....cade dall'alto ma arriva anche "di fianco", al termine di una spirale a passo costante, adagiata sopra una superficie toroidale che nella parte superiore ha il profilo della parabola. Dopo il primo giro l'altezza della ciliegia è massima (vertice della parabola e di fronte al lanciatore) . Alla fine del secondo giro è ridiscesa (all'interno del cratere) alla stessa altezza di partenza, sul bersaglio. Facile da disegnare in 3D. Poi si fanno le proiezioni sui piani richiesti.
A Cuneo questo gioco lo facciamo con i marroni (dopo averli tolti dal riccio)
Giusto per dare l'idea....
Caro Enzo, io ci provo solo due semplici figure, in cui Pappo si ritiene fermo...
La prima mostra la traiettoria della ciliegia (blu) nel sistema di Pappo, vista dall'alto (ho anche mostrato le diverse posizioni della testa pelata di Pippo)...
La seconda mostra la traiettoria della ciliegia (blu quando sale e rossa quando scende), che raggiunge la massima altezza e ricade fino a finire nella bocca di Pappo, vista dal sistema di Pappo...
Paolo
Concordo con i disegni di Paolo, ma c' è un particolare che non mi torna del tutto nel primo disegno.
Se i giri sono esattamente due, la tangente alla spirale nel suo punto finale dovrebbe essere diretta in senso trasversale (sul foglio dovrebbe essere in verticale). Invece sembra orientata per entrare diritta in bocca a Pappo, come se avesse percorso un quarto di giro in più.
Cerco di spiegare meglio il mio dubbio. Nella composizione del movimento entrano in gioco gli spostamenti dovuti al percorso parabolico e alla rotazione. la ciliegia sale e scenda ( questo interessa l'asse verticale) si avvicina al bersaglio ( direzione radiale orizzontale) e ruota attorno ad esso (spirale ).
Al termine della traiettoria ci sono tre componenti: la discesa dovuta alla caduta , l'avvicinamento radiale e la componente tangenziale per la rotazione. Nella proiezione sul piano orizzontale si dovrebbero comporre gli spostamenti radiale e tangenziale per dare la direzione con cui in questo piano il proiettile raggiunge il bersaglio.
Escluderei che questa direzione possa essere la medesima che si avrebbe senza l'effetto del moto rotatorio.
mordi e fuggi (mi attende in ricevimento al ristorante da parenti, non posso mancare....
)
ecco la traiettoria della ciliegia in 3D come vista nel riferimento di Pappo.
A suo tempo le equazioni
Scusa Oreste ho bisogno di capire meglio cosa a tuo avviso non funziona nella prima figura.
Provo a raccontare a voce alta come è stata costruita, così è più facile cogliere eventuali errori.
Innanzitutto ho scomposto la velocità impressa da Pippo alla ciliegia nelle sue due componenti Vx (Vcos α) e Vy (Vsen α).
La componente Vy deve fare i conti con l'accelerazione di gravità, mentre la componente Vx no.
Pertanto rispetto al centro della piattaforma (posizione di Pappo), con lo scorrere del tempo la distanza della ciliegia da Pappo è: d = L – Vx t.
La distanza d è misurata sempre in senso radiale (da Pippo verso Pappo).
Poi c'è la rotazione della piattaforma, per cui a Pappo sembra che tutto intorno a lui ruoti in senso inverso rispetto al suo (ma con la medesima velocità angolare di rotazione).
Nella figura, vista dall'alto, non contano gli spostamenti verticali (dato che manca l'asse y), e sono indicate le posizioni della ciliegia ad intervalli di tempo regolari (0,1 secondi).
Tale posizione tiene conto sia della riduzione nel tempo della distanza della ciliegia da Pappo (posizione in senso radiale; L-Vx t), sia della velocità di rotazione della piattaforma, per cui la ciliegia sembra ruotare in senso inverso di 18 gradi ogni 0,1 secondi (questi sono i valori usati nell'esempio rappresentato dalla figura, ponendo come periodo di rotazione 2 secondi, ossia ω=π/sec=180°/sec).
Mi sembra un po' come il bastone di Archimede che si accorcia, mentre ruota, generando una spirale a passo costante.
In sintesi, nel definire la posizione della ciliegia, mi sembra di aver già tenuto conto anche della rotazione, oltre che della velocità Vx.
Infine, a dir il vero, nel calcolare l'altezza h, io ottengo un risultato diverso da quello di Valentina, ossia ottengo che :
h = 1/4 L Tan (α)
(α) = arctan 4h/L
Magari l'errore è mio
, per cui vorrei chiedere a Valentina come ha ricavato che
h = 1/2 L Tan (α)
Paolo
Caro Paolo, ero certo che il tuo grafico fosse supportato da precisi calcoli, in particolare che ogni puntino blu avesse una sua precisa collocazione. Il fatto è che nella figura mi sembrava che la traiettoria finale fosse allineata con l'asse orizzontale, in linea con la posizione occupata da Pippo, con la conseguenza che la direzione del moto è tutta lungo questo asse. Probabilmente è solo una impressione ottica. La differenza che volevo sottolineare, in questo secondo caso, è la presenza della componente di velocità tangenziale della ciliegia, dovuta alla rotazione di Pappo, assente nel primo caso, di cui hai correttamente tenuto conto.
Per quanto riguarda il calcolo di h che avevo notato anche io nel disegno di Vale, credo che intendesse indicare il punto di incontro delle due tangenti nei punti iniziale e finale, che peraltro non compare nel suo grafico, piuttosto che la posizione del vertice della parabola.
In effetti alla base delle due figure c'è un ragionamento logico e matematico.
Come dicevo nel precedente messaggio l'altezza della ciliegia dipende sia dalla componente Vy sia dell'accelerazione di gravità, ossia:
h = Vy t1- ½ g t1²
dove t1 è il tempo impiegato per raggiungere la massima altezza.
La ciliegia, però, sale e poi riscende, per cui h (che varia nel tempo) alla fine deve diventare di nuovo uguale a zero h0:
h0 = 0= Vy t- ½ g t²
Vy t = ½ g t²
2Vy/g= t²/t
t = 2Vy/g
Il tempo t è esattamente il doppio di t1 (tanto ci mette la ciliegia per salire fino all'altezza massima, tanto ci mette per tornare alla stessa altezza iniziale), per cui:
t = 2 t1
t1 = ½ t = ½ 2Vy/g
t1 = Vy/g
Sostituendo t1 nell'equazione per ricavare l'altezza massima h, si ha:
h = Vy (Vy/g) - ½ g (Vy/g)²
h = Vy ²/g - ½ g Vy²/g²
h = Vy²/g - ½ Vy²/g
h = ½ Vy²/g
che si può scrivere come:
h = ½ Vy Vy/g
ma Vy/g = t1
h = ½ Vy t1
da cui ricavo nuovamente t1:
t1 = 2 h/Vy....o volendo ricavo: Vy = 2h/t1
ma nel medesimo tempo la ciliegia ha percorso ½ della distanza L tra Pippo e Pappo:
t1 = L/2Vx... o volendo ricavo: Vx = L/2t1
eguagliando:
2 h/Vy =L/2Vx
h = 1/4 L Vy/Vx
ma Vy/Vx = V sen (α) /Vcos (α) = Tan (α)
h = 1/4 L Tan (α)
4h/L = Tan (α)
(α) = arctan 4h/L
Nel medesimo tempo t1 Pappo compie un giro completo, per cui la velocità angolare espressa in radianti è pari a: ω = 2π/t1
sostituendo t1 =Vy/g
ω = 2π/(Vy/g)
ω = 2πg/ Vy
oppure sostituendo t1 = 2 h/ Vy
ω = 2π/(2h/Vy) = π Vy/h
ω = π Vy/h
o anche sostituendo t1 = L/2Vx
ω = 2π/(L/2Vx) = 4 π Vx/L
ω = 4 π Vx/L
Per trovare il valore del modulo di V, si possono usare diversi metodi, tra cui:
Vy = V sen(α)
V = Vy/sen(α)
oppure:
Vx = V cos(α)
V = Vx/cos(α)
e ancora
h = ½ Vy²/g
Vy² = 2hg
Vy = √2hg
V =(√2hg)/sen(α)
A me sembra filare, però non si sa mai..
Paolo
sono di ritorno dal ricevimento al ristorante. Oddio, dite che ho alzato un po' il gomito ?....
mamma mia, mamma mia... volevo solo un grafico semplice semplice ... è inutile i maghi sono proprio incapaci di non fare magie...
Aggiungerei solo questa osservazione: in ogni istante esistono 3 componenti della velocità. quella che chiami Vy , orientata come l'asse verticale (salita e caduta), quella diretta verso il punto centrale in cui si trova Pappo, (che hai chiamato Vx) ed una velocità tangenziale (perpendicolare al raggio) che chiamerei Vt=ωd =ω(L – Vx t ).
Nella proiezione (vista dall'alto) sul piano orizzontale le componenti Vx e Vt dovrebbero sommarsi vettorialmente per dare la velocità risultante su quel piano.
Dato che la Vt è proporzionale alla distanza dal centro (punto di arrivo finale), che va riducendosi al passare del tempo t, il suo valore diminuisce progressivamente, fino ad azzerarsi quando viene raggiunto l'obiettivo (distanza d = 0). Prima di quell'istante il suo valore non è nullo e determina modulo e orientamento del vettore velocità sul piano.
Maurizio
Ma Peppa non conosce molto di matematica e fisica... stiamo bassi vi prego
Hai ragione tra la (splendida) animazione da mal di mare di Arturo e le elucubrazioni mentali mie e di Maurizio, povera Peppa!
Peppa, tappati per un attimo le orecchie...
Maurizio ho capito cosa intendi, però al posto della velocità tangenziale (e della sommatoria vettoriale che richiede), a mio avviso si può usare direttamente la velocità angolare, che indica come cambia l'angolo di posizione della ciliegia nel tempo e la relazione d= L- Vxt per determinare la distanza radiale dal centro piattaforma...
Arturo, sulla tua animazione ho un dubbio... se guardo la figura 2, la piattaforma ruota in senso antiorario, per cui per Pappo la ciliegia dovrebbe ruotare in senso orario... mi sembra che nell'animazione non sia così.. sbaglio?
Paolo
Paolo, si, l'animazione è solo un giro panoramico intorno alla traiettoria tridimensionale percorsa dalla ciliegia da Pippo verso Pappo. Il verso di rotazione dell'animazione non è in relazione con quello fisico di Pappo. Ho ricostruito la traiettoria tridimensionale col solito geogebra, partendo dalle leggi del moto del caso in esame e risalendo alle tre equazioni parametriche della curva x(
)=... , y(
)=... , z(
)=... dove 
è l'angolo di rotazione di Pappo (o della ciliegia..). Una volta ottenuta la traiettoria, ho fatto partire l'animazione di default del programma , che percorre appunto un giro panoramico attorno all'oggetto geometrico, senza preoccuparmi del verso di rotazione.