Quiz: un ricetrasmettitore un po' debole.
Per sfuggire al gran caldo della città Oreste si è trasferito per una breve vacanza, a Mels, un piccolo paese della Svizzera, nel Canton San Gallo, dove le temperature sono una decina di gradi più basse.
La scelta della località non è stata casuale, perché proprio in quel paese abita il cugino Geremia, grande appassionato di matematica, geometria ed elettronica.
Geremia è felicissimo dell'arrivo inatteso di Oreste, anche perché, rovistando in soffitta, ha trovato un vecchio kit di costruzioni elettroniche degli anni '70 che, tra vari esperimenti, propone anche la costruzione di un ricetrasmettitore a onde corte. Realizzare questa apparecchiatura con la collaborazione del cugino sarà certamente per ambedue una divertente esperienza.
In un' epoca di smartphone, è curioso che si senta il bisogno di un oggetto così rudimentale, ma il fascino del vintage ha la sua presa. E poi, costruire con le proprie mani e collaudare un ricetrasmettitore è sempre una bella soddisfazione.
Oreste e Geremia, seguendo diligentemente le istruzioni, completano la costruzione in brevissimo tempo. Ora si tratta di vedere se tutto funziona, se il segnale trasmesso viene adeguatamente ricevuto. Ma fino a che distanza sarà possibile mantenere la comunicazione? Secondo Geremia la cosa più semplice per scoprirlo, sarebbe allontanarsi durante la conversazione finché il segnale si indebolisce al punto di non essere più intellegibile.
Ma a Oreste le cose semplici non piacciono, e sapere quale sia la portata del segnale trasmesso non gli sembra così importante. Quindi propone a Geremia il seguente "esperimento mentale" che vi giriamo come quiz della settimana.
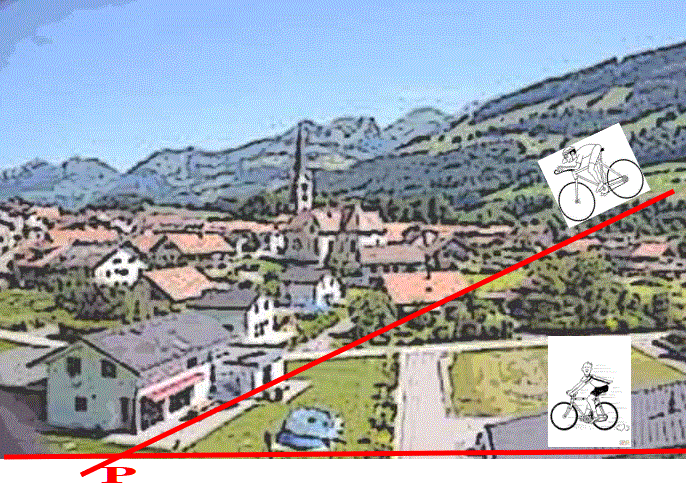
Dice, Oreste: "Supponiamo che tu ed io ci si trovi su due rette perpendicolari, che si incontrano in un punto P. Queste due rette sono strade pianeggianti e rettilinee e noi siamo rispettivamente a 150 Km e 210 Km dal punto di intersezione. Immaginiamo di partire, a mezzogiorno in punto, muovendoci dalla nostra posizione iniziale, verso P, in bici , alla velocità costante di 30 Km/ora, mentre ci scambiamo messaggi con il ricetrasmettitore. Naturalmente all'inizio non saremo in grado di comunicare, ma ad un certo punto la distanza si sarà ridotta abbastanza per poter parlare in modo abbastanza intellegibile. Ci sarà poi un momento in cui la distanza tra di noi sarà minima e il segnale ricevuto sarà alla sua massima intensità. Ecco, sarebbe bello sapere a quale ora questo si verificherà e quale sarà la distanza che ci separa in quell'istante preciso.
Geremia, dopo una rapido calcolo, è in grado di fornire la risposta esatta ai due quesiti di Oreste.
Siamo fiduciosi che i nostri lettori sapranno fare altrettanto.
QUI la soluzione
15 commenti
Domanda: quando uno dei due arriva nel punto d'incrocio deve proseguire o fermarsi? Direi proseguire... OK?
si, prosegue
Dopo 6h.
Si trovano entrambi a 30km da P. Uno dei due lo ha oltrepassato l'altro ci deve ancora arrivare. Tra i due la distanza è circa 42 km (30×\/2).
Trascuro la velocità finita del segnale.
Mik,ovviamente per adesso non possiamo dire niente..aspettitamo anche le altre risposte
Io, a quell'ora, prendo sempre l'aperitivo... in qualsiasi punto del perimetro della casa. Abitudini cuneesi... vero Oreste?
Confermo. Pare addirittura che i vicini di casa abbiano preso l'abitudine di regolare gli orologi sul primo sorso....
Conoscendo la tendenza "analitica" di alcuni maghi... vi propongo un aiutino puramente geometrico...
Propongo un approccio puramente geometrico che sfrutti una caratteristica delle diagonali dei rettangoli aventi uguali perimetro.
Ovviamente, di tutto il percorso c’interessa solo quello che inizia con l’arrivo del ciclista A nel punto d’incrocio. Ammettiamo che sia quello che viaggia in orizzontale. In quell’istante il suo collega B deve essere a una distanza (lungo la direzione verticale) pari a 60 km (viaggiano alla stessa velocità, con una differenza di 60 km).
Facciamo procedere B verso il punto d’incrocio di una lunghezza h qualsiasi. Data la velocità uguale, nello stesso intervallo di tempo A si è spostato dello stesso valore h verso destra. Otteniamo il rettangolo B’PA’Q Che ha come lati h, 60 –h, h e 60 – h. La sua diagonale PQ non è altro che la distanza tra i due ciclisti A’ e B’. Continuando a togliere e aggiungere h ai due ciclisti, cambia il rettangolo, ma il perimetro resta uguale. E così via fino a che B arriva in P e A in A”.
Una proprietà dei rettangoli di uguale perimetro è quella che dice che la minima diagonale si ottiene per il quadrato, ossia per una configurazione come quella disegnata in rosso. Ne segue che la minima distanza si ha a metà strada tra B e B’’ e A e A”.
Che questa sia la minima distanza si vede subito unendo gli spigoli esterni dei rettangoli: essi stanno ovviamente su una retta (per costruzione) e la minima distanza tra P e questa retta deve essere la perpendicolare, ossia PM.
Ne segue che la minima distanza si ha per 30(2)1/2.
L’ora di tale configurazione sono le 18. Infatti, A arriva in P 5 ore dopo la partenza (150/30), ossia alle 17, ma poi deve ancora percorrere la metà di 60 km, ossia 30 km che corrispondono a un’ora.
come si dice in questi casi..la classe non é acqua.Finalmente anche tu hai partecipato ad un nostro quiz, che ha avuto dei risvolti geometrici inaspettati.Grazie per aver partecipato. Adesso ci aspettiamo lo stesso una dimostrazione analitica
Coraggio, manca una dimostrazione analitica; piccolo suggerimento:
è possibile esprimere la distanza fra le due biciclette in funzione del tempo t? Ovvero trovare una funzione del tempo d(t)? Dopodichè...
qualcuno riesce ad impostare la funzione?
Posizioniamo i due ciclisti, diciamo X e Y, lungo gli assi di un piano cartesiano dove (inizialmente) si muovono ortogonalmente verso l'origine
, che facciamo coincidere col punto P, con la medesima velocità 
. Li posizioniamo lungo gli assi del piano cartesiano. L'equazione del moto dei due è:
X: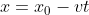
Y: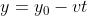
dove:
In ogni momento la distanza tra i due è:
La ricezione è massima laddove la distanza è minima. Per trovare il minimo della distanza si eguaglia a zero la derivata nel tempo, ma mi permetto una semplificazione e affermo che)
è minima laddove anche ^2)
è minima, e quindi posso fare meno fatica schivando le radici e trattando il quadrato della distanza:
Derivando ambo i lati rispetto al tempo:
Eguagliando a zero e svolgendo i calcoli:
il che ci dà l'istante al quale si ha la distanza minima. Sostituendo i valori si ottiene:
Dopo 6 ore i due ciclisti si trovano rispettivamente in:
X: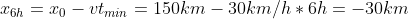
Y: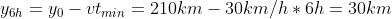
ovvero si trovano ai vertici opposti di un quadrato di lato 30km (cfr. disegno di Vincenzo più sopra) e pertanto distano ovviamente:
finalmente! Adesso ci resta la curiosità di come tu avessi trovato la soluzione già prima, praticamente senza alcun calcolo
No no avevo fatto i calcoli ma non avevo un PC per scrivere il tutto in modo ordinato... e poi magari qualcun altro voleva dire la sua...
capisco