Questo lungo articolo è stato inserito nell'approfondimento dedicato alla velocità della luce che tratta l'argomento in modo organico

 

Chi più chi meno, tutti conosciamo gli effetti principali della relatività ristretta. Abbiamo perfino scritto una favola sul muone… Da non molto abbiamo anche completato una lunga trattazione, a tutti i livelli, sull’aberrazione luminosa. Non dovremmo quindi avere problemi a risolvere dei piccoli problemi che sorgono quando si ha a che fare con un oggetto che si muove a velocità prossime a quella della luce e con una macchina fotografica che vuole riprendere la scena.

Stiamo attenti, però, a discriminare bene ciò che si misura e ciò che si vede o -meglio- che viene catturato dalla macchina fotografica. Sappiamo bene che la velocità della luce è piuttosto lenta e la sua limitazione si pone bene in risalto quando quello che vogliamofotografare si muove a velocità comparabile, Ne vedremo (è proprio il caso di dire così...) delle belle!

Andiamo avanti a quesiti, in modo da rendere più vivace la trattazione. Cominciamo con il caso più semplice:  fotografiamo un righello!

Un righello relativistico

La situazione è quella che viene mostrata in Fig. 1. La macchina fotografica si trova in F, mentre il righello ha una lunghezza L quando è fermo.

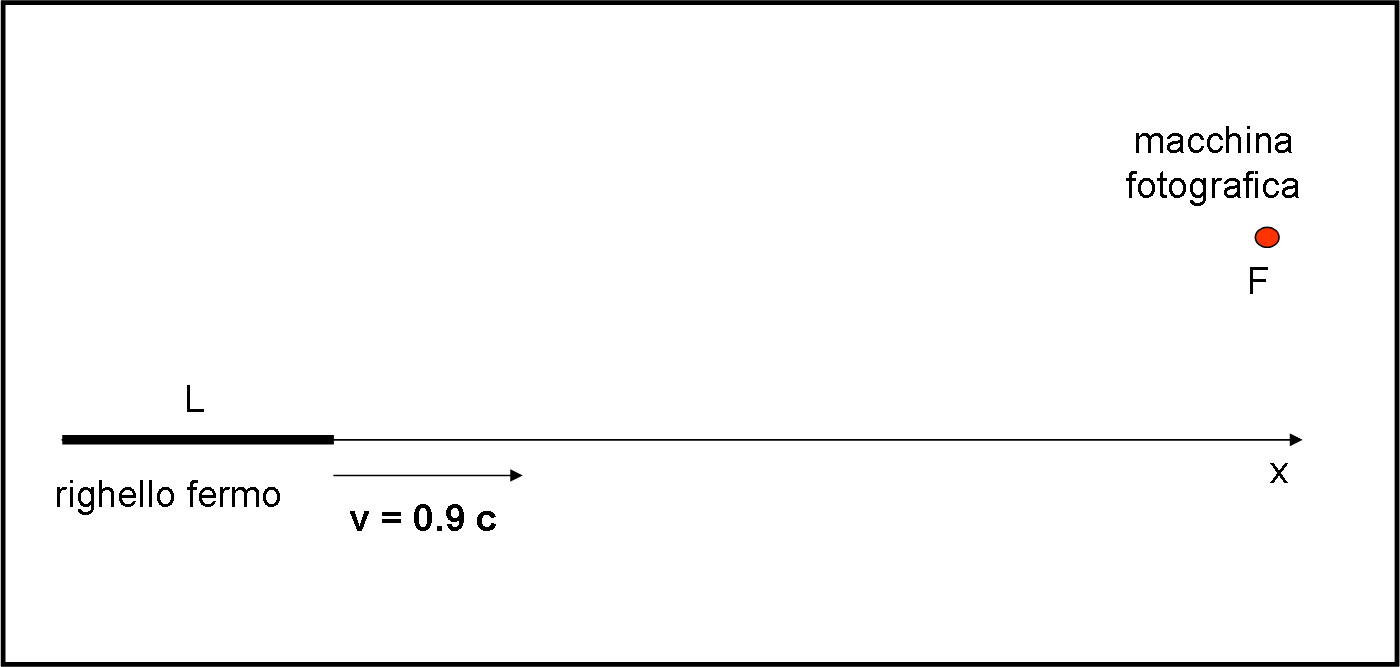
Il righello viene messo in moto con velocità v = 0.9 c  (c = velocità della luce) lungo l’asse x. A un certo istante t_o la macchina fotografica scatta una foto al righello. La domanda è semplice…: “Come sarà visto il righello nell’immagine catturata dalla macchina fotografica? Più corto di quando era fermo, più lungo o perfettamente uguale?”

A questo quesito si può rispondere senza usare formule. Anche chi sa ben poco della RR può dare la risposta… basta un po’ d’intuito e di ragionamento.

Abbiamo usato la macchina fotografica perché ci garantisce che ciò che viene immortalato nell’immagine è ciò che capita esattamente in un certo istante t_o.

Si può facilmente pensare anche a cosa capiterebbe se il righello andasse in verso opposto, ossia con velocità - 0.9 c.

Stiamo attenti, perché la relatività ristretta sembrerebbe vacillare...

Per rispondere alla domanda  bisogna fare una premessa: la richiesta si riferisce a quello che rimane impresso sulla pellicola della macchina fotografica (MF) e non su quello che potrebbe essere misurato in un sistema in quiete. Siamo di fronte a un oggetto di dimensioni finite che si muove ad alta velocità lungo una direzione qualsiasi rispetto a una macchina fotografica, che è considerata in un sistema fermo.

Misurando la lunghezza del righello nel sistema della MF siamo obbligati a ritrovare la contrazione delle lunghezze dovuta alla Relatività Ristretta (RR). Tuttavia, quello che ci interessa è: “Si fotografa o non si fotografa la contrazione di Lorentz? E se non si fotografa, cosa appare sulla pellicola?” Siamo, perciò, di fronte a un’apparenza e non a una realtà fisica vera e propria. Tuttavia, anche l’aberrazione luminosa è un’apparenza e non possiamo certo trascurarla. Inoltre, ciò che appare alla fine è dovuto a un fenomeno fisico (la limitatezza della velocità della luce) e quindi l'apparenza ha tutto il diritto di essere considerata un fenomeno fisico in piena regola.

Immaginate un tentativo fatto per misurare la lunghezza di una certa particella superveloce. La cosa migliore sarebbe riuscire a fotografarla… ma allora devo sapere esattamente come tornare indietro dalla foto alle dimensioni “reali” sia contratte dalla RR sia in quiete (quest’ultimo passaggio ce lo regala Einstein con la RR). A prima vista sembrerebbe un problema non facile, ma, in realtà, almeno da un punto di vista qualitativo, gli ostacoli sono irrisori. Il livello scelto da noi è mantenuto molto basso, ma sufficiente a spiegare apparenze apparentemente assurde ma del tutto spiegabili con un minimo di ragionamento.

Come aiuto preliminare si potrebbe fare un esempio terra-terra, conosciuto da tutti, ma che può essere illuminante e decisivo per la soluzione più immediata.

Il tutto, in fondo, si collega a ciò che fotografiamo puntando una MF verso il cielo. L’importante è considerare un “clic” istantaneo, capace di raccogliere la luce che arriva in un certo istante perfettamente definito senza tener conto di integrazioni luminose successive. Questa è la causa principale dell’utilizzo della MF e non dell’occhio che continua a immagazzinare luce…

In una istantanea del cielo notturno (Fig. 2)  possiamo tranquillamente vedere galassie, stelle, pianeti e magari anche qualcosa di più vicino (se è illuminato). Cosa possiamo dire a riguardo? Una cosa semplicissima che è ormai patrimonio di tutti: “La luce che giunge alla MF proviene dall’Universo, ma è partita in tempi decisamente diversi!” (come questi scolari che, partiti dalle loro case in orari diversi, arrivano a scuola e vengono visti dal custode contemporaneamente).

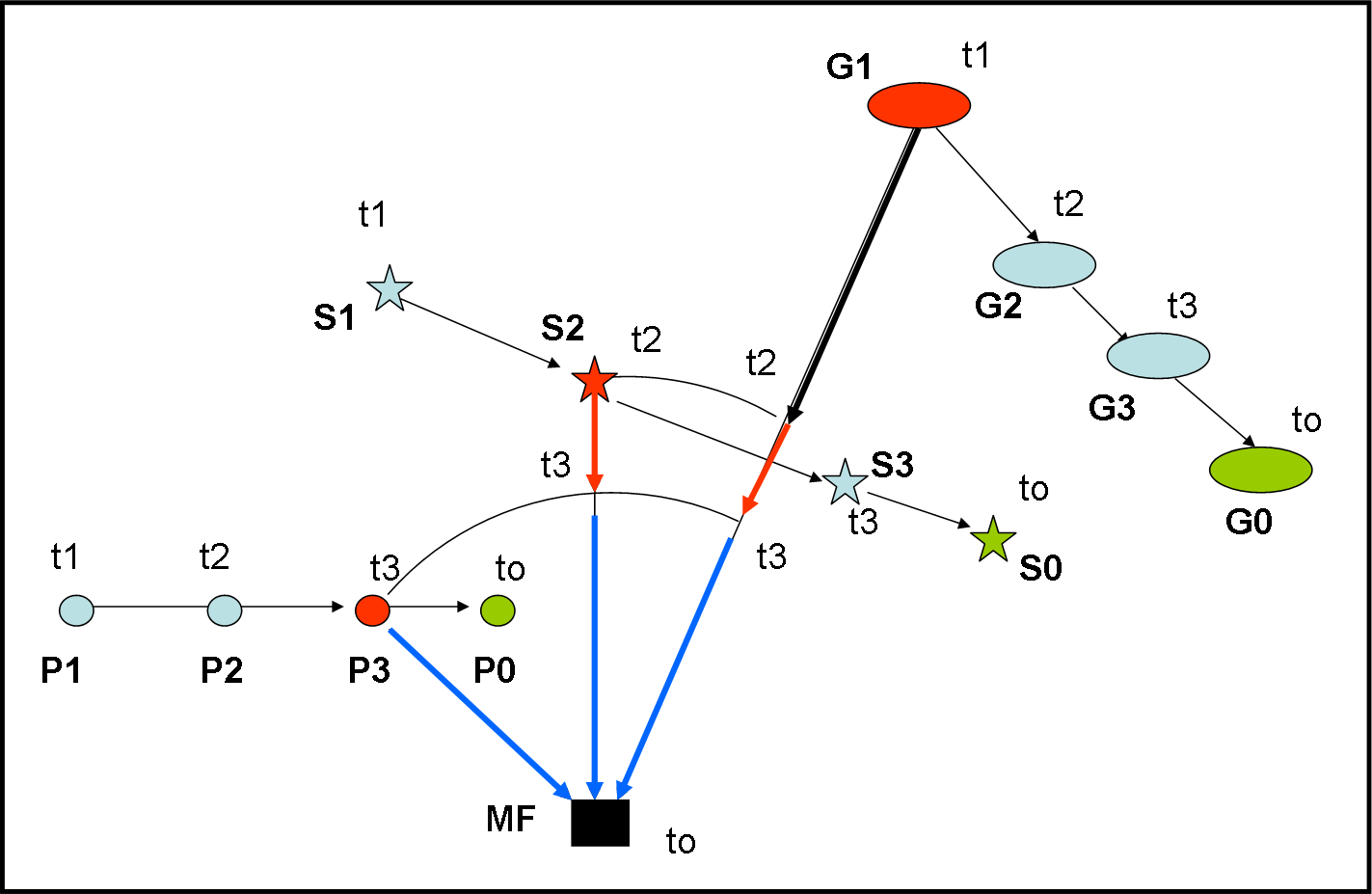
Quella relativa alla galassia è partita milioni o miliardi di anni fa, quella della stella qualche decina o centinaia di anni fa, quella del pianeta ore o minuti fa, quella della casa illuminata solo frazioni di secondo fa. Eppure questo è quello che vediamo sulla pellicola. (Vi ricordate la linea ferroviaria  all’inizio del corso di matematica? Ebbene se la fotografo dovrei dedurre che due rette parallele si incontrano sicuramente! Chiamiamola pure prospettiva, ma è comunque ciò che si vedrebbe sulla pellicola. L’aggancio con geni come Masaccio & co. ci fa capire come l’arte sia sempre stata in stretto contatto con la fisica, ma non solo. Da qui il nostro bisogno di allargare sempre i vari discorsi e ragionamenti. Il nostro paracadute deve sempre aprirsi al tempo giusto!).

Una realtà solo visiva, un’apparenza, dato che nel momento dello scatto fotografico, la galassia, la stella e il pianeta si sono già spostati dalle posizioni di partenza della loro luce. Tuttavia, lo scatto fotografico, sapendo con cosa abbiamo a che fare, diventa la realtà fisica  su cui possiamo svolgere le nostre analisi scientifiche. Rimane il fatto fondamentale che la posizione di ogni oggetto ripreso è relativa a un tempo di partenza diverso e quindi abbiamo di fronte una rappresentazione legata soprattutto alla lentezza della luce.

Non guardate con attenzione i moti degli oggetti celesti, li ho disegnati a casaccio, senza alcuna legge di meccanica celeste. L’importante è capire il concetto di base.

La galassia è l’oggetto più distante e, affinché la sua luce arrivi sulla MF al tempo to, deve partire al tempo t1. E’ facile vedere la posizione dei tre oggetti al tempo t1. Tuttavia, la luce, che S e P devono inviare affinché arrivi su MF al tempo to, DEVE ASPETTARE, in quanto se partisse al tempo t1 arriverebbe alla MF molto PRIMA di quella della galassia (loro sono molto più vicine).

La prima che passa all’azione è la stella quando è nella posizione S2. In quelle condizioni, infatti, la distanza che deve percorrere la luce da S2 a MF è esattamente uguale a quella che deve ancora percorrere la luce partita da G1 in t1, per arrivare in MF. E’ facile determinare questo istante… basta tracciare una circonferenza di centro MF che passi da S2 e vada a incontrare il tragitto del fotone di G1. Il fotone della stella può accodarsi a quello galattico. Disegniamo in rosso il tragitto “concorde” del fotone galattico e di quello stellare.

Il pianeta P sta ancora aspettando, dato che è più vicino e la luce inviata fino ad ora arriverebbe su MF molto prima del tempo to. Il momento per far partire il fotone planetario che ci interessa è t3, dato che in quell’istante la distanza che deve percorrere è esattamente uguale a quella del fotone stellare e di quello galattico. Anche l’ultimo fotone si allinea con gli altri due e insieme percorrono il tragitto blu che li fa arrivare CONTEMPORANEAMENTE su MF al tempo to.

Cosa vediamo sulla pellicola? La galassia in G1, la stella in S2 e il pianeta in P3. Una configurazione (oggetti rossi) che non ha nessuna corrispondenza con la realtà dei fatti… Al tempo t1 la vera configurazione sarebbe stata data da P1, S1 e G1. Al tempo to la vera configurazione sarebbe Po, So e Go (oggetti verdi). E analogamente per i tempi t2 e t3.

In poche parole (e senza nessuna formula), tenendo solo conto del fatto che la luce è piuttosto “lenta” (chissà cosa vedremmo se fosse diversa...), l’immagine che otteniamo è un mix caotico di spazio e tempo, che ben poco ha a che vedere con configurazioni reali degli oggetti singoli. Tuttavia, è tutto ciò che possiamo ricevere da questo tipo di informazione e ci dobbiamo accontentare… La scienza, però, è riuscita a districarsi e a capire come sono andate le cose, facendo più fotografie e confrontando i risultati.

Questa trattazione è giocoforza banalizzata e semplificata, dato che non tiene conto dell’espansione dell’Universo e dei veri moti degli oggetti celesti e della stessa MF. Tuttavia, è più che sufficiente a capire cosa vediamo sulla pellicola quando facciamo muovere velocemente il nostro righello.

Nell’esempio precedente abbiamo utilizzato oggetti diversi… nel caso del righello l’oggetto è unico, ma si muove in modo rapidissimo: le conclusioni sono estremamente simili…

Questa trattazione quasi "ridicola" può essere molto utile quando cominceremo a complicare un po' le cose...

 

Premessa (per i meno esperti)

I fotoni sono le particelle-non particelle che trasportano la luce e riescono a esistere solo viaggiando alla massima velocità possibile, quella della luce, appunto. In realtà, se non corressero, non avrebbero massa e sparirebbero nel nulla: chi ha visto un fotone fermo alzi la mano! Senza di loro non si vedrebbe niente…e tutto sarebbe buio e triste.

I fotoni sono le “particelle” più allegre dell’Universo, essendo libere di muoversi e di scontrarsi con i loro grandi amici elettroni, che a volte li seguono nel loro girovagare continuo, altre volte no, ma il divertimento è sempre assicurato. Chi non ci crede vada a leggere la QED e/o la fisica papalliana…

Tra di loro non esiste invidia o gelosia, dato che sono tutti uguali, malgrado possano cambiare colore ed energia a seconda del balletto che compiono mentre viaggiano. Sappiamo già che, a volte, questo cambio di colore è del tutto apparente, ma il risultato è sempre estremamente fantasioso e apprezzato da tutti i corpi celesti. Fare apparire le cose come non sono in realtà… ecco un gioco che a loro piace moltissimo e di cui anche gli uomini sono consapevoli (aberrazione, effetto doppler, miraggi, fate morgane e mille altre diavolerie del genere). In particolare, si divertono a prendere in giro quel sapientone di Albertino (il mago che avete conosciuto QUI). Gli vogliono un gran bene, tanto che gli hanno regalato perfino un Premio Nobel (effetto fotoelettrico), ma fanno di tutto per metterlo in agitazione e in difficoltà, combinandogli scherzi insospettabili. Poi tutto finisce con una bella risata…

Albertino si vanta tanto (e giustamente) della sua Relatività Ristretta e non perde occasione per farsi bello e dimostrare che può spiegare praticamente tutto (compresa la strana massa dei fotoni, che proprio massa non è). E allora è proprio su questa teoria inattaccabile che scatenano la loro fantasia.

A volte, però, la cosa capita quasi senza volerlo.

Si tramanda una storia molto simpatica che vede come attori principali due amici per la pelle, il fotone A e il fotone B, destinati a vivere separati ai due estremi di un righello di lunghezza d₀. In realtà, loro non vivono da fermi, ma possono facilmente essere creati in un certo posto e a un certo tempo. Il discorso non è facile da spiegare, ma a noi interessa poco in questa avventura, ormai diventata celebre nel mondo fotonico. Immaginiamo, quindi, che A e B esistano potenzialmente nei due estremi del righello, pronti a nascere e spiccare il volo. Ovviamente, sul righello vi sono moltissimi altri fotoni potenziali (anche nella stessa posizione di A e di B), pronti a partire continuamente. In altre parole, dato che i fotoni trasportano la luce, il righello è sempre illuminato. Ma noi interessa soltanto (per adesso) la storia dei due amici per la pelle.

Una favola molto reale

Tutto nasce proprio da Albertino che, ancora una volta, vuole dimostrare quanto bella e perfetta sia la sua teoria. Lui ha preso un righello (proprio il loro righello) e ha deciso di farlo muovere a grande velocità, poco meno di quella a cui viaggiano normalmente i fotoni. Come previsto il righello si accorcia (e i potenziali fotoni A e B si avvicinano) e tutte le misure eseguite da chi sta fermo rispetto al righello non possono che confermarlo. Ancora una volta Albertino ha stupito il mondo! La nuova lunghezza d è minore di d₀. Questo momento di stupore e ammirazione è rappresentato in Fig. 1.

“Come sarebbe bello farci fotografare mentre viaggiamo a questa velocità” pensano i due fotoni. Bastava che venissero eccitati, sarebbero nati e si sarebbero lanciati verso la macchina fotografica M e sarebbero apparsi entrambi nella fotografia. Una bella foto, con i due fotoni agli estremi e il righello accorciato che li unisce, segnalato da tutti gli altri amici dislocati lungo l’asta.  Sarebbero stati molto più vicini!

A e B erano già stati fotografati, ma con il righello fermo, ossia con una distanza tra di loro uguale a d₀. Loro sapevano bene come fare… partiva il fotone A, mentre il fotone B aspettava che A arrivasse a una distanza dalla macchina fotografica M uguale alla sua; poi partiva anche B che sarebbe giunto insieme all’amico nello stesso istante t₀, quello del “clic” della macchina fotografica (viaggiando alla stessa velocità e avendo lo stesso spazio da percorrere, sarebbe stato uguale anche il tempo impiegato). Un lavoro di “routine” che conoscevano molto bene.

L’importante era che A partisse a un certo tempo t_A e che B partisse un po’ dopo, al tempo t_B. Ripetiamo: se B partisse insieme ad A, arriverebbe su M molto prima dell’amico, dato che la distanza BM è più corta di AM e loro viaggiano alla stessa velocità (come già detto, non possono rallentare). B doveva, perciò, aspettare che la distanza tra l’amico A e M diminuisse fino a diventare uguale alla sua.

Ovviamente non erano solo loro a fare quel gioco. In ogni istante, dal righello partivano dei fotoni diretti verso M, ma, ovviamente, alcuni arrivavano in M prima, altri dopo, del tempo t₀. Solo quelli che si accodavano al viaggio di A, partendo quando la distanza tra loro ed M era uguale a quella di A da M avrebbero raggiunto insieme ad A e B la macchina fotografica nel momento t₀ dello scatto. La Fig. 2 ci mostra una serie di fotoni del righello che sono partiti ai tempi giusti (compresi tra t_A e t_B), in modo da essere, al tempo t_B, tutti alla stessa distanza da M. Questi fotoni, compresi tra A e  B, sono gli unici che saranno visibili nell’immagine ripresa da M all’istante t₀. Ovviamente la distanza tra A e B rimane sempre la stessa, ossia d₀.

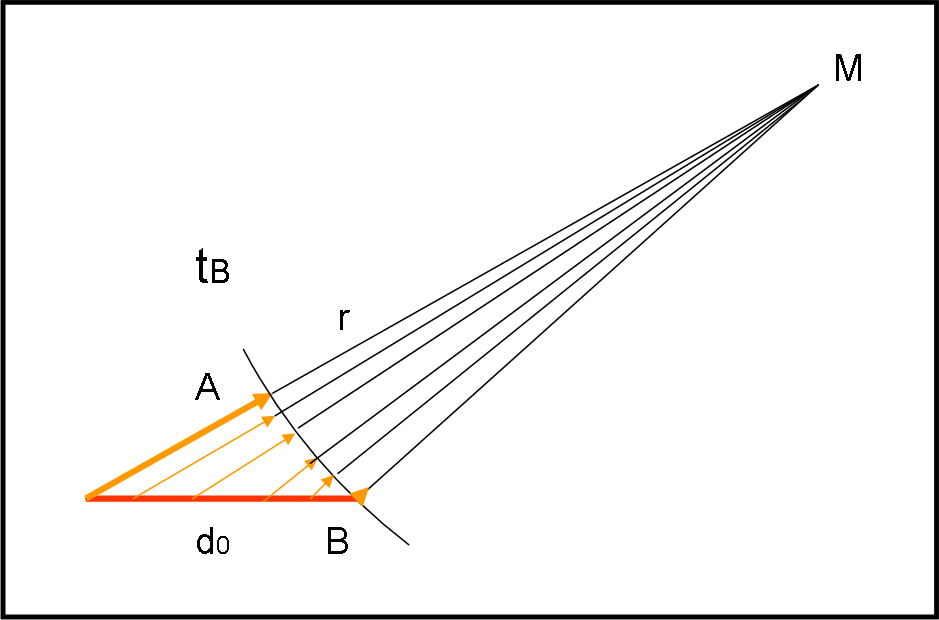
A e B sono così amici che il solo pensiero di avvicinarsi li emoziona. Il righello sta viaggiando a una certa velocità v e il fotone A si fa coraggio e decide che è il momento di partire verso la macchina fotografica M: sarebbe arrivato da lei proprio nel momento t₀ stabilito per lo scatto istantaneo (la foto avrebbe ripreso solo ciò che sarebbe arrivato da lei in quel momento esatto: chi c’è c’è e chi non c’è non c’è!).

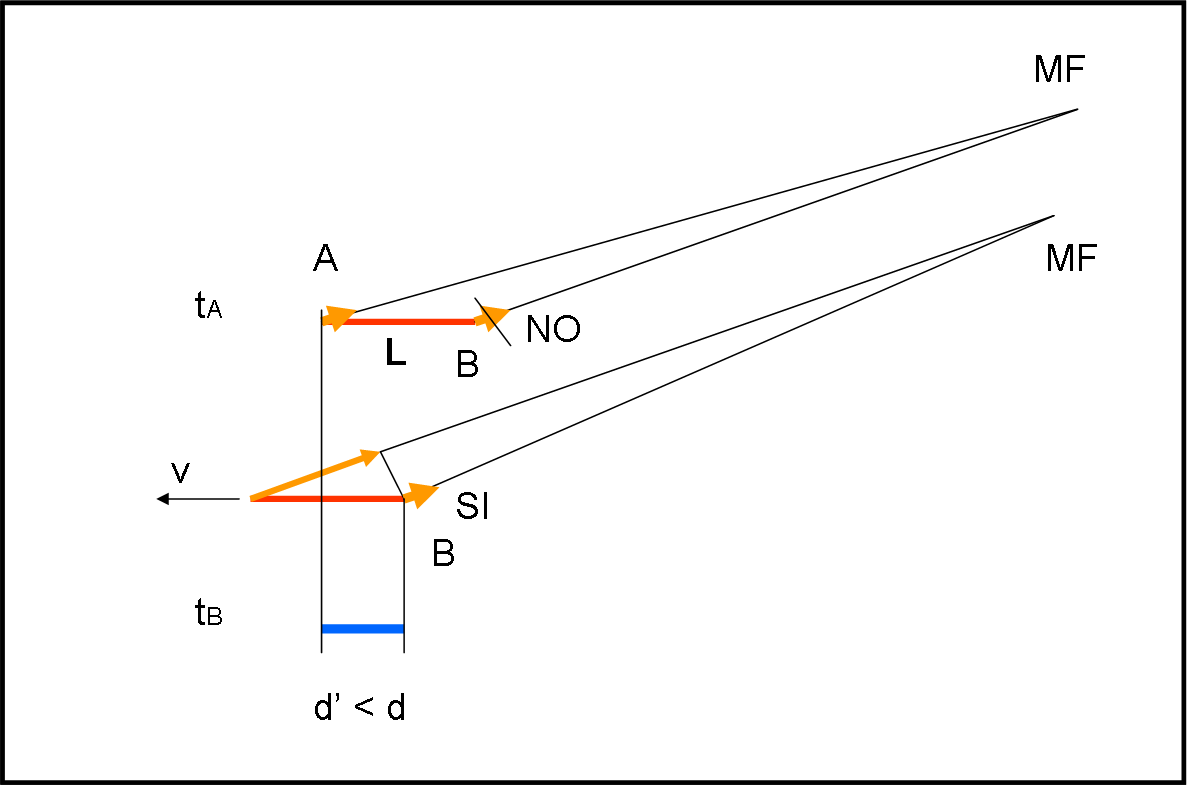
Il fotone B scalpita per partire anche lui, ma sa che non può farlo subito, come già detto precedentemente e come mostra il primo riquadro della Fig. 3, a partire dall’alto.

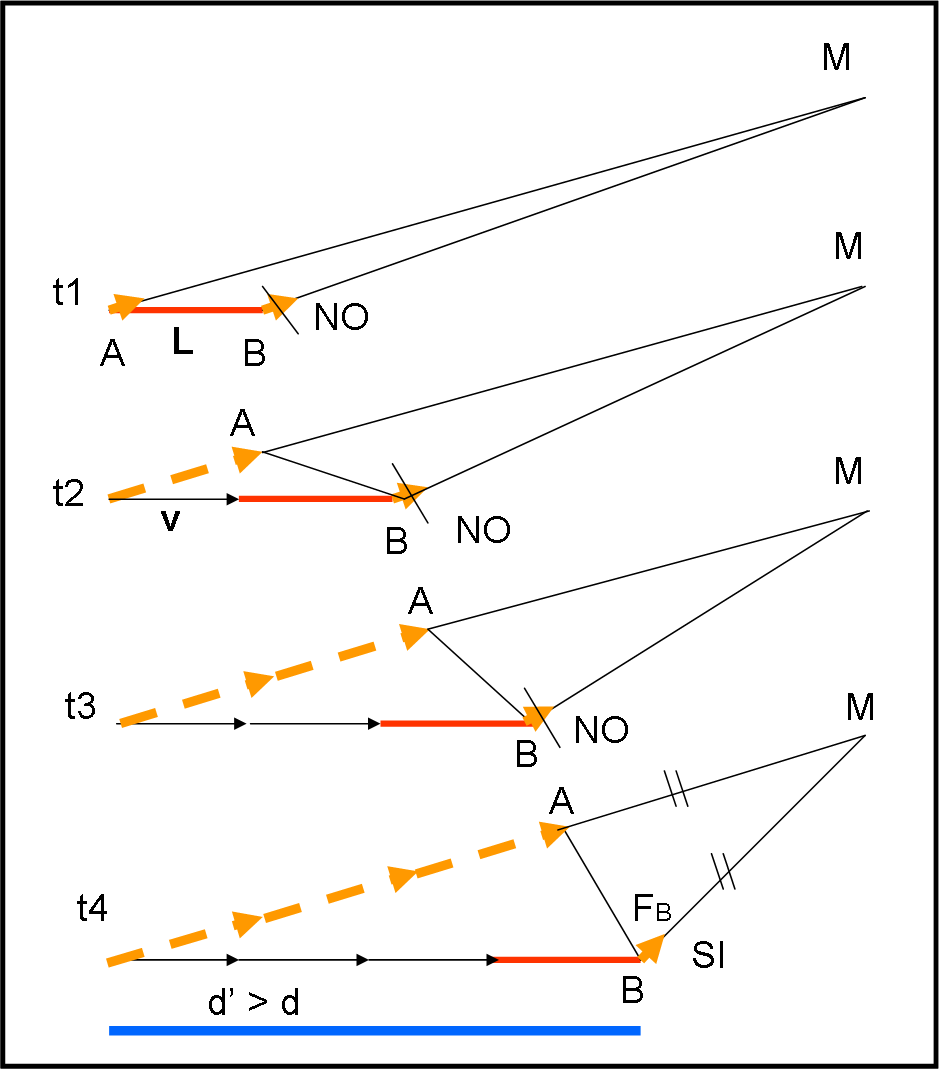
Lascia passare un secondo (di solito bastava…) e rifà la sua misura: accidenti, è sempre più avanti di A. La spiegazione è facile: mentre A ha percorso la freccia gialla tratteggiata, lui si è mosso verso destra con una velocità v, non molto più piccola di quella della luce, ossia la loro. B deve ancora aspettare (secondo riquadro dall’alto della Fig. 3). Potesse farlo, B sarebbe tutto sudato…

Passa un altro secondo e la situazione è quella del terzo riquadro della Fig. 3. B comincia a rincuorarsi. Si è accorto, infatti, che la differenza tra il percorso che deve fare lui per arrivare a M diventa sempre più simile a quello che manca ad A per arrivare alla macchina fotografica nello stesso istante t₀. Comincia ad eccitarsi e si prepara al volo. Ormai è questione di poco…

Un altro secondo è trascorso (ma poteva anche essere di meno…) e la configurazione diventa quella dell’ultimo riquadro in basso. Non c’è più dubbio: la distanza tra A, già in viaggio da un po’, ed M è ormai perfettamente uguale alla distanza tra B ed M. E’ il momento di partire, dato che uguale distanza e uguale velocità vogliono anche dire tempo uguale. A e B arriveranno sicuramente su M nello stesso istante t₀, come se si dessero la mano. E così avviene!

Perfetto, A e B sono sicuri di essere stati immortalati nella foto e sono anche sicuri che appariranno più vicini di quando il righello era fermo, dato che Albertino ha dimostrato attraverso misure precise che la lunghezza si è accorciata.

Pochi attimi e possono guardare la foto… Accidenti, questa non se la aspettavano (e nemmeno Albertino che diventa bianco in volto). La distanza tra A e B (che si vedono benissimo nella foto, essendo agli estremi del righello) è molto più grande di quella prevista (e misurata) da Albertino, ma anche di quella che era all’inizio, prima di essere accorciata.

Un attimo di ragionamento e tutto appare chiaro: la posizione di A, sulla pellicola fotografica, si riferisce all’istante t₁ in cui è partito. La posizione di B si riferisce, invece, all’istante in cui B ha lasciato il righello, ossia quella relativa al tempo t₄. In poche parole, ciò che si vede nella fotografia è A nella posizione del primo riquadro e B nella posizione del quarto riquadro, ossia tra loro sembra proprio che la distanza sia quella disegnata in azzurro.

Albertino è distrutto, mentre i due fotoni sono ancora un po’ frastornati, ma stanno capendo tutto e sanno anche come fare per ottenere il loro sogno. Lo dicono subito ad Albertino e anch’egli si rincuora. L’accorciamento del righello esiste davvero e può essere misurato, ma la sua visione apparente è ben diversa dalla realtà misurata.

I due amici propongono ad Albertino di fare di nuovo l’esperimento, ma facendo andare il righello alla stessa velocità, ma in verso opposto. Albertino ha ormai capito anche lui e la sua bocca si curva in un sorriso. Come ormai previsto, la nuova foto dà un risultato del tutto opposto: il righello si è accorciato moltissimo ed è addirittura più corto di quanto previsto e misurato da Albertino (Fig. 4). Ma ormai tutti e tre hanno capito il perché e il percome e non possono che brindare tutti assieme con un bel bicchiere di vino (non accorciato…).

Parliamo seriamente e capiamo che una cosa è misurare e un’altra cosa è vedere…

La realtà apparente e quella misurata

La teoria della Relatività Ristretta non è certo “distrutta” da questa favola reale inventata da quei mattacchioni dei fotoni. Tutto, in fondo, si basa sulla “finitezza” della velocità della luce che può dar luogo a configurazioni istantanee nella vita quotidiana, ma che non sono più tali se le distanze da percorrere sono ben più grandi. In generale, abbiamo già dimostrato che fotografare oggetti in movimento (anche non rapidissimo) comporta un visione apparente ben lontana dalla realtà dei fatti, allorché la luce prima di giungere a noi dia il tempo ai vari oggetti di spostarsi in modo evidente.

Tuttavia, anche oggetti posti vicini a noi possono dar luogo a configurazioni del tutto inaspettate, se le velocità con cui si spostano diventano comparabili con la velocità della luce. In modo analogo a prima, nel tempo che la luce impiega per partire da un punto di un oggetto e giungere alla macchina fotografica, l’oggetto stesso si è spostato macroscopicamente e la luce che deve giungere alla macchina, da un altro punto dell’oggetto, allo stesso tempo t₀, proviene da una posizione ben diversa da quella originaria. In fondo è ciò che abbiamo mostrato con la favola. Il fotone che vuole arrivare insieme all’amico deve partire dopo e questo tempo si allunga se si è allontanato a grande velocità dal punto originario. Ciò che fotografiamo al singolo tempo t₀ corrisponde a due fotoni partiti in tempi decisamente diversi.

Abbiamo, perciò, un qualcosa che si aggiunge agli effetti della RR per quanto riguarda l’apparenza visiva (o meglio fotografica) delle dimensioni di un oggetto. Siamo sempre in ambito relativistico, ma certi risultati teorici ineccepibili vengono profondamente trasformati nella realtà visibile.

Il caso del righello è solo il primo e più semplice esempio di deformazione apparente di una lunghezza. Abbiamo visto che deriva dalla finitezza della velocità della luce, ma intuiamo facilmente anche che la deformazione è fortemente dipendente dalla direzione della velocità dell’oggetto rispetto alla macchina fotografica. In qualche modo, possiamo concludere che la lunghezza del righello è estremamente variabile e non è certo quella che ci aspetteremmo dalla RR. Va, quindi, capita bene la differenza.

La contrazione delle lunghezze rimane un dato di fatto che non viene minimamente scalfito. Se in un sistema di riferimento in quiete eseguo le misurazioni atte a stabilire la lunghezza del righello, non posso che confermare una contrazione che dipende solo e soltanto dalla velocità v dell’oggetto (come dimostra il fattore di Lorentz). Tuttavia, se mi chiedo quanto questo effetto misurato sia realmente visibile non posso che accettare una risposta ben più complessa. La macchina fotografica è una prova inconfutabile, dato che essa ci mostra ciò che realmente si vede, comprese le deformazioni di cui si diceva prima.

Sembrerebbe una discussione poco utile se ci limitassimo a misurare la vera differenza tra due punti. Tuttavia, a volte e soprattutto con la tecnologia odierna, è proprio la fotografia che ci dona l’informazione che si deve studiare. Immaginiamo una particella che viaggi a grandissima velocità. Non è certo possibile misurare le sue dimensioni in modo standard, ma solo attraverso una serie di immagini riprese da sofisticate telecamere o da fotogrammi istantanei, fortemente influenzati dalle deformazioni che abbiamo appena cominciato ad analizzare. Lo stesso Einstein non le aveva considerate…

Una trattazione analitica

Descriviamo analiticamente il nostro caso, utilizzando un metodo basato, essenzialmente, sul solo teorema di Pitagora (ma ne esistono sicuramente di alternativi che sfruttano la trigonometria). Tuttavia, quello descritto è sicuramente il più facile da seguire ed è facilmente applicabile nei casi pratici, dato che si riduce a un’equazione di secondo grado…

Consideriamo la Fig. 5. Tracciamo da M la circonferenza che passi per la posizione di A e per quella di B all’istante t in cui deve lanciarsi anche lui. Questa circonferenza ci dice che al tempo t BM è uguale ad AM: i due fotoni arriveranno insieme in M al tempo t₀. Questa uguaglianza ci garantisce l’arrivo contemporaneo, imponendoci le condizioni perché ciò avvenga. In questo contesto l’unica incognita è il tempo t.

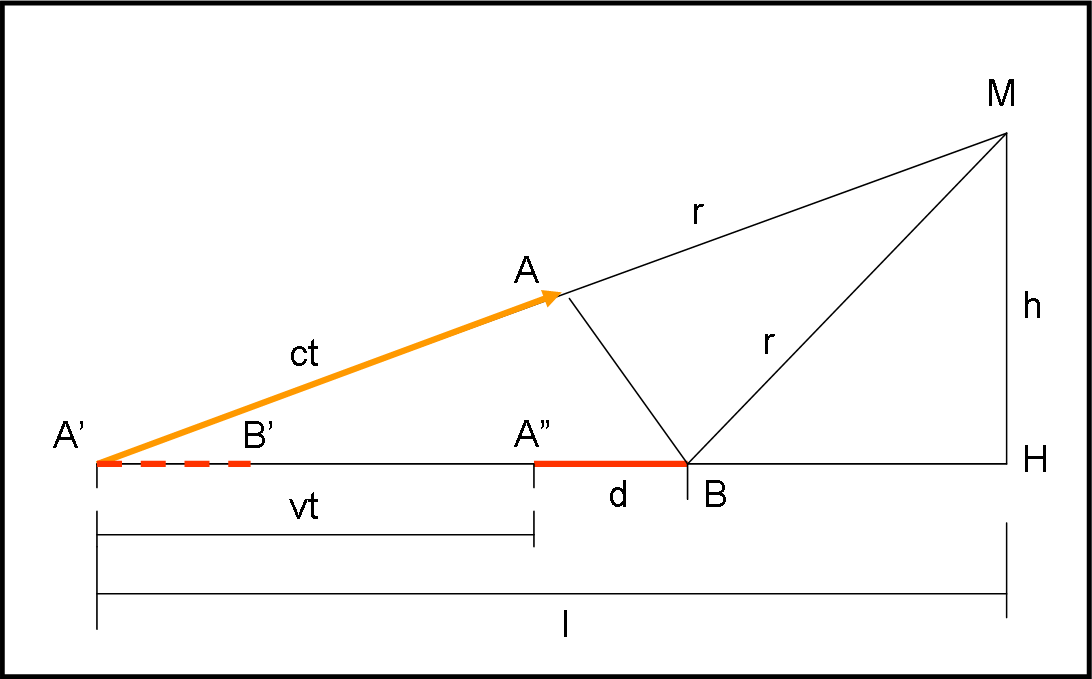
Consideriamo come origine il punto A’ da cui è partito A. Indichiamo con l e h l’ascissa e l’ordinata di M (l’asse delle ascisse è quello su cui si muove il righello di lunghezza d, già contratta).

Al tempo t, il fotone A  ha percorso una distanza che è data da:

A’A = c t

Deve ancora percorrere la distanza AM che indichiamo con r.

Ne segue che:

r = (l² + h²)^1/2 – ct

r² = l² + h² + ct² - 2 ct(l² + h²)^1/2       …. (1)

Nello stesso tempo t il righello si è spostato di vt e possiamo scrivere:

A’H = l = vt + d + BH

E ancora:

BH = l – vt – d

Da cui, applicando Pitagora al triangolo MHB:

r² = h² + (l – vt – d)²

r² = h² + l² + v²t² + d² - 2vlt - 2ld + 2vdt            …. (2)

Uguagliando la (1) e la (2), si ottiene:

l² + h² + ct² - 2 ct(l² + h²)^1/2  =  h² + l² + v²t² + d² - 2vlt - 2ld + 2vdt

Con facili passaggi (e qualche semplificazione), si ha:

ct² - 2 ct(l² + h²)^1/2  =  v²t² + d² - 2vlt - 2ld + 2vdt

t²(c²- v²)  - 2 tc (l² + h²)^1/2 + 2vlt -  2vdt  + 2dl – d² = 0

t²(c²- v²)  - 2 t [c(l² + h²)^1/2 – v (l – d)]  + 2dl – d² = 0

Sostituendo i valori noti è facile trovare la soluzione accettabile di t

Noto t, è immediato ricavare la lunghezza apparente d’, fotografata:

d’ = A’B = v t + d

In modo analogo si può calcolare la contrazione, nel caso in cui la velocità abbia verso contrario.

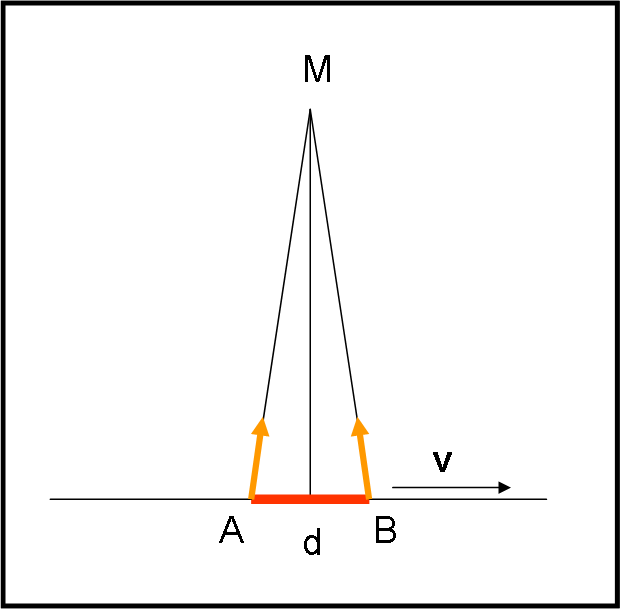
Come potremmo fare per “fotografare” veramente la contrazione di Lorentz e fare contento Albertino? Basta che il righello passi a grande velocità in direzione perpendicolare alla macchina fotografica. Nell’istante in cui si forma l’angolo di 90°, A e B possono lanciarsi insieme verso M, rendendo felice Albertino (Fig. 6).

Abbiamo visto che il quiz ha destato molto interesse. Alcuni ci sono arrivati prima, altri dopo e altri sono rimasti ancora in sospeso… Questa soluzione ha visto l’aiuto fondamentale di Arturo che ha preparato le animazioni che seguono, che mi sono sembrate le più facili da comprendere, oltre ad aver affrontato la parte analitica. Un grazie a tutti, ma a lui in particolare.

Animazioni

Righello fermo (ovviamente non contratto)

Righello già contratto in moto con velocità v (si avvicina a M)

Righello già contratto in moto con velocità – v (si allontana da M)

Non crediate, però, che la storia sia finita qui! Questa è stata la parte più facile, la prossima volta sarà già leggermente più difficile. Leggete quindi con attenzione questa favola molto seria in modo da proseguire con il piede giusto…

Nota fuori dal coro: visioni apparentemente distorte sono, però, frequentissime anche nel mondo comune. Pensiamo alla visione prospettica: lunghezze più lontane si vedono apparentemente più piccole, così come le rotaie sembrano incontrarsi all’infinito. Un’apparente deformazione dell’oggetto che si fotografa dipende, ancora una volta, dal punto da cui viene fotografato. Se un righello viene spostato in varie direzioni, cambia naturalmente la sua lunghezza apparente. Tutto ciò pur restando nell’ambito della fisica classica. Un cubo fotografato assumerebbe forme inaspettate se non avessimo già nel cervello una certa conoscenza delle sue forme previste. Non per niente, quando l’arte è riuscita a capire le leggi matematiche che permettono di costruire queste deformazioni, è riuscita a rappresentare la realtà visiva delle tre dimensioni su un piano. Masaccio insegna…

Ruotiamo il righello

Ruotiamo il nostro righello rispetto alla direzione del moto e vediamo cosa succede. La difficoltà cresce un pochino, dato che dobbiamo disegnare in tre dimensioni, ma chi ha capito la prima parte non avrà problemi a risolvere anche questa seconda parte. La possiamo considerare di “preparazione” a qualcosa di più articolato.

Consideriamo la Fig. 7, dove il righello è sempre lo stesso dell’altra volta e lo possiamo considerare di spessore “nullo” (in poche parole non subisce contrazioni relativistiche). Questa volta utilizziamo due macchine fotografiche che lo fotografino interamente a un certo istante t (può essere anche diverso tra la macchina M₁ (t₁) e la M₂ (t₂)). Il righello AE sta nel piano a e inizia a muoversi a velocità costante relativistica verso M₁. Il righello è posto perpendicolarmente alla direzione CM₁ ed è AC = CE. I punti B e D sono punti medi tra A e C e tra C ed E, rispettivamente (possono essere utili per le varie costruzioni e potete anche usarne di più…). La macchina fotografica M₂ è situata nel piano b perpendicolare al piano a. La configurazione è ben visibile e comprensibile nella figura . Il righello si muove a partire dalla posizione disegnata, al tempo t = 0, con velocità costante v. Le due macchine fotografiche hanno un grandangolo e le rette r e s sono i loro assi ottici.

 

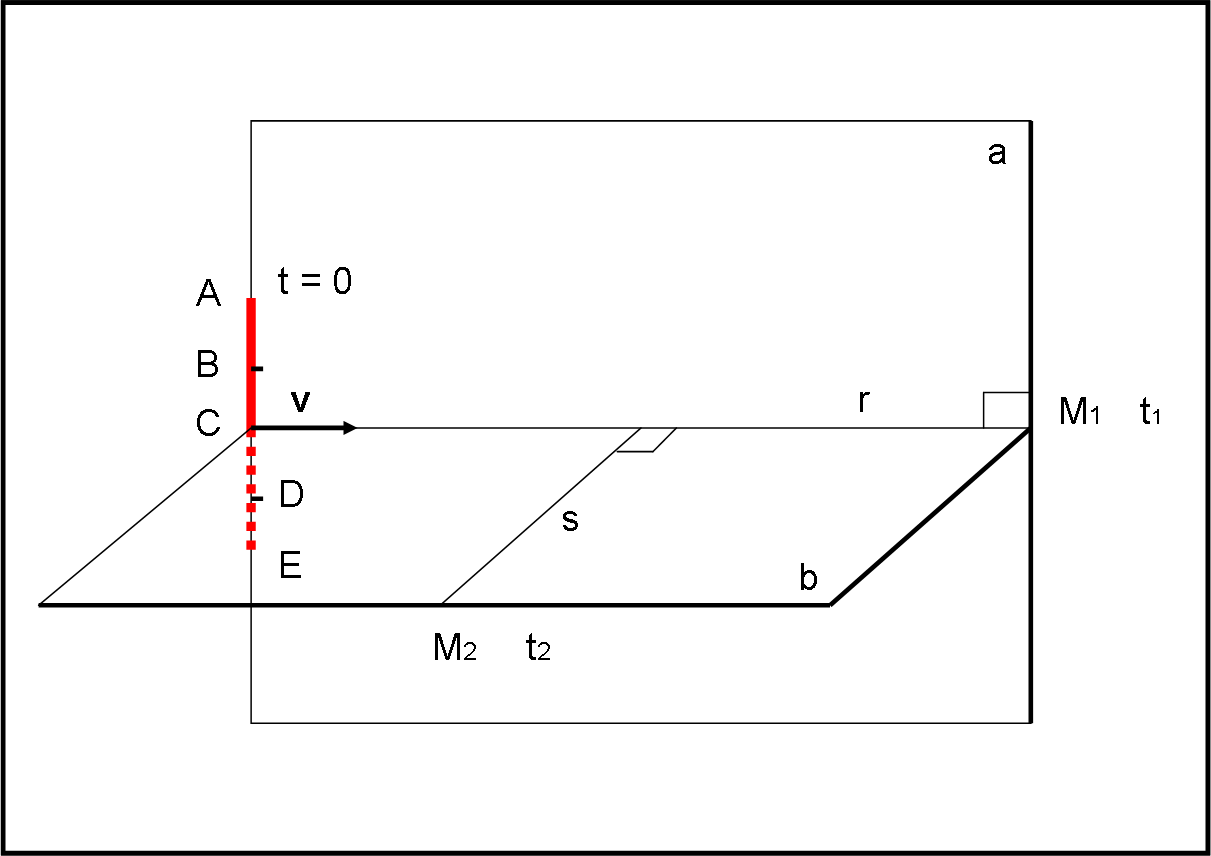
Dato che il  questa trattazione è solo  un punto di passaggio verso una costruzione più laboriosa e forse meno intuitiva, diamo una risposta abbastanza qualitativa, lasciando i calcoli esatti solo a chi avesse proprio voglia di “toccare con mano”. D’altra parte Arturo ha già indicato la strada da seguire nei commenti (QUI).

Ovviamente, la strategia è sempre lo stessa utilizzata per il righello posto in posizione orizzontale : tutto si riduce a definire gli istanti in cui i punti del righello devono inviare i loro fotoni affinché essi arrivino sulle macchine fotografiche M₁ e M₂ ai tempi t_o e t₂

Facciamo allora muovere con velocità relativistica il nostro righello. E’ chiaro, ormai, che i punti A ed E, i più lontani da M₁, devono inviare per primi il loro raggio di luce. I fotoni (che ci interessano) partono dagli altri punti del righello non appena la distanza tra i punti e M₁ è perfettamente uguale a quella che manca ai fotoni di A ed E per giungere su M₁. In altre parole, questi sono i fotoni che riescono ad arrivare simultaneamente in M₁ al tempo t₀.  L’ultima a partire è, ovviamente, la luce emessa da C, il punto più vicino a M₁.

La Fig. 8 mostra ciò che succede, ma è molto più esplicativa l’animazione preparata da Arturo, più immediata che non quella, parimente ben fatta, di Paolo.

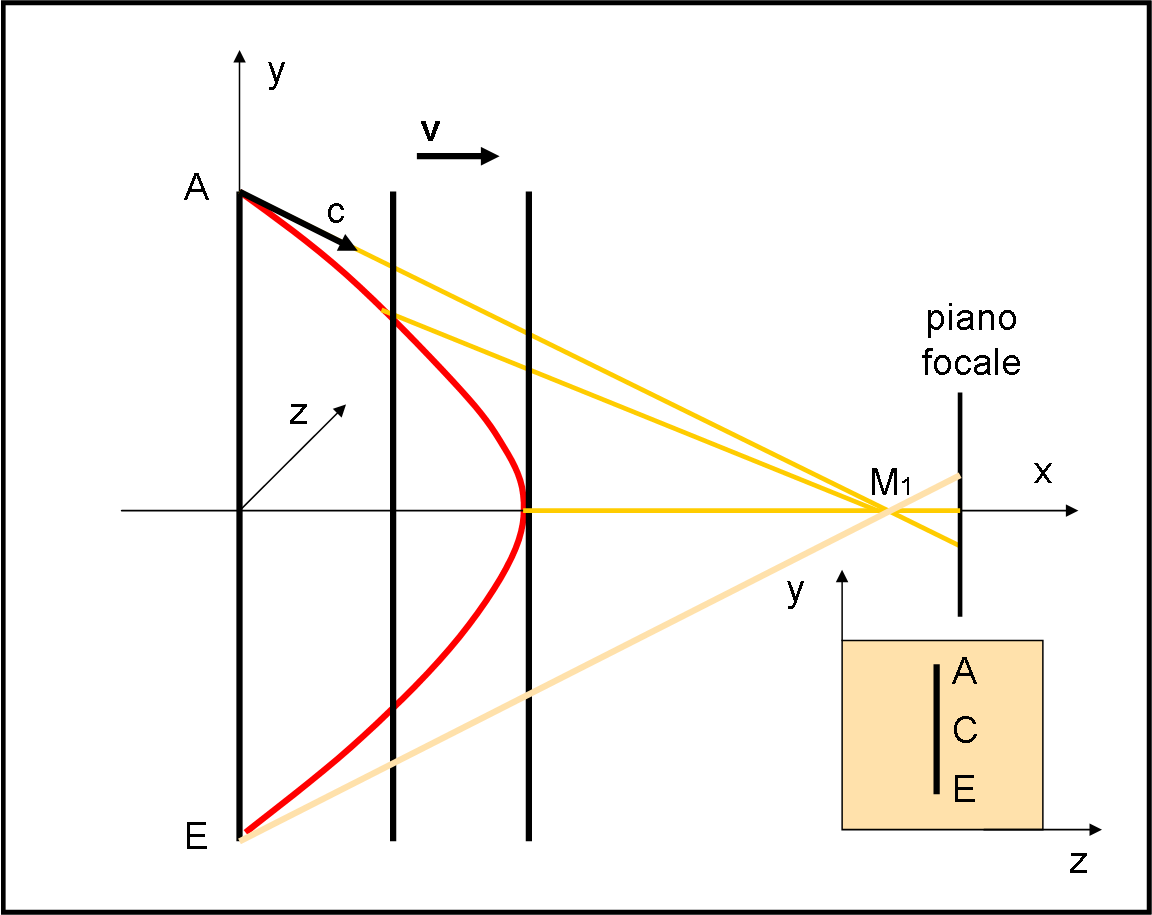
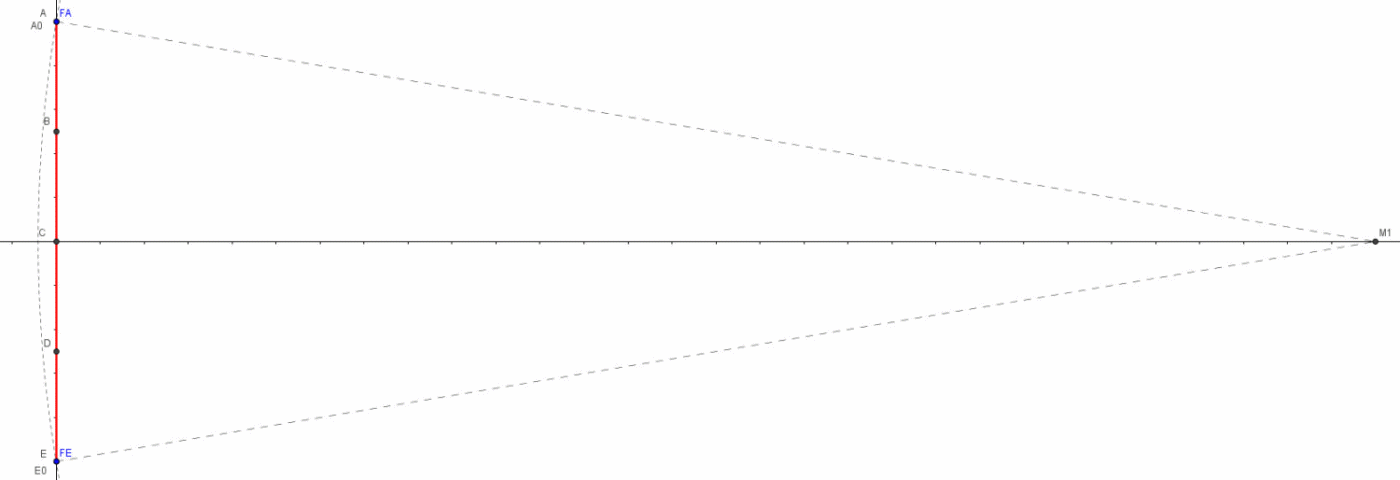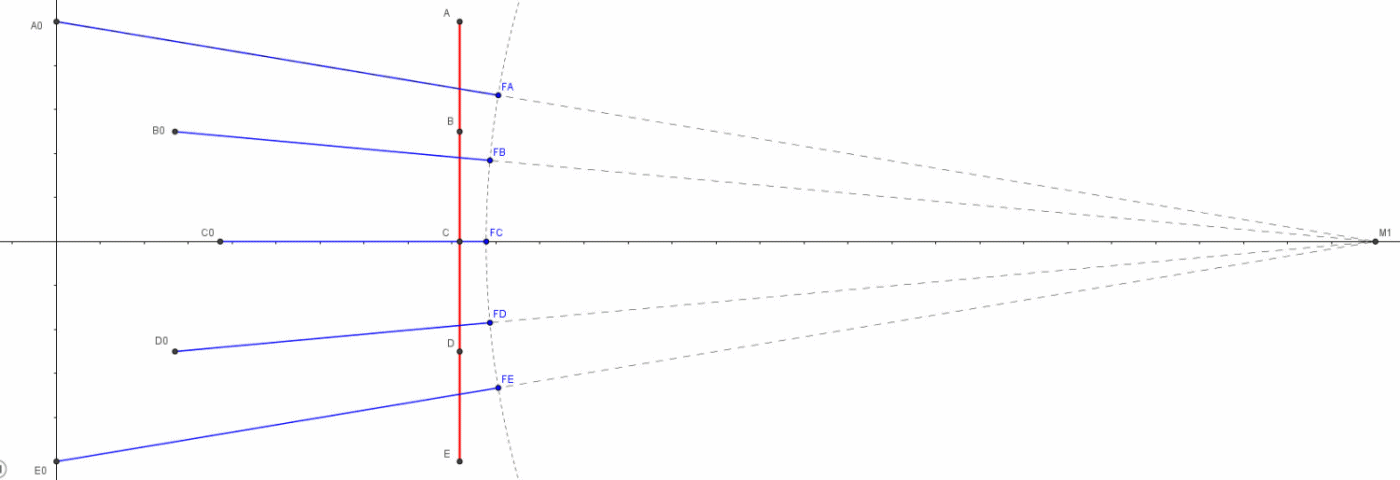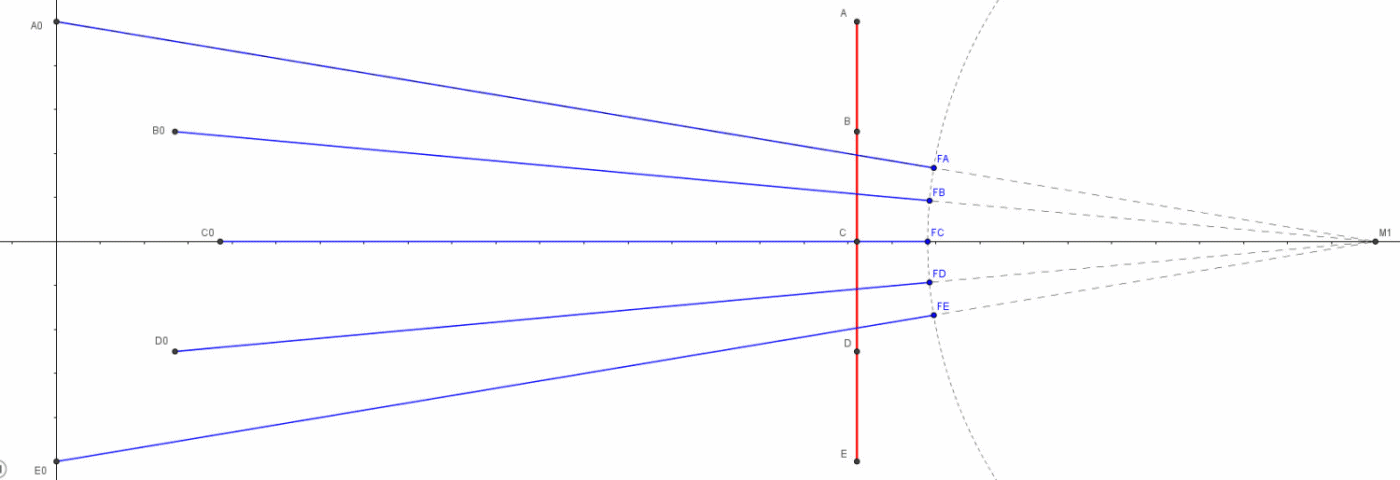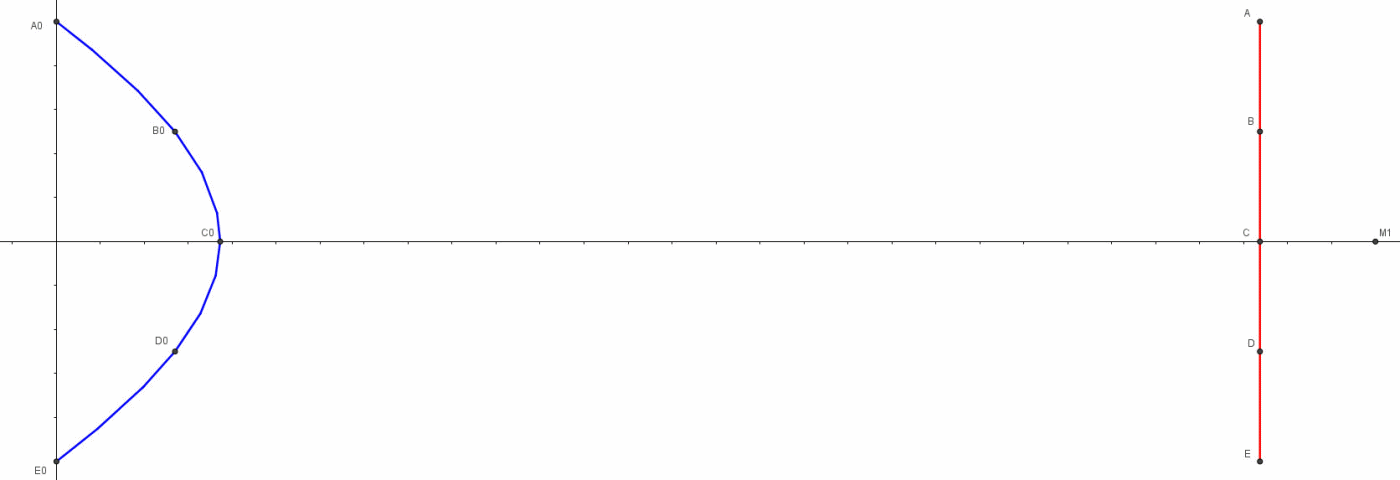
I punti che mandano i loro fotoni in tempi diversi, ma tali da farli arrivare tutti assieme in M₁, descrivono una curva che ha il vertice in C. I punti sono sempre punti dello stesso righello: ciò che cambia è il momento in cui consideriamo l’invio della loro luce e quindi, dato che il righello si avvicina a M₁ con velocità v, essi sono relativi a posizioni sempre diverse del righello. Data la simmetria della figura (l’asse ottico di M₁ passa per il punto di mezzo del righello ed è anche la direzione del moto), si ha sempre una coppia di punti da cui la luce parte simultaneamente, uno sopra e uno sotto all’asse ottico CM₁, come A ed E, B e D, e così via. Solo il punto C rimane singolo e ultimo nell’inviare la luce che ci interessa.

Che tipo di curva è quella che caratterizza i vari punti di partenza della luce dalla sbarra in modo che arrivi a un tempo prefissato nelle macchine fotografiche? Senza svolgere i calcoli (non difficili, ma un po' noiosi) si trova che essa è un ramo di iperbole, di cui M₁ è uno dei fuochi.

 

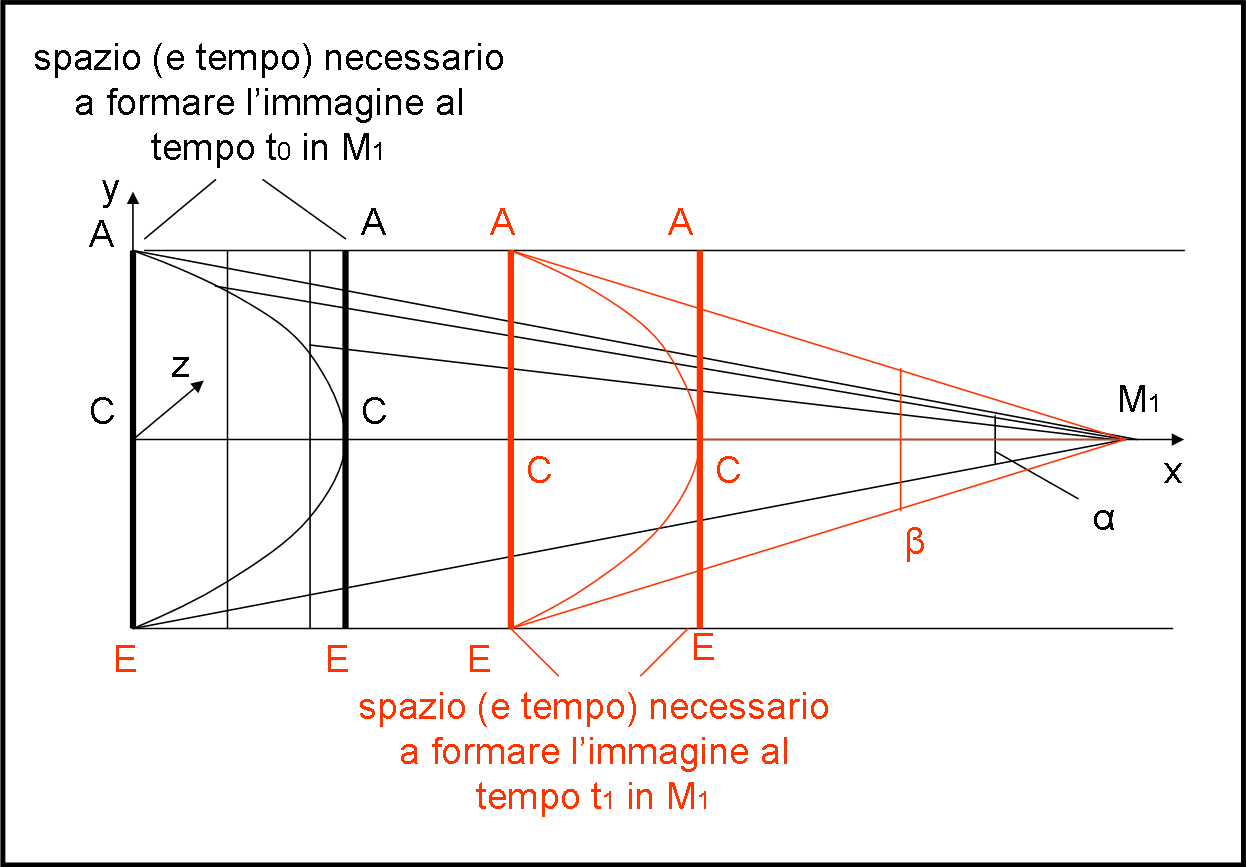
A noi  interessa, ancora di più, sapere cosa fotografa M₁. Dato che il suo asse ottico è proprio quello della direzione del moto (asse x), a sua volta perpendicolare al righello, ciò che colpisce il piano focale non riesce a evidenziare l’ascissa dei punti di invio. Può solo identificare la loro ordinata, ossia la distanza dal punto centrale C. In poche parole, alla macchina M₁ non interessa assolutamente niente dell’iperbole! Ciò che impressiona la sua pellicola -o quello che preferite- è una linea perfettamente verticale, come disegnato nel riquadro piccolo (piano yz) inserito vicino a M₁ nella Fig. 8. Che il punto centrale abbia inviato la sua luce dopo quella inviata dagli estremi A ed E non può cambiare l'immagine di ciò che giunge tutt’assieme sulla macchina fotografica. La distanza angolare tra A e E resta sempre la stessa ed è, ovviamente, uguale a quella visibile da M₁ all’atto della partenza del righello.

Mettiamo, però, bene in chiaro una cosa: ciò che stiamo raffigurando è relativo a un solo istante t0. Se la macchina fotografica facesse un'altra foto al tempo t₁ > t0, avremmo una diversa lunghezza dell’immagine del righello, dato che esso si è avvicinato, come mostra la Fig. 9 (aumenta la dimensione angolare).

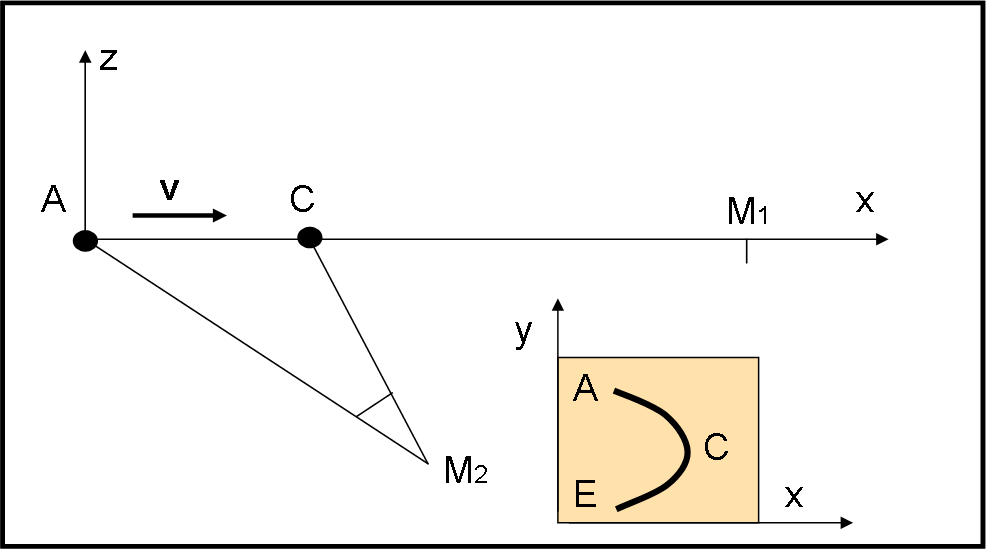
Veniamo brevemente a M₂. Vediamo la situazione dall’alto (Fig. 10), ossia lungo l’asse y. Il righello è un punto che indichiamo con A. In quel momento parte il suo fotone che giunge in M₂ insieme a quello che parte da C in un tempo e in una posizione diversa. Ne segue che nella foto (piano xy) si vede l’iperbole prima descritta. La sua forma dipende molto dalla posizione di M₂, ma su questo punto ci torneremo più avanti.

Digeriamo bene questa parte e prepariamoci a qualcosa di un po’ più complicato e di più “concreto”.

Il righello si sposta e si moltiplica

Non prendetevela troppo con il nostro righello … lui, in fondo ce la mette tutta per creare qualche gioco di prestigio divertente, in collaborazione con la lentezza atavica dei fotoni. Questa volta prima lo spostiamo e poi lo moltiplichiamo per ottenere qualcosa di più complesso.

In altre parole, ci permette già di costruire la nostra prima figura completa (un quadrato formato da righelli).

Consideriamo la Fig. 11, dove abbiamo posto i tre assi cartesiani a partire dal centro del piano focale della macchina fotografica M (ma possiamo scegliere l’origine che vogliamo).

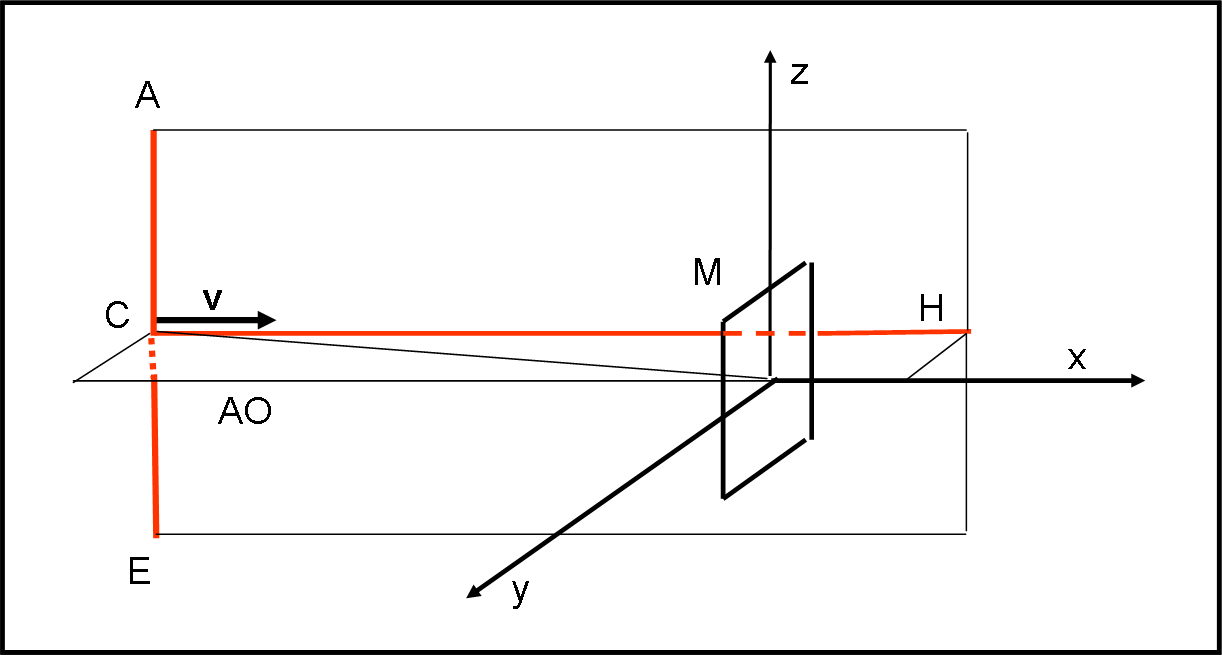
Due parole su quest’ultima… Malgrado sia sofisticatissima si basa essenzialmente sul concetto che si perde nella notte dei tempi della camera oscura, ossia una scatola con un piccolo forellino al centro di una faccia, da cui entra la luce inviata dall’oggetto che si vuole riprendere. Tralasciando i concetti più tecnici, il tutto è facilmente schematizzato nella Fig. 12.

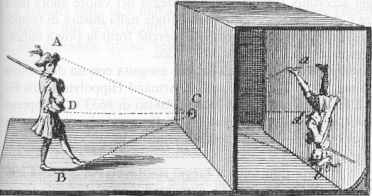
Si forma un’immagine rovesciata dell’oggetto “fotografato”. Se, al posto del forellino, si mette qualche lente scelta ad hoc (obiettivo) è possibile migliorare di molto l’immagine finale e, soprattutto, eliminare il ribaltamento. Nel seguito delle nostre trattazioni consideriamo camere oscure semplicissime, ma, immaginiamo che sia annullato il ribaltamento della figura sia in senso verticale che laterale.

Aggiungiamo ancora che l’asse ottico AO, perpendicolare al piano dove si forma l’immagine, comanda ciò che vediamo, dato che tutto viene proiettato su un piano perpendicolare a lui.

Facciamo un esempio in Fig. 13.

Essa illustra bene come ciò che viene fotografato corrisponde alla proiezione AB’, anche se la luce arriva realmente da A e da B. In poche parole, siamo interessati all’angolo visto dal foro (obiettivo) della camera. La visione di M è una visione giocoforza piatta! In Fig. 3, AB è un oggetto fermo, ma le cose non cambiano se lo mettiamo in movimento ultrarapido: ciò che cambiano sono i fotoni che raggiungono la camera a un tempo prestabilito (o meglio, i loro tempi di invio), ma la camera si interessa solo della loro direzione e della relativa proiezione sul piano perpendicolare all’asse ottico.

Torniamo alla Fig. 11. Il nostro righello AE è stato spostato, in modo che resti sempre perpendicolare al piano (x,y), ma in modo che il suo moto avvenga lungo una retta parallela all’asse ottico AO (ossia CH) che coincide con l’asse x.

La macchina M vede, quindi una proiezione su un piano parallelo al piano (z,y). Facciamo pure partire il nostro righello AE con velocità relativistica v.

Cosa viene impressionato sul piano focale, ricordando che abbiamo eliminato qualsiasi ribaltamento? La risposta è già insita nella soluzione precedente.

Vediamo subito la Fig. 14, che lo rappresenta. L’asse x è l’asse ottico AO della macchina fotografica M, mentre il righello si muove lungo CC’. Sappiamo già che il righello si deforma assumendo la forma di un’iperbole, disposta sul piano AA’E’E, dato che la luce di C deve partire in C’ per poter raggiungere, nello stesso istante di A ed E, la macchina M. Fin qui conosciamo già il gioco.

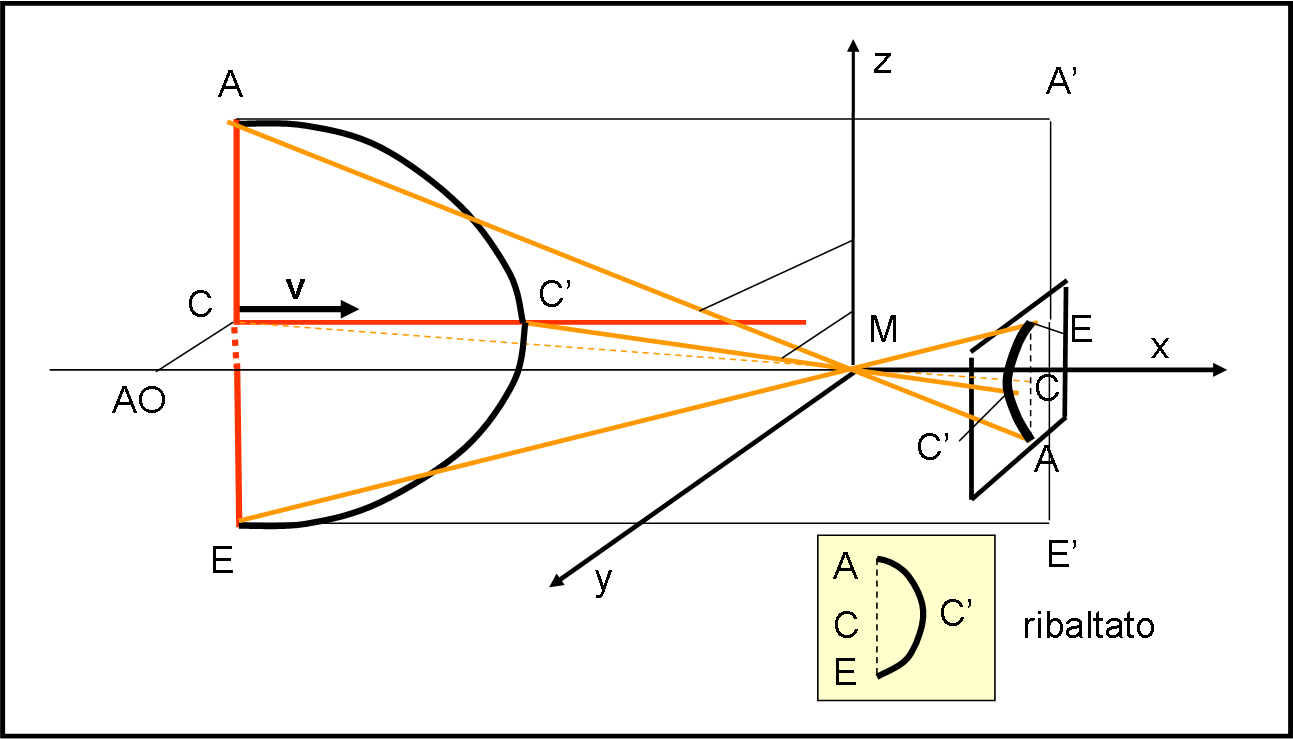
Adesso, però, vediamo tutto “fuori asse del moto” e quindi dobbiamo tenere conto dell’angolo sotto cui M vede A ed E (prima luce partita)  e poi C’, rispetto all’asse z (ad esempio). Quest’ultimo è maggiore e quindi nel piano focale C’ si sposterà lateralmente rispetto al segmento AE. Abbiamo detto che il nostro obiettivo è capace di ribaltare l’immagine ottenuta dalla camera oscura e, in conclusione, ciò che apparirà nel piano focale è un segmento curvilineo con C’ spostato verso destra, ossia verso l’esterno.

In poche parole, è come se vedessimo “di sbieco” l’iperbole descritta nel piano AA’E’E.

A questo punto non resta che costruire qualcosa di più serio… Uniamo quattro righelli e formiamo un quadrato come quello di Fig. 15, dove abbiamo steso una bella tela arancione su di lui. Esso si muove proprio lungo l’asse ottico con velocità relativistica v.

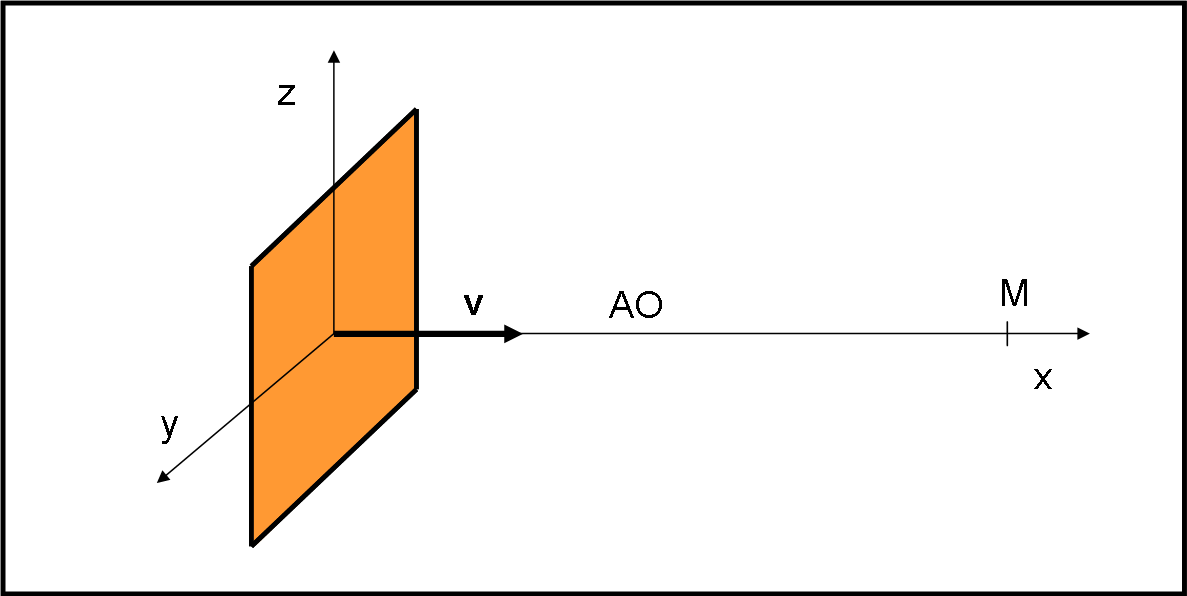
Facciamolo partire da lontano e prendiamo vari scatti in tempi diversi fino a che non arrivi molto vicino a M. Gli scatti, ovviamente, sono tutti relativi all’arrivo dei raggi dell’intero quadrato sulla camera M, in un certo tempo prestabilito (come fatto finora).

Si potrebbe  anche spostare il quadrato e farlo muovere lungo un’asse parallelo a quello ottico (Fig. 16) e mostrare cosa vede la macchina M …

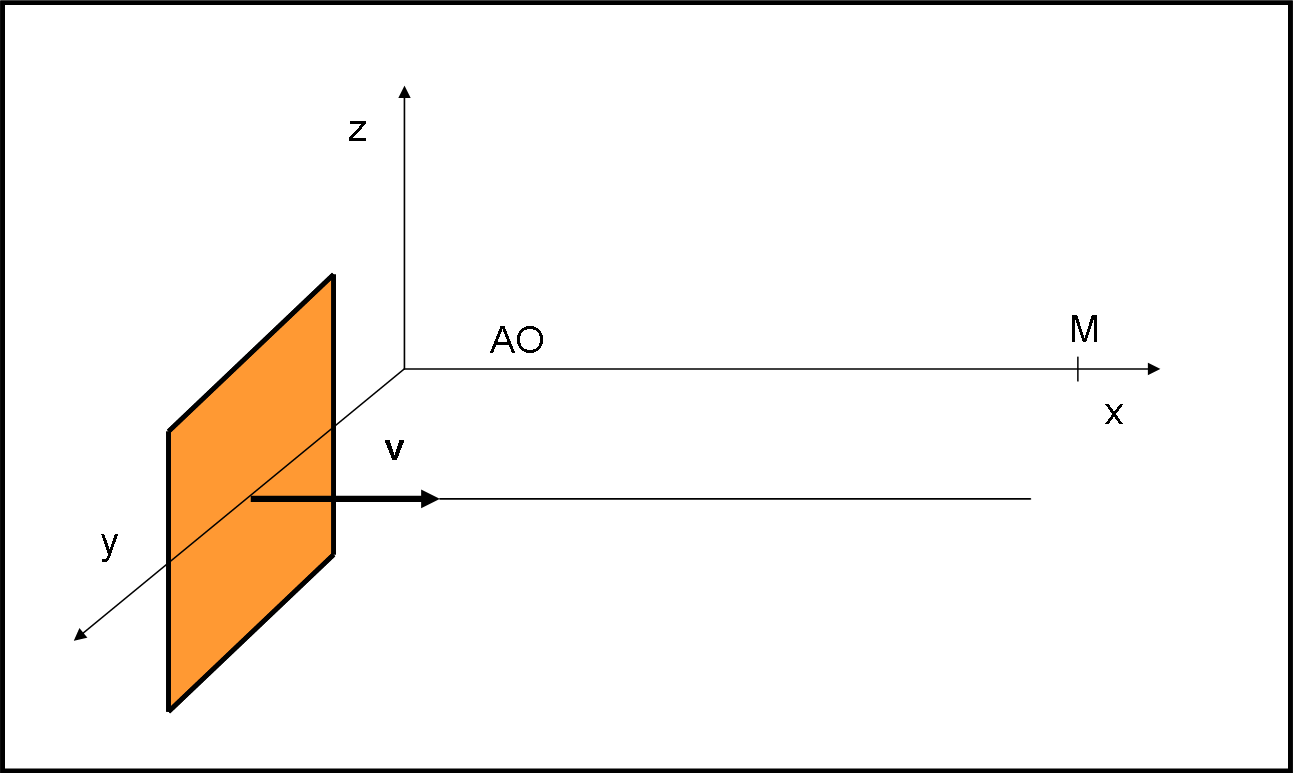
Se la velocità della luce fosse di 130 km/h sarebbe la visione normale che avremmo ai bordi di un’autostrada!

Di tutta questa parte non pretendiamo certo una trattazione analitica, ma solo una descrizione qualitativamente esatta, che spieghi il perché dei vari risultati.

 

Ogni righello del quadrato si comporta come quello singolo (spostato rispetto all'asse) appena studiato, in modo anche quantitativamente simile, data la simmetria dei lati del quadrato rispetto all’asse ottico che passa per il suo centro e arriva alla macchina M. Vediamo la Fig. 17. Nascono quattro iperboli, una per lato, tutte uguali tra loro. Ognuna sarà vista di sbieco da M e quindi avrà il vertice spostato verso l’esterno. L’immagine sul piano focale di M è riportata vicino a lei: un quadrato che ha messo su molta pancia (come lo capisco…).

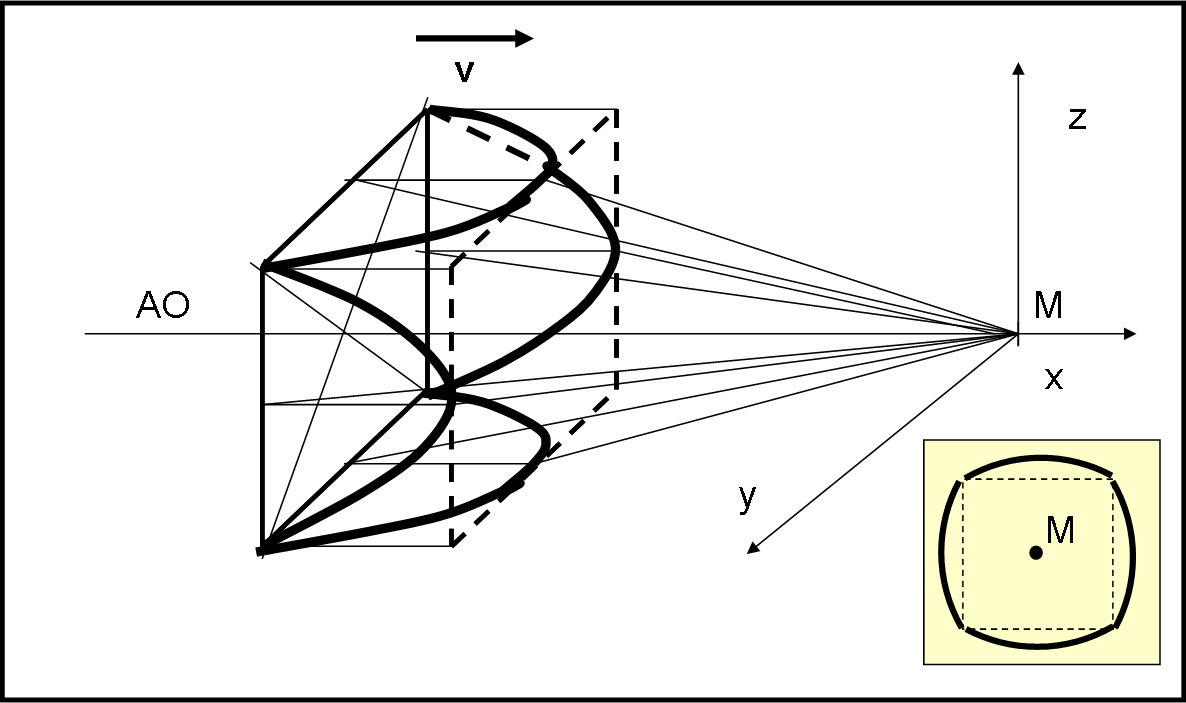
A questo punto possiamo anche inserire tre filmati che fanno vedere come una griglia cubica formata da righelli (un po’ più complicata, dato che abbiamo anche righelli intermedi) si vede da una telecamera posta in M, durante l’avvicinamento e l’allontanamento.

Il primo filmato riprende un avvicinamento a bassa velocità (nessun effetto relativistico, ma solo prospettico).

bassa velocità

Il secondo avviene  con una velocità pari al 90% della velocità della luce (quanto spiegato precedentemente si vede molto bene), in cui è presente anche l’allungamento dei segmenti posti parallelamente alla direzione del moto = asse ottico, capace  di superare la contrazione relativistica e mostrare un effetto opposto. I righelli posti all’interno dei vari quadrati danno luogo a un effetto ulteriore che spiegheremo tra poco.

altà velocità

Il terzo filmato mostra la stessa figura che si allontana con v = 0.9 c. Ovviamente, la concavità dei lati si inverte.

gitter-w0.9-xe-320x240

I filmati sono preparati dalla bravissima Ute Kraus .

La situazione diventa leggermente più complicata se riempiamo di “tela” il nostro quadrato di Fig. 18. In altre parole, non abbiamo solo i righelli laterali e nemmeno qualche righello intermedio (come nei filmati), ma una superficie continua (sottilissima) all’interno del quadrato. Per spiegare cosa succede in modo semplificato, ma sufficientemente corretto, consideriamo la Fig. 18.

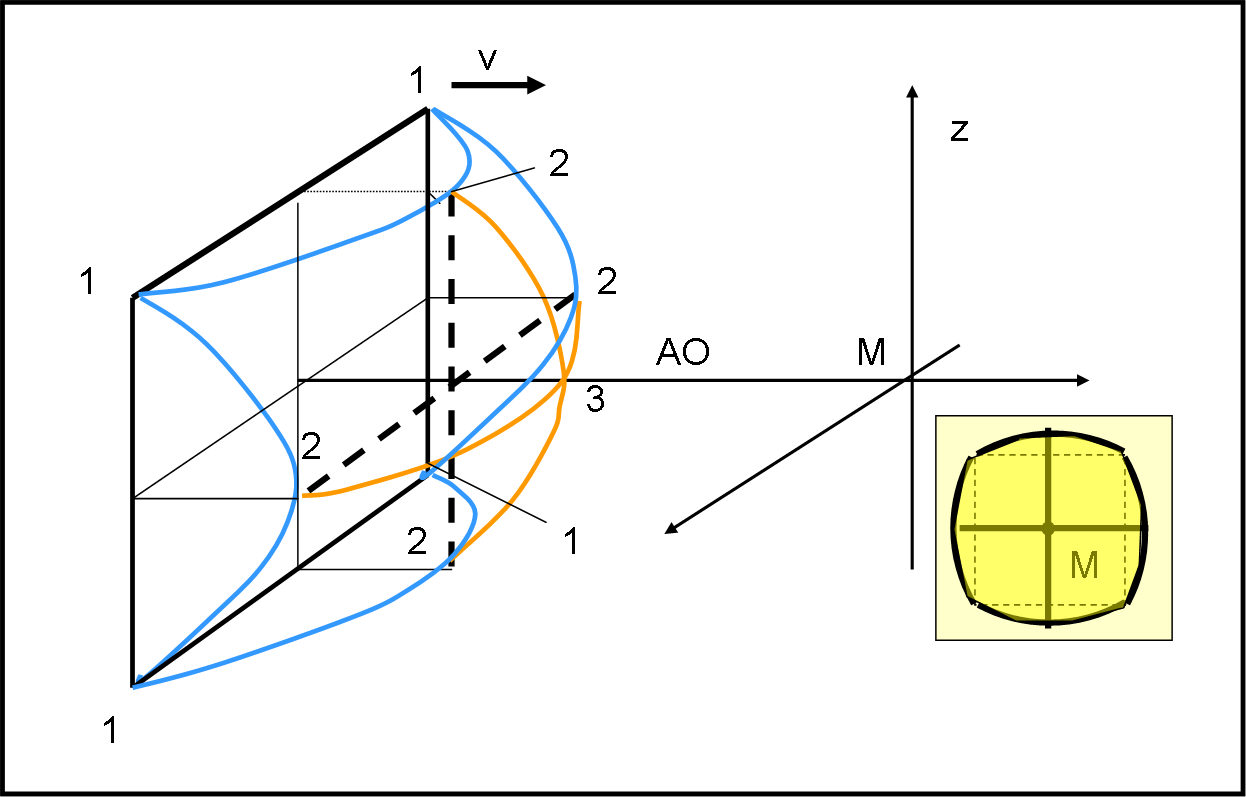
Il perimetro del quadrato corrisponde alla partenza della prima luce. Non tutta insieme, però, da come abbiamo visto precedentemente. Gli spigoli indicati con 1 sono i primi “lanciatori”, seguiti dai punti di mezzo dei singoli lati (indicati con 2). Otteniamo le curve azzurre come già ottenuto con il quadrato vuoto. Tuttavia, quando il quadrato perimetrale è giunto in 2, inizia il lancio della luce dalle parti più interne del quadrato (i loro tragitti per giungere in M sono decisamente minori). Vale la pena considerare solo le due linee tratteggiate relative ai punti di mezzo.

Il loro punto d’intersezione sta sull’asse ottico e corrisponde al tragitto più corto. Ne segue che a partire dai punti esterni della “croce” tratteggiata, si devono disegnare due iperboli che si incontrano nel punto 3, l’ultimo da cui parte la luce. La forma finale del quadrato pieno, vista lateralmente come rappresentato in figura, dà luogo a una superficie iperbolica, dato che ogni sezione ottenuta con un piano perpendicolare al quadrato (e quindi al piano focale) deve dar luogo a un iperbole (come trovato precedentemente).

Una vera e propria vela quadrata al vento, che se vista da M non si discosta molto da quanto visto precedentemente, per il quadrato vuoto. Le iperboli relative alla parte tratteggiata danno luogo a segmenti dato che hanno il loro vertice proprio sull’asse ottico (punto 3).

Ben diversa la situazione se la vela è vista da un punto qualsiasi che non sta sull’asse ottico (non ci vuole molto a immaginarsela). La vela si gonfia per effetto del "vento relativistico" (Fig. 19) e via verso nuove avventure! Mi sembra di vedere i nostri amici fotoni che scrutano il mare di … Dirac.

Ricordiamoci sempre che tutto questo è quello che si VEDE e non quello che si MISURA!!

Una torta che diminuisce e i getti galattici 

Abbandoniamo il nostro righello è dedichiamoci a una superficie sferica. Lo faremo attraverso uno dei soliti scherzi che si fanno i due famosi fratelli Pippo e Pappo.

Un caldo eccessivo può fare venire le “allucinazioni”… Sarà questo il caso descritto nel nuovo problemino che vede coinvolti i nostri “cari” amici Pippo e Pappo? Qualcosa mi dice di no…

Pappo non solo è cresciuto, ma è diventato bravissimo in fisica ed è lui che adesso si diverte a prendere in giro Pippo. E’ anche un piccolo inventore e riesce a fare cose che sembrerebbero assurde nel mondo comune.

La mamma ha preparato un dolce veramente squisito: una sfera di pasta sottilissima, vuota all’interno, tipo bombolone, ricoperta da uno strato di ogni ben di Dio: gelato di fragola, di pistacchio, di banana e di cioccolata al latte. Un mix molto bello a vedersi, che piace molto ai ragazzi. Una sua visione frontale (diretta verso Pippo) e una laterale sono date in Fig. 20.

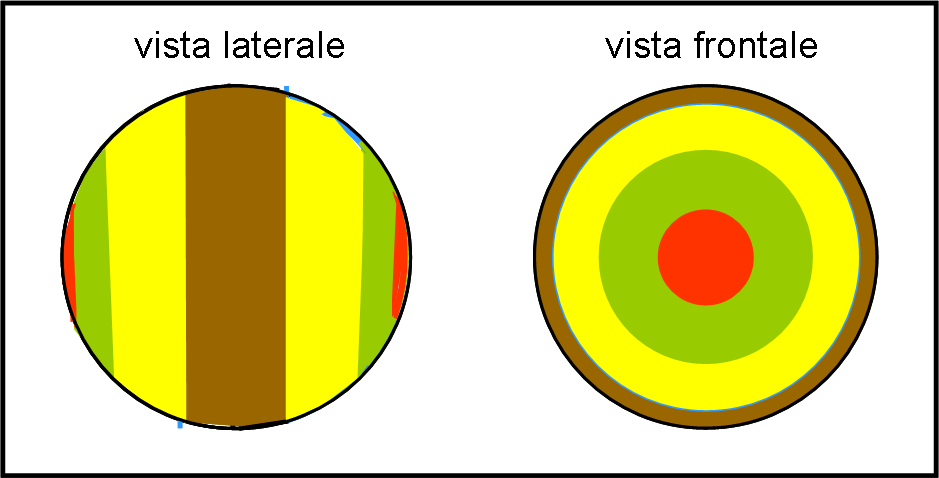
Pappo propone a Pippo un piccolo gioco di prestigio. Lui userà uno dei suoi esperimenti quasi magici e Pippo mangerà solo la parte di torta che riuscirà a vedere. Beh… non essendo troppo vicino al dolce sferico (possiamo immaginarlo posto all’infinito, Fig. 21) la parte che Pippo non riesce a scorgere è del tutto trascurabile e lui vede quasi esattamente metà del dolce sferico. Metà ciascuno, non fa male a nessuno!

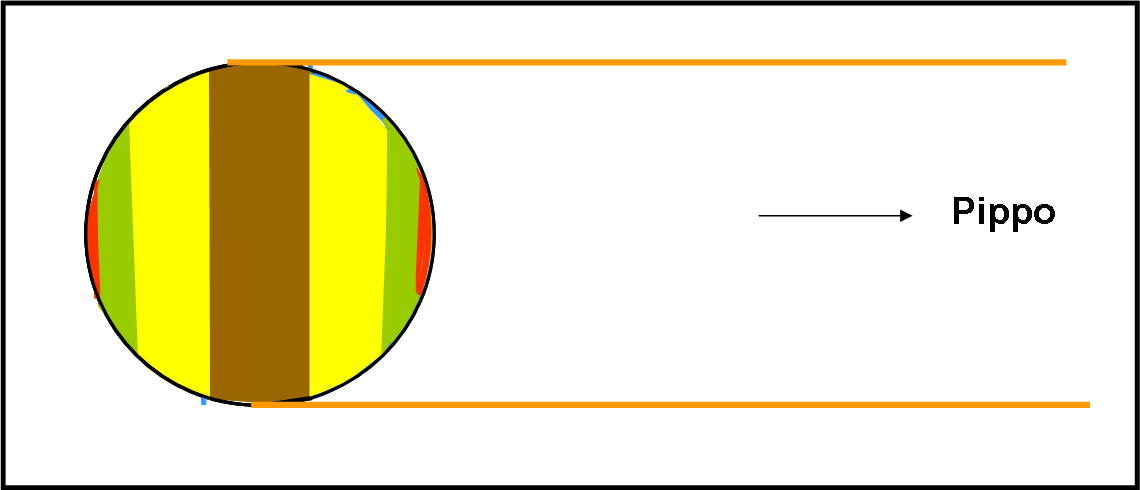
Ma… Pappo continua: “Se, però, tu dovessi vedere solo un singolo colore dei quattro presenti, io mi mangerei tutto il dolce!”. Pippo sa che il fratello è diabolico, ma giudica impossibile l’eventualità prospettata da Pappo e accetta. Per sicurezza, aggiunge: “Guai a te, però, se sposti il dolce (deve rimanere dov’è… non si sa mai…), o se cerchi di modificare manualmente le superfici dei vari colori”. “Perfetto”, dice Pappo “ Ti giuro che non sposterò il dolce e non cambierò i colori”. Poi prosegue: “Solo dopo una frazione di secondo, ossia quando tutti i raggi arriveranno contemporaneamente ai tuoi occhi, potrai darmi una risposta. Sarà bene, però, che tu me la dia in fretta dato che il mio esperimento non può andare per le lunghe." In altre parole, Pippo deve aspettare un attimo, per fare arrivare sia i raggi che partono dalle zone più vicine della sfera sia quelli che provengono dalle più distanti. Quando è sicuro che l'immagine non cambia, può dare la risposta. Deve anche fare in fretta, per altri motivi... tecnici...

Purtroppo, come volevasi dimostrare, Pippo rimane a bocca asciutta… Che magia è riuscito a fare Pappo?

Il quiz non è facilissimo (ci vogliono intuizione e ragionamento) ed è abbastanza imprevedibile. Spero che sia compreso bene. Tuttavia, la soluzione qualitativa (che basta e avanza) abbisogna di una geometria veramente elementare, senza alcuna formula matematica! Chiunque può arrivarci, con un po’ di ragionamento …

Vi posso anche dire che la sua importanza va ben oltre le torte… sferiche, in quanto caratterizza molto bene i getti dei buchi neri galattici!

Inoltre, ricordando le parole di Maurizio, potremmo anche dire che l’illusione (se illusione è) è quanto mai reale e concreta, dato che Pippo rimane senza torta!

Avrete già capito che questi problemi, legati alla visione "apparente" di strutture più o meno semplici che mostrano velocità relativistiche, giocano un ruolo importantissimo nel descrivere come gli effetti della RR (soprattutto la contrazione delle lunghezze) siano completamente deformati quando siano realmente visti o -meglio- fotografati da un osservatore appartenente a un altro sistema di riferimento.

Vi posso dire che questa problematica ha dato il via a molte discussioni, ripensamenti, dispute anche accese, che durano tuttora. Noi andremo avanti mantenendo l’intera trattazione su livelli semplici e comprensibili a tutti, tralasciando le formulazioni matematiche più complesse che hanno coinvolto personaggi del calibro di Terrell e Penrose. Alla fine potremo mettere insieme un argomento poco conosciuto, ma estremamente stimolante e ricco di numerose sfaccettature.

Ma torniamo a noi, dato che la strada è ancora abbastanza lunga. Abbiamo già imparato una cosa fondamentale: la luce, l’informazione regina per conoscere l’Universo, è capace di giocarci tiri mancini, non solo a livello microscopico. Sarebbe molto meglio il “tatto”, attraverso il quale la misura di un qualcosa non sarebbe influenzata dalla lentezza della luce. Sarebbe, ovviamente… ma è del tutto assurdo pensare di credere solo in quello che si tocca, quando le distanze in gioco sono fuori dalla portata di qualsiasi “mano” cosmica. L’esplorazione spaziale e le immagini dei massimi telescopi e dei più accurati microscopi hanno bisogno della luce. Ne segue che quella che sembrerebbe una realtà deformata diventa la realtà con cui dobbiamo scontrarci. Non resta che capire le deformazioni e fare un passo indietro, ma non sempre la faccenda è così banale… anzi!

Un gioco di prestigio diventa la normalità e la normalità il vero trucco da scoprire. D’altra parte la RR ci ha già messo di fronte a situazioni del genere. Pensiamo al muone: lui non potrebbe arrivare a terra e invece ci riesce e ne abbiamo la certezza “pratica”. Una magia che diventa realtà fisica. Immaginiamo di aggiungere a questo fenomeno quasi paranormale, tutti gli effetti dovuti a quei giocherelloni dei fotoni e alla loro velocità di crociera di tutto riposo: se gli oggetti coinvolti avessero dimensioni non trascurabili, la magia apparente supererebbe la magia reale. Un vero caos.

Per darvi un’idea di quanto tutto ciò sia, anche se quasi completamente inosservabile, una pura stregoneria quotidiana, pensiamo a una velocità della luce di soli 30 km/h. Il mondo attorno a noi sarebbe un vero incubo (abbiamo parlato QUI di cosa cambierebbe nella nostra visione dell'Universo, se la velocità della luce fosse diversa da quella che è)

Bando alle ciance (si fa per dire…) e torniamo ai nostri due amici, Pappo e Pippo.

Lo strumento geniale di Pappo non è altro che una specie di “ago” per palloni da calcio, unito a una pompa ancora più speciale. In tal modo (almeno ai miei tempi) si gonfiavano i palloni di cuoio. L’unica vera differenza è che la pompa di Pappo è veramente potentissima e permette al pallone-torta di gonfiarsi, ossia di espandersi, a velocità relativistica. Non sbagliate di certo se pensate all’espansione dell’Universo (il quiz originario l’avevo proprio impostato su questo, ma poi sorgevano difficoltà troppo grandi per mantenere analogie soddisfacenti e non travisanti). Un Universo colorato in modo geometrico…

Capite anche perché è bene che Pippo risponda abbastanza in fretta, altrimenti la torta esploderebbe in mille pezzi! La mamma dei due ragazzi è un'ottima cuoca, ma la sua "pasta" non può competere con lo spazio dell'universo...

L’unico concetto da comprendere fin dall’inizio è che la luce che viaggia verso Pippo deve seguire un andamento orizzontale, mentre la superficie della torta sferica s’ingrandisce radialmente, mantenendo sempre lo stesso centro, ma aumentando il proprio raggio R di un fattore dR = v dt (dove dt è un certo tempo prefissato, ad esempio scelto come unità). Ma tralasciamo del tutto le formule, anche se semplici, e utilizziamo  la semplice Fig. 22.

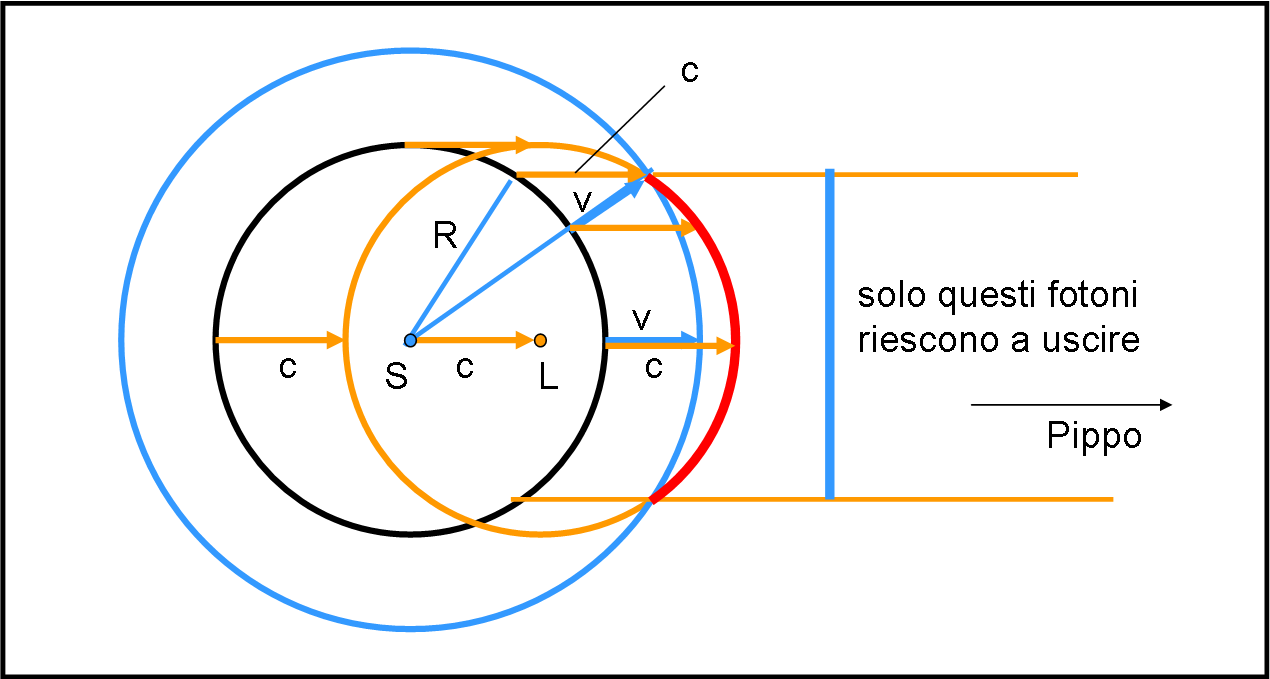
La torta sfera (cava) originaria è il cerchio nero. Pappo inserisce la sua pompa relativistica e permette alla torta di dilatarsi, in un certo tempo dt, fino a diventare il cerchio azzurro. In un tempo unitario (dt = 1) l’aumento del raggio della sfera cava è esattamente dR = v, indicato dalle frecce azzurre. Qualsiasi raggio si consideri, esso si è allungato radialmente della stessa quantità. Insomma la torta nera è diventata la torta azzurra.

Tuttavia, nello stesso tempo dt = 1, anche i fotoni sono partiti dalla sfera originaria. Essi si muovono in senso orizzontale (devono raggiungere Pippo)  di una lunghezza pari a c dt = c = velocità della luce. v è decisamente più bassa di c, ma cosa capita al fotone che parte dal punto più alto della sfera (o da quello più basso)? Per veloce che vada non riesce a raggiungere la parte interna della superficie della torta che si è portata più avanti. In qualche modo, rimane intrappolata dentro alla torta e mai, nel tempo dt, raggiungerà Pippo, ossia Pippo mai riuscirà a vedere quel punto della sfera: nel tempo dt, il fotone sarà sempre indietro rispetto alla superficie della torta.

Ma non è solo quel fotone a subire questa sconfitta… Per generalizzare il tutto in modo immediato, disegniamo un altro cerchio, ossia quello che raffigura la posizione, al tempo dt = 1, dei fotoni lanciati dalla sfera al tempo iniziale. Questo cerchio è di banale costruzione: basta prendere la torta e spostare il suo centro di una lunghezza pari a c (cerchio arancione), come la figura mostra meglio di tante parole.

A questo punto abbiamo a disposizione due circonferenze fondamentali: quella della torta espansa in un tempo unitario e quella relativa al punto di arrivo di tutti i fotoni dopo lo stesso tempo dt = 1.

Come facciamo a vedere quali sono i fotoni che sono riusciti a essere più veloci dell’espansione della sfera? Basta intersecare i due cerchi (azzurro e arancione) e la parte rossa (del cerchio arancione) che rimane più avanti di quella azzurra rappresenta il gruppo di eroici fotoni che si dirigono senza più problemi verso Pippo.

Attenzione: questi fotoni non hanno certo attraversato la torta, ma sono sempre stati avanti rispetto a lei. I fotoni rimasti indietro possono al limite toccare la superficie interna della torta, ma non certo attraversarla. E se toccassero la parte interna... sparirebbero.

Dopo un altro tempo dt = 1, la situazione si ripete tale e quale (è come se prendessimo una torta più grande e ripetessimo l’esercizio). L’importante è considerare i nuovi fotoni inviati dalla torta dopo dt = 1 e non più quelli iniziali che sono già stati “scremati”. Come la faccenda si evolva a noi interessa poco, dato che i fotoni che ci interessano sono quelli del primo lancio.

Una piccola aggiunta… In realtà, i fotoni delle parti più esterne della zona interessata devono partire poco prima di quelli centrali per giungere insieme a loro da Pippo. Poco male… basta solo fare partire un po’ dopo quelli centrali (tanto sono liberi di farlo  dopo un minimo intervallo di tempo, nessuno li ferma) e si aggregano perfettamente a quelli laterali. E’ il nostro righello verticale al contrario… parte leggermente curvo e dobbiamo aspettare che diventi rettilineo. Tuttavia, si può benissimo tralasciare questo effetto di ordine superiore…

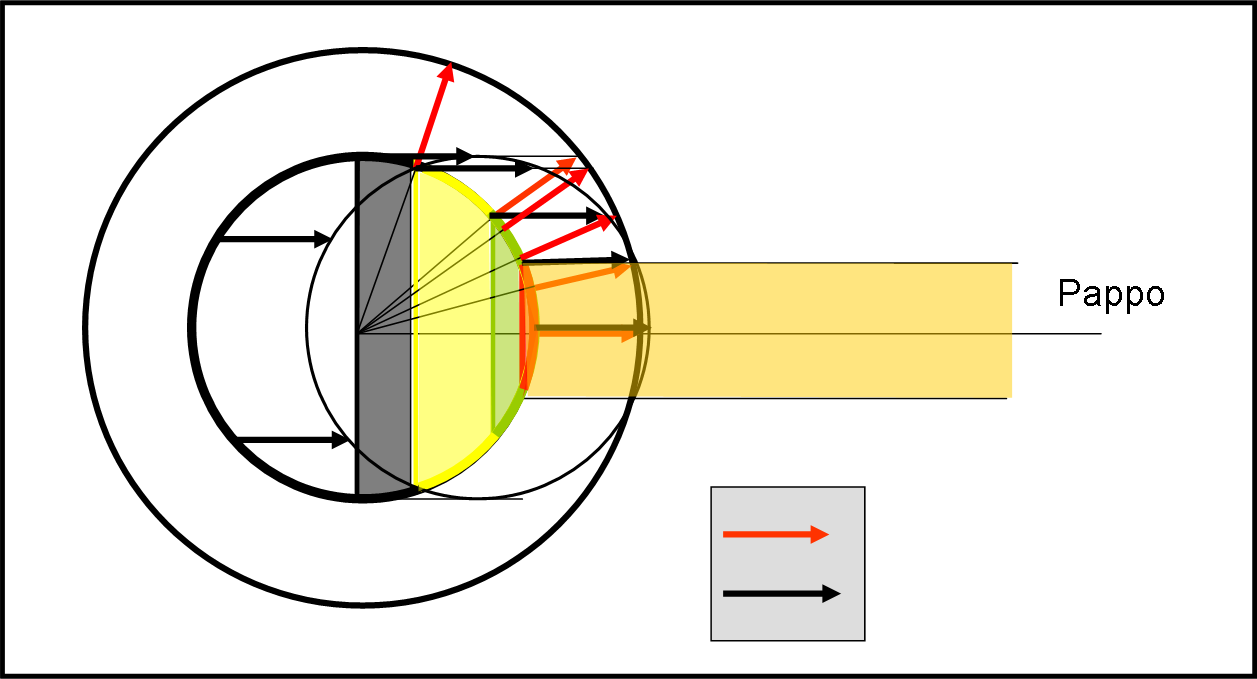
Il succo di tutto è che il nostro Pippo è costretto a vedere solo la parte centrale rossa della torta, dato che i fotoni degli altri colori non riescono a uscire allo scoperto. Quanta parte della sfera sia visibile dipende, ovviamente dalla velocità di espansione. Affinché Pippo rimanga a bocca asciutta è necessario scegliere la v giusta, cosa che Pappo ha saputo fare con grande precisione e che è illustrata in Fig. 23.

Qui di seguito il video di Arturo (che ringrazio apertamente). A noi interessa, ovviamente, solo la prima parte

Risolto il quiz, diamone una interpretazione ben più generale e… astrofisica.

Una sfera, che si espande a velocità relativistiche, viene vista solo parzialmente da un osservatore molto distante (non prendiamolo vicino se no le cose si complicano troppo, pur non cambiando il succo). Ciò che si vede è solo la parte centrale, sempre più piccola al crescere della velocità di espansione. Teoricamente, per v = c, vedremmo solo un punto della sfera. Ho recuperato la bella figura che segue (Fig. 24), che ci mostra con le giuste misure una sfera che si espande a velocità crescenti. Per evidenziare il restringimento della zona visibile, la sfera è stata disegnata a scacchi chiari e scuri. La prima velocità è nulla, la seconda è pari al 70% della velocità della luce, la terza al 90% e la quarta al 99%.

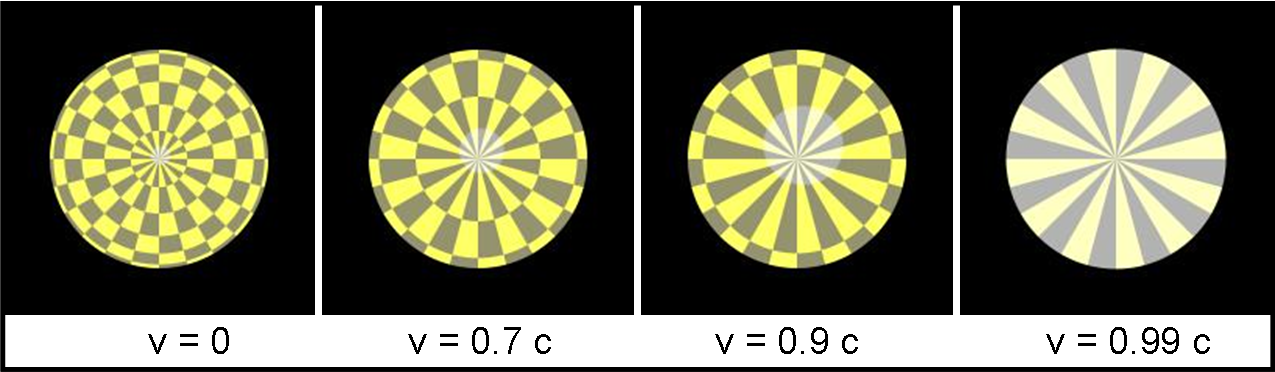
Noterete che vi è anche una zona circolare leggermente più chiara che all’inizio è collocata al centro come una macchiolina e che alla fine copre l’intera parte visibile. Questa macchiolina introduce al discorso sui getti relativistici del buchi neri galattici.

Più o meno sappiamo come si originano, attraverso la caduta della materia del disco di accrescimento verso il buco nero e la sua interazione col campo magnetico (effetto sincrotrone) che serve come lanciatore efficientissimo. Fatto sta che le particelle che li compongono viaggiano a velocità decisamente prossime a quelle della luce. Tuttavia, succede proprio il contrario della torta-sfera di Pappo.

I getti si scontrano con il mezzo intergalattico, si alza la loro temperatura e diventano estremamente luminosi nei raggi gamma (in altre parole non se ne ha una visione diretta, ma solo ricostruibile dalla luminosità che perviene all’osservatore). Tuttavia, l’urto smorza la velocità e di conseguenza anche la luminosità del getto.

Cosa succede realmente?

Facciamo due ipotesi:

(1) Il getto è perfettamente sferico e quindi dovrebbe mostrarci una semisfera illuminata. Tuttavia, a causa dell’effetto che abbiamo appena imparato, la superficie illuminata continua ad aumentare dato che la velocità decresce e si vede una zona sempre più ampia di superficie sferica. Vi sono, perciò due effetti che giocano in contemporanea: la decrescita continua della luminosità intrinseca (calo di temperatura) ma anche un aumento continuo di superficie illuminata. I due effetti comportano una curva di luce (ossia un decremento della luminosità) non troppo ripida, dato che i due effetti giocano in modo opposto. Alla fine, la sfera è tutta visibile, ma la luminosità ha smesso di essere registrabile (il getto ha esaurito la sua capacità di inviare raggi gamma).

(2) Il getto è simile a un cono con superficie esterna sferica. Tuttavia, esso è sempre tutto visibile fin dall’inizio (è molto collimato). Ne segue che la parte illuminata non aumenta  al decrescere della velocità di espansione: la decrescita è solo dovuta alla diminuzione intrinseca della luminosità. L’andamento decrescente della curva di luce  è nuovamente costante, ma più ripido di quello precedente, in quanto non gioca affatto l’aumento dell’area visibile (si vede tutta fin dall’inizio).

Le due ipotesi, però, potrebbero convivere. Infatti, all’inizio la velocità di espansione è talmente alta che è visibile sono una parte del getto collimato. Al decrescere della velocità, la parte visibile aumenta e quindi siamo nella ipotesi (1): la diminuzione della luminosità non è troppo ripida. A un certo momento, però, tutta la superficie esterna del getto risulta visibile e si innesca il meccanismo (2): la decrescita è più ripida perché dipende solo dalla diminuzione intrinseca della luminosità.

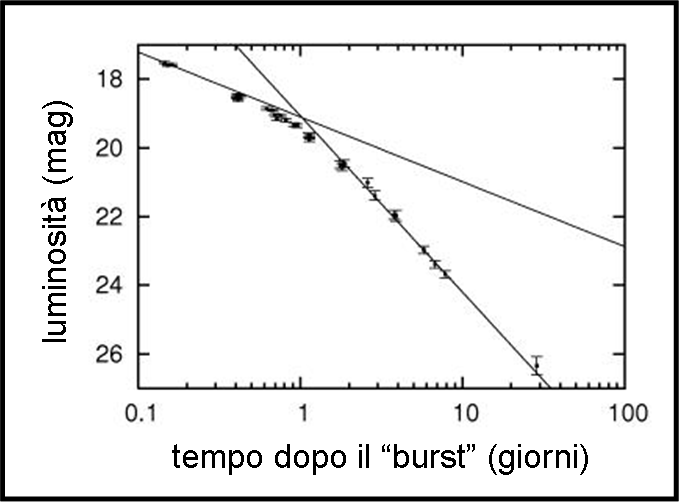
In quest’ultimo caso avremmo la certezza che il getto non è sferico, ma collimato, e avremmo molte informazioni sulla sua velocità e larghezza.  Di seguito mostriamo, come prova REALE e misurabile, la curva di luce di un getto di un buco nero galattico in funzione del tempo, riguardante il lampo gamma GRB 990510 (Fig. 25). L’andamento decrescente subisce un brusco cambiamento di pendenza,  che viene chiamato in gergo “jet break”. La prova di essere di fronte a un getto e non a una bolla sferica e tante altre informazioni di non facile determinazione sono servite. Altro che la sfera-gelato di Pippo e Pappo!

Ritorniamo a bomba: siamo ancora  sicuri che le deformazioni dovute alla limitatezza della velocità della luce, in campo relativistico, siano solo … illusioni e non abbiano risvolti pratici interessantissimi ? Le illusioni, a volte, sono veramente utili per descrivere i fenomeni reali!

Una torta quadrata

Continuiamo il nostro viaggio in balia degli scherzi della luce, attraverso un nuovo quiz che vede interpreti, tanto per cambiare, Pippo e Pappo. La difficoltà è relativa e ormai l’argomento dovrebbe essere ben chiaro a tutti coloro che hanno seguito l'articolo. Questa volta vogliamo anche una semplicissima quantificazione del risultato.

La mamma di Pippo e Pappo ha preparato un altro manicaretto: una torta quadrata sottilissima con quattro tipi di crema. Possiamo considerare praticamente trascurabile il suo spessore, che comunque mostra chiaramente il colore dei vari lati. La posizione di partenza è quella raffigurata nella Fig. 26. Pippo ha una macchina fotografica M di cui AO è l’asse ottico.

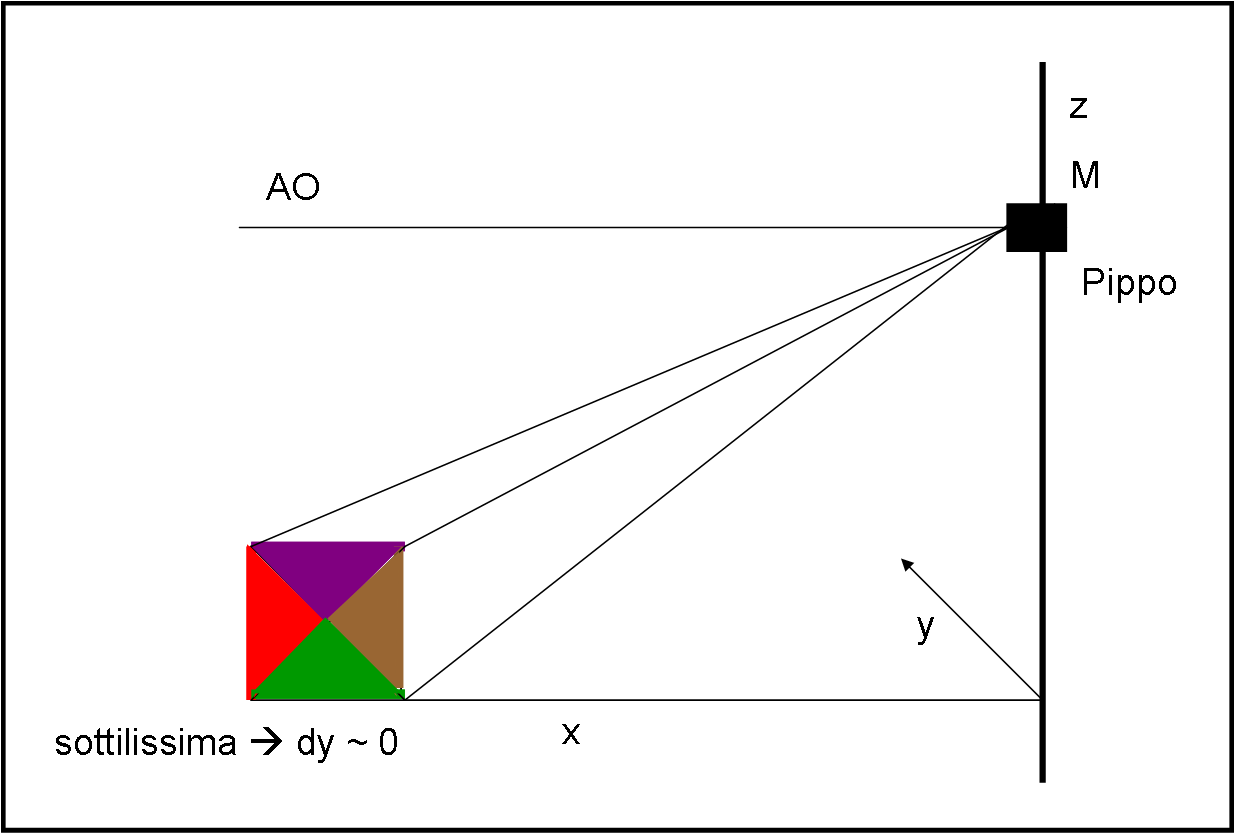
Pappo dice a Pippo di prendere una fotografia della torta ferma. Ovviamente, Pippo può fotografare solo due colori (il marrone della cioccolata e il viola dei mirtilli). Poi Pappo chiede a Pippo: “Cosa devo fare affinché tu riesca a fotografare la crema di fragola (rossa)? Ovviamente, però, non posso ruotare la torta e nemmeno farle superare l’asse z. In poche parole posso solo muoverla lungo l’asse x fino a un certo punto”. Poi aggiunge: “Vorrei che tu mi dicessi cosa deve succedere esattamente, perché capiti ciò che ho detto di riuscire a fare, attraverso una formula matematica semplicissima… Tieni conto, nel caso ce ne fosse bisogno, anche della Relatività Ristretta”.

Come al solito, solo se Pippo saprà dire esattamente cosa deve fare Pappo con la torta, riuscirà a mangiarne la metà.

 

I lettori più “fedeli” e con ottima memoria   avranno riconosciuto in questa domanda la rotazione di Lampa-Penrose-Terrell, che avevamo già trattato, in modo semplificato, in un quiz e in una risposta molto articolata.

In quel caso (QUI) avevamo posto la macchina fotografica a una distanza infinita da un cubo, in modo da avere le traiettorie dei fotoni esattamente perpendicolari alla direzione del moto. Ci eravamo accorti che la contrazione di Lorentz non si riesce a fotografare, a causa della “lentezza” della luce e all’apparizione quasi magica della faccia del cubo che dovrebbe essere invisibile. Avevamo anche notato che questa deformazione corrisponde esattamente a una apparente rotazione del cubo, da cui il nome dell’effetto.

Nel caso di Pippo e Pappo, la faccenda è leggermente più complicata, in quanto abbiamo a che fare con una macchina fotografica posta molto vicina alla torta (quadrata) che si muove a velocità relativistica. Ne segue che l’angolo tra direzione del moto e direzione della macchina fotografica è un parametro fondamentale e guida, in qualche modo, il risultato finale.

La condizione essenziale affinché si riesca a fotografare il lato rosso o il lato marrone dipende dalla componente della velocità della luce lungo la direzione del moto.

In poche parole, se la componente orizzontale (lungo la direzione del moto) della velocità della luce (diretta dal quadrato alla macchina fotografica) è più corta della velocità di spostamento della torta si riesce a vedere il lato rosso (intuitivamente nascosto nella realtà quotidiana). Se invece la componente della luce è maggiore della velocità del quadrato, tutto rientra nella normalità (si fa per dire…) e si vede il lato marrone (già visto da Pippo).

Più semplicemente ancora, data una certa velocità di spostamento, bisogna scegliere la posizione della macchina M o, analogamente, data la posizione della macchina, bisogna scegliere una velocità sufficiente per lo scopo.

Vediamo quanto detto finora, attraverso il semplice schema di Fig. 27.

Nella parte alta si nota cosa capita a un fotone che parta dal lato rosso del quadrato, nell’istante (1). Il quadrato si muove lungo l’asse x più velocemente di quanto non faccia la componente della velocità della luce lungo questa direzione. Il fotone si ritrova, perciò, nell’istante (2) più indietro del lato rosso del quadrato, trascinato verso l’alto dalla componente verticale di c. Il vantaggio del quadrato (d) continua e diventa ancora più grande all’istante (3). Infine, all’istante (4) la via è completamente libera per il fotone che sta per superare, benché in ritardo, la parte superiore del lato rosso del quadrato: non gli resta che dirigersi verso la macchina fotografica M.

Ben diversa è la situazione per il fotone che parte dal lato marrone del quadrato. Lui vorrebbe lanciarsi verso la macchina fotografica, ma il quadrato è più rapido, lungo la direzione x, e, quindi, il fotone non riesce nemmeno a muoversi in quanto viene immediatamente assorbito dal lato del quadrato. Nessun fotone riesce a lasciare il quadrato e il lato marrone non può che risultare invisibile per la macchina fotografica M.

Si ha un risultato decisamente lontano da ciò che capita nelle condizioni “normali” di tutti giorni. Il quadrato vede impresso, sul piano focale, il lato che dovrebbe essere sempre nascosto alla vista. Ricordiamo, infatti, che il quadrato NON può superare la verticale rispetto alla macchina M.

In semplici parole matematiche, possiamo dire che per poter vedere il lato rosso -e non quello marrone- è necessario che valga la relazione:

v > c cosα

dove α è l’angolo formato tra la direzione del moto del quadrato e la direzione della macchina fotografica M.

Per avere la massima sicurezza che questo accada, le condizioni migliori sono quelle in cui l’angolo venga misurato dal limite superiore del lato rosso. Se per lui vale la relazione precedente, essa deve valere sicuramente per tutti quelli inferiori (aumenta l’angolo α e quindi diminuisce ancora di più il coseno e, quindi, la componete orizzontale della velocità della luce).

Non vi è sicuramente bisogno di ripetere la Fig. 27 per il caso in cui la componente di c risulti più grande di v (angolo α più piccolo). In questo caso è ovvio che siano i fotoni del lato rosso che non riescono a lasciarlo, venendo subito assorbiti, mentre quelli marroni scappano immediatamente verso la macchina M. La fotografia assume un aspetto più normale…

Vediamo, allora, come si deforma il nostro quadrato nei due casi, regolati dalla direzione di M.

Cominciano (Fig. 28) con quello che permetterebbe a Pippo di guadagnarsi la torta.

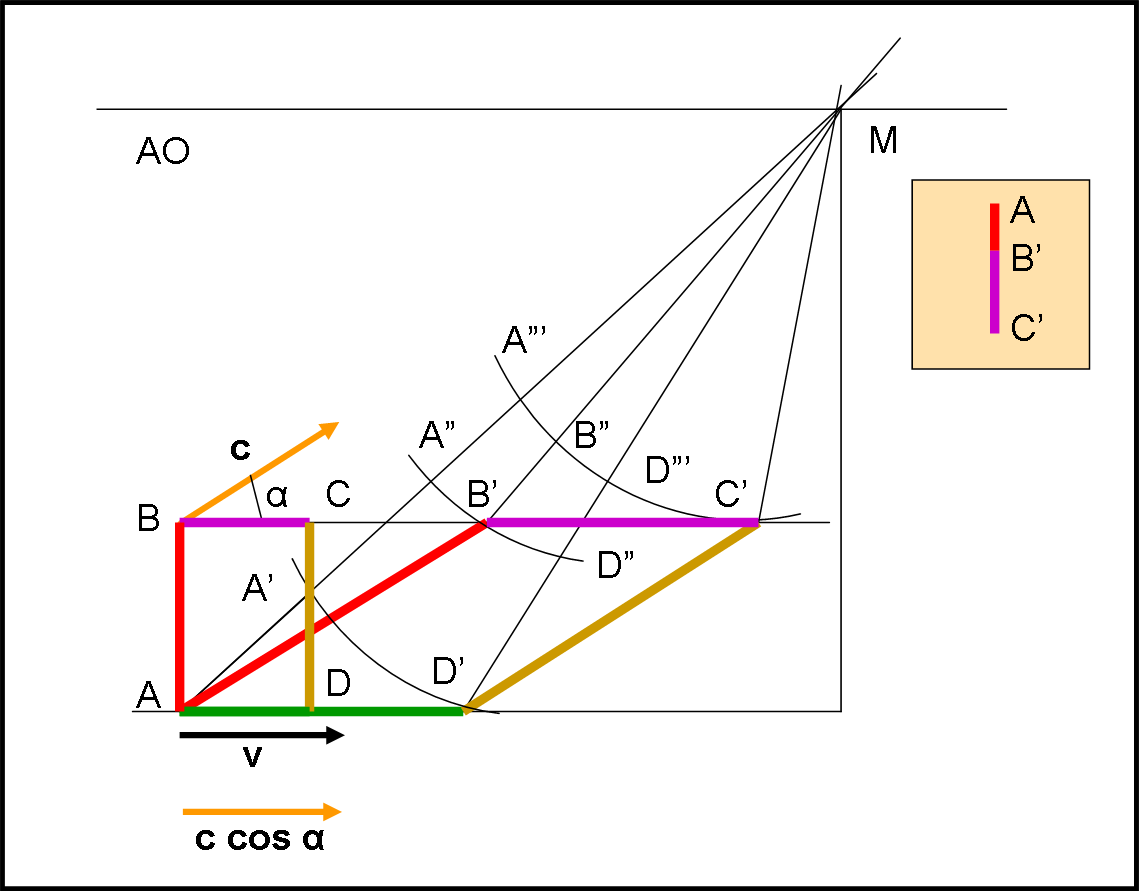
La componente della velocità della luce è minore della velocità con cui si muove il quadrato. Per capire cosa fotograferebbe  M, bisogna far partire i fotoni al momento giusto, considerando anche quelli che non possono arrivare. Ragione per cui immaginiamo, per un momento, il quadrato fatto di vetro, trasparente alla radiazione luminosa. Il quadrato è stato contratto a causa della trasformazione di Lorentz.

Per arrivare al giusto tempo su M, deve partire per primo (in realtà i fotoni partono continuamente, ma noi dobbiamo considerarne uno in particolare) quello più lontano dalla macchina fotografica, ossia quello che corrisponde al vertice A. Lui non ha problemi di vetro trasparente oppure no, come abbiamo visto precedentemente e si lancia senza problemi verso M. Il secondo a partire è quello di D, che teoricamente sarebbe subito assorbito. Ma noi lo facciamo comunque proseguire, eliminandolo a tempo debito. Il momento della sua partenza dipende dal percorso già compiuto dal fotone di A. Lui dà il via a D’, quando si viene a trovare in A’, ossia quando le distanze A’M e D’M sono uguali (solo così arriveranno insieme su M). Non ci stupiamo di certo se il lato contratto AD diventa molto più lungo (A’D’), ricordando quanto descritto riguardo al singolo righello che si muove in modo orizzontale.

Configurazione analoga si ha per il fotone B. Anche lui deve aspettare quello partito da A e quello partito da D. Il momento fatidico per lasciare il quadrato è quando B’ dista da M lo stessa distanza di A” e D”. B’ è spostato in avanti rispetto a B, ricordando come un righello (AB) perpendicolare alla direzione del moto si piega in avanti. In realtà, il segmento dovrebbe essere curvilineo, ma la sua lunghezza è talmente piccola, rispetto al caso del righello perpendicolare, che possiamo considerarlo rettilineo.

Non ci resta adesso che identificare il momento della partenza di C. Basta, calcolare la distanza allungata rispetto a B’ con il solito metodo già richiamato e si localizza C’. A questo punto i quattro fotoni proseguono indisturbati fino a M, dato che devono percorrere una distanza del tutto identica. La foto è fatta e ciò che si vede è rappresentato nell'inserto vicino a M (ricordiamo che invertiamo l'immagine)

Non ci rimane, adesso, che riempire la torta e quindi annullare il fotone che viene assorbito dalla sua “pasta”. Lui è, ovviamente, quello proveniente da D’ e, quindi, i lati invisibili risultano essere AD e DC. Pippo vede il lato rosso, dopo aver visto, prima della partenza, anche quello marrone, oltre a quello viola: tre colori, proprio come gli si chiedeva di fare!

Non voglio nemmeno descrivere cosa succede nel caso che Pippo non capisca cosa deve chiedere di fare a Pappo. Basta abbassare di molto la macchina fotografica M e rendere, perciò, molto più piccolo l’angolo α. Adesso è la luce che viaggia più veloce lungo l’asse x e quindi, come mostra la Fig. 29, non si vede più il lato rosso, ma nuovamente quello marrone.

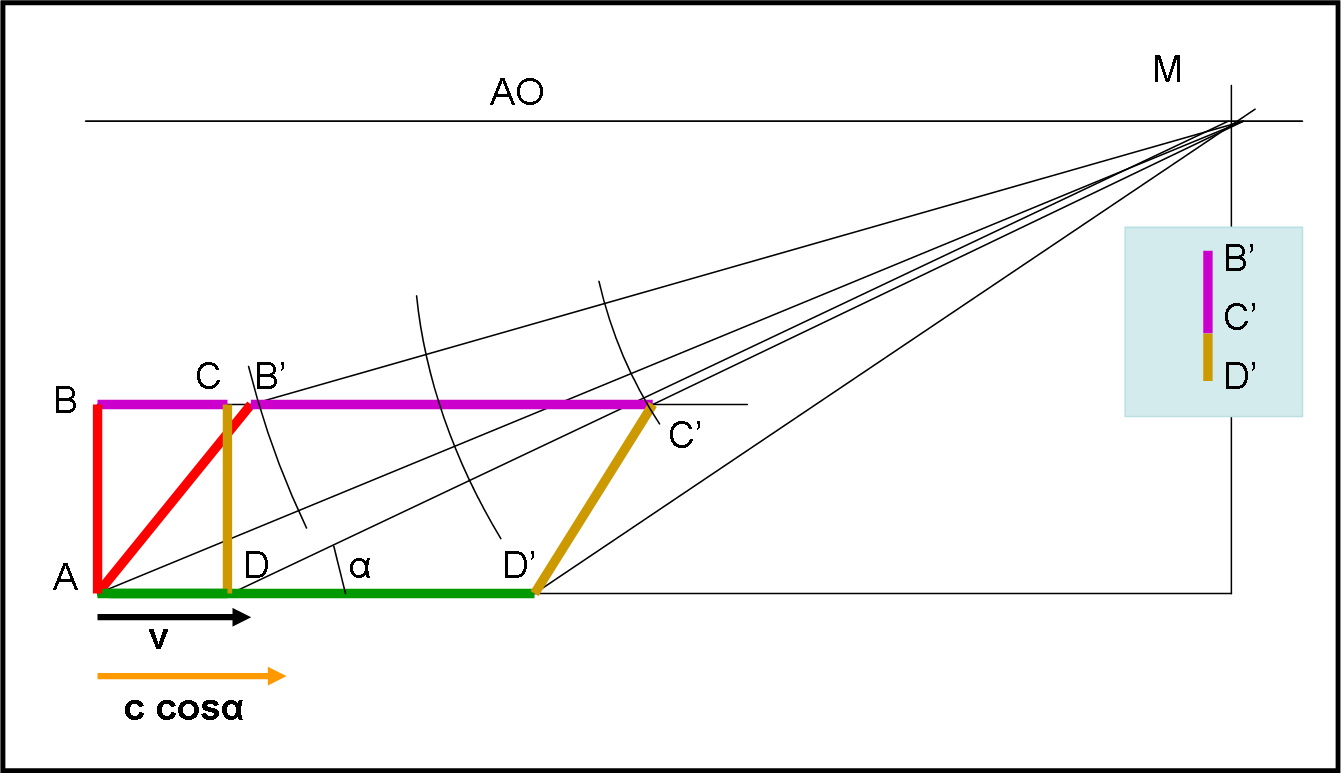
Per questa volta, diamo la vittoria a Pippo (quel Pappo sta diventando troppo saputello…).

 

P.S.: dedicato ai giocatori d’azzardo. Manovrando sapientemente i dadi si possono vincere molti quattrini, senza barare, dato che la velocità relativistica è un tipo di lancio permesso e fa vedere ciò che solitamente non si vede… (è tenuta in conto, ovviamente, anche la prospettiva).

ANIMAZIONE (sotto i dadi fermi, sopra un dado in moto relativistico)

Un monumento inaspettato

Ciò che abbiamo analizzato finora è un problema di tipo puramente visivo, non misurabile se non nel piano focale dell’immagine ripresa da una macchina fotografica. E’ un po’ come fotografare il cielo e vedere due stelle molto vicine, quando in realtà la loro distanza è decisamente più grande.

Finora, abbiamo descritto come un righello in moto relativistico possa allungarsi o possa curvarsi a seconda della sua posizione rispetto alla macchina fotografica. Abbiamo anche visto come non sia per niente difficile osservare ciò che dovrebbe essere nascosto e nascondere ciò che dovrebbe essere visibile. Ne è scaturita, alla fine, la celebre rotazione di Lampa - Penrose – Teller (QUI).  Abbiamo trattato il tutto senza occuparci dell’aberrazione luminosa e dei suoi effetti sia sulla contrazione dell’immagine (e apparente allontanamento di qualcosa che viaggia verso di noi) sia sui "colori", creati dall’effetto doppler.

Lasciamo ancora da parte quest’ultimo effetto e immaginiamo di muoverci a grande velocità lungo le strade di una città tedesca (ciò deriva dalla nazionalità di chi ha preparato l’animazione al computer). Il breve viaggio lo trovate qui di seguito e potete riconoscere tanti effetti ormai ben recepiti: case che si incurvano, pareti che sbucano dalle zone nascoste, un iniziale apparente allontanamento della scena e molto altro. Un bel riassunto di quanto visto finora.

video

Tuttavia, mentre la nostra "macchina" gira come una disperata in un mondo apparentemente assurdo, improvvisamente appare un monumento che sembra del tutto alieno! Che cosa rappresenta e che cosa lo fa apparire così diverso dal pazzo mondo che ci circonda?

Dopo aver dato la (facile) risposta non resta che dimostrare la sua “stranissima” apparenza.

E’ interessante notare che la figura più simmetrica che esista è proprio quella che non subisce deformazioni della propria forma.

Non ha nemmeno senso perdersi in lunghi discorsi. Una sfera viene contratta, se viaggia a grande velocità, diventando un ellissoide schiacciato lungo la direzione del moto. Se non fosse contratta dalla RR, si deformerebbe secondo un ellissoide il cui lato lungo è proprio nel senso del moto. Non è difficile capirlo ripensando a quanto trovato finora. Tuttavia, costruendo ciò che si vedrebbe alla fine, unendo i due effetti (uno reale e uno apparente), si torna alla figura come appare in quiete.

Se, però, inserissimo dei disegni sulla superficie sferica vedremmo, comunque, la rotazione di Lampa - Penrose - Terrell su di essi: quelli nascosti “ruoterebbero” verso di noi fino a mettersi in mostra.

Meglio di tante parole, possono chiarire la situazione delle figure .

Innanzitutto, ecco la visione della piazza e del monumento…

Poi come viene deformata la nostra sfera attraverso la contrazione di Lorentz e la lentezza della luce, separatemente …

Il filmato ci mostra che, alla fine, la sfera rimane una sfera, con i disegni che ruotano…

http://th.physik.uni-frankfurt.de/~scherer/qmd/mpegs/lampa_trick_penrose.mpg

Infine, un bel video che mostra la costruzione di ciò che si vede realmente (eseguita solo su un piano). Chi vuole divertirsi può fare anche di meglio…

http://th.physik.uni-frankfurt.de/~scherer/qmd/mpegs/lampa_trick_penrose.mpg

Cari amici, la relatività ristretta sarà una vera magia, ma la lentezza della luce ne combina proprio di belle!