QUIZ: A carte scoperte (NEW! Inserito filmato)
Dopo l'incredibile vicenda della lotteria, vinta e dilapidata in pochi giorni, il nostro Giovanni ha messo la testa a posto (troppo tardi, direte voi). Ora non gioca più al casinò e neanche alla lotteria. Quando vede i bigliettini dei “gratta e vinci” gli viene l'orticaria.
Recentemente però ha letto nel blog (lo frequenta come lettore ma non ha mai scritto una riga di commento, purtroppo) il bel quiz proposto da Valentina, quello della carta da indovinare in base ad una serie di manipolazioni e conteggi, e gli è proprio piaciuto.
Così, seguendo questa ispirazione, si è inventato un gioco che, invece di utilizzare il classico mazzo da 52 carte, ne impiega solo 21.
Pensate che sia più facile? Vedremo...
Certo, se il mazzo fosse composto paradossalmente da una sola carta sarebbe facilissimo, senza far calcoli indovinarla, ma 21 sono sempre un numero rispettabile.
Insomma, si prendono a casaccio 21 carte delle 52 classiche e si forma questo mazzo.
Poi... ma lasciamolo spiegare da Giovanni al suo amico Amilcare.
“Ecco, Amilcare, qui ci sono 21 carte, ora le dispongo una ad una in questi tre mazzetti e te le faccio pure vedere. Tu scegli, senza dirmi nulla, una delle carte che vedi passare. Bada bene di ricordartela.”
“Va bene, starò attento” risponde pazientemente Amilcare.
“Ecco, ora che i tre mazzetti, di 7 carte ciascuno, sono completati, devi dirmi in quale mazzo si trova la carta che hai scelto... Questo qui? Bene, adesso lo piazzo al centro tra gli altri due: uno sotto, poi quello con la carta da indovinare in mezzo, e infine l'altro sopra. Così ho di nuovo un mazzo di 21 carte.”
Giovanni muove con destrezza le carte, eseguendo le operazioni mentre le descrive, sotto lo sguardo incuriosito di Amilcare.
“Ripetiamo ora la suddivisione in tre mazzi, procedendo in modo ordinato: si dispongono le prime tre carte, dopodiché la 4° carta andrà posizionata sulla 1°, la 5° sulla 2°, la 6° sulla 3°, la 7° sulla 1° (e 4°) e così via. Le carte sono sempre visibili, quindi mi saprai dire in quale mazzo adesso è finita quella che hai scelto. Ricompongo come prima un solo mazzo di 21 carte mettendo al centro il mazzetto con la carta incognita.”
E così fa, con agilità e disinvoltura.
“Infine, per la terza ed ultima volta, ripeto il procedimento...Ecco, vediamo insieme le carte, una dopo l'altra, e ti dico... con certezza... è questa qui !”
“Eh sì, Giovanni, hai proprio indovinato, ma come lo hai capito?”
Amilcare non nasconde la sua meraviglia e aggiunge, un po' scherzando e un po' sul serio. “Con questi trucchetti, se ne inventi altri, puoi avviarti a una carriera di prestigiatore. Così, invece di perdere i soldi con le carte da gioco, puoi trarne profitto, esibendoti in qualche festa di compleanno o in qualche sagra paesana e arrotondare lo stipendio...”
Dice bene Amilcare, ma voi avete capito qual è il trucco?
- Come fa Giovanni ad indovinare la carta scelta da Amilcare?
- Qual è il ragionamento matematico che c'è dietro?
Potete anche rispondere ad una sola di queste domande.
QUI la soluzione
12 commenti
AVVISO AI POTENZIALI SOLUTORI
E' stato inserito nel testo del quiz un filmato che illustra chiaramente come procedere nella formazione dei mazzi.
Cari amici, questo quiz è proprio curioso. Se invece di 21 carte ne usassimo solo tre, avremmo mazzetti molto particolari, tre mazzetti di una sola carta ciascuna....
Ma formalmente anche un insieme che contiene un solo elemento è comunque un insieme.
Allora, mostro i miei tre "mazzetti" all'amico e gli chiedo in quale dei tre si trova la carta che ha scelto. In realtà, indicandomi il mazzetto mi indica proprio quella carta e il gioco è già concluso.
Ma cosa succede se, invece di mazzetti di una sola carta ho a che fare con mazzetti di tre carte ciascuno?
L'indicazione iniziale non basta a darmi la risposta, ma restringe il campo ad un insieme di tre sospettati (le tre carte del mazzetto indicatomi).
A questo punto mi trovo in una situazione analoga al primo caso: basta che le tre carte siano disposte in colonne diverse e il gioco è fatto...
E se le carte di ogni mazzetto fossero 5, oppure 7 (come nel caso del quiz?)
Bene, continuate un po' voi...
Oh, ma stanno tutti a fare e rifare i tre mazzi di carte ?...
Credo che tutti sappiamo che trucco usi il prestigiatore, e non rispondano alla prima domanda perché la considerano banale. Bello sarebbe risolvere la seconda parte
ovvero dare una spiegazione matematica della posizione fissa assunta dalla carta scelta. una piccola domanda - suggerimento aperta a tutti: Dopo il primo giro che posizione occupa nel mazzo da 21 carte la carta scelta?
o
scusate, potrebbe sembrare poco chiaro: Che intervallo di posizioni può occupare la carta scelta?
Dall'8° alla 14°?
SI.
Chiamiamo x tale posizione alla'interno del mazzo da 21.
Quindi 8<=x<=14 all'interno del mazzo da 21 carte.
Adesso prima di pensare al secondo giro di carte, bisogna ricordarsi dell'algoritmo di Euclide della divisione ( x=3*q+r); la posizione p della carta scelta rifacendo i tre mazzetti sarà relativamente al mazzetto da sette in cui finisce compresa fra.. (ricordiamo che il resto può essere 0,1,2)
Propongo questo metodo, ma se ne avete trovato altri ben vengano.
Sappiamo che la carta si trova in questa posizione;8<=x<=14; al secondo giro analizziamo i due casi estremi, cioè x=8 2 x=14
caso 8 (potete verificarlo con le carte se volete)
la carta va a finire ne 2° mazzetto; infatti 8:3 fa 2 con resto di 2,quindi va a finire nel secondo mazzetto in posizione 3; se x=14, 14:3=4 con resto di 2; quindi va finire nel secondo mazzetto in posizione relativa 5
quindi , nel mazzetto da sette occuperà una posizione y compresa fra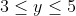
e, mettendo al centro il mazzetto, la carte finirà in una posizione compresa fra 
(devo metterla i mezzo, quindi davanti avrà 7 carte) ovvero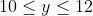 
; Qualcuno mi sa dire dove va a finire la carta al terzo giro?
Cari maghi, dopo averci pensato un po' credo di aver capito che "leq" è una parola magica che significa "less or equal" , cioè minore o uguale, lo dico per quelli che la stanno cercando in wikipedia...
Allora, da quanto ho capito, quando eseguo la divisione del signor Euclide, il risultato mi indica quante sono le righe complete di tre carte che potrò posizionare sul tavolo.
Se il resto della divisione è 0, non ci sono altre carte, quindi la carta incriminata sarà l'ultima della riga indicata dal risultato, che è anche la sua posizione nel mazzetto che la contiene. Il mazzetto in questo caso sarà il terzo.
Ma se il resto è diverso da zero, oltre alle righe complete ne formerò una successiva, incompleta (cioè la posizione della carta sarà data da " valore del risultato + 1) e il mazzetto sarà il primo (resto 1) o il secondo (resto 2).
ma scusate non si vede il segno di minore uguale ? Quella che intendi ê la sintassi latex. Ma io vedo tutto correttamente anche da cellulare
comunque quello che hai detto é giusto
Forza siamo quasi arrivati al dunque
In effetti ora si vede il simbolo matematico, ma per qualche strano incantesimo, per un certo intervallo di tempo, invece del simbolo, appariva il codice corrispondente, con la conseguenza di rendere meno chiaro il tutto.