Per una trattazione completa dell'entrata nel buco nero, si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Questo articolo lo dovevo a un genio come Karl Schwarzschild, anche solo per il fatto di essere stato il primo a trovare una soluzione delle equazioni della relatività generale di Einstein. Inoltre, proprio la sua metrica viene utilizzata per poter descrivere ciò che capita all’interno dell’orizzonte degli eventi e dare il via ai diagrammi di Penrose (che abbiamo già introdotto). Non dimentichiamo, inoltre, che proprio la sua soluzione ha portato alla conoscenza degli attori più esotici del Teatro dell’Universo, i buchi neri. Ho dovuto limitare la descrizione alle parti maggiormente divulgabili, tralasciando le parti più “matematiche” e complesse. Spero che i concetti generali siano comunque facilmente comprensibili. Per i più esperti ho riportato i link a un paio di articoli che mi sembrano veramente completi.

Un breve richiamo

Cominciamo richiamando in modo ultra semplificato alcuni concetti base che abbiamo imparato dalla Relatività Ristretta (RR) e dalla Relatività Generale (RG).

Se non vi sono masse in giro lo spaziotempo può essere considerato piatto ed è perfettamente descritto dalla RR e dal diagramma di Minkowski. Possiamo anche spingerci un po’ oltre e dire che la relatività ristretta si può applicare tranquillamente, se non ci si avvicina troppo ai corpi celesti, soprattutto se molto massicci. In altre parole, essa ci permette di scrivere le equazioni del moto (e non solo) per oggetti che si muovano a velocità costante, senza subire accelerazioni come quella di gravità.

Già con questa semplificazione scopriamo che spazio e tempo non possono separarsi e quello che fa uno dei due influenza senza scampo ciò che fa l’altro. Non solo, però… descrivendo la dinamica si arriva nientedimeno che alla formula più famosa della Fisica, quella che ci dimostra in modo semplice e immediato che massa ed energia sono la stessa cosa. E dico poco…

Una rivoluzione fantastica che permette di studiare fisicamente le azioni delle particelle più piccole, per le quali la velocità della luce non è un meta tanto lontana. Ricordiamo, tra l’altro, che riducendo le velocità relative si ricade senza problemi nella meccanica newtoniana: un punto assolutamente da non trascurare e che dimostra come la RR non distrugga assolutamente la meccanica newtoniana, ma la amplifichi e raffini.

Nello spaziotempo relativistico al posto della distanza delle tre dimensioni nasce un invariante che lega le quattro coordinate e che sembra prendere a calci il teorema di Pitagora quando viene disegnato nel diagramma di Minkowski. Teniamolo bene a mente perché è proprio lui che ci permetterà di descrivere in modo “semplice” la geometria di Karl. Questo invariante diventa la “distanza” tra due eventi (e non due punti) nello spaziotempo a quattro dimensioni.

Fin qui tutto bene… ma cosa capita quando una certa massa fa sentire la sua gravità? Per Einstein il problema si risolve cambiando la geometria dello spaziotempo. Niente di veramente speciale a parole, ma incredibile nella sua genialità e perfezione. Lo spaziotempo si curva, Euclide va a farsi benedire e la semplice legge di Newton (F = ma) diventa leggermente più complicata, nascondendo al suo interno ben 16 equazioni all’apparenza irrisolvibili. Tuttavia, dentro di loro c’è tutto per capire cosa succede in un ambiente in cui la gravità entra in gioco e domina il moto delle particelle. Esse descrivono l’ambiente in cui fa la sua comparsa la materia e permette di stabilire il moto di chi si immerge al suo interno e viceversa.

Riflettiamoci sopra e pensiamo alle onde gravitazionali, ad esempio. Basta tener conto che due masse immense si muovano accelerando secondo traiettorie descritte perfettamente dalle equazioni ed ecco che ne esce fuori una vibrazione dell’intera struttura spaziotemporale. In fondo è estremamente banale, una volta che l’ambiente è stato descritto per qualsiasi configurazione possibile. Banale, generale, preciso e, quindi… geniale!

Semplificando di molto, basterebbe dire che le equazioni di Einstein determinano la geometria dello spaziotempo in funzione della materia che è contenuta al suo interno. Questa geometria permette, infine, di determinare il moto della materia. Cari amici, non potremo mai smettere di stupirci… e chi dice che Einstein ha recuperato “pezzi” a destra e a sinistra, ordinandoli secondo un unico schema, dovrebbe pensare alla Gioconda (o a quello che preferite): essa presenta un volto, un sorriso, uno sfondo paesaggistico, qualche tocco di pennello più o meno accentuato, un mix di colori… cose che tutti potevano conoscere, vedere e toccare. Eppure uno solo è riuscito a rendere la Natura sotto forma di essere umano, una trasformazione che si realizza continuamente sotto gli occhi di chi l’ammira. No, con la relatività, Einstein ha creato un capolavoro artistico e non solo scientifico.

Torniamo a noi…

Ricordate quanto avevamo fatto partendo dalla legge di Newton per arrivare alle leggi di Keplero, determinando le equazioni del moto? Non era stata cosa molto facile (e non parliamo del problema dei tre corpi)… Bene, le equazioni di Einstein permettono di fare la stessa cosa in modo ben più generale e completo, per qualsiasi configurazione geometrica della materia.

Non prendetevela se ribadisco un concetto ormai ben conosciuto, ma che può sempre essere in agguato e creare fraintendimenti e conclusioni errate. Sia nella RR che nella RG siamo sempre in uno spaziotempo a quattro dimensioni. Non facciamoci illudere dal diagramma di Minkowski in cui lo spazio si limita a una sola dimensione. In quel caso, lo spaziotempo è piatto non perché usiamo il piano del foglio, ma perché , la sua geometria e “quasi” euclidea e non risente di curvature. Nella RG lo spaziotempo si curva, ma le sue dimensioni restano sempre quattro.

Pensare di rappresentare con delle figure realistiche queste varie situazioni è impossibile. Abbiamo dovuto e dovremo utilizzare diagrammi “di comodo” che permettano di evidenziare i parametri fondamentali in modo intuitivo, escludendo, però, qualsiasi facile estrapolazione alla realtà effettiva. Abbiamo già fatto vedere (QUI) come la forma a imbuto che spesso descrive graficamente un buco nero porti spesso a interpretazioni e convinzioni completamente errate (e la metrica di Karl va proprio in quella direzione), anche se permette a chi lo comprende appieno di stabilire relazioni perfettamente valide.

Non per niente, il grande Feynman (e io l’ho seguito disciplinatamente) aveva preferito utilizzare una piastra a calore crescente verso l’esterno per definire la curvatura dello spaziotempo e non la solita sfera che mischia la forma di un  oggetto massivo con la deformazione spaziotemporale. Uno spaziotempo curvo è un ambiente in cui non vale la geometria euclidea. La superficie sferica è solo un  esempio a due dimensioni di ciò che deve essere estrapolato alle quattro dimensioni. Non confondiamoci, mi raccomando…

Appena pubblicata la RG, Einstein aveva utilizzato un’approssimazione abbastanza brutale per fornire ai colleghi prove osservative della sua teoria, attraverso, soprattutto, la deflessione della luce. Lui stesso non era molto convinto che si riuscissero veramente a risolvere le sue equazioni, ben sapendo che cosa contenessero: una specie di scrigno di perle con un chiavistello a prova di qualsiasi ladro. E, invece, il primo ladro giunse quasi subito… e il suo nome era proprio Karl Schwarzschild.

Un genio sfortunato

L’inizio della sua vita sembrava portarlo a una carriera prodigiosa. Nato nel 1873 arrivò al dottorato nel 1896, dopo aver già pubblicato due lavori molto importanti a soli 16 anni. Divenuto professore universitario, lavorò con Minkowski e Hilbert e in breve ottenne l’incarico più prestigioso per uno scienziato tedesco di quei tempi: la direzione dell’Osservatorio Astrofisico di Postdam. Nel 1914 scoppiò la guerra e Karl, ebreo, volle dimostrare il suo attaccamento alla Germania e partì per il fronte. Si comportò molto bene, ma il suo contributo alla patria durò ben poco, in quanto nel 1915 contrasse un terribile morbo della pelle che lo costrinse a entrare in un ospedale vicino al fronte russo. Per passare il tempo, Karl si mise a leggere la teoria di Einstein appena uscita e trovò subito una soluzione delle sue equazioni per un caso molto particolare, ma sufficiente per mettere in luce (si fa per dire) i buchi neri! Scrisse subito a Einstein, inviandogli i suoi calcoli e dicendo: “Come vedete la guerra mi ha trattato abbastanza gentilmente, permettendomi di stare lontano dal fuoco diretto e lasciandomi libero di percorrere questo sentiero nella terra delle vostre idee”. Karl morì sei mesi dopo.

Le ipotesi di Karl

 Ciò che Karl ha fatto è facilmente esprimibile: descrivere lo spaziotempo nei dintorni di una stella o, in generale, di una massa non trascurabile, utilizzando le equazioni di Einstein. Per far ciò ha cercato di semplificare al massimo le ipotesi di partenza. In particolare ha assunto che:

1) Nello spaziotempo considerato esiste solo una massa non trascurabile. Un qualcosa che richiama ciò che capita attorno al nostro Sole, dove la presenza di pianeti e di altra materia diventa del tutto insignificante. In altre parole, l’unica gravità che entra in gioco è quella del Sole o di chi per lui. Non esiste altra massa o energia al di fuori di quella della massa centrale. Il sistema considerato è, quindi, considerato vuoto.

2) La massa presente nello spaziotempo è perfettamente sferica. Questa ipotesi significa che se guardassimo una sfera da una certa distanza rispetto al suo centro, la metrica che misura la gravità, rimarrebbe sempre la stessa. In poche parole, lo spaziotempo è sfericamente simmetrico nelle varie direzioni spaziali.

3) Niente cambia nello spaziotempo rispetto al tempo, ossia lo spaziotempo è statico. In particolare, l’oggetto in questione non ruota e non possiede carica.

Tre assunzioni che non sono così pesanti come potrebbe sembrare a prima vista, ma che comportano semplificazioni enormi nelle equazioni di Einstein. Le 16 equazioni si riducono a una sola, la cui soluzione è esatta.

Sotto queste ipotesi, lo spaziotempo diventa completamente piatto a una certa distanza dalla massa. Più esattamente, esso tende a divenire piatto asintoticamente.

Riassumendo:

Karl intende esaminare e descrivere la geometria di uno spaziotempo all’interno e all’esterno di un corpo sferico che non si muove, non possiede carica, non ruota e non è assolutamente influenzato da azioni esterne. Uno scenario del tutto ideale. La stessa particella che si muove in questo contesto comporta una minima ma sicura influenza. Tuttavia, il modello permette di approssimare in modo quasi perfetto molti oggetti dell’Universo reale, a partire dai singoli pianeti, passando per le stelle e finendo con oggetti del tutto esotici. Notiamo, infatti, che nessuna ipotesi viene fatta riguardo alla composizione del corpo centrale. Stelle di neutroni e buchi neri non sono perciò esclusi da questa trattazione.

La descrizione dello spaziotempo può essere diviso in due parti: quella esterna al corpo sferico e quella interna al corpo sferico. Il volume realmente occupato dal corpo celeste acquista, però, un significato diverso dal solito, dato che la massa viene misurata in … metri, come vedremo tra poco.

Le coordinate

Il primo passo da compiere è utilizzare un sistema di coordinate spaziali diverso da quello cartesiano (x,y,z) comunemente usato. Molto meglio, infatti, affidarsi alle coordinate polari, data la simmetria sferica. Il sistema di coordinate spaziali (a un certo tempo t) è quello rappresentato in Fig. 1.

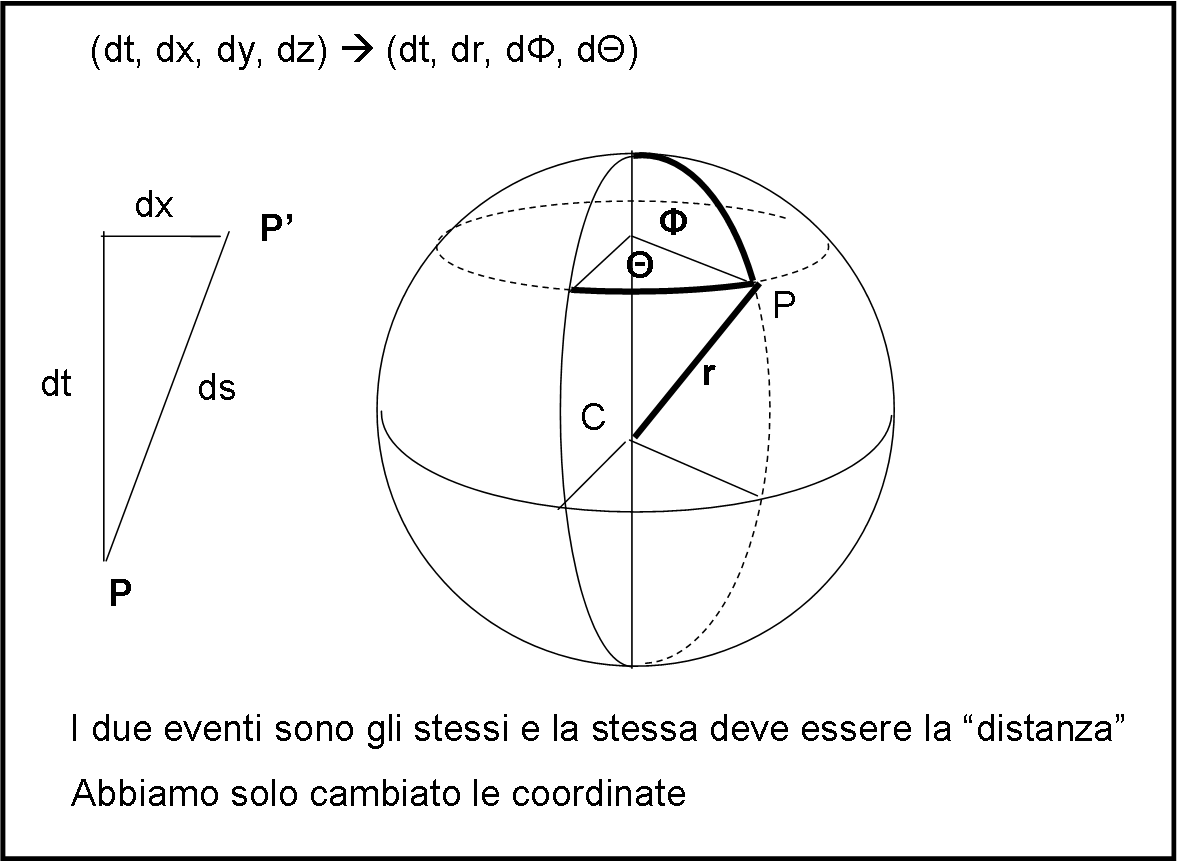
Recuperiamo dalla nostra memoria l’invariate a quattro dimensioni della RR (non dimentichiamoci il tempo, mi raccomando!) e scriviamolo nelle coordinate x,y,z,t:

ds² = dt² – dx² – dy² – dz²

Esso indica la “distanza” spaziotemporale tra due eventi e vale per qualsiasi sistema di riferimento, proprio come la distanza euclidea rimane se stessa pur cambiando sistema di coordinate. Sulla base della Fig. 1, l’invariante prende la forma:

ds² = dt² – dr² – r² dΦ² – r²sin²Φ dΘ²

che possiamo anche scrivere:

ds² = dt² – dr² – r² (dΦ² + sin²Φ dΘ²) = dt² – dr² – r² d²Ω        …. (1)

Notiamo che il differenziale d²Ω non è altro che l’elemento di superficie di una sfera unitaria, per cui non dipende dal raggio. Sarà un fatto molto importante tra poco.

La formula appena scritta descrive l’invariante in uno spazio “vuoto, privo di masse. Ne segue che, dopo aver descritto la geometria di Karl (valida nella RG) dovremmo trovare, per distanze molto alte rispetto al centro del corpo celeste sferico, che l’equazione di Einstein si riduce alla (1).

Costruiamo, adesso, una massa molto speciale, cambiando le sue unità di misura. Facciamo un qualcosa di simile a quanto utilizzato nella RR maneggiando il tempo. Ricordiamo che l’avevamo moltiplicato per c (costante) e avevamo costruito un  tempo che veniva misurato come una distanza spaziale. Infatti:

T = t·c => s·m/s = metri

In altre parole, il tempo veniva misurato in metri e diventava una coordinata non diversa dalle altre tre.

Adesso facciamo qualcosa di simile per la massa del corpo celeste. Moltiplichiamola per G (costante di gravità universale) e dividiamola per c². Si ottiene:

M = m G /c² => (kg) (m³/kg s²) (s²/m²) = metri

Piccolo miracolo… e abbiamo ottenuto una massa misurata in metri.

Vi faccio subito divertire. Quanto vale nel caso del Sole? Essa diventa 1.5 km. Voglio solo ricordarvi, tanto per farvi riflettere un breve attimo, che il celebre raggio di Karl (orizzonte degli eventi) per il Sole risulta essere di 3 km. Proprio il doppio della sua massa espressa in metri… Un caso? Nemmeno per sogno. Abbiate pazienza e lo scopriremo…

La geometria

A questo punto non ci resta che immaginare il nostro Karl, malato nel suo letto di ospedale, che comincia a imporre le sue ipotesi restrittive alle 16 equazioni di Einstein. Uno dopo l’altro i vari tensori vanno a zero o giù di lì e ciò che resta ha la seguente forma (espressa nelle coordinate e nelle unità di misura appena introdotte):

ds² = dt²(1 – 2M/r) – dr²(1 – 2M/r)^-1 - r² d²Ω     ….(2)

Prima di proseguire, vediamo subito cosa succede se r tende a infinito (ci portiamo molto lontani dalla massa centrale). 2M/r tende a zero, per cui la (2) diventa esattamente la (1), la distanza invariante nello spaziotempo piatto! Proprio quello che volevamo…

Riflettiamo sulla (1)

Se poniamo t e r costanti (dt e dr vanno a zero), otteniamo la rappresentazione di una superficie sferica “normale”. Al variare di r le sfere sono una interna all’altra come una specie di matrioska. Lo spaziotempo di Karl è quindi descritto lavorando su sfere di raggio decrescente e poco importa quale sia il vero volume del corpo celeste sferico iniziale, dato che compare solo una massa misurata in metri. Possiamo perciò arrivare tranquillamente fino al valore “limite” di M, che rappresenta la massa del corpo celeste nelle nuove unità di misura. Possiamo, quindi, dire che giungiamo tranquillamente fino alla parte esterna del corpo la cui massa è espressa in metri come il suo raggio.

Attenzione, però, a non commettere un errore madornale. Questa serie di sfere “normali” appaiono tali solo per un osservatore posto molto lontano da loro, ma non certo per chi si muove su di esse. Il righello e l’orologio di quest’ultimo subiscono variazioni sempre più grandi mano a mano che si avvicinano a M (misurata in metri).

Fissiamo, ad esempio, tutte le coordinate e facciamo variare solo il raggio r (tutte le altre differenze vanno a zero). Quello che si ottiene è una sezione dello spazio:

dσ² = – dr²(1 – 2M/r)^-1    …. (3)

L’ho chiamata dσ dato che è una distanza puramente spaziale.

Il diagramma embedding

Se noi diminuiamo la coordinata r in modo costante tra due sfere adiacenti, otteniamo un dσ che aumenta sempre di più, . In altre parole, più vicini andiamo al valore M e più le sfere concentriche si allontanano tra di loro. Tutto ciò può essere rappresentato in Fig. 2, che ci fa subito ricordare il celebre imbuto dei buchi neri (in fondo è la stessa cosa).

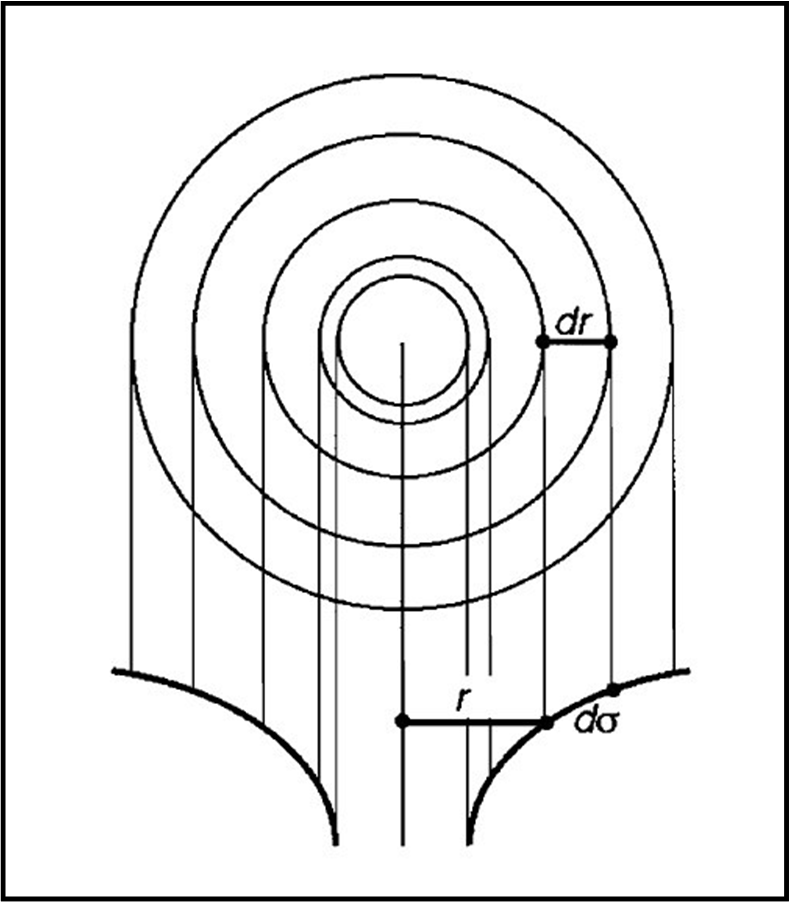
In realtà, tutto si basa sul fatto che misurare un raggio dividendo la circonferenza equatoriale per 2π non è la stessa cosa che misurare il raggio stando sulla superficie sferica (QUI e QUI).

Descriviamo la faccenda in maniera più realistica. Immaginiamo di essere molto distanti dalle sfere concentriche e fissiamoci sui loro cerchi equatoriali. Essi ci appariranno perfettamente equidistanti tra loro per separazioni costanti del raggio. In altre parole, ogni raggio è legato alla circonferenza equatoriale dalla formula 2πr o -se preferiamo- alla superficie sferica dalla relazione 4πr². Da lontano, la metrica di Karl sembra un gioco da bambini… Tuttavia, la situazione è ben diversa per chi misura le distanze PROPRIE (fisiche), viaggiando tra le sfere. La relazione tra le distanze dr misurate tra due sfere da un osservatore all’infinito e quelle dσ misurate localmente per le stesse due sfere è data proprio dalla (3).

In modo più generale (tenendo conto anche del tempo), si deve ricordare che tutte le misure di spazio e tempo sono puramente locali, ossia dipendono dal righello e dall’orologio di chi appartiene a uno spaziotempo curvo. Le coordinate di partenza (all’infinito) e quelle locali (proprie) sono legate in modo non banale dalla metrica di Karl, in uno spaziotempo curvo. Tutto ciò può essere raffigurato in un diagramma a tre dimensioni proiettato su due dimensioni, con i limiti concettuali (tutto è, fuorché una rappresentazione realistica) che ormai dovremmo conoscere molto bene. Si ottiene il diagramma detto embedding (incastrante o qualcosa del genere) dello spaziotempo di Schwarzschild, rappresentato in Fig. 3. In parole più semplici questo tipo di diagramma è a due dimensioni, ma è visualizzato (embedded) in uno spazio euclideo a tre dimensioni per rendere evidente la sua curvatura.

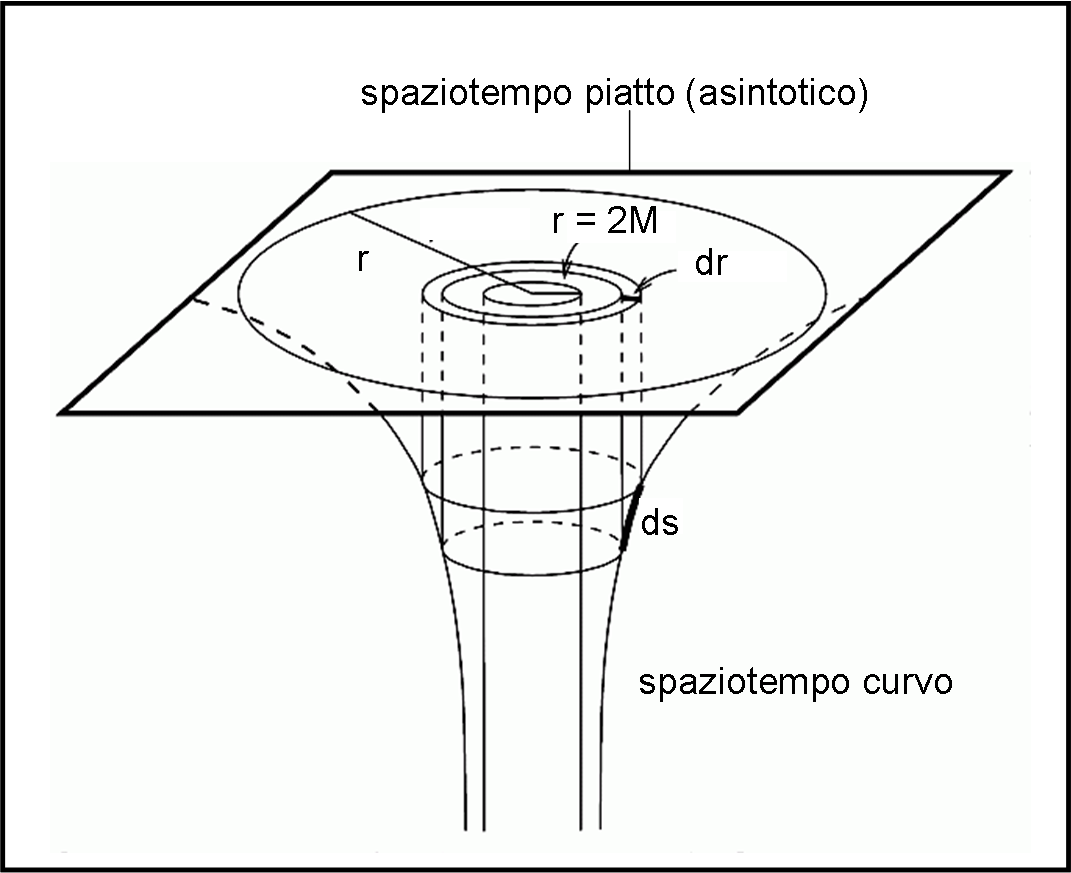
Analizzato lo spazio, pensiamo ora al tempo. Ciò che succede è abbastanza intuitivo… il tempo proprio locale è più piccolo del tempo misurato da lontano, dato che il fattore di curvatura è più piccolo di uno. Il che implica che la frequenza del segnale luminoso emesso da un certo evento risulti più piccola per un osservatore lontano. In poche parole, l’osservatore lontano vede una lunghezza d’onda maggiore, ossia subisce il redshift gravitazionale.

Avvicinandosi al valore limite di r (2M, ci torneremo sopra tra poco), il tempo proprio diventa sempre più piccolo rispetto a quello di un orologio lontano. Per quest’ultimo un singolo tic-tac dell’orologio locale tende a coprire un tempo infinito. Un segnale, perciò, mandato quando r = 2M, impiega un tempo infinito per raggiungere l’osservatore non immerso nello spaziotempo curvo. La sfera che corrisponde a questo valore di r è chiamata ORIZZONTE DEGLI EVENTI. Beh… l’abbiamo ritrovata, lavorando in modo “serio” con la metrica di quel genio di Karl.

Come piccolo (già noto) esercizio, vediamo come la “strana” massa M, possa anche ricavarsi facilmente senza entrare nella metrica di Karl, limitandosi alla velocità di fuga. Notiamo, però, che la vera definizione è data da Karl, ma che il risultato può essere trovato in modo semplificato (a posteriori).

Consideriamo il raggio di un corpo di massa M (normale) per il quale la velocità di fuga sia pari a c. Il problema si può risolvere attraverso l’energia cinetica e potenziale del corpo in questione.

E_c = ½ mv² = ½ mc²

E_P = h g m = h m GM/r²

Ma h = r, per cui:

E_P = mGM/r

Uguagliando le due energie:

½ mc² = mGM/r

r = 2GM/c²

Bene, abbiamo dimostrato che il raggio non è altro che la massa “modificata” moltiplicata per 2. Proprio quello che abbiamo trattato attraverso la metrica di Karl.

Non è difficile, inoltre, determinare la dilatazione del tempo attraverso la (2). Immaginiamo di essere fermi in un punto dello spaziotempo di Karl. In un piccolo intervallo attorno a noi possiamo considerarci nello spazio di Minkowski. Varrebbe quindi un invariante “classico” del tipo:

ds² = dt’² – dx² – dy² – dz²

dove t’ misura il nostro tempo proprio. Essendo fermi, deve valere dx = dy = dz = 0. In quel punto, però, l’invariante deve sempre essere lo stesso, sia per Karl che per Minkowski, per cui risulta (dalla (2)):

dt’² =  dt² (1 – 2M/r)

Ossia:

dt’ = dt (1 – 2M/r)^1/2

Notiamo come, pur essendo ormai in balia di uno spaziotempo dominato della RG, si possa studiare localmente la situazione, approssimandolo con uno spaziotempo di Minkowski. Chi ancora giudicasse la RR una teoria “secondaria” e non realistica sarebbe bene che rivedesse il proprio pensiero. In fondo il diagramma embedding è una serie di tanti piccoli tasselli “piatti” in cui valgono le leggi della RR (vedi Fig. 4).

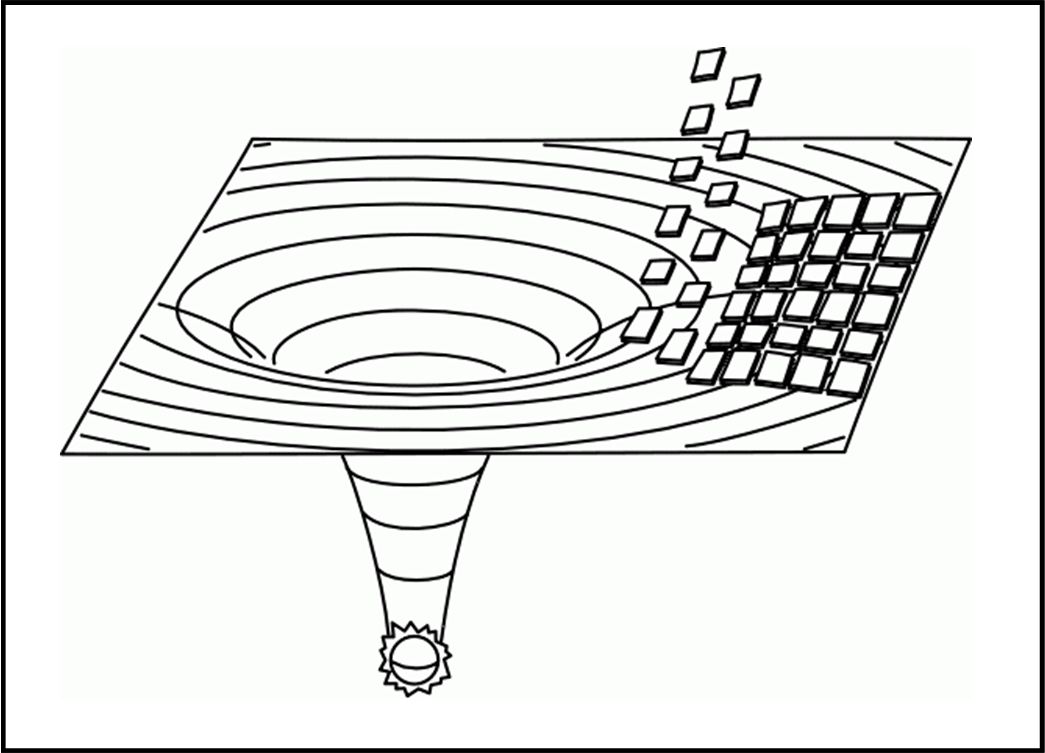
L’orizzonte

Che il raggio r = 2M sia molto particolare si può subito dedurre dalla (2). Per tale valore la parentesi che moltiplica dr² va ad infinito e anche ds². Siamo di fronte a un punto singolare, quello che corrisponde al raggio di Karl o all’orizzonte degli eventi. Un  punto singolare che, però, dà un fastidio abbastanza relativo. Basta infatti cambiare sistema di coordinate per renderlo “inoffensivo”.

Un altro valore per cui ds² va ad infinito è r = 0. Per lui, purtroppo, non si può fare niente: siamo di fronte a una vera singolarità.

La singolarità che si ottiene all’orizzonte è dovuta alla scelta delle coordinate ed è tale solo per chi osserva da lontano e non per chi si trova veramente sulla sfera corrispondente. Ciò che realmente capita (e l’abbiamo già detto varie volte) è una trasformazione delle linee di tipo spazio in linee di tipo tempo. Diciamo meglio: al di fuori dell’orizzonte le linee radiali della geometria di Karl rappresentano intervalli spaziali. Al suo interno, invece, gli intervalli radiali diventano intervalli temporali. Lo stesso Einstein era rimasto molto imbarazzato dal limite dato dall’orizzonte e l’aveva considerato una vera barriera. In realtà, gli intervalli radiali di tipo tempo, all’interno dell’orizzonte, vogliono solo significare, concettualmente, che lo spazio cade verso la singolarità vera, con una velocità superiore a quella della luce. In altre parole, per rimanere spazialmente fermi dentro all’orizzonte bisognerebbe spostarsi a velocità maggiori della luce, il che è impossibile.   Siamo letteralmente trascinati lungo una linea temporale che porta inesorabilmente verso il punto in cui r = 0. Dobbiamo notare che questo cambiamento di linee (da tipo spazio a tipo tempo) è anch’esso legato alle coordinate utilizzate. Ad esempio, utilizzando quelle di Kruskal–Szekeres non vi sarebbe nessun passaggio da spazio a tempo… ma, la sua trattazione la lascio a chi vuole andare veramente per il sottile.

Il diagramma “embedding” completo è quello rappresentato dalla Fig. 5.

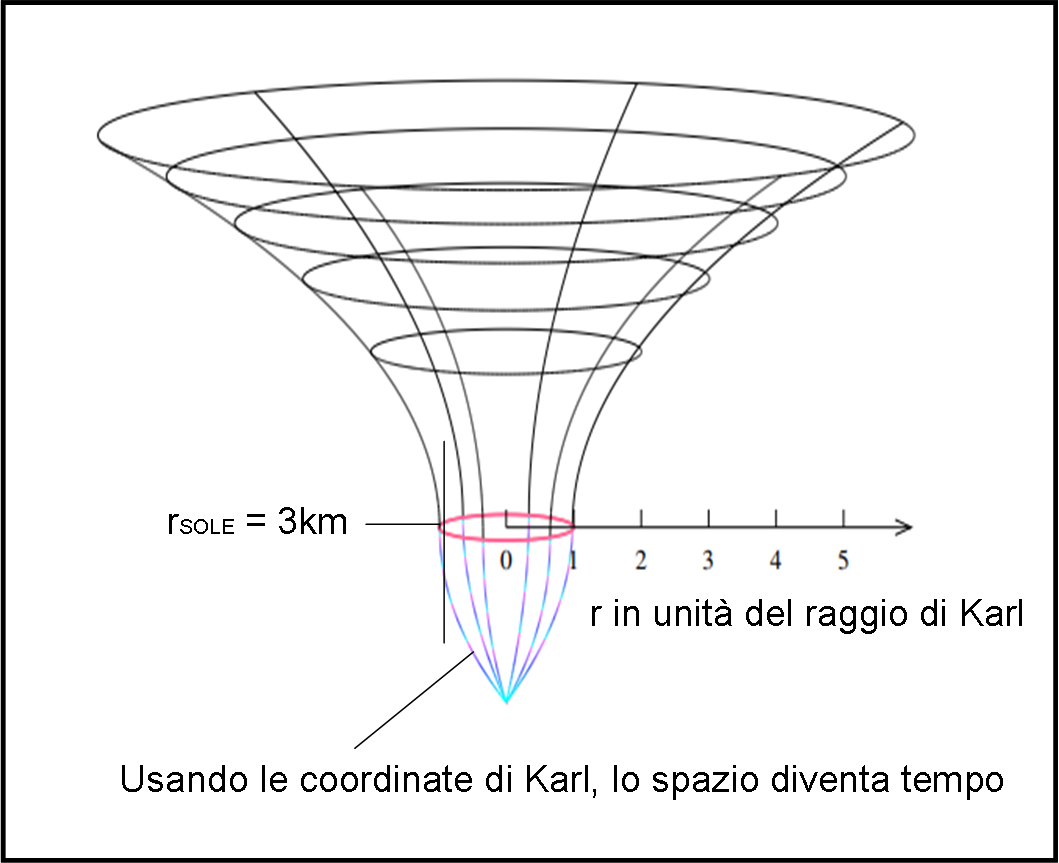
Ciò è vero anche per una stella qualsiasi e non solo per un buco nero (che deve avere la massa reale contenuta all’interno dell’orizzonte). Ricordiamo, infatti, che la massa del Sole, definita in metri, è pari a 1.5 km. Per r = 2M = 3 km, si entra effettivamente all’interno dell’orizzonte degli eventi del Sole e vale l’ultima parte del diagramma di Fig. 5. Tuttavia, il Sole sarebbe un buco nero solo se la sua vera massa fosse contenuta entro i 3 km di raggio.

Descrivere il cambiamento di coordinate per potere trattare la parte più “segreta” del diagramma non è cosa per noi, così come la derivazione della (2), e dobbiamo accettarle come un dato di fatto. Per chi volesse andare oltre, consiglio questo lavoro professionale, ma, nella rete, ve ne sono molti altri (in inglese) e qualcuno anche in italiano

Spero ardentemente che questa trattazione, giocoforza incompleta e semplificata, sia sufficiente a far capire lo splendido lavoro di Karl e quale enorme contributo abbia dato allo sviluppo della RG e alla sua comprensione, ancora non certo conclusasi.  Quanti Nobel avrebbe dovuto portare con sé questa stupefacente teoria, continuamente confermata, malgrado i mille e uno tentativi per trovarne delle crepe. Adesso, possiamo tornare, con maggiore tranquillità, al diagramma completo di Penrose e chissà che non si riesca a cambiare … Universo!

 

In attesa di essere riuniti in un unico approfondimento, QUI trovate tutti gli articoli della serie "Apriamo la porta del buco nero" finora pubblicati