Questo articolo è stato inserito nell'approfondimento dedicato ai Buchi Neri, che raccoglie in modo organico gli articoli più significativi sull'argomento.

 

Questo lungo articolo contiene quelli relativi all'entrata dentro un buco nero, descritto attraverso la metrica di Schwarzschild. Alcune parti contengono concetti e visualizzazioni non banali, anche se sono state escluse tutte le formule matematiche. I risultati, però, sono talmente brillanti, che meritano un piccolo sforzo in più.

Dopo un viaggio verso un buco nero, siamo arrivati al bordo dell’orizzonte degli eventi, ma non siamo entrati veramente nelle “fauci del mostro”. E' venuta l'ora di bussare a quella porta che lascia entrare, ma non uscire...

Ciò che si “vede” all’interno dell’orizzonte degli eventi (ma si riesce a vedere qualcosa?), non può essere descritto attraverso gli effetti a cui siamo abituati quotidianamente e che -pur se con difficoltà- possiamo ancora usare per altri fenomeni celesti di immane energia. L’interno di un buco nero è un altro Universo, dove spazio e tempo perdono il significato che conosciamo normalmente. Dovremmo cambiare i nostri occhi e tutte le sensazioni per descrivere la fenomenologia che avviene.

Potremmo dire che la forza di marea causa la “spaghettificazione” delle cose, allungando la materia in una sola direzione, quella che termina inesorabilmente nella singolarità finale (QUI abbiamo parlato della "spaghettificazione" del campo magnetico generato da un buco nero galattico). Oppure che è necessario un terzo occhio per vedere. O ancora che la curvatura dello spazio-tempo diventa infinita. E che dire dello sdoppiamento dell’orizzonte? Parole di effetto, ma con poco riscontro razionale.

Molto meglio prendere il “toro per le corna” e descrivere cosa sia in realtà un buco nero nell’insieme generale dello spaziotempo, rappresentandolo graficamente in un diagramma bidimensionale, perfettamente logico e preciso, in cui un concetto aleatorio e intangibile come l’infinito sia “facilmente” e concretamente rappresentabile.

Prima di iniziare, dobbiamo fare un’ipotesi importante. Ciò che andremo a trattare si riferisce al caso puramente teorico del buco nero statico di Schwarzschild. Esso non ha rotazione e nemmeno carica elettrica.

I buchi neri stellari nascono due volte…

La prima volta, da tempo immemorabile, attraverso il collasso gravitazionale di una stella dell’Universo molto più massiccia del Sole. O magari esistono da sempre...

La seconda volta quando, poche settimane dopo la pubblicazione della Teoria della Relatività Generale di Einstein, Schwarzschild introduce la sua geometria capace di descrivere lo spazio vuoto che circonda una massa sferica. Pur se relativamente limitata, essa si basa, ovviamente, sulla soluzione delle equazioni di Einstein e la sua applicazione a masse diverse ha messo in luce un raggio critico al di sotto della quale nessuna informazione può più uscire.

Al suo interno, le curve tipo spazio dello spaziotempo di Minkowski diventano linee tipo tempo e qualsiasi linea di Universo è costretta a terminare nella singolarità centrale. Questo raggio prende il nome di raggio di Schwarzschild e se una massa è contenuta completamente all’interno di essa, prende il nome di buco nero, per ovvie ragioni ormai note a tutti. A titolo di esempio, per una massa pari a 30 masse solari, il raggio di Schwarzschild non supera i 100 km.

E’ solo per una curiosa e fortunata coincidenza che questo raggio sia già stato derivato nel 1783, da John Michell, nell’ambito della teoria newtoniana e della natura corpuscolare della luce. In quel caso il raggio critico è quello che deriva dalla velocità di fuga posta uguale a quella della luce, per un corpo di massa M e di raggio r.

Come ormai sappiamo bene (QUI e QUI) nel caso newtoniano è comunque possibile uscire “gentilmente” da tale oggetto celeste, mentre nel caso relativistico non vi è alcuna possibilità.

La geometria di Schwarzschild è illustrata abbastanza bene da un diagramma a due dimensioni che  rappresenta una geometria spaziale a tre dimensioni in un particolare istante t. Esso nasce praticamente attraverso una specie di “matrioska” sferica (ogni sfera è contenuta in un’altra con lo stesso centro, Fig. 1). Si inseriscono particolari coordinate (ne parleremo più avanti) che portano a uno sviluppo su un piano.

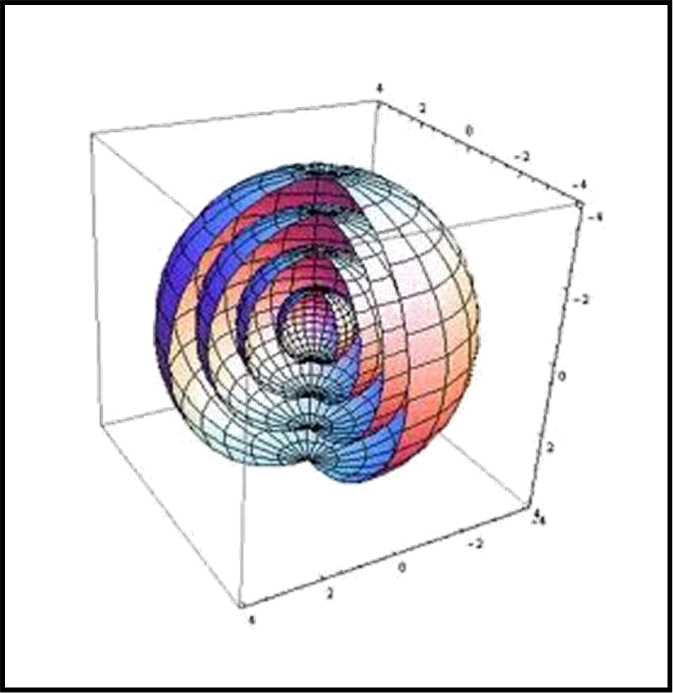
Il suo aspetto finale ricorda molto quello che avevamo criticato come fuorviante nell’ambito della comune descrizione dei buchi neri, simili a imbuti in cui cade la materia (QUI). Una cosa è però “credere” che lo spazio sia un tessuto bidimensionale che si piega e un’altra è una rappresentazione matematica e geometrica che descriva le caratteristiche dello spazio tempo attorno una massa sferica. Purtroppo la metrica di Schwarzschild è un po’  ardua  e dobbiamo limitarne la descrizione ai concetti più importanti. Per chi volesse "saltarla" ne diamo una rappresentazione di massima, senza entrare nei particolari, nella Fig. 2. Alcune considerazioni vanno, comunque, fatte.

Anche solo partendo dalle sue conclusioni è possibile saper leggere molto meglio cosa può capitare all’interno del raggio di Schwarzschild, ossia del celeberrimo orizzonte degli eventi. Non è difficile capire che una di queste sfere ha delle caratteristiche peculiari ed è proprio quella che individua il raggio di Schwarzschild.

Per arrivare al nocciolo della questione è meglio ripetere ancora una volta la storia fisica che porta ai buchi neri. Essa sarà di grande aiuto per capire, secondo Einstein e, di conseguenza, Schwarzschild, il vero significato di “singolarità”.

Ciò che la metrica descrive, la Natura esegue (o viceversa …)

Ciò che succede in Natura è che un corpo può mantenere la propria massa, diminuendo il suo raggio (QUI abbiamo ipotizzato cosa accadrebbe all'orbita della Terra se il Sole riducesse il suo raggio fino a diventare un buco nero... la risposta potrebbe sorprendervi!). Questo fatto porta a limiti che non possono essere previsti e descritta dalla fisica newtoniana, ma solo da quella relativistica. Le leggi di gravità che governano l’interno di un corpo estremamente denso sono completamente impensabili per Newton (la trattazione della gravità newtoniana la trovate QUI).

Prima di arrivare al limite estremo, si trovano alcune situazioni intermedie “di sosta”, dove la materia trova uno stato di equilibrio con la pressione esercitata dal collasso gravitazionale. Queste soste intermedie vengono chiamate stati di degenerazione.

Allo stato iniziale la materia è composta da atomi e la prima barriera è quella in cui la pressione viene bilanciata dalle interazioni elettromagnetiche tra atomi, dettata dalla meccanica quantistica. Questi oggetti prendono il nome di nane bianche e rimangono tali fino al ben noto limite di Chandrasekhar.

Superato questo limite (disinteressandosi degli effetti esplosivi della supernova), l’elettromagnetismo non riesce più a opporsi alla pressione. Gli atomi vengono distrutti e la materia normale viene trasformata in qualcosa che può essere chiamata neutronio. In modo molto semplicistico, si ha la produzione di neutroni dalla combinazione di protoni ed elettroni. La materia cambia stato e riesce a riprendere il comando delle operazioni. Siamo nel secondo momento di sosta  e gli oggetti pendono il nome di stelle di neutroni. Ricordiamo che questa fasi sono già state trattate introducendo direttamente la meccanica quantistica e il principio di esclusione Pauli. Adesso, vogliamo solo ricordarle per vedere i vari oggetti che incontra la metrica di Schwarzschild.

La materia, comunque, continua a collassare, diminuendo il raggio della sfera e mantenendo costante la massa. Ed ecco che si ipotizza uno stato di degenerazione del tutto teorico (per adesso). Esso coincide con il limite di  Tolmann-Oppenheimer-Volkoff. Superano questo limite la materia si trasforma in un gas composto da quark e gluoni. Siamo di fronte alle ipotetiche stelle di quark, mai osservate finora.

Va ricordato, ovviamente, che i vari limiti possono essere raggiunti a seconda della massa iniziale. Non tutte le stelle, ad esempio, possono diventare stelle di neutroni.

Niente ci vieta di superare anche questo limite e di aumentare la pressione. A questo punto non esiste nessun meccanismo, nemmeno teorico, che può riuscire a fermare il collasso della materia. Nemmeno la meccanica quantistica riesce, per adesso, a dare il suo contributo. Il corpo continua ormai liberamente il suo collasso fino a che tutta la materia viene contenuta in una regione di spazio infinitesima. Siamo giunti alla singolarità gravitazionale. A questo punto tutte le coordinate di Schwarzschild divergono e le linee geodetiche di Universo sono obbligate a fermarsi.

Siamo giunti al fondo dell’imbuto e non si è più in grado di descrivere i fenomeni che capitano. Singolarità vuol proprio dire incapacità di descrivere la situazione attraverso qualsiasi legge fisica conosciuta. Tuttavia, quando si entra in questo stadio, il raggio di Schwarzschild è ormai “esposto”, ossia è esterno alla materia che cade verso la singolarità. Come già detto precedentemente, qualsiasi cosa vi sia all’interno di esso prende il nome di buco nero, anche se, fisicamente, esso dovrebbe essere limitato alla singolarità.

Ricordiamo, ancora una volta, che qualsiasi massa sferica ha un suo raggio di Schwarzschild, ma diventa buco nero solo e soltanto quando la materia è tutta compresa dentro di esso.

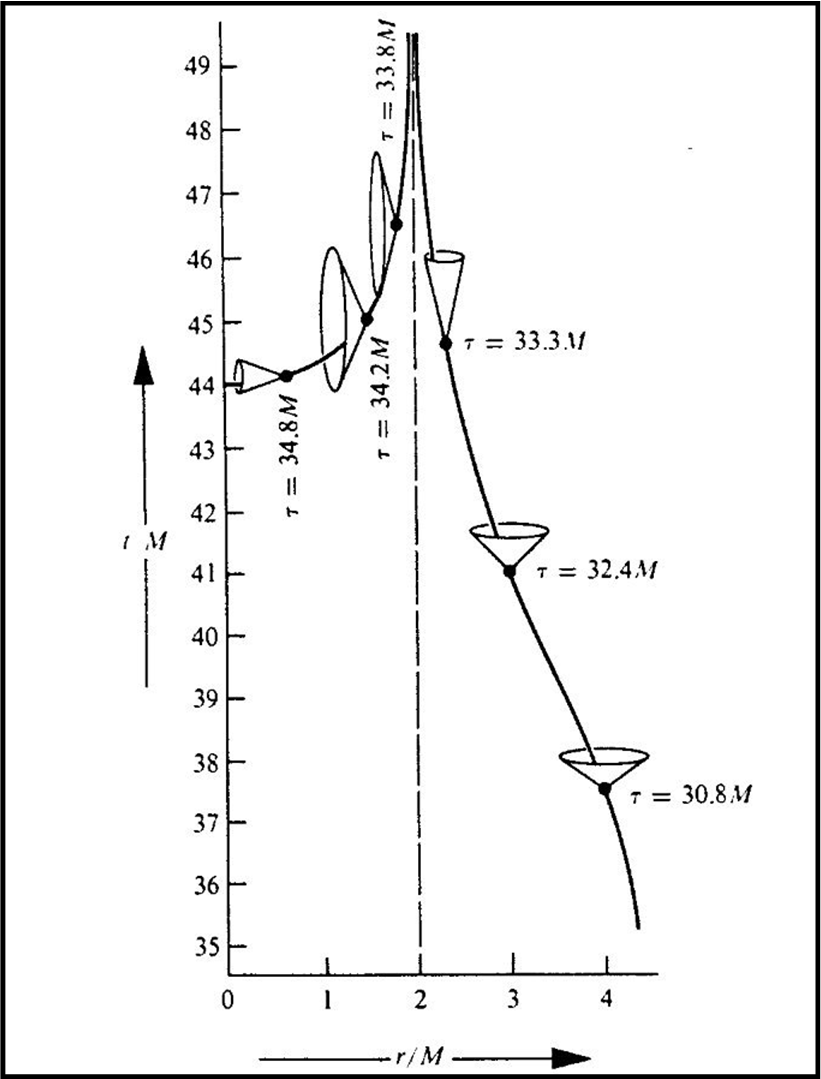
Vale la pena di riproporre una figura (Fig. 3), a cui tengo moltissimo, in cui si vede, in un diagramma di Minkowski, l’evoluzione di una stella massiccia che termina la sua esistenza come buco nero.

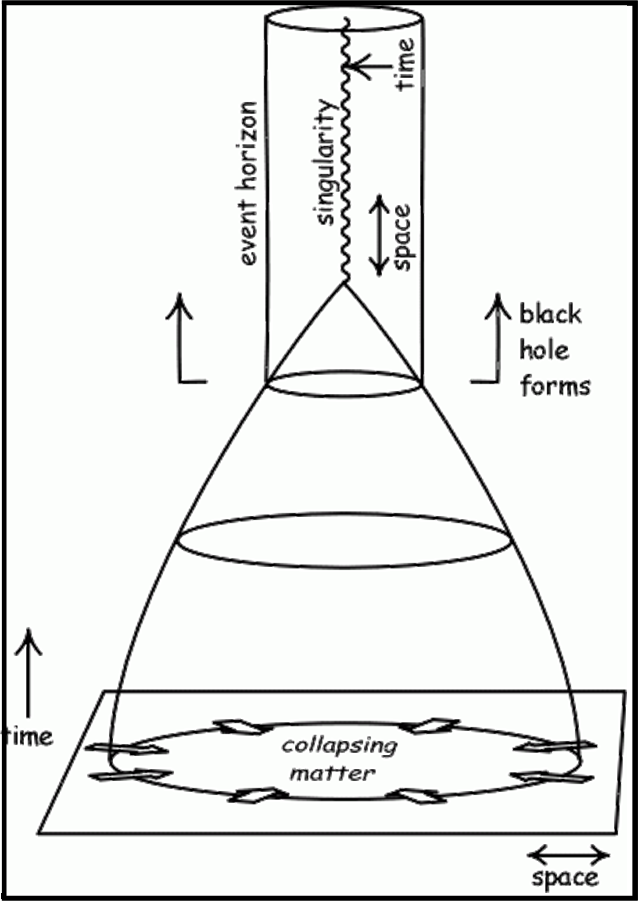
In qualche modo, la metrica di Schwarzschild ci permette di seguire la caduta dall’interno dell’orizzonte fino alla singolarità. Poi qualsiasi approccio deve fermarsi.

Questo è quanto si riesce a fare con la teoria della relatività generale. La teoria, infatti, non può descrivere gli effetti quantistici. La creazione teorica di una singolarità non va considerata come la formazione di un oggetto reale di volume zero e densità infinita, ma come un “errore” legato all’estensione di una teoria oltre i propri limiti di applicabilità. Qualsiasi previsione è quindi priva di senso. La battaglia tra gravità e materia nelle sue estreme condizioni è un qualcosa che la relatività non può affrontare. Per potere andare avanti sarebbe necessaria una teoria unificata, ossia una gravità quantistica, che, sfortunatamente, ancora non esiste.

Tuttavia, anche se impreparata a descrivere una singolarità (per sua stessa definizione), la RG permette, se trattata con la giusta metrica, di descrivere un buco nero come un oggetto macroscopico reale.

Minkowski perde i colpi

Cerchiamo di usare la metrica e lo spazio tempo di Schwarzschild e vediamo a cosa ci può portare.

In qualche modo dobbiamo rifarci alla rappresentazione di Minkowski, ossia ragionare in termini di una struttura causale. Questo significa che non si vuole considerare una semplice “collezione” di eventi, ma attaccare a ognuno di loro il relativo cono di luce, in modo da capire quali sono le possibili traiettorie percorribili da una certa particella che voglia avventurarsi verso un buco nero. Ricordiamo, infatti, se ce ne fosse ancora bisogno, che i coni di luce sono una rappresentazione causale, tale da mostrare quali eventi possano essere connessi causalmente e quali no.

Consideriamo, innanzitutto, uno dei punti chiave dello spaziotempo di Schwarzschild: la gravità piega verso la massa i coni di luce. In poche parole, l’asse del tempo si discosta da quello di un osservatore lontano e si inclina verso l’orizzonte degli eventi.

Un problema non da poco per lo spaziotempo di Minkowski… Noi proviamo lo stesso ad usarlo, piegando i coni di luce, anche se è cosa non “regolare”. Questa operazione poco lecita, ci permette, però, di ricavare in modo molto grossolano (e non privo di errori…) la traiettoria, vista da un sistema in quiete, di una particella che cada verso un buco nero e che prosegua nella sua caduta verso la singolarità

Finché restiamo fuori da lui, il piegamento del cono di luce è tale che è sempre possibile immaginare una traiettoria futura che permetta alla particella di scappare dalla massa che l’attrae, anche se, più vicini si va e più ardua è la fuga.  Giunti sull’orizzonte degli eventi  non vi è più possibilità di uscita, dato che la stessa luce è intrappolata sul raggio di Schwarzschild. Al limite, essa potrebbe stare in quella posizione (in linea di principio), ma non potrebbe uscirne. Nessun evento esterno appartiene al suo cono di luce futuro e quindi non è causalmente connesso alla particella.

All’interno del raggio di Schwarzschild, il cono di luce è talmente piegato che esso punta verso la singolarità. Non solo non è possibile tornare verso l’esterno, ma la strada che si può percorrere è una e una sola: quella verso la singolarità. In particolare, non è più possibile restare fermi.

Il raggio di Schwarzschild diventa un confine molto netto che separa eventi futuri che possono essere causalmente connessi ad altri eventi, da quelli che non hanno più possibilità di scelta: l’unico evento che possono raggiungere è la singolarità. Questa peculiarità del raggio di Schwarzschild (una porta da cui si può solo entrare) fa sì che il raggio di Schwarzschild prenda il nome di orizzonte degli eventi.

La sua definizione più corretta è quindi: una superficie sulla quale i coni di luce sono piegati a tal punto che non può essere percorsa nessuna traiettoria causale futura.

All’interno dell’orizzonte degli eventi si ha un vero e proprio passaggio di consegne tra spazio e tempo. Qualsiasi traiettoria può anche essere rallentata, ma la sua fine porta sicuramente nella singolarità. Le traiettorie tipo spazio avvengono verticalmente, mentre quelle tipo tempo  (casuali) avvengono orizzontalmente.

Vediamo di rappresentare, in modo molto grossolano e anche non corretto, cosa succede lavorando sullo spazio di Minkowski. Un approccio, del tutto personale, che porta con sé gravi inesattezze, ma che, in qualche modo, conforta la vera azione descritta dalla metrica di Schwarzschild.

In Fig. 4, siamo nello spaziotempo di Minkowski e l’orizzonte degli eventi è contrassegnato da due linee verticali che hanno nel punto di mezzo la singolarità.

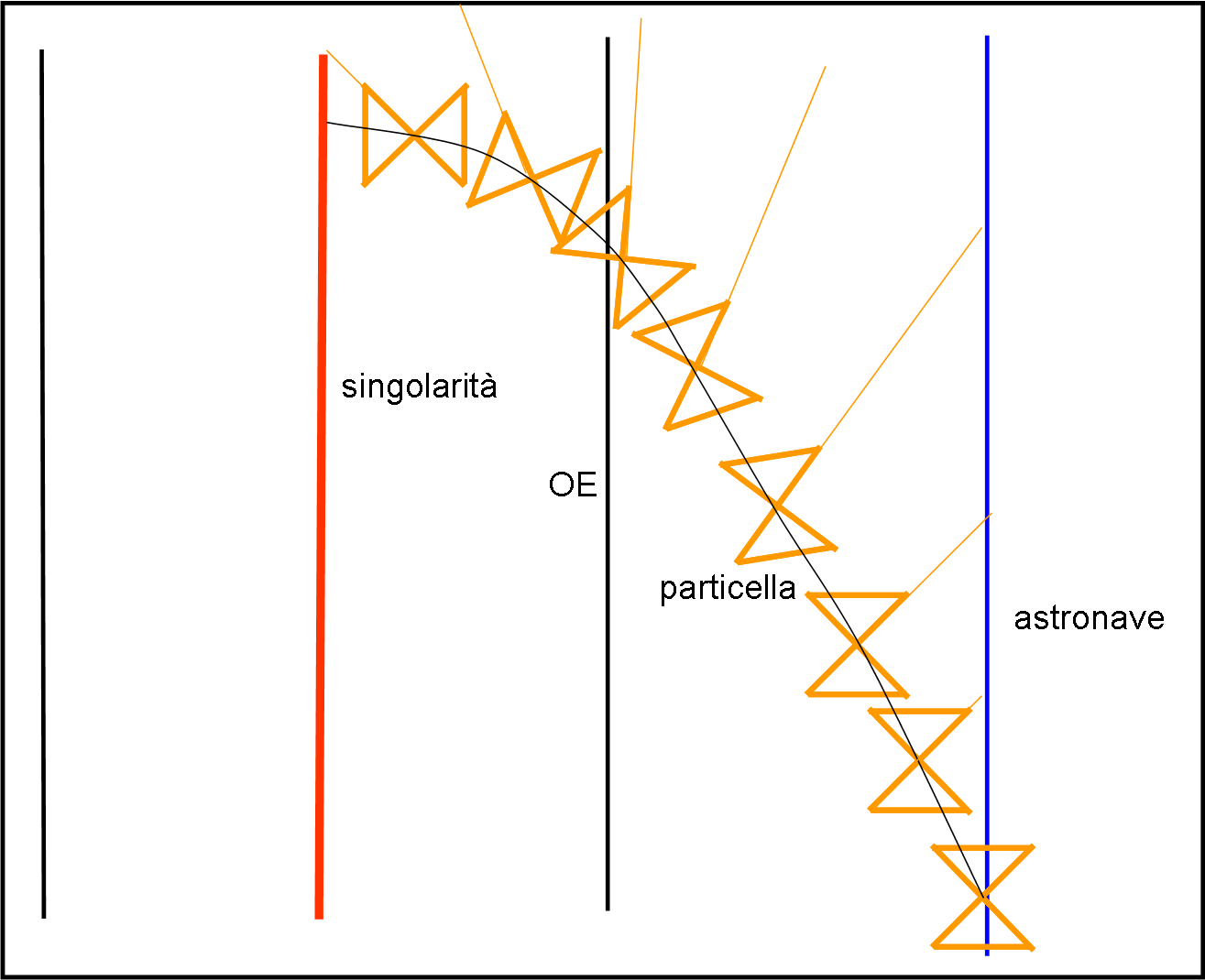
Prendiamo una traiettoria qualsiasi della nostra particella (in qualche modo vista dal suo sistema) e vediamo cosa fa la luce che essa potrebbe emettere a intervalli costanti. In condizioni di riposo assoluto vi è un’astronave che aspetta di ricevere i segnali luminosi periodici dalla particella esploratrice. Fino a che il cono di luce di quest’ultima non sia influenzato dalla gravità del buco nero e, quindi, non venga costretta a seguire la metrica di Schwarzschild, i suoi segnali luminosi giungono nel tempo previsto e l’astronave madre può seguire la traiettoria causale della particella (a lei parallela). Poi, piano piano il cono di luce si piega e il segnale luminoso inizia ad arrivare con un ritardo sempre maggiore.

La traiettoria che vede l’astronave madre è un qualcosa che tende ad andare al punto all’infinito della linea che delimita bordo esterno dell’orizzonte degli eventi. In altre parole la traiettoria vista dal sistema in quiete è una curva che tende asintoticamente all’orizzonte degli eventi, come mostrato in Fig. 5. Ciò comporta il ben noto fatto che un osservatore esterno non vedrà mai cadere qualcosa all’interno del buco nero. Essa sembrerà rallentare e fermarsi al suo bordo esterno. Altri effetti, come l’arrossamento della luce, la farà, infine, scomparire alla vista.

Portiamoci, adesso all’interno dell’orizzonte degli eventi, dove la nostra particella è realmente entrata senza subire nessun contraccolpo. Il suo cono di luce continua a piegarsi e la sua luce (sempre che abbia senso parlarne) va in verso contrario a prima se vista dalla singolarità. In altre parole sembra che la navicella provenga dall’infinito futuro. Tuttavia, non dimentichiamoci che il vecchio tempo è ormai uno spazio e, quindi, la particella continuerebbe nel suo movimento spaziale da destra verso sinistra, il tutto ribaltato di 90°.

Non voglio complicare ulteriormente le cose che andrebbero viste e spiegate solo attraverso la metrica utilizzata. Molto meglio, tralasciare visioni un po’ paradossali e rifare la figura nel modo corretto, basato sulla metrica di Schwarzschild, pur accettando dati di fatto altrettanto paradossali.

La Fig. 6  mostra la traiettoria esterna come vista dall’astronave madre e poi quella interna, derivata dalla metrica di Schwarzschild e si può notare come il piegamento dei coni di luce può essere rappresentato da un cambiamento della loro forma.

In modo concettuale (non matematico) possiamo dire che la larghezza del cono di luce di un evento è collegata alle sue possibili traiettorie future. Se è largo, le possibilità aumentano rispetto al caso di un cono stretto. Evitiamo di andare più a fondo, tralasciando il fatto che gli stessi coni di luce sono più o meno “lunghi”, adottando le classiche coordinate…

Quello che a noi preme sottolineare è che l’orizzonte degli eventi è una singolarità mai raggiungibile per le coordinate di Schwarzschild. In altre parole, questo vuol dire che nessun evento interno è connesso causalmente con un evento esterno futuro.

La Fig. 5 rende il tutto molto più schematico e comprensibile. La particella sale verso l’alto e raggiunge l’orizzonte degli eventi solo all’infinito, così come essa, proviene proprio dall’infinito (attenzione che la linea verticale non è più un tempo, ma uno spazio e che i coni di luce sono estremamente aperti tali da accettare traiettorie che sono ancora causali, come mostrato in Fig. 6).

Tante parole per concludere cosa? Molto semplice: l’utilizzo del diagramma di Minkowski, quando si utilizza la metrica di Schwarzschild, ci trascina verso quei famosi punti che siamo capaci anche di fotografare nella nostra realtà quotidiana (vedi le rotaie di una ferrovia), ma che sono difficili da trattare geometricamente. Stiamo, ovviamente, parlando dei punti all’infinito. D’altra parte ce lo dovevamo aspettare, dato che lo spaziotempo di Minkowski è qualcosa di infinito… Accidenti, proprio la parte più interessante, viene trascinata dove non può essere rappresentata.

Saremmo quasi pronti per il nuovo tipo di diagramma che impareremo a utilizzare, ma prima cerchiamo di descrivere con maggiori dettagli la metrica di Schwarzschild. Come detto chi vuole saltare questa parte lo può anche fare, avendo già dato i risultati più importanti. Tuttavia, è talmente bella che merita una lettura...

Lo spaziotempo di Karl Schwarzschild

Questo approfondimento dell'approfondimento lo dovevo a un genio come Schwarzschild, anche solo per il fatto di essere stato il primo a trovare una soluzione delle equazioni della relatività generale di Einstein. Inoltre, proprio la sua metrica viene utilizzata per poter descrivere ciò che capita all’interno dell’orizzonte degli eventi e dare il via ai diagrammi di Penrose (che introdurremo tra non molto). Non dimentichiamo, inoltre, che proprio la sua soluzione ha portato alla conoscenza degli attori più esotici del Teatro dell’Universo, i buchi neri. Ho dovuto limitare la descrizione alle parti maggiormente divulgabili, tralasciando le parti più “matematiche” e complesse. Spero che i concetti generali siano comunque facilmente comprensibili. Per i più esperti ho riportato i link a un paio di articoli che mi sembrano veramente completi.

Un breve richiamo

Cominciamo richiamando in modo ultra semplificato alcuni concetti base che abbiamo imparato dalla Relatività Ristretta (RR) e dalla Relatività Generale (RG).

Se non vi sono masse in giro lo spaziotempo può essere considerato piatto ed è perfettamente descritto dalla RR e dal diagramma di Minkowski. Possiamo anche spingerci un po’ oltre e dire che la relatività ristretta si può applicare tranquillamente, se non ci si avvicina troppo ai corpi celesti, soprattutto se molto massicci. In altre parole, essa ci permette di scrivere le equazioni del moto (e non solo) per oggetti che si muovano a velocità costante, senza subire accelerazioni come quella di gravità.

Già con questa semplificazione scopriamo che spazio e tempo non possono separarsi e quello che fa uno dei due influenza senza scampo ciò che fa l’altro. Non solo, però… descrivendo la dinamica si arriva nientedimeno che alla formula più famosa della Fisica, quella che ci dimostra in modo semplice e immediato che massa ed energia sono la stessa cosa. E dico poco…

Una rivoluzione fantastica che permette di studiare fisicamente le azioni delle particelle più piccole, per le quali la velocità della luce non è un meta tanto lontana. Ricordiamo, tra l’altro, che riducendo le velocità relative si ricade senza problemi nella meccanica newtoniana: un punto assolutamente da non trascurare e che dimostra come la RR non distrugga assolutamente la meccanica newtoniana, ma la amplifichi e raffini.

Nello spaziotempo relativistico al posto della distanza delle tre dimensioni nasce un invariante che lega le quattro coordinate e che sembra prendere a calci il teorema di Pitagora quando viene disegnato nel diagramma di Minkowski. Teniamolo bene a mente perché è proprio lui che ci permetterà di descrivere in modo “semplice” la geometria di Karl. Questo invariante diventa la “distanza” tra due eventi (e non due punti) nello spaziotempo a quattro dimensioni.

Fin qui tutto bene… ma cosa capita quando una certa massa fa sentire la sua gravità? Per Einstein il problema si risolve cambiando la geometria dello spaziotempo. Niente di veramente speciale a parole, ma incredibile nella sua genialità e perfezione. Lo spaziotempo si curva, Euclide va a farsi benedire e la semplice legge di Newton (F = ma) diventa leggermente più complicata, nascondendo al suo interno ben 16 equazioni all’apparenza irrisolvibili. Tuttavia, dentro di loro c’è tutto per capire cosa succede in un ambiente in cui la gravità entra in gioco e domina il moto delle particelle. Esse descrivono l’ambiente in cui fa la sua comparsa la materia e permette di stabilire il moto di chi si immerge al suo interno e viceversa.

Riflettiamoci sopra e pensiamo alle onde gravitazionali, ad esempio. Basta tener conto che due masse immense si muovano accelerando secondo traiettorie descritte perfettamente dalle equazioni ed ecco che ne esce fuori una vibrazione dell’intera struttura spaziotemporale. In fondo è estremamente banale, una volta che l’ambiente è stato descritto per qualsiasi configurazione possibile. Banale, generale, preciso e, quindi… geniale!

Semplificando di molto, basterebbe dire che le equazioni di Einstein determinano la geometria dello spaziotempo in funzione della materia che è contenuta al suo interno. Questa geometria permette, infine, di determinare il moto della materia. Cari amici, non potremo mai smettere di stupirci… e chi dice che Einstein ha recuperato “pezzi” a destra e a sinistra, ordinandoli secondo un unico schema, dovrebbe pensare alla Gioconda (o a quello che preferite): essa presenta un volto, un sorriso, uno sfondo paesaggistico, qualche tocco di pennello più o meno accentuato, un mix di colori… cose che tutti potevano conoscere, vedere e toccare. Eppure uno solo è riuscito a rendere la Natura sotto forma di essere umano, una trasformazione che si realizza continuamente sotto gli occhi di chi l’ammira. No, con la relatività, Einstein ha creato un capolavoro artistico e non solo scientifico.

Torniamo a noi…

Ricordate quanto avevamo fatto partendo dalla legge di Newton per arrivare alle leggi di Keplero, determinando le equazioni del moto? Non era stata cosa molto facile (e non parliamo del problema dei tre corpi)… Bene, le equazioni di Einstein permettono di fare la stessa cosa in modo ben più generale e completo, per qualsiasi configurazione geometrica della materia.

Non prendetevela se ribadisco un concetto ormai ben conosciuto, ma che può sempre essere in agguato e creare fraintendimenti e conclusioni errate. Sia nella RR che nella RG siamo sempre in uno spaziotempo a quattro dimensioni. Non facciamoci illudere dal diagramma di Minkowski in cui lo spazio si limita a una sola dimensione. In quel caso, lo spaziotempo è piatto non perché usiamo il piano del foglio, ma perché , la sua geometria e “quasi” euclidea e non risente di curvature. Nella RG lo spaziotempo si curva, ma le sue dimensioni restano sempre quattro.

Pensare di rappresentare con delle figure realistiche queste varie situazioni è impossibile. Abbiamo dovuto e dovremo utilizzare diagrammi “di comodo” che permettano di evidenziare i parametri fondamentali in modo intuitivo, escludendo, però, qualsiasi facile estrapolazione alla realtà effettiva. Abbiamo già fatto vedere (QUI) come la forma a imbuto che spesso descrive graficamente un buco nero porti spesso a interpretazioni e convinzioni completamente errate (e la metrica di Karl va proprio in quella direzione), anche se permette a chi la comprenda appieno di stabilire relazioni perfettamente valide.

Non per niente, il grande Feynman (e io l’ho seguito disciplinatamente) aveva preferito utilizzare una piastra a calore crescente verso l’esterno per definire la curvatura dello spaziotempo e non la solita sfera che mischia la forma di un  oggetto massivo con la deformazione spaziotemporale. Uno spaziotempo curvo è un ambiente in cui non vale la geometria euclidea. La superficie sferica è solo un  esempio a due dimensioni di ciò che deve essere estrapolato alle quattro dimensioni. Non confondiamoci, mi raccomando…

Appena pubblicata la RG, Einstein aveva utilizzato un’approssimazione abbastanza brutale per fornire ai colleghi prove osservative della sua teoria, attraverso, soprattutto, la deflessione della luce. Lui stesso non era molto convinto che si riuscissero veramente a risolvere le sue equazioni, ben sapendo che cosa contenessero: una specie di scrigno di perle con un chiavistello a prova di qualsiasi ladro. E, invece, il primo ladro giunse quasi subito… e il suo nome era proprio Karl Schwarzschild.

Un genio sfortunato

L’inizio della sua vita sembrava portarlo a una carriera prodigiosa. Nato nel 1873 arrivò al dottorato nel 1896, dopo aver già pubblicato due lavori molto importanti a soli 16 anni. Divenuto professore universitario, lavorò con Minkowski e Hilbert e in breve ottenne l’incarico più prestigioso per uno scienziato tedesco di quei tempi: la direzione dell’Osservatorio Astrofisico di Postdam. Nel 1914 scoppiò la guerra e Karl, ebreo, volle dimostrare il suo attaccamento alla Germania e partì per il fronte. Si comportò molto bene, ma il suo contributo alla patria durò ben poco, in quanto nel 1915 contrasse un terribile morbo della pelle che lo costrinse a entrare in un ospedale vicino al fronte russo. Per passare il tempo, Karl si mise a leggere la teoria di Einstein appena uscita e trovò subito una soluzione delle sue equazioni per un caso molto particolare, ma sufficiente per mettere in luce (si fa per dire) i buchi neri! Scrisse subito a Einstein, inviandogli i suoi calcoli e dicendo: “Come vedete la guerra mi ha trattato abbastanza gentilmente, permettendomi di stare lontano dal fuoco diretto e lasciandomi libero di percorrere questo sentiero nella terra delle vostre idee”. Karl morì sei mesi dopo.

Le ipotesi di Karl

 Ciò che Karl ha fatto è facilmente esprimibile: descrivere lo spaziotempo nei dintorni di una stella o, in generale, di una massa non trascurabile, utilizzando le equazioni di Einstein. Per far ciò ha cercato di semplificare al massimo le ipotesi di partenza. In particolare ha assunto che:

1) Nello spaziotempo considerato esiste solo una massa non trascurabile. Un qualcosa che richiama ciò che capita attorno al nostro Sole, dove la presenza di pianeti e di altra materia diventa del tutto insignificante. In altre parole, l’unica gravità che entra in gioco è quella del Sole o di chi per lui. Non esiste altra massa o energia al di fuori di quella della massa centrale. Il sistema considerato è, quindi, considerato vuoto.

2) La massa presente nello spaziotempo è perfettamente sferica. Questa ipotesi significa che se guardassimo una sfera da una certa distanza rispetto al suo centro, la metrica che misura la gravità, rimarrebbe sempre la stessa. In poche parole, lo spaziotempo è sfericamente simmetrico nelle varie direzioni spaziali.

3) Niente cambia nello spaziotempo rispetto al tempo, ossia lo spaziotempo è statico. In particolare, l’oggetto in questione non ruota e non possiede carica.

Tre assunzioni che non sono così pesanti come potrebbe sembrare a prima vista, ma che comportano semplificazioni enormi nelle equazioni di Einstein. Le 16 equazioni si riducono a una sola, la cui soluzione è esatta.

Sotto queste ipotesi, lo spaziotempo diventa completamente piatto a una certa distanza dalla massa. Più esattamente, esso tende a divenire piatto asintoticamente.

Riassumendo:

Karl intende esaminare e descrivere la geometria di uno spaziotempo all’interno e all’esterno di un corpo sferico che non si muove, non possiede carica, non ruota e non è assolutamente influenzato da azioni esterne. Uno scenario del tutto ideale. La stessa particella che si muove in questo contesto comporterebbe una minima ma sicura influenza. Tuttavia, il modello permette di approssimare in modo quasi perfetto molti oggetti dell’Universo reale, a partire dai singoli pianeti, passando per le stelle e finendo con oggetti del tutto esotici. Notiamo, infatti, che nessuna ipotesi viene fatta riguardo alla composizione del corpo centrale. Stelle di neutroni e buchi neri non sono perciò esclusi da questa trattazione.

La descrizione dello spaziotempo può essere diviso in due parti: quella esterna al corpo sferico e quella interna al corpo sferico. Il volume realmente occupato dal corpo celeste acquista, però, un significato diverso dal solito, dato che la massa viene misurata in … metri, come vedremo tra poco.

Le coordinate

Il primo passo da compiere è utilizzare un sistema di coordinate spaziali diverso da quello cartesiano (x,y,z) comunemente usato. Molto meglio, infatti, affidarsi alle coordinate polari, data la simmetria sferica. Il sistema di coordinate spaziali (a un certo tempo t) è quello rappresentato in Fig. 1.

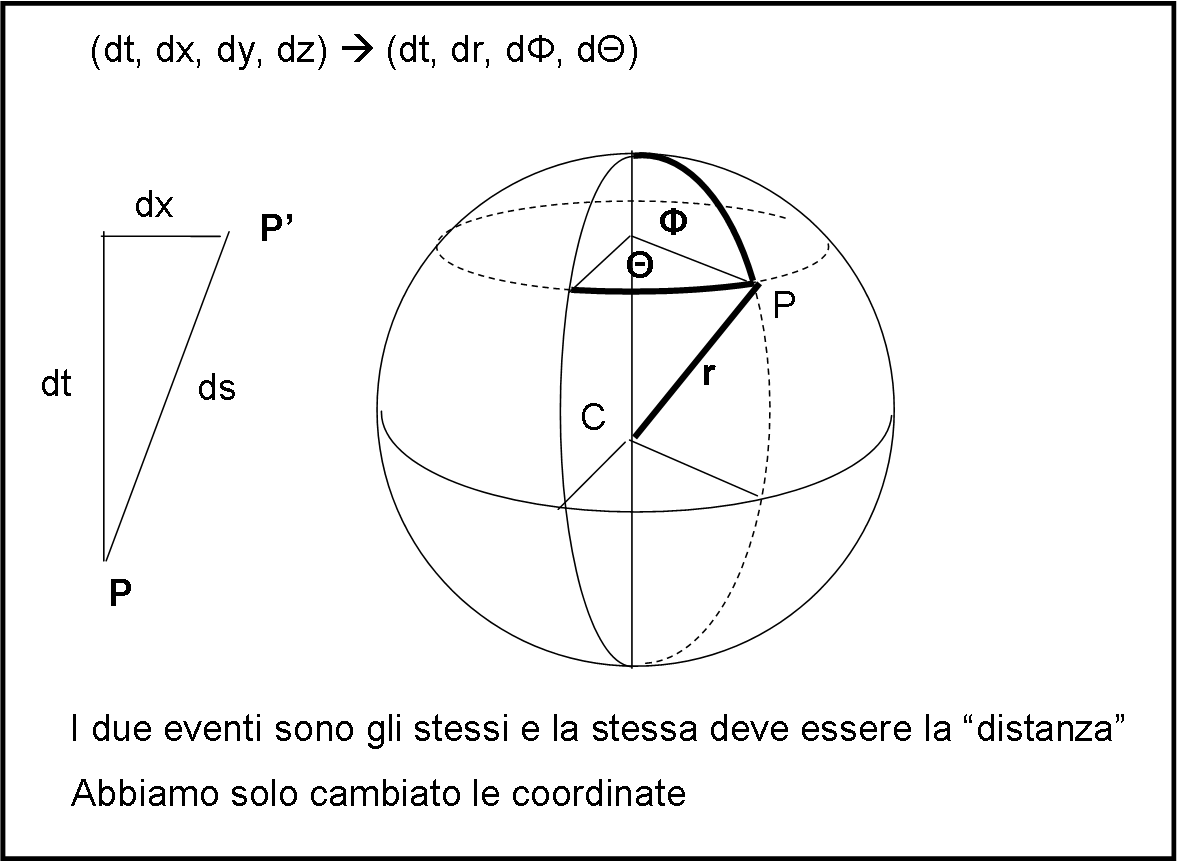
Recuperiamo dalla nostra memoria l’invariate a quattro dimensioni della RR (non dimentichiamoci il tempo, mi raccomando!) e scriviamolo nelle coordinate x,y,z,t:

ds² = dt² – dx² – dy² – dz²

Esso indica la “distanza” spaziotemporale tra due eventi e vale per qualsiasi sistema di riferimento, proprio come la distanza euclidea rimane se stessa pur cambiando sistema di coordinate. Sulla base della Fig. 1, l’invariante prende la forma:

ds² = dt² – dr² – r² dΦ² – r²sin²Φ dΘ²

che possiamo anche scrivere:

ds² = dt² – dr² – r² (dΦ² + sin²Φ dΘ²) = dt² – dr² – r² d²Ω        …. (1)

Notiamo che il differenziale d²Ω non è altro che l’elemento di superficie di una sfera unitaria, per cui non dipende dal raggio. Sarà un fatto molto importante tra poco.

La formula appena scritta descrive l’invariante in uno spazio “vuoto, privo di masse. Ne segue che, dopo aver descritto la geometria di Karl (valida nella RG) dovremmo trovare, per distanze molto alte rispetto al centro del corpo celeste sferico, che l’equazione di Einstein si riduce alla (1).

Costruiamo, adesso, una massa molto speciale, cambiando le sue unità di misura. Facciamo un qualcosa di simile a quanto utilizzato nella RR maneggiando il tempo. Ricordiamo che l’avevamo moltiplicato per c (costante) e avevamo costruito un  tempo che veniva misurato come una distanza spaziale. Infatti:

T = t·c => s·m/s = metri

In altre parole, il tempo veniva misurato in metri e diventava una coordinata non diversa dalle altre tre.

Adesso facciamo qualcosa di simile per la massa del corpo celeste. Moltiplichiamola per G (costante di gravità universale) e dividiamola per c². Si ottiene:

M = m G /c² => (kg) (m³/kg s²) (s²/m²) = metri

Piccolo miracolo… e abbiamo ottenuto una massa misurata in metri.

Vi faccio subito divertire. Quanto vale nel caso del Sole? Essa diventa 1.5 km. Voglio solo ricordarvi, tanto per farvi riflettere un breve attimo, che il celebre raggio di Karl (orizzonte degli eventi) per il Sole risulta essere di 3 km. Proprio il doppio della sua massa espressa in metri… Un caso? Nemmeno per sogno. Abbiate pazienza e lo scopriremo…

La geometria

A questo punto non ci resta che immaginare il nostro Karl, malato nel suo letto di ospedale, che comincia a imporre le sue ipotesi restrittive alle 16 equazioni di Einstein. Uno dopo l’altro i vari tensori vanno a zero o giù di lì e ciò che resta ha la seguente forma (espressa nelle coordinate e nelle unità di misura appena introdotte):

ds² = dt²(1 – 2M/r) – dr²(1 – 2M/r)^-1 - r² d²Ω     ….(2)

Prima di proseguire, vediamo subito cosa succede se r tende a infinito (ci portiamo molto lontani dalla massa centrale). 2M/r tende a zero, per cui la (2) diventa esattamente la (1), la distanza invariante nello spaziotempo piatto! Proprio quello che volevamo…

Riflettiamo sulla (1)

Se poniamo t e r costanti (dt e dr vanno a zero), otteniamo la rappresentazione di una superficie sferica “normale”. Al variare di r le sfere sono una interna all’altra come una specie di matrioska. Lo spaziotempo di Karl è quindi descritto lavorando su sfere di raggio decrescente e poco importa quale sia il vero volume del corpo celeste sferico iniziale, dato che compare solo una massa misurata in metri. Possiamo perciò arrivare tranquillamente fino al valore “limite” di M, che rappresenta la massa del corpo celeste nelle nuove unità di misura. Possiamo, quindi, dire che giungiamo tranquillamente fino alla parte esterna del corpo la cui massa è espressa in metri come il suo raggio.

Attenzione, però, a non commettere un errore madornale. Questa serie di sfere “normali” appaiono tali solo per un osservatore posto molto lontano da loro, ma non certo per chi si muove su di esse. Il righello e l’orologio di quest’ultimo subiscono variazioni sempre più grandi mano a mano che si avvicinano a M (misurata in metri).

Fissiamo, ad esempio, tutte le coordinate e facciamo variare solo il raggio r (tutte le altre differenze vanno a zero). Quello che si ottiene è una sezione dello spazio:

dσ² = – dr²(1 – 2M/r)^-1    …. (3)

L’ho chiamata dσ dato che è una distanza puramente spaziale.

Il diagramma embedding

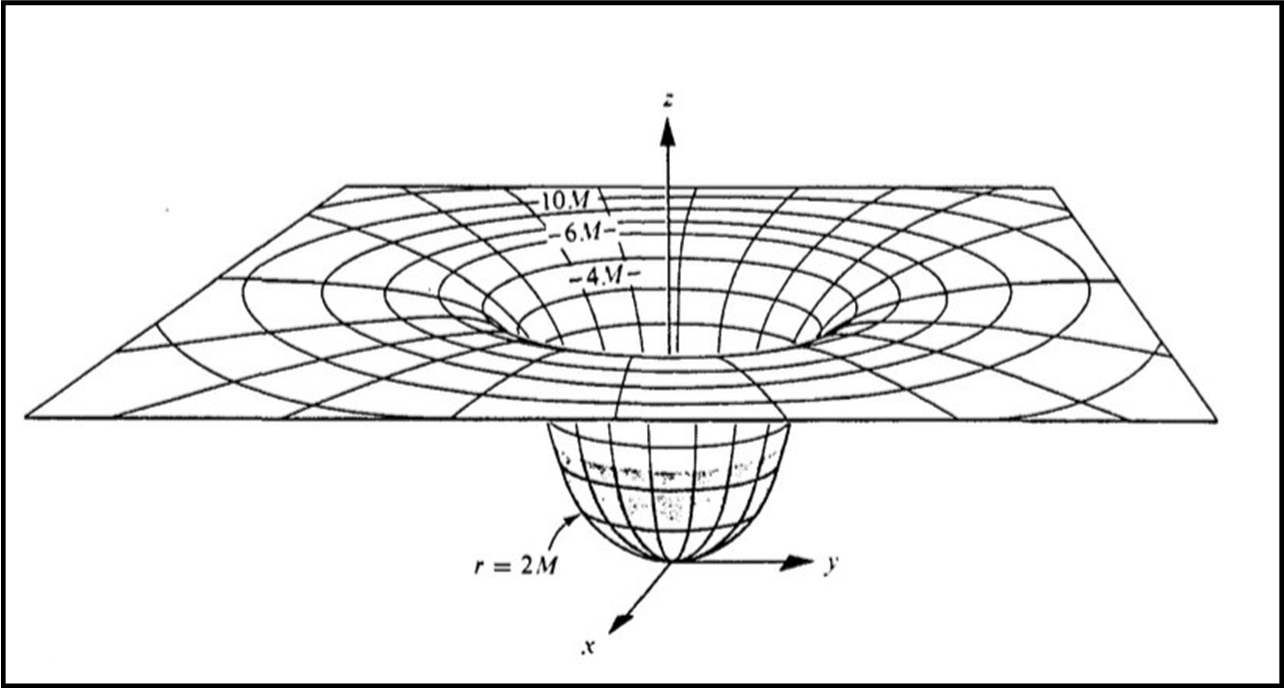
Se noi diminuiamo la coordinata r in modo costante tra due sfere adiacenti, otteniamo un dσ che aumenta sempre di più, . In altre parole, più vicini andiamo al valore M e più le sfere concentriche si allontanano tra di loro. Tutto ciò può essere rappresentato in Fig. 2, che ci fa subito ricordare il celebre imbuto dei buchi neri (in fondo è la stessa cosa).

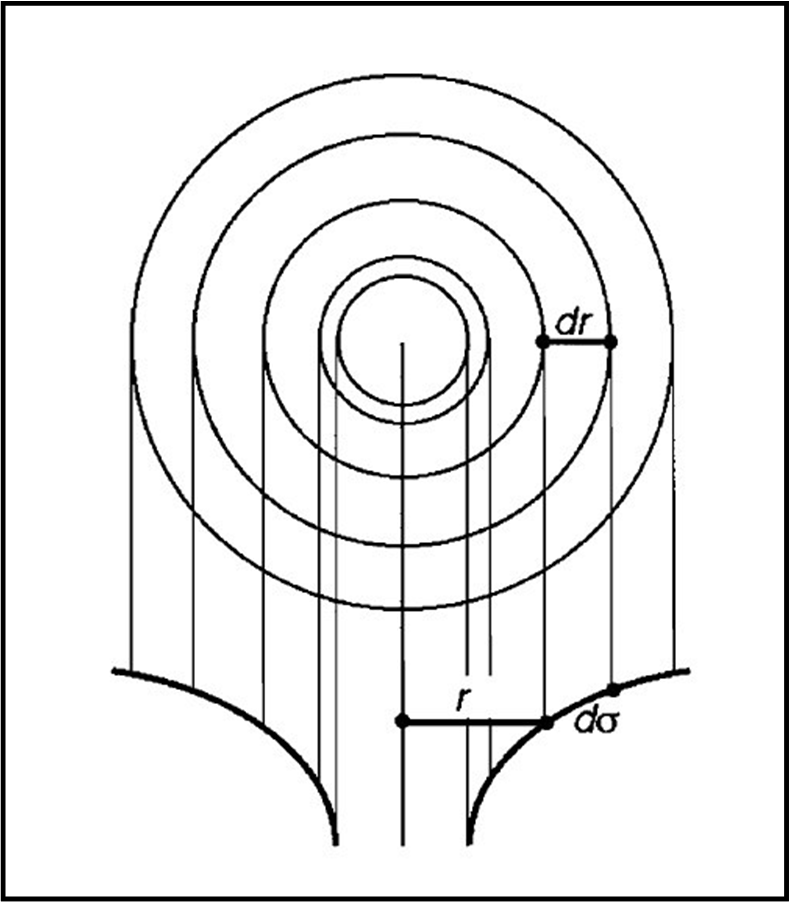
In realtà, tutto si basa sul fatto che misurare un raggio dividendo la circonferenza equatoriale per 2π non è la stessa cosa che misurare il raggio stando sulla superficie sferica (QUI e QUI).

Descriviamo la faccenda in maniera più realistica. Immaginiamo di essere molto distanti dalle sfere concentriche e fissiamoci sui loro cerchi equatoriali. Essi ci appariranno perfettamente equidistanti tra loro per separazioni costanti del raggio. In altre parole, ogni raggio è legato alla circonferenza equatoriale dalla formula 2πr o -se preferiamo- alla superficie sferica dalla relazione 4πr². Da lontano, la metrica di Karl sembra un gioco da bambini… Tuttavia, la situazione è ben diversa per chi misura le distanze PROPRIE (fisiche), viaggiando tra le sfere. La relazione tra le distanze dr misurate tra due sfere da un osservatore all’infinito e quelle dσ misurate localmente per le stesse due sfere è data proprio dalla (3).

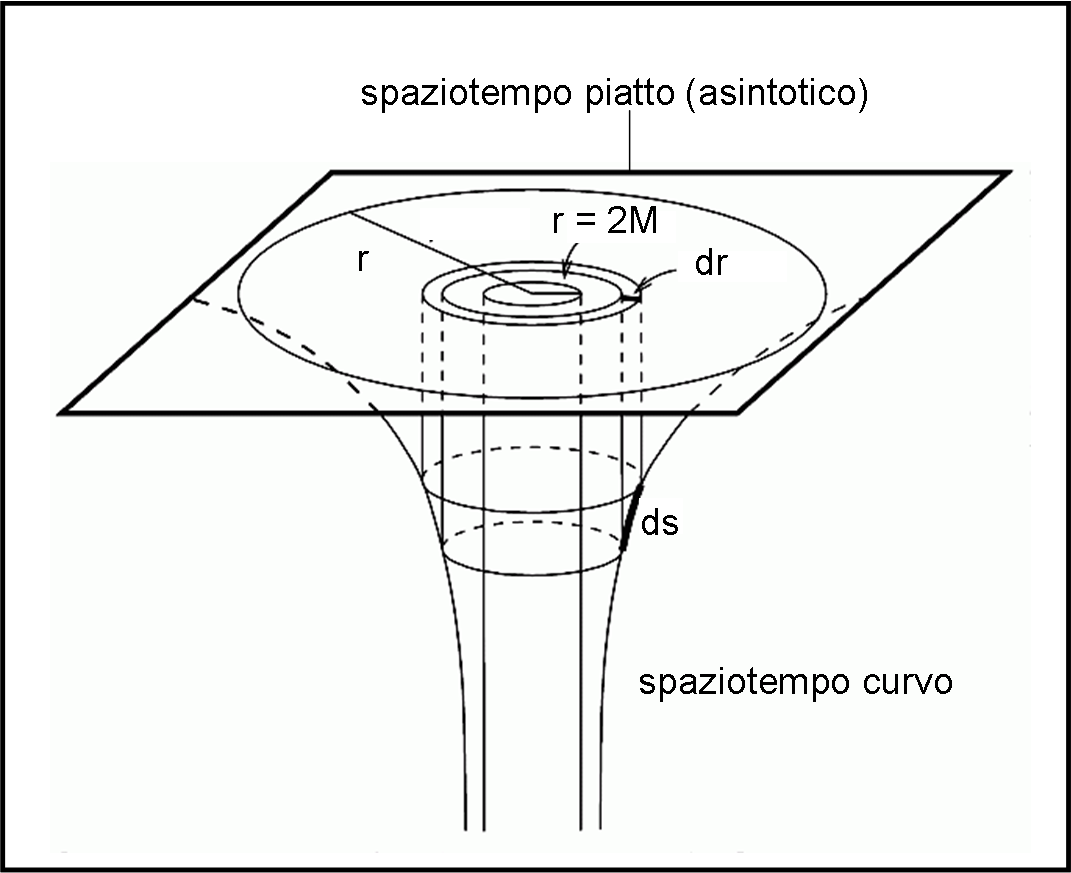
In modo più generale (tenendo conto anche del tempo), si deve ricordare che tutte le misure di spazio e tempo sono puramente locali, ossia dipendono dal righello e dall’orologio di chi appartiene a uno spaziotempo curvo. Le coordinate di partenza (all’infinito) e quelle locali (proprie) sono legate in modo non banale dalla metrica di Karl, in uno spaziotempo curvo. Tutto ciò può essere raffigurato in un diagramma a tre dimensioni proiettato su due dimensioni, con i limiti concettuali (tutto è, fuorché una rappresentazione realistica) che ormai dovremmo conoscere molto bene. Si ottiene il diagramma detto embedding (incastrante o qualcosa del genere) dello spaziotempo di Schwarzschild, rappresentato in Fig. 3. In parole più semplici questo tipo di diagramma è a due dimensioni, ma è visualizzato (embedded) in uno spazio euclideo a tre dimensioni per rendere evidente la sua curvatura.

Analizzato lo spazio, pensiamo ora al tempo. Ciò che succede è abbastanza intuitivo… il tempo proprio locale è più piccolo del tempo misurato da lontano, dato che il fattore di curvatura è più piccolo di uno. Il che implica che la frequenza del segnale luminoso emesso da un certo evento risulti più piccola per un osservatore lontano. In poche parole, l’osservatore lontano vede una lunghezza d’onda maggiore, ossia subisce il redshift gravitazionale.

Avvicinandosi al valore limite di r (2M, ci torneremo sopra tra poco), il tempo proprio diventa sempre più piccolo rispetto a quello di un orologio lontano. Per quest’ultimo un singolo tic-tac dell’orologio locale tende a coprire un tempo infinito. Un segnale, perciò, mandato quando r = 2M, impiega un tempo infinito per raggiungere l’osservatore non immerso nello spaziotempo curvo. La sfera che corrisponde a questo valore di r è chiamata ORIZZONTE DEGLI EVENTI. Beh… l’abbiamo ritrovata, lavorando in modo “serio” con la metrica di quel genio di Karl.

Come piccolo (già noto) esercizio, vediamo come la “strana” massa M, possa anche ricavarsi facilmente senza entrare nella metrica di Karl, limitandosi alla velocità di fuga. Notiamo, però, che la vera definizione è data da Karl, ma che il risultato può essere trovato in modo semplificato (a posteriori).

Consideriamo il raggio di un corpo di massa M (normale) per il quale la velocità di fuga sia pari a c. Il problema si può risolvere attraverso l’energia cinetica e potenziale del corpo in questione.

E_c = ½ mv² = ½ mc²

E_P = h g m = h m GM/r²

Ma h = r, per cui:

E_P = mGM/r

Uguagliando le due energie:

½ mc² = mGM/r

r = 2GM/c²

Bene, abbiamo dimostrato che il raggio non è altro che la massa “modificata” moltiplicata per 2. Proprio quello che abbiamo trattato attraverso la metrica di Karl.

Non è difficile, inoltre, determinare la dilatazione del tempo attraverso la (2). Immaginiamo di essere fermi in un punto dello spaziotempo di Karl. In un piccolo intervallo attorno a noi possiamo considerarci nello spazio di Minkowski. Varrebbe quindi un invariante “classico” del tipo:

ds² = dt’² – dx² – dy² – dz²

dove t’ misura il nostro tempo proprio. Essendo fermi, deve valere dx = dy = dz = 0. In quel punto, però, l’invariante deve sempre essere lo stesso, sia per Karl che per Minkowski, per cui risulta (dalla (2)):

dt’² =  dt² (1 – 2M/r)

Ossia:

dt’ = dt (1 – 2M/r)^1/2

Notiamo come, pur essendo ormai in balia di uno spaziotempo dominato della RG, si possa studiare localmente la situazione, approssimandolo con uno spaziotempo di Minkowski. Chi ancora giudicasse la RR una teoria “secondaria” e non realistica sarebbe bene che rivedesse il proprio pensiero. In fondo il diagramma embedding è una serie di tanti piccoli tasselli “piatti” in cui valgono le leggi della RR (vedi Fig. 4).

L’orizzonte

Che il raggio r = 2M sia molto particolare si può subito dedurre dalla (2). Per tale valore la parentesi che moltiplica dr² va ad infinito e anche ds². Siamo di fronte a un punto singolare, quello che corrisponde al raggio di Karl o all’orizzonte degli eventi. Un  punto singolare che, però, dà un fastidio abbastanza relativo. Basta infatti cambiare sistema di coordinate per renderlo “inoffensivo”.

Un altro valore per cui ds² va ad infinito è r = 0. Per lui, purtroppo, non si può fare niente: siamo di fronte a una vera singolarità.

La singolarità che si ottiene all’orizzonte è dovuta alla scelta delle coordinate ed è tale solo per chi osserva da lontano e non per chi si trova veramente sulla sfera corrispondente. Ciò che realmente capita (e l’abbiamo già detto varie volte) è una trasformazione delle linee di tipo spazio in linee di tipo tempo. Diciamo meglio: al di fuori dell’orizzonte le linee radiali della geometria di Karl rappresentano intervalli spaziali. Al suo interno, invece, gli intervalli radiali diventano intervalli temporali. Lo stesso Einstein era rimasto molto imbarazzato dal limite dato dall’orizzonte e l’aveva considerato una vera barriera. In realtà, gli intervalli radiali di tipo tempo, all’interno dell’orizzonte, vogliono solo significare, concettualmente, che lo spazio cade verso la singolarità vera, con una velocità superiore a quella della luce. In altre parole, per rimanere spazialmente fermi dentro all’orizzonte bisognerebbe spostarsi a velocità maggiori della luce, il che è impossibile.   Siamo letteralmente trascinati lungo una linea temporale che porta inesorabilmente verso il punto in cui r = 0. Dobbiamo notare che questo cambiamento di linee (da tipo spazio a tipo tempo) è anch’esso legato alle coordinate utilizzate. Ad esempio, utilizzando quelle di Kruskal–Szekeres non vi sarebbe nessun passaggio da spazio a tempo… ma, la sua trattazione la lascio a chi vuole andare veramente per il sottile.

Il diagramma “embedding” completo è quello rappresentato dalla Fig. 5.

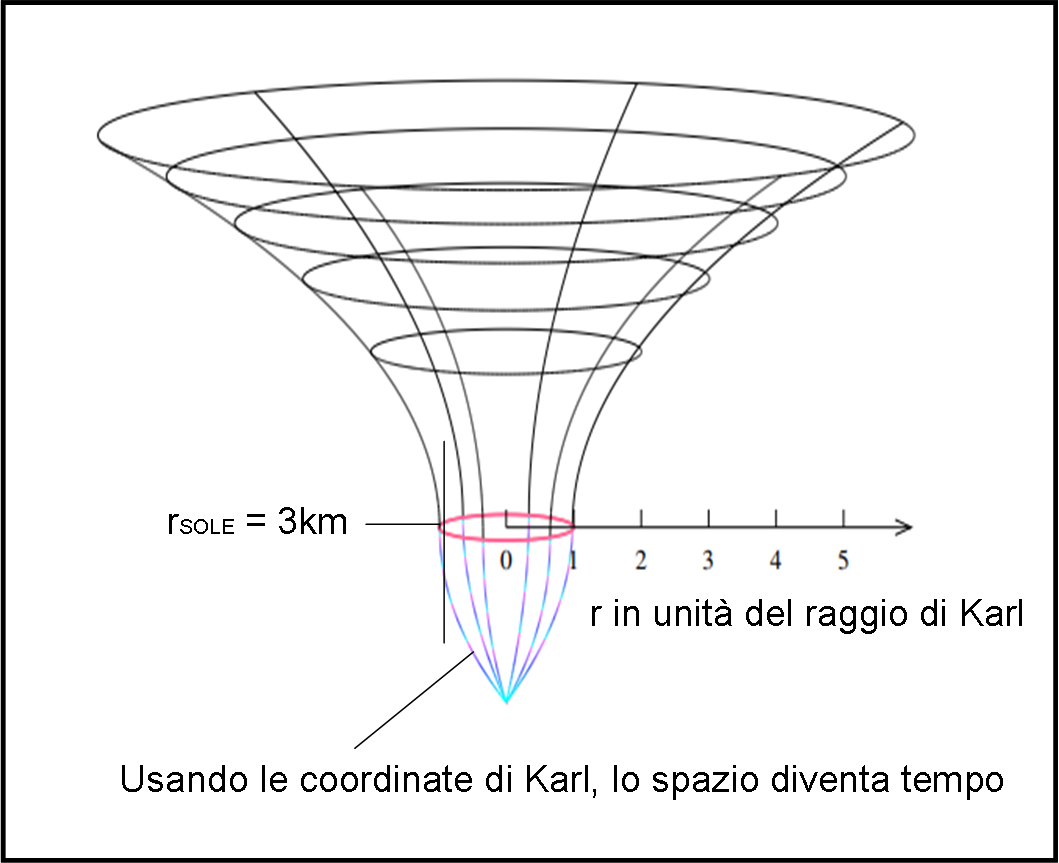
Ciò è vero anche per una stella qualsiasi e non solo per un buco nero (che deve avere la massa reale contenuta all’interno dell’orizzonte). Ricordiamo, infatti, che la massa del Sole, definita in metri, è pari a 1.5 km. Per r = 2M = 3 km, si entra effettivamente all’interno dell’orizzonte degli eventi del Sole e vale l’ultima parte del diagramma di Fig. 5. Tuttavia, il Sole sarebbe un buco nero solo se la sua vera massa fosse contenuta entro i 3 km di raggio.

Descrivere il cambiamento di coordinate per potere trattare la parte più “segreta” del diagramma non è cosa per noi, così come la derivazione della (2), e dobbiamo accettarle come un dato di fatto. Per chi volesse andare oltre, consiglio questo lavoro professionale, ma, nella rete, ve ne sono molti altri (in inglese) e qualcuno anche in italiano

Spero ardentemente che questa trattazione, giocoforza incompleta e semplificata, sia sufficiente a far capire lo splendido lavoro di Karl e quale enorme contributo abbia dato allo sviluppo della RG e alla sua comprensione, ancora non certo conclusasi.  Quanti Nobel avrebbe dovuto portare con sé questa stupefacente teoria, continuamente confermata, malgrado i mille e uno tentativi per trovarne delle crepe. Adesso, possiamo tornare, con maggiore tranquillità, al diagramma di Penrose e chissà che non si riesca a cambiare … Universo!

verso Penrose

Prima dell'approfondimento su Karl e la sua metrica avevamo  parlato dei punti all’infinito. D’altra parte ce lo dovevamo aspettare, dato che lo spaziotempo di Minkowski è qualcosa di infinito… Accidenti, proprio la parte più interessante, viene trascinata dove non può essere rappresentata! E chi l’ha detto? Basta concentrare uno spaziotempo infinito in uno spaziotempo finito, che sia perfino capace di mantenere gli angoli. Cosa possiamo volere di più? La metrica di Karl ci permette di descrivere le traiettorie avvicinandosi all'orizzonte e anche oltre. Ora non ci resta che compattare il tutto e fare "sparire" i punti all'infinito.

I buchi neri, a parte la difficoltà di trovare il miglior modo per rappresentarli, sono sicuramente  gli oggetti più perfetti dell’Universo (non l’ho detto solo io…). Bastano infatti tre soli parametri per caratterizzarli: massa, carica elettrica e momento angolare. Nel caso più semplice che stiamo trattando, ne basta uno solo: la massa. Questo fatto porta a una conclusione straordinaria e unica: qualsiasi sia il tipo di materia che forma un buco nero, degenere o non degenere, salata o non salata, solida o liquida, non ha alcuna importanza (un vero deposito i rifiuti, dove non interessa la differenziazione…). Le caratteristiche finali dell’oggetto non cambiano di una virgola. Qualsiasi informazione su ciò che è stato inghiottito viene persa. Questa peculiarità ha portato al ben noto slogan: “I buchi neri non hanno capelli (black holes have no hairs)”.

Un oggetto, perciò che potrebbe anche considerarsi estremamente semplice, almeno per quanto riguarda le sue proprietà fisiche. L’unica cosa che dobbiamo cercare di esprimere al meglio è il suo inserimento in un diagramma altrettanto semplice, che possa, alla fine, portare ben più lontano dello spazio che lo circonda.

Con la metrica di Schwarzschild siamo riusciti a descrivere sia l’interno che l’esterno di un buco nero (ossia fuori e dentro l’orizzonte), ma si può fare di meglio e di più. Traiettorie che possono solo andare o provenire dall’infinito, coni di luce che si piegano e/o si stringono. Difficoltà che possono e devono essere superate, qualsiasi siano le modalità di formazione. Ricordiamo, infatti, che il buco nero stellare deriva da una storia ben definibile (una massa si contrae fino a che il suo raggio diventa minore dell’orizzonte degli eventi). In realtà, però, non ci sarebbe nemmeno bisogno di una massa che si contragga, basterebbe avere una massa  tale che l’orizzonte degli eventi sia esterno alla sfera che la contiene. Il caso classico è quello dei buchi neri galattici. Non dimentichiamo, infatti, che il raggio di Schwarzschild dipende solo e soltanto dalla massa della sfera: il buco nero non ha capelli…

Ricordiamo, inoltre, che la metrica di Schwarzschild descrive, finché può, ciò che si vede da un sistema in quiete esterno, che non risenta del campo gravitazionale. Chi si avvicina al buco nero mostra a chi sta fermo un orologio che continua a rallentare, il che si traduce in qualcosa che non può raggiunge mai l’orizzonte degli eventi, se non all’infinito. In altre parole, una traiettoria che sembra dare sempre una possibilità di uscita a chi ha intrapreso un viaggio così rischioso.

L’orizzonte degli eventi rappresenta l’ultima via d’uscita, quella che è permessa solo alla luce. Non una vera via d’uscita, però, dato che la luce è costretta a restare sempre in quella posizione. E’ inutile che l’astronave aspetti il segnale di ritorno, dato che lo riceverà solo all’infinito. Permettetemi di azzardare un frase che potrebbe chiarire ciò che stiamo per andare a fare: l’orizzonte degli eventi è l’ultimo percorso effettuabile dalla luce prima di entrare nel buco nero.

Lo spaziotempo di Schwarzschild ammette, però, una soluzione ben più ampia. Detto in parole molto povere, la soluzione può essere ribaltata, cambiando il segno al tempo, con tutto ciò che ne può derivare. Avete sicuramente già capito di cosa sto parlando, ma ogni cosa a suo tempo.

Devo anticipare che sono stati fatti vari tentativi per descrivere lo spaziotempo attorno a un buco nero, partendo dalla metrica di Schwarzschild. Una piuttosto comune è quella che usa le coordinate di Kruskal–Szekeres. Attraverso una trasformazione di coordinate è come se si aprisse l’imbuto di Schwarzschild (al pari di un’anguria) e si appiccicasse su un piano. Ne viene fuori un diagramma simile a quello di Minkowski, estremamente interessante, ma che si porta dietro, comunque, i punti all’infinito che tutto hanno, meno che essere facilmente rappresentabili. Chi vuole andare a fondo di questa metrica, che già porta molto avanti, può leggere l’ottima spiegazione data su Wikipedia (inglese!) QUI

Il diagramma di Penrose

Noi, invece, facciamo un passo ancora più lungo, dato che siamo stati abituati a non spaventarci dei punti all’infinito, perfino quando abbiamo introdotto il corso di matematica elementare.

Guardiamo con occhio molto critico lo spaziotempo di Minkowski. Esso rappresenta uno spaziotempo infinito e, di conseguenza possiede molti punti all’infinito: quelli delle curve tipo spazio, quelle delle curve tipo tempo e quelle delle curve tipo luce.

Partiamo da lontano e costruiamo un diagramma semplicissimo, composto da due fasci di linee rette e parallele tra loro… (Fig. 7).

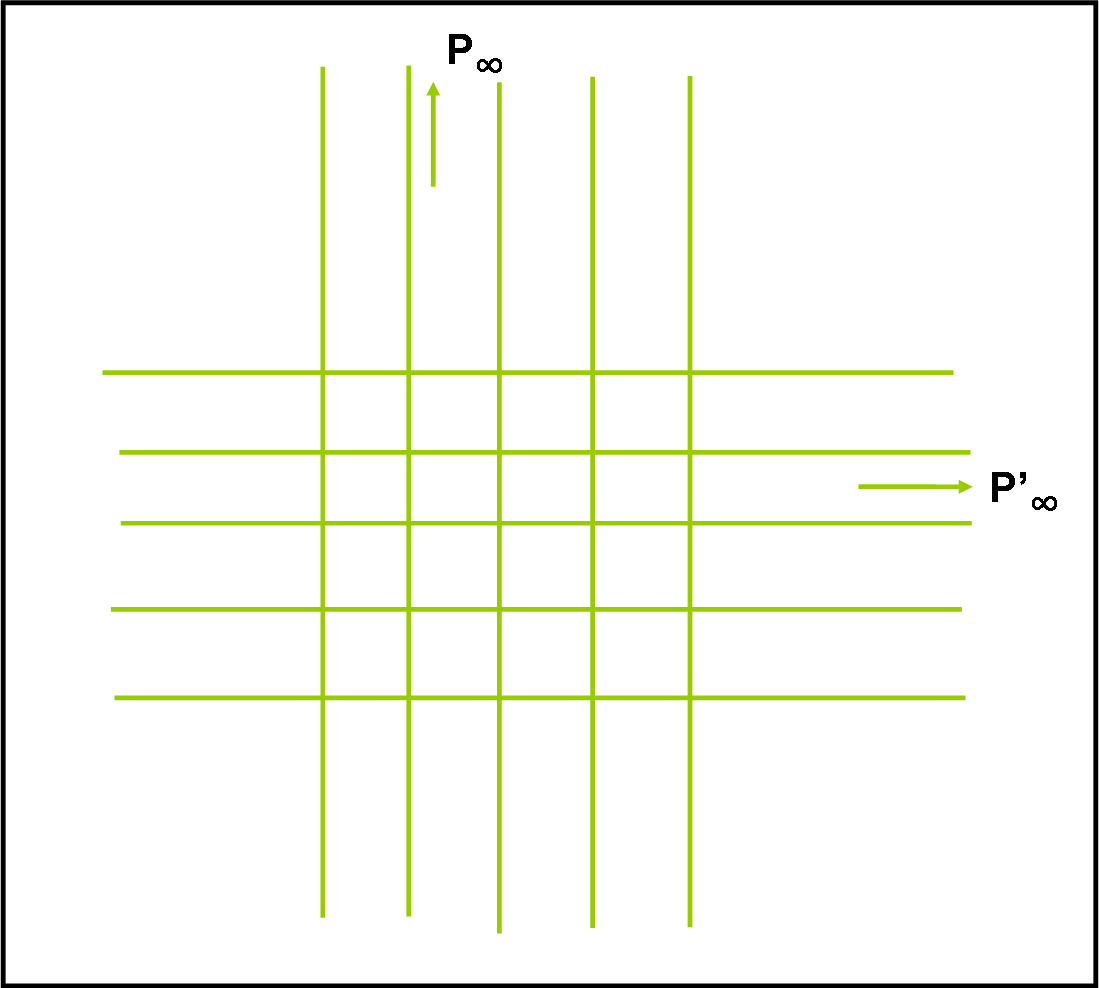
Tanti binari paralleli, in due direzioni perpendicolari. Vi è una tecnica tipica dell’architettura più sofisticata che riesce a disegnare ciò che vede un osservatore in qualsiasi punto si trovi: la prospettiva. In parole terra-terra, le rette verticali andranno tutte verso un punto all’infinito, così come quelle orizzontali (Fig. 8). Perché allora non disegnare questi punti immaginari come veri e propri punti? La linea che passa per loro la conosciamo molto bene, ed è la retta all'infinito.

Ovviamente le distanze sulle rette che portano a loro non si mantengono, nel senso che gli stessi segmenti vicini a noi sembrano molto più lunghi di quelli che vediamo in lontananza. Tuttavia, se a noi non interessasse la misura di ciò che osserviamo, ma solo la causalità degli eventi che vengono rappresentati, non sarebbe un grosso problema. Proviamo a estendere la rappresentazione anche “alle nostre spalle”, ossia i binari convergono non solo davanti a noi, ma anche dietro. Otteniamo così quattro punti all’infinito .  Immaginiamo, ancora, di considerare le linee verticali come linee del tempo e quelle orizzontali come linee dello spazio. La figura diventa un qualcosa di estremamente semplice: le linee verticali e orizzontali si curvano per finire nei punti all'infinito (Fig. 9).

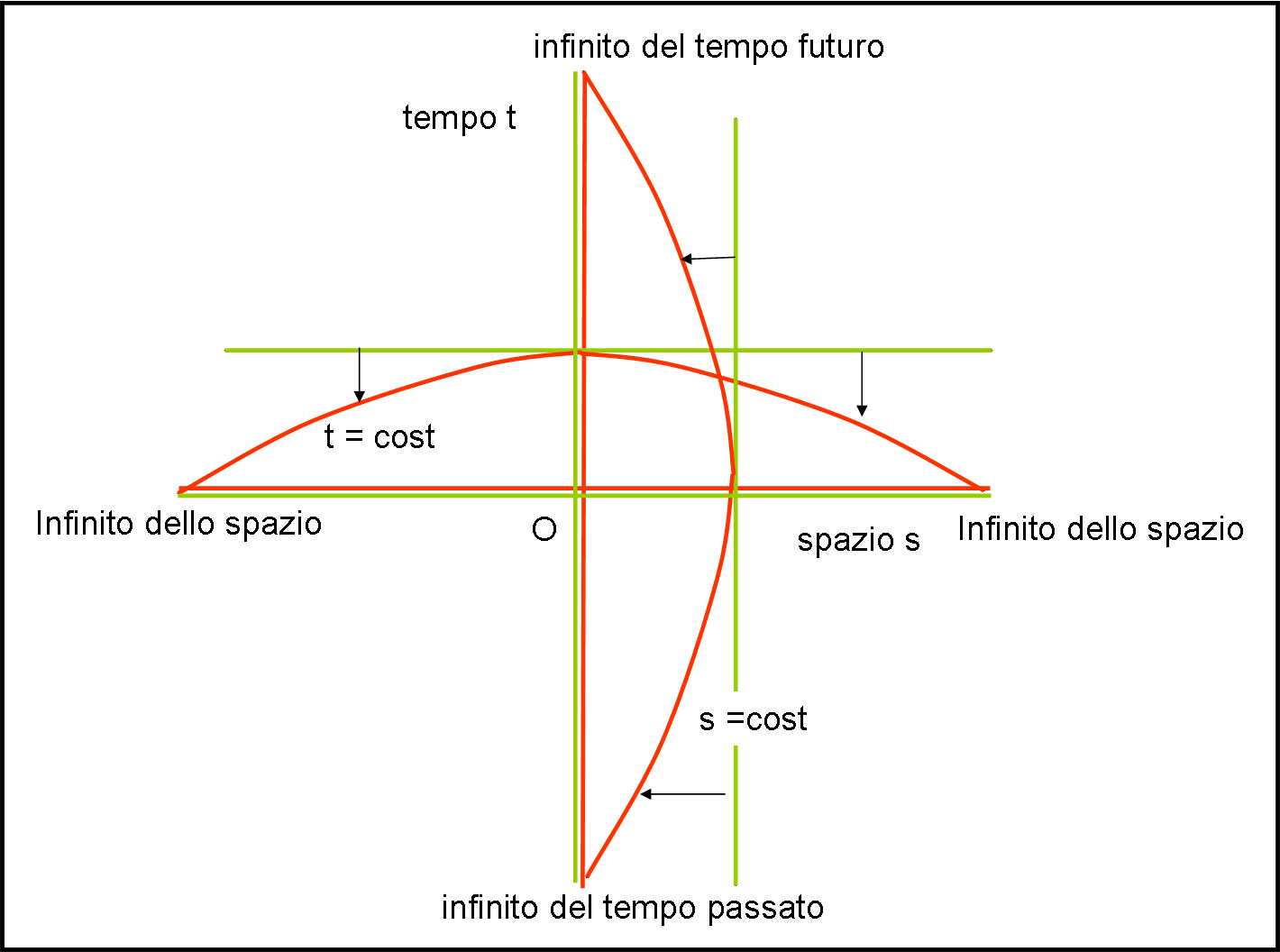
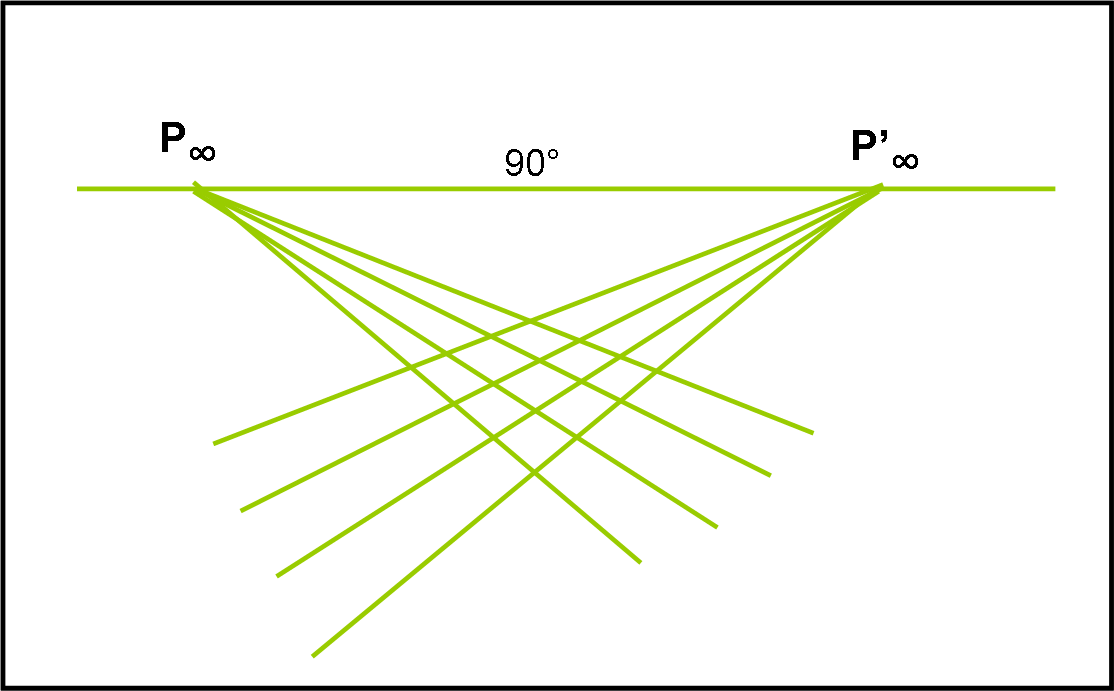
A questo punto possiamo tranquillamente collegare tra loro, in Fig. 10, i punti all’infinito e ottenere un quadrato. I lati del quadrato, dato che uniscono punti all’infinito, sono anch’essi situati all’infinito e rappresentano la linea all'infinito dello spaziotempo (infinito futuro e infinito passato)

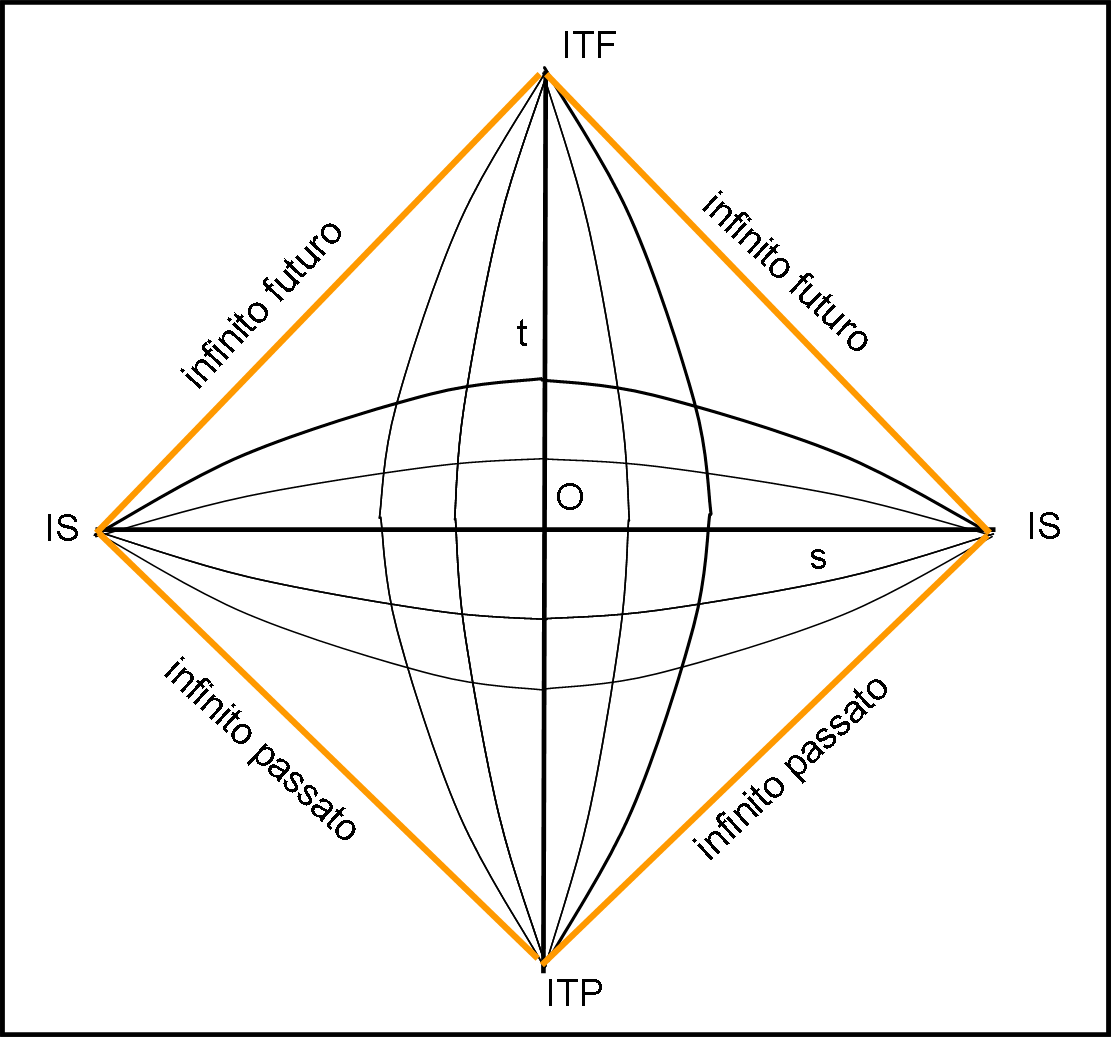
L’effetto più “visibile” di questa operazione è che le linee del passato e del futuro, descrivibili nello spazio a un tempo t, saranno delle curve e non più rette orizzontali parallele come nello spazio-tempo di Minkowski. In altre parole è come se “stringessimo” lo spazio, rappresentando concretamente i suoi punti all’infinito e facendo convergere le rette parallele proprio verso questi punti. Non possiamo stupirci, dato che ogni retta "parallela" deve andare a finire nello stesso punto. Un’analoga operazione possiamo effettuarla per l’asso del tempo. In questo caso le linee descritte da un corpo fermo nello spazio, saranno curve che terminano nei punti all’infinito del passato e del futuro. Esse sono le curve per cui lo spazio s è costante.

Tutto ciò non è altro che lo spaziotempo di Minkowski, dove abbiamo mantenuto la causalità e dove abbiamo sacrificato la conoscenza della lunghezza dei vari segmenti (volendo, però si potrebbero anche ricostruire). Le linee curve orizzontali e verticali non sono altro, ovviamente, che le linee tipo spazio e tipo tempo.

A questo punto, chiediamoci: "Cosa sono mai le linee che uniscono i quattro punti fondamentali?" Ebbene, lo sappiamo bene: la linea dei punti all’infinito. Ma quali sono le linee più famose che partono dall’infinito e terminano all’infinito? Beh… le linee tipo-luce. In poche parole, la retta a 45° rispetto ai due assi che uniscono i quattro vertici è sicuramente una linea tipo-luce e tali e quali sono le rette parallele a lei. Le linee tipo-luce restano delle rette!

Pensiamoci un attimo e scopriamo, subito, che i coni luce si sono mantenuti tali e quali, sempre formati da rette a 45° rispetto alle rette tipo tempo e tipo spazio. La nostra trasformazione è una trasformazione conforme, dato che mantiene gli angoli e lascia le linee tipo luce rettilinee. Per ottenere ciò, non abbiamo fatto altro che stirare e stringere le distanze temporali e spaziali (Fig. 11)

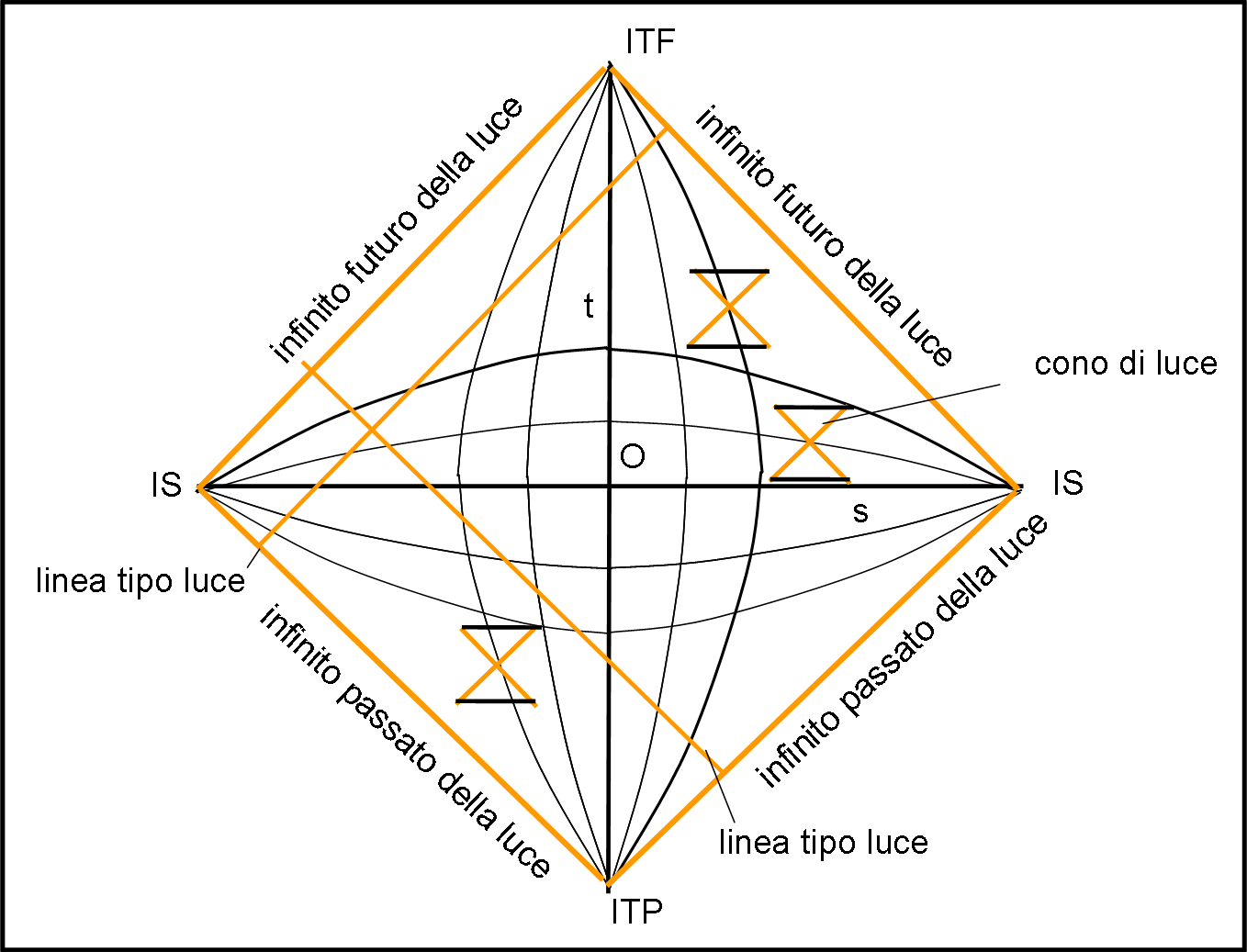
Notiamo, anche, che una geodetica tipo tempo non è altro che un punto che si muove in modo inerziale e la geodetica tipo spazio non è altro che la “comune” retta della geometria di tutti i giorni. Le linee tipo luce , chiamate anche geodetiche nulle, dato che il tempo trascorso su una di queste linee è nullo, non è altro che la traiettoria di un fotone lasciato libero di muoversi.

Diciamo anche che i lati del quadrato possono essere considerati come l’infinito passato e futuro della luce.

Un’idea quasi banale, ma sicuramente geniale.

Il contorno del nostro quadrato rappresenta perfettamente tutto ciò che è infinito nello spaziotempo. Ciò non toglie che si possa lavorare tranquillamente al suo interno, con regole semplici e ben note, come coni di luce non deformati.

Basta considerare un certo evento E e seguire una sua traiettoria percorsa a velocità inferiore a quella della luce. In ogni suo punto possiamo tracciare, come sempre la linea relativa alla luce.

Spieghiamoci meglio…

Come ormai abbiamo capito, le geodetiche tipo tempo cambiano continuamente la loro direzione, passando da un evento a un altro. Preso qualsiasi evento della linea di Universo, si consideri la tangente alla curva nell’evento. Questa tangente deve sempre fare un angolo minore di 45° rispetto alla linea verticale.  E questo deve valere per qualsiasi evento che compone la geodetica tipo tempo (Fig. 12).

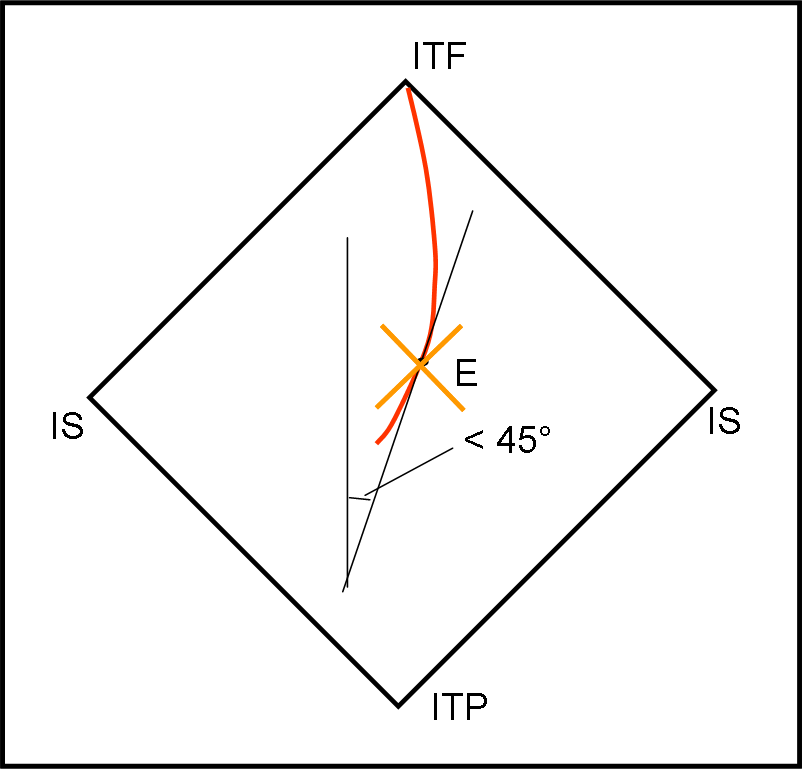
Prima di proseguire, digeriamo bene il diagramma super compatto di Fig. 11 e riassumiamo le sue caratteristiche fondamentali:

1) Il tempo continua a scorrere lungo la verticale e lo spazio a 90° da lui.

2) Le linee tipo luce formano sempre 45° con il tempo e lo spazio. Le linee di Universo (tipo tempo) formano sempre angoli inferiori a 45° con l’asse del tempo. Le linee tipo spazio formano, invece, un angolo maggiore di 45°.

3) Gli stessi intervalli disegnati sulle varie curve non rappresentano distanze o tempi uguali: un centimetro al centro diventa, dopo poco, un chilometro e, addirittura, infinito quando un estremo è infinito.

Disegniamo un buco nero

Non è che io voglia scoraggiarvi, ma la semplicità del diagramma di Penrose è solo apparente. Ricordiamoci che essa ingloba al suo interno la metrica di Schwarzschild. Inoltre, la prima reazione che si ha è quella di aver ottenuto ben poco da questa trasformazione, che mantiene solo le linee tipo luce. In realtà, invece, è più che sufficiente per poter descrivere la struttura causale dell’intero spaziotempo e trattare geometricamente buchi neri, buchi bianchi e orizzonti vari.

Non crediamo, però, che ogni punto della rappresentazione sia davvero un punto, né che una traiettoria sia una vera traiettoria, sia perché stiamo lavorando con uno spazio a una dimensione, sia per la stessa definizione della metrica. Noi cercheremo solo di descrivere i risultati più intuitivi e comprensibili escludendo i calcoli e i concetti decisamente più “pesanti”.

E’ un po’ come se leggessimo Pinocchio con la mente di un bimbo, fermandoci solo sulle avventure rocambolesche e sulla trama esteriore. Menti adulte dovrebbero capire che, dietro quella semplice facciata da favola, vi è una rappresentazione accurata, anche a volte esasperata, della vita reale con tutte le sue miserie, gioie e tristezze. Ecco, cerchiamo, perciò, di rimanere bambini: la lettura adulta è decisamente fuori della nostra portata.

Chi comanda tutto nel diagramma è la luce. Essa ci fa capire cosa può essere raggiunto oppure no nella struttura causale dello spaziotempo. Nella sua versione completa, ogni geodetica parte dall’infinito del tempo passato e termina nell’infinito del tempo futuro. Ogni “punto” di queste geodetiche deformate invia e riceve la luce e poco importa, in fondo, da quale traiettoria sia stata mandata, dato che lei viaggia sempre a 45°.

Tutto ciò che sta all’interno del quadrato, ossia tutti gli eventi di tipo tempo, prima o poi si faranno vedere, basta dargli… tempo.

La loro luce, al limite, ci raggiungerà nel punto all’infinito del tempo futuro. Analogamente, la nostra luce raggiungerà, prima o poi, qualsiasi altro punto all’interno del quadrato, qualsiasi geodetica (traiettoria tipo tempo) percorra. Poco importa la rappresentazione “reale” di queste traiettorie, l’importante è sapere che cosa è legato causalmente a noi (e viceversa). La luce, in queste condizioni, è la migliore maestra.

Evoluzione infinita di una stella 

Per prendere un po’ di dimestichezza con questo tipo di diagramma, disegniamo la storia di una stella qualsiasi, mettendola al centro. Lei nasce nell’infinito passato del tempo e termina nel suo infinito futuro. Poco ci interessa la sua evoluzione fisica… In qualche modo, la sua materia esiste da sempre e cesserà di esistere solo all’infinito. La stella ha certe dimensioni (non c’interessa cambiarle a seconda della sua fase di vita, ma si potrebbe anche fare) che individuano ciò che si vede nella Fig. 13.

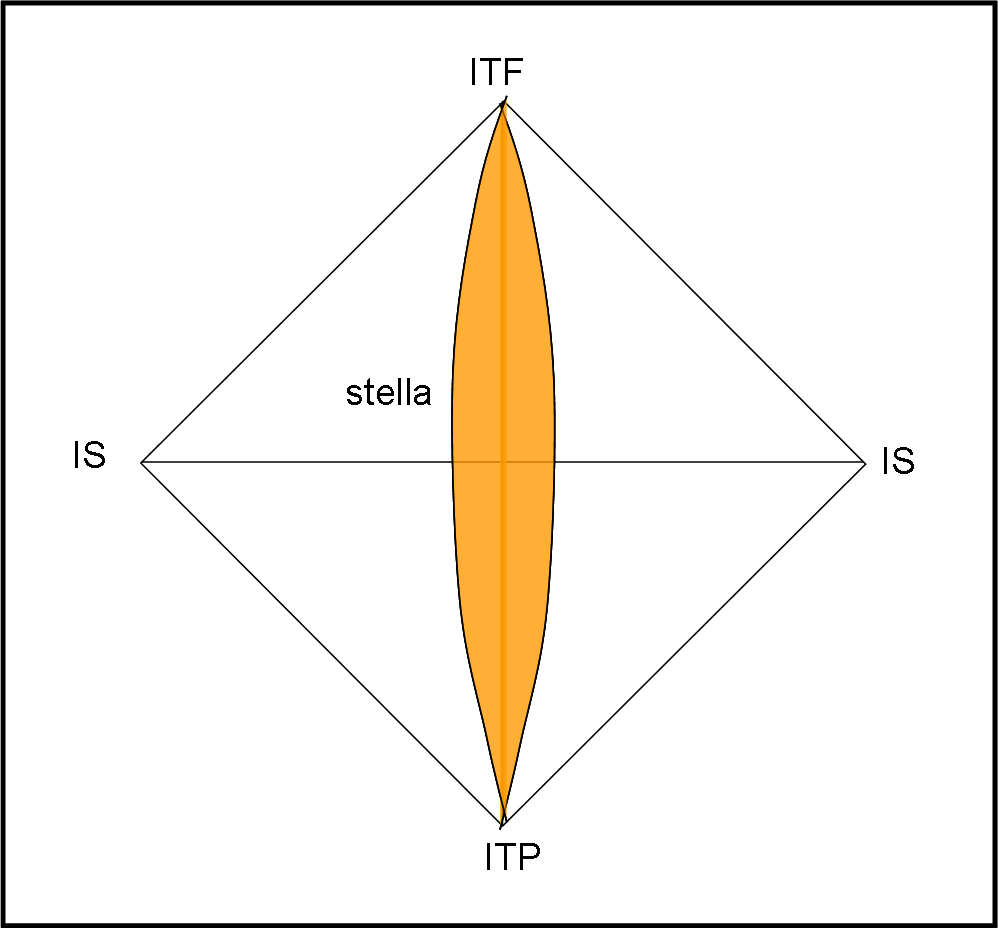
Tanto per non dimenticare, nel diagramma di Minkowski, questa stella teorica sarebbe stata rappresentata da due rette parallele verticali. Se vi dà fastidio immaginare una stella priva di cambiamenti, possiamo anche mettere al suo posto un pianeta o qualsiasi altro corpo più o meno compatto.

Se il nostro oggetto è posto al centro, basta tracciare solo metà del diagramma, ad esempio quello di destra (un triangolo equilatero), dato che contiene tutte le informazioni di cui abbiamo bisogno. Ad esempio (Fig.  14 ), potremmo far partire un raggio di luce da molto lontano (dall’infinito) ed esso incontra la nostra stella o pianeta in un certo istante t della sua esistenza. A quel punto la luce si riflette o viene inviata verso lo spaziotempo e arriverà nuovamente fino all’infinito.

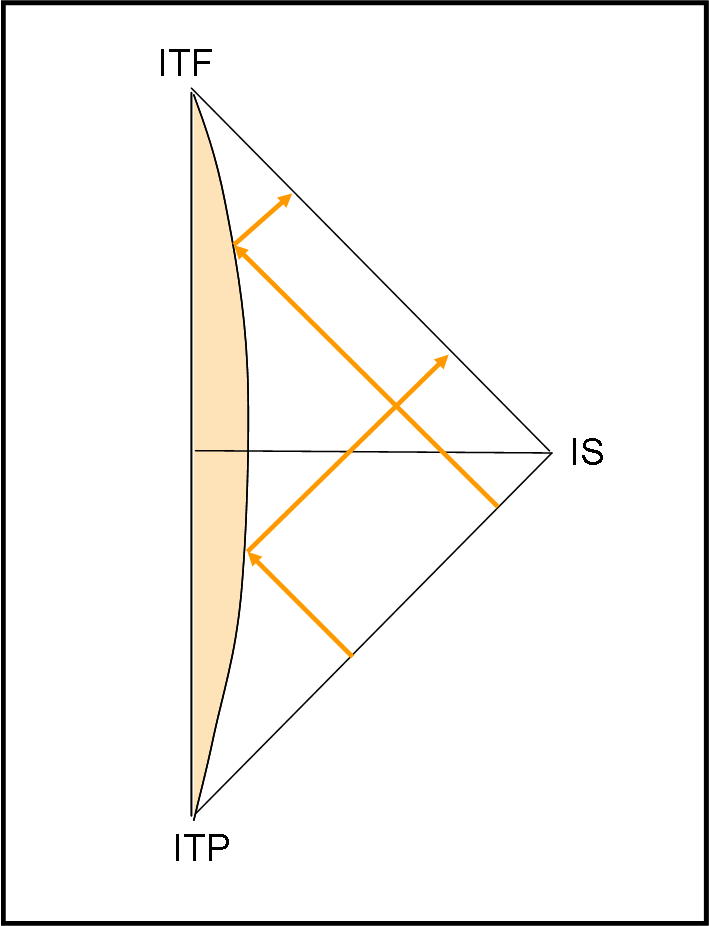
Diciamolo in silenzio… ma tutto ciò sembra di una banalità estrema. L’unica differenza che vediamo rispetto a Minkowski è la possibilità di tracciare raggi di luce che “toccano” l’infinito. D’altra parte, abbiamo il problema di dover disegnare il nostro corpo centrale con due estremi curvilinei che, tuttavia, non comportano un cambiamento delle dimensioni. Le cose, però, cambiano completamente quando la nostra stella ha una massa tale che, dopo aver tentato inutilmente di fermare la sua contrazione, non può che precipitare verso il collasso irrefrenabile fino a scomparire nella singolarità.

Una "strana" singolarità orizzontale

Da quanto sappiamo, trattando con Minkowski, la singolarità sembrerebbe un punto che continua a vivere nel tempo. Tuttavia, questa rappresentazione ha poco senso, in quanto la singolarità capita a un certo istante: dopo non può più essere rappresentata dato che tutti i parametri divergono. Cosa succede, invece, nel diagramma di Penrose? La singolarità diventa un segmento orizzontale, proprio per rispettare il fatto che deve crearsi a un tempo ben determinato. Essa quindi diventa una regione di spazio bloccata a un tempo critico t. In qualche modo, si sta ribaltando lo spazio con il tempo (come si dice solitamente), ma nel diagramma di Penrose questo avviene senza creare salti improvvisi.

Teniamo, comunque, presente che il segmento che corrisponde alla singolarità potrebbe essere considerato il solito punto singolare. In realtà esso è definito come un punto del tempo e tutti gli altri "punti" del segmento non possono certo sopravvivere più a lungo e sono obbligati a fermarsi a quel tempo, diventando, quindi, molto speciali. In altre parole, se il tempo si ferma, anche i punti devono identificarsi in uno solo. D'altra parte se fosse un punto puramente spaziale, dovrebbe continuare a esistere nel tempo, cosa impossibile. Tutto ciò ci porta alla vecchia definizione: una singolarità appare come un muro contro cui si fermano tutte le geodetiche.

In ogni modo, questa rappresentazione non banalissima deriva matematicamente eseguendo la trasformazione di coordinate a partire dalla metrica di Schwarzschild.

Se ci fermassimo adesso, avremmo creato una “singolarità nuda”, raggiungibile senza nessun limite anche se invisibile. No, non preoccupiamoci.  Non è difficile disegnare l’orizzonte degli eventi: esso  è l’ultima linea tipo luce che può essere percorsa prima della caduta inesorabile verso la singolarità. Deve quindi essere un tratto inclinato di 45°, che finisce nell’infinito del tempo futuro, in contemporanea con la singolarità. Il tutto è rappresentato in Fig. 15

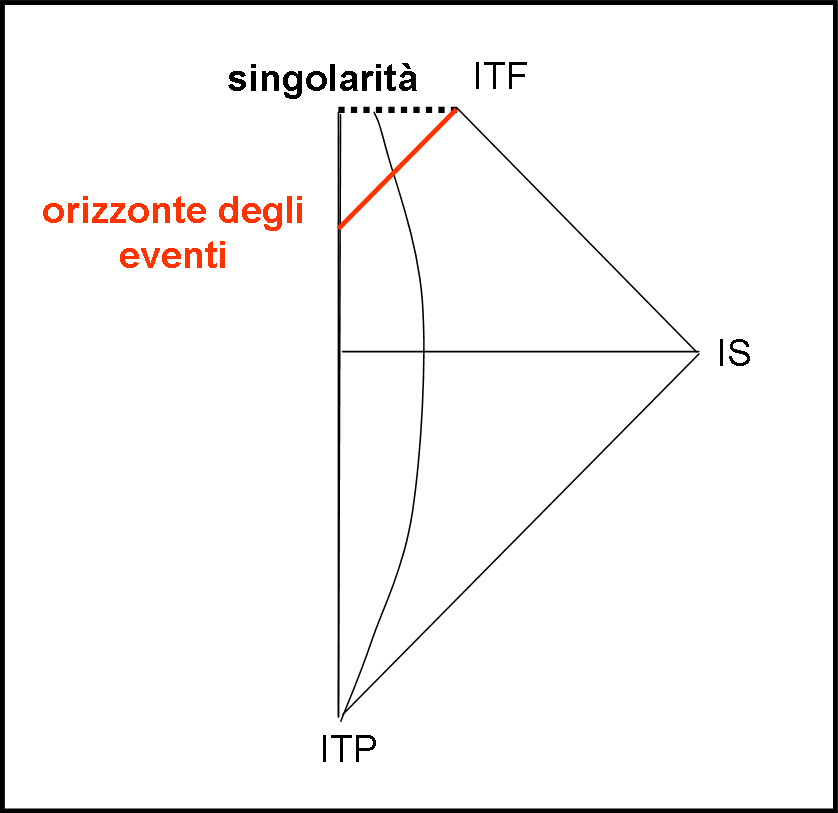
Spieghiamoci meglio. Facciamo uno “zoom” sulla parte più interessante (eliminando anche le dimensioni della stella vera e propria che ormai ha perso di significato nel nostro diagramma) e prendiamo quattro “punti” nel nostro spazio tempo (Fig. 16).

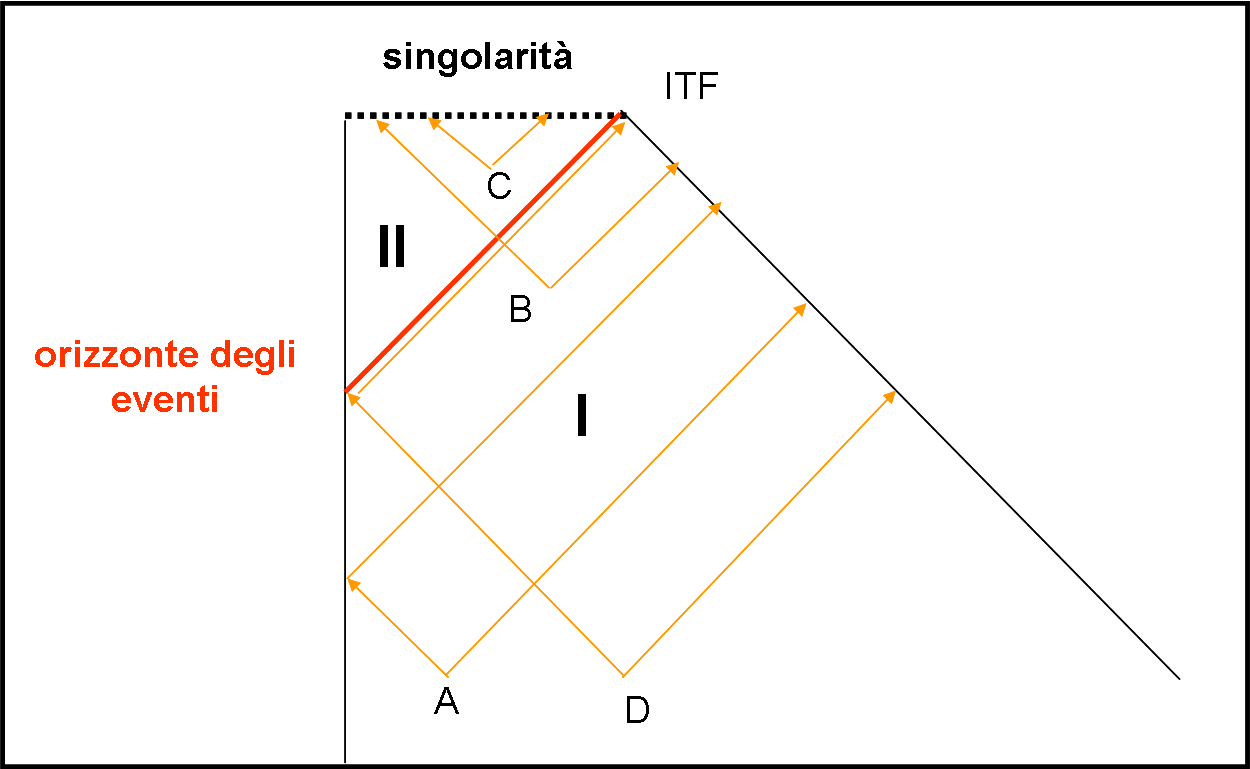
Il punto A manda la sua luce, ma essa non ha alcun problema: o va all’infinito o raggiunge la stella “da giovane” e quest’ultima può liberamente rimandare la sua luce che incontrerà nuovamente la sorgente o terminerà nell’infinito futuro della luce. Il punto B può fare lo stesso per la luce che va a destra ma non per quella che va a sinistra: essa colpisce la stella all’interno della zona proibita e qualsiasi raggio che mandi indietro non potrà che finire nella singolarità. Ancora peggiore è la situazione per il punto C: esso è dentro la prigione senza uscita e i suoi raggi non hanno altra via che finire nella singolarità. Molto interessante è, invece, il punto D. La parte sinistra della sua luce tocca la stella proprio nel punto critico, essa può tornare indietro descrivendo proprio l’orizzonte degli eventi. Ovviamente, essa incontrerà la sorgente iniziale che ha mandato il segnale solo nell’infinito futuro del tempo.

Beh, la nostra idea sul diagramma di Penrose deve essere completamente cambiata. Esso riesce quasi a “nascondere” il ribaltamento dello spazio con il tempo, attraverso la costanza “geometrica” dei coni di luce, ma, soprattutto, divide lo spaziotempo in due zone ben delimitate, la I e la II. La II è proprio relativa all’interno dell’orizzonte, mentre la I è lo spaziotempo “normale”. La zona II è adesso trattabile e analizzabile come se fosse uno spaziotempo normale. Vedremo, in seguito, a cosa può portare uno spaziotempo che, in qualche modo, riesce a descrivere altrettanto bene sia la parte esterna che quella interna all’orizzonte degli eventi.

Prima di fare qualche ulteriore esempio che ci aiuti nel comprendere appieno l’apparente semplicità della rappresentazione, puntualizziamo alcuni concetti che sono stati  introdotti parlando solo di luce. Chi attraversa l’orizzonte degli eventi può vedere la singolarità? Assolutamente no. Essa non può certo inviare la luce verso il passato, ossia da dove sta provenendo il visitatore. Né d’altra parte può mandare luce o informazione verso il futuro. Ecco il vero significato della linea orizzontale. Un qualcosa, però, che dipende essenzialmente dalla divergenza dei parametri fisici. Cosa può succedere realmente dentro e “oltre” la singolarità potrà essere risolto solo e soltanto dalla gravità quantistica: Einstein è costretto a fermarsi come le geodetiche.

Buttiamo lì, anche un altro pensiero… possiamo vedere l’orizzonte degli eventi? No, dato che l’unica sua luce che non cade verso la singolarità è quella che ci raggiungerà nell’infinito del tempo futuro. Sarà però visibile per chi l’ha superato. La sua luce potrebbe, infatti, teoricamente raggiungerlo. Sospendiamo, al momento, queste provocazioni che, magari, sfioreremo più avanti. Una volta di più, però, ci rendiamo conto che i buchi neri “fisici” possono farsi notare solo attraverso ciò che capita nelle loro vicinanze…

Come ripasso e come conferma della perfezione del diagramma, consideriamo, adesso, un pianeta che si avvii, senza problemi, verso il suo infinito (Fig. 17). La sua geodetica non viene intaccata dalla presenza del buco nero. L’astronave A che, a un certo istante, lo lascia e si dirige verso il buco nero può essere disegnata come la linea blu. Essa penetra senza problemi dentro l’orizzonte degli eventi e finisce sulla singolarità. Ricordiamoci che siamo nel sistema di riferimento del buco nero.

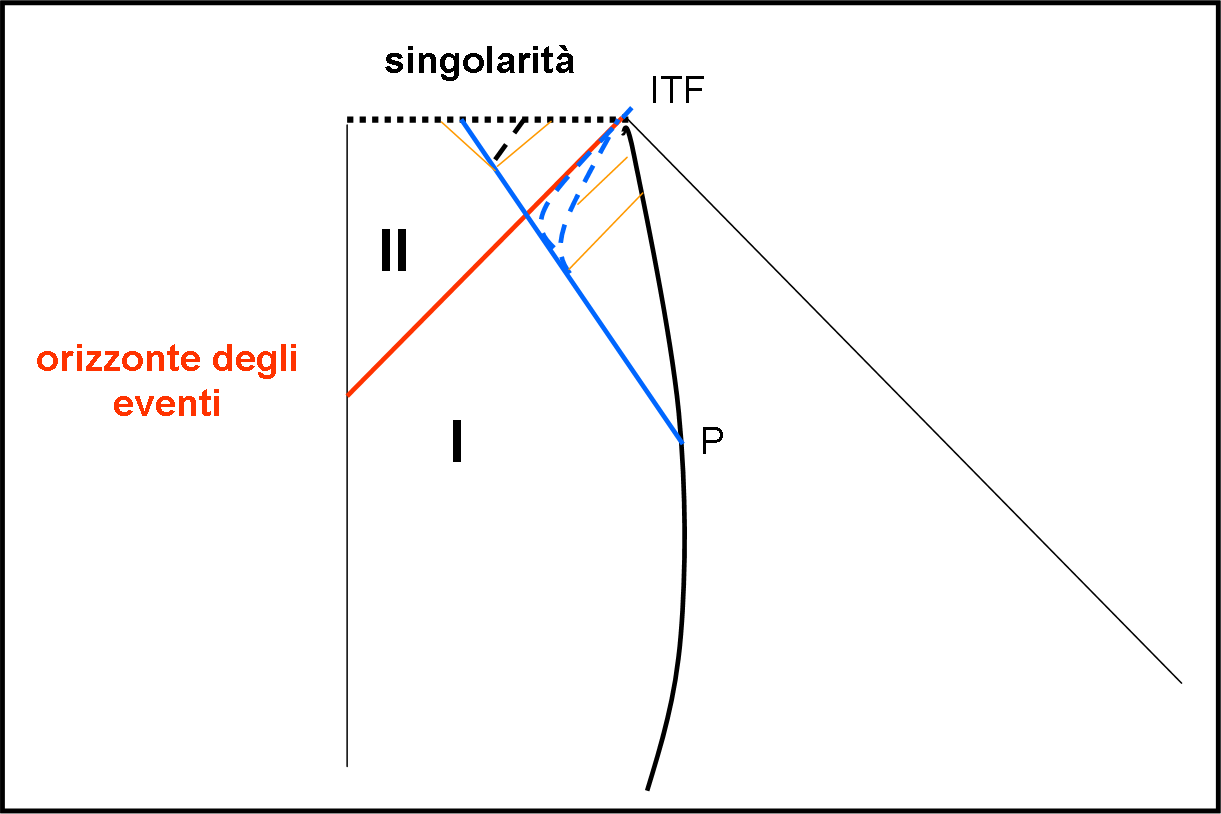
Immaginiamo, dapprima, che all’ultimo momento decida di cambiare rotta. Lo può fare sicuramente se non ha ancora passato l’orizzonte degli eventi. Basterà seguire le rotte indicate dalle curve blu tratteggiate, che lo portano senza grandi problemi al punto all’infinito del tempo futuro. Notiamo come lungo queste traiettorie di salvezza,  un segnale luminoso può essere sempre inviato al pianeta, prima che giunga al punto infinito del tempo. Se, invece, decidesse di tornare indietro, dopo aver passato l’orizzonte degli eventi, le sue fatiche sarebbero sprecate, dato che qualsiasi traiettoria possibile deve stare dentro al cono di luce futuro e quindi lo porterebbe direttamente nella singolarità. Notiamo che, sia dentro che fuori dall’orizzonte degli eventi, abbiamo mantenuto la visione causale delle cose: ogni traiettoria plausibile deve essere contenuta nel cono di luce futuro.

Stiamo attenti a non confondere ciò che stiamo vedendo nelle traiettorie di “salvezza” dell’astronave prima che entri nell’orizzonte, con ciò che vedrebbe il pianeta mentre l’astronave cade nel buco nero. In quel caso eravamo nel sistema di riferimento del pianeta, qui, invece, siamo in quello del buco nero. Le traiettorie tratteggiati sono reali tentativi di fuggire e non un’apparenza dovuta al rallentamento del tempo osservato da P.

Tuttavia, non è difficile capire cosa vedrebbe il pianeta anche in questa raffigurazione. Analizziamo come si comportano i segnali che manda l’astronave  a intervalli cadenzati in Fig. 18.

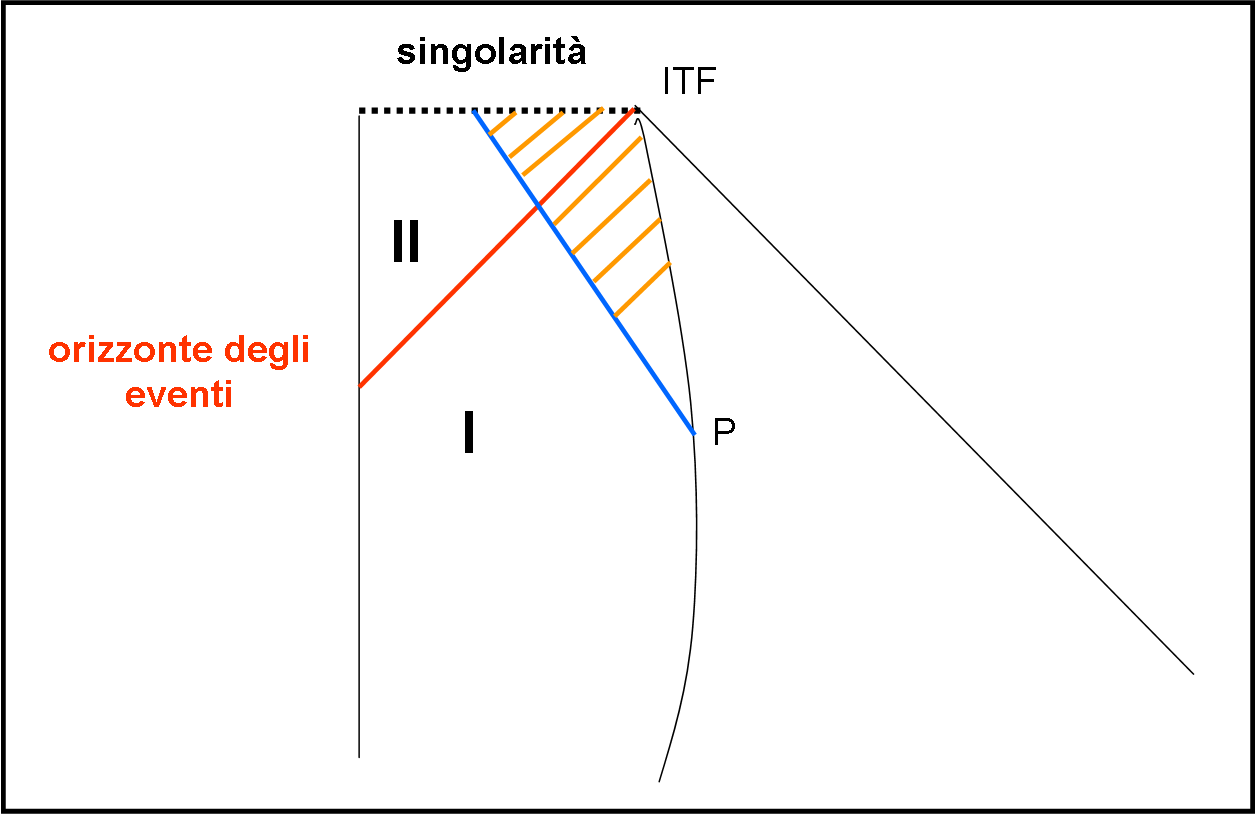
Sappiamo, dal diagramma di Minkowski, che essi arrivano sempre più tardi al pianeta di partenza. E’ questo fatto visibile nella nostra figura? Sicuramente: ogni segnale è una retta a 45° che incontra il pianeta sempre più vicino al punto all’infinito (ricordiamoci che le distanze temporali NON sono mantenute). Il che si traduce in intervalli di tempo sempre più lunghi fino ad essere un intervallo infinito. La nave, per il pianeta, non cadrà mai nel buco nero. L’ultimo segnale luminoso che teoricamente potrebbe ricevere è proprio quello che coincide con l’orizzonte degli eventi e che arriverebbe al punto del tempo infinito. In altre parole, il pianeta deve vivere un tempo infinito per vedere la sua astronave toccare l’orizzonte degli eventi.

L’astronave, nel frattempo, non ha avuto problemi a entrare e a continuare a mandare segnali al pianeta (non si sa mai…). I coni di luce sono sempre orientati nello stesso modo e ugualmente “larghi”, per cui i segnali sono paralleli tra loro e paralleli all’orizzonte degli eventi. Tuttavia, come si vede bene, essi terminano sulla singolarità, un muro invalicabile anche per la luce.

A questo punto tutto diventa un problema tra particelle infinitesime, i soliti nostri eroi quantistici… Cosa faranno? Per adesso “la risposta, amico mio, vola nel vento (stellare)”.

Ci siamo già accorti che qualsiasi difficoltà nel rappresentare ciò che capita fuori e dentro l’orizzonte degli eventi è praticamente sparita. Tutto si può descrivere, praticamente, nello stesso modo, senza singolarità intermedie “apparenti”. Tuttavia, il diagramma di Penrose diventa ancora più utile e interessante, quando si consideri un buco nero nato fin dall’inizio dei tempi…

Ancora sulla "realtà" fisica

Facciamo, ora, una piccola deviazione che può essere abbastanza provocatoria, anche se ci trascina un po’ fuori dal seminato.

Sappiamo che molto probabilmente, noi (come qualsiasi altra cosa) non proveniamo dall’infinito tempo passato. L’Universo è nato dal Big Bang, da una singolarità. Il che vuol dire che tutte le geodetiche (comprese le linee tipo luce) nascono da questa barriera (così come in un buco nero, tutte le geodetiche devono terminare nella singolarità) e non possono proseguire verso un  passato che non esiste o che, perlomeno, non sappiamo trattare fisicamente (chiedendo scusa alle particelle e alla loro meccanica quantistica).

Per ottenere questa situazione possiamo tagliare a metà il nostro quadrato di Penrose e considerare solo l’infinito futuro (a partire dal Big Bang). La Fig. 19 ci mostra cosa succede se noi siamo in T. Siamo riusciti a vedere tutto ciò che proviene da una “parte” del Big Bang. Ciò che rimane del Big Bang  sarà visto in un tempo infinito. Analogamente, noi non siamo ancora stati visti da tutti.

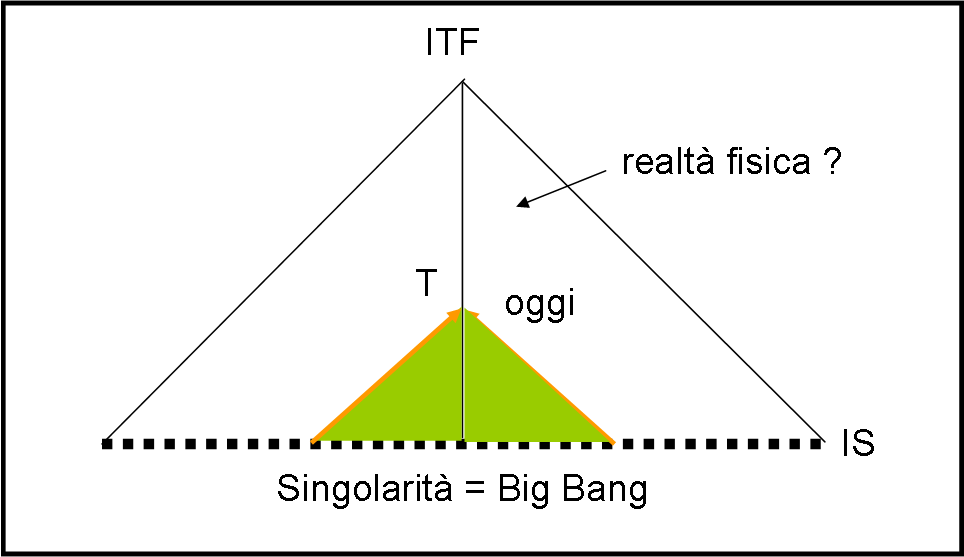
La linea orizzontale è proprio la singolarità (buco bianco?) da cui esce tutta la materia e radiazione, che non possono più tornare indietro. Esso è un vero e proprio muro che non può ricevere niente, ma solo rilasciare; se poi ciò che se ne va è capace di restare “abbracciato” (entangled) a qualcos’altro, è un discorso molto diverso. La singolarità è, ovviamente, una retta dato che corrisponde a un tempo ben determinato, t = 0.

Usando queste coordinate il nostro cono di luce non si può deformare e deve rimanere sempre delimitato da rette  a 45° rispetto all’asse del tempo. Il triangolo verde non è altro che il nostro cono di luce passato. Non ditemi che in questa rappresentazione ultra semplice non si vede l’espansione e/o l’inflazione. Per vedere tutto ciò bisognerebbe passare alle vere traiettorie, ma posso garantirvi che sarebbe possibile.

Abbiamo accennato (non prendetelo come un dato di fatto, ma solo come una similitudine molto azzardata e abbastanza virtuale) al Big Bang come a un buco bianco, con tanto di singolarità. Ma dov’è il suo orizzonte degli eventi? Beh… potremmo dire che non esiste dato che tutto lo spazio tempo non lo incontra mai. In altre parole, il Big Bang è una singolarità “nuda”. Potremmo, però, anche dire (mi si perdoni l’estrapolazione un po’ esagerata) che si riuscirà a incontrare solo nell’infinito futuro, ossia esso sarebbe tutto il triangolo compreso tra le linee dell’infinito futuro della luce. Cosa rappresenti non è difficile a capire e, devo ammettere, che è estremamente simile all’Universo infinito di Giordano Bruno.

Butto giù una frase un po’ provocatoria (che modifica un po' quanto avevo detto tempo fa) : “L’Universo (la realtà globale) è il cono di luce passato di ciò che esisterà al tempo infinito”. Estrapolando ancora… “La nostra realtà dipende da ciò che sarà il futuro ed è quindi inutile cercare di definirla adesso!”. Beh, un modo abbastanza “astuto” per rispondere alla domanda di qualche tempo fa… (QUI).

Fermiamoci qui, per adesso, ricordandoci che il Paese dei Balocchi che stiamo visitando deve restare un mondo di fantasia reale… senza alcun doppio senso. Di più non possiamo fare.

Il diagramma si allarga

Finora abbiamo rappresentato lo spaziotempo “infinito” attraverso il semplice diagramma di Penrose, capace di mantenere ortogonali le linee dei coni di luce, ossia le direzioni della luce che parte, o arriva, da/a una sorgente. Siamo stati anche capaci di evidenziare la singolarità finale e l’orizzonte degli eventi di un buco nero stellare. Lo spaziotempo che lo circonda è descrivibile attraverso la metrica di Karl… ricordiamolo sempre, anche se il tutto sembra un banalissimo disegnino geometrico. In altre parole, la metrica ci permette di definire le traiettorie spaziotemporali (geodetiche) in un intorno del buco nero (o di una massa qualsiasi).

Tuttavia, il diagramma di Penrose, proprio per le sue caratteristiche di simmetria e di semplicità può andare ben oltre e tradurre altre pagine contenute nelle equazioni della relatività generale, un vero e proprio libro dell’Universo, non ancora compreso completamente. Siamo di fronte ad astrazioni, per adesso, che non riproducono situazioni realistiche, ma che impostano un discorso di base della massima generalità.

In particolare, Penrose si occupa di un buco nero “eterno”, ossia un buco nero che è sempre esistito e che sempre esisterà. Esso prende il nome di buco nero completamente esteso di Schwarzschild , che mantiene le limitazioni introdotte dal grande Karl, in particolare quella di non ruotare e di non avere carica.

Riprendiamo in mano l’universo “quadrato” di Penrose e, in presenza di un buco nero eterno, che esiste da sempre, risulta subito ovvio quale sia il suo orizzonte degli eventi futuro: la diagonale superiore sinistra. Essa, infatti, è il luogo dove terminano tutti i raggi di luce e corrisponde perfettamente a ciò che definisce l’orizzonte degli eventi. Oltre quella diagonale si deve trovare il nostro buco nero con la sua singolarità finale, rappresentata da una retta orizzontale, corrispondente a r = 0 nella metrica di Karl. Sul fatto che una linea tipo spazio sia diventata una linea tipo tempo abbiamo già discusso a lungo riguardo alla metrica di Karl. Possiamo, però, fare un’ulteriore esempio terra-terra che aiuti a comprendere meglio questa situazione apparentemente assurda.

A mano a mano che cadiamo verso la vera singolarità, attraversiamo curve con r = cost., ribaltate di 90° rispetto alla posizione che avevano nello spazio-tempo esterno. Immaginiamo, allora, di essere un pesce che si muova alla velocità della luce e che tenti di risalire la corrente di una cascata. Al di fuori dell’orizzonte degli eventi la gravità che lo trascina verso il buco nero può essere controbilanciata, in quanto la velocità di caduta dell’acqua è inferiore alla velocità del pesce. Sull’orizzonte degli eventi le due velocità si equivalgono e il pesce resta immobile (ed è cosi che un osservatore esterno lo vedrebbe per sempre). Una volta superato questo limite, però, per quanto sforzo faccia, il pesce viene trascinato verso il basso, precipitando in una caduta senza possibilità di spostamento se non lungo la verticale. La velocità dello spazio (ossia dell’acqua) ha superato la velocità della luce (ossia del pesce) e lo direzione obbligatoria, trascinando tutto con sé, come nello spaziotempo esterno faceva il tempo. E’ lo spazio che scorre ineluttabilmente e non più il tempo. In altre parole, possiamo dire che la curvatura dello spazio-tempo è diventata infinita.

Torniamo al buco nero eterno…

Il buco nero esiste da sempre, anche nel nostro passato. Come possiamo rappresentare questa situazione? Andiamo avanti con calma e cerchiamo di continuare con le astrazioni senza spaventarci e lasciandoci guidare dalla geometria semplicissima di Penrose. Non dimentichiamo, però, che tutto ciò è descrivibile attraverso equazioni a dir poco spaventose che ci possiamo permettere di non tenere in conto (qualcosa di simile ai diagrammi di Feynman nella QED).

Immaginiamo di avvicinarci all’orizzonte degli eventi futuro (quello più facilmente intuibile) lungo la traiettoria verde della Fig. 20.

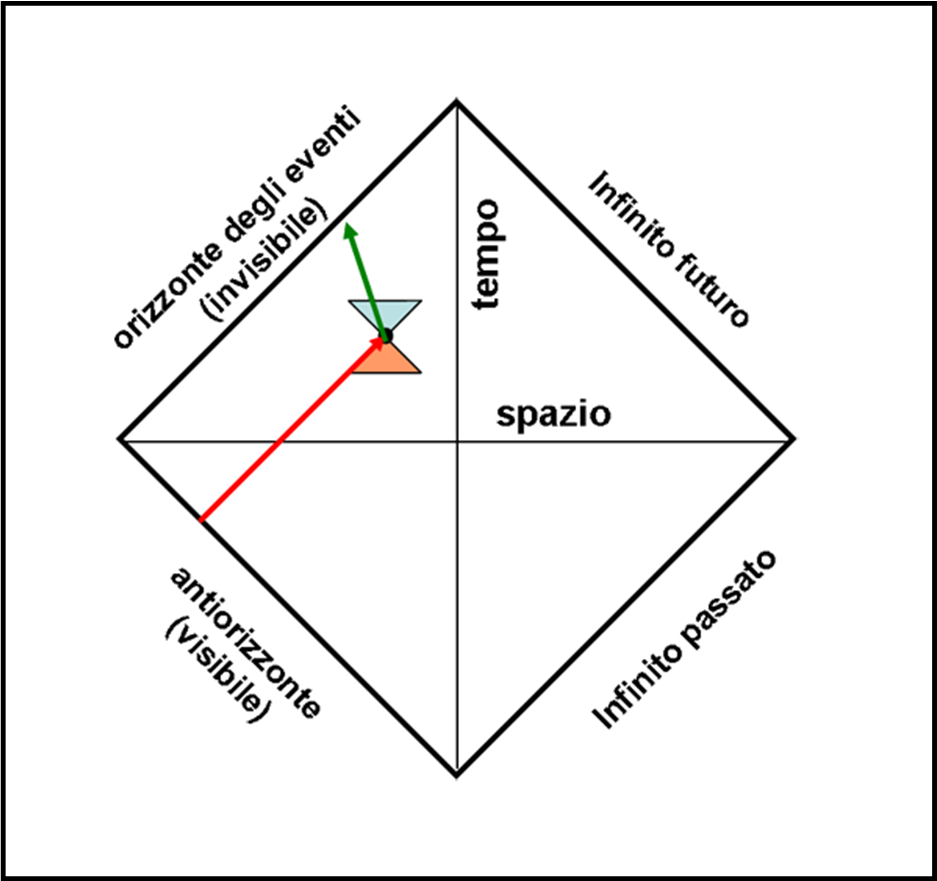
Non dobbiamo deformare niente, in quanto sappiamo bene che il diagramma di Penrose lascia immutati i coni di luce. Riusciamo a vedere l’orizzonte degli eventi? Intuitivamente diremmo forse di sì. E’ lì davanti a noi con tutta la materia che vi sta precipitando. Se non lo vediamo praticamente, ne intuiamo, comunque, la posizione. Ebbene NO. Niente di più sbagliato.

Noi non possiamo vedere l’orizzonte degli eventi, perché la sua luce non può assolutamente raggiungerci. Per farlo dovrebbe muoversi verso il passato, ma sappiamo bene che il tempo viaggia solo verso il futuro. Ricordiamoci che tutto ciò che riusciamo a vedere vicino a un buco nero fa parte dei fortunati fuggitivi, capaci di deviare la loro traiettoria all’ultimo momento e tornare nel mondo … reale.

Ma, allora, cos’è che vediamo? Vediamo un orizzonte degli eventi immaginario che diventerà, però, estremamente interessante tra poco. E’ una specie di illusione ottica: noi pensiamo di vedere il lato sinistro in alto del quadrato e invece ciò che vediamo è il lato sinistro in basso, quello che rappresenta l’infinito passato della luce. In realtà, è ovvio: solo lui può averci inviato la luce che ci sta raggiungendo. Esso, proprio perché è quello che si rende visibile e che ci inganna sulla reale posizione dell’orizzonte degli eventi, prende il nome di antiorizzonte. Possiamo anche chiamarlo orizzonte passato del buco nero. Tuttavia, non possiamo dimenticarci delle caratteristiche di questo orizzonte così strano… da lui esce tutta la luce che proviene dal passato (proprio il contrario di quanto abbiamo sempre pensato attorno ai buchi neri).

Non è certo difficile allungare l’orizzonte passato e determinare, in Fig. 21, un triangolo, delimitato dall’estensione dell’orizzonte passato, dall’orizzonte futuro e dalla singolarità. Questo non è altro che il nostro buco nero.

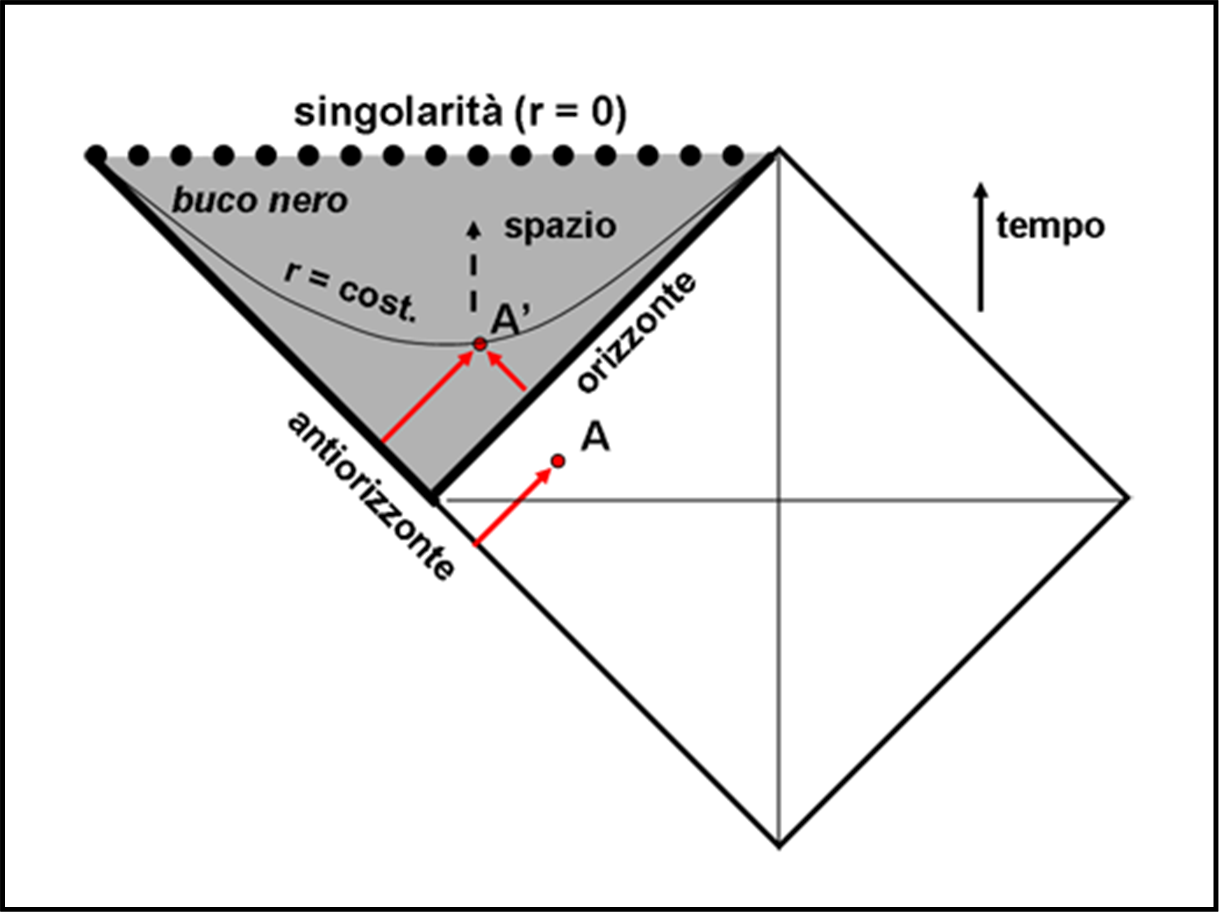
Notiamo subito che l’estensione dell’orizzonte passato diventa orizzonte degli eventi futuro per un “qualcosa” che sta alla sua sinistra. Ci torneremo tra poco, per adesso entriamo dentro l’orizzonte degli eventi futuro, quello più “gestibile”. Al suo interno sappiamo come muoverci, dato che ce lo indica chiaramente la metrica di Karl. A parte mille e una stranezza, capita un qualcosa di veramente inaspettato: si riescono a vedere due orizzonti, sia quello futuro che quello passato. Ormai, infatti, la luce può raggiungerci sia da destra che da sinistra. Ci accorgeremmo di vedere doppio (sempre che ci riuscissimo, ovviamente): vedremmo l’orizzonte sdoppiarsi, in quanto oltre quello reale continuerebbe a essere visibile anche l’antiorizzonte.

Il viaggio si è concluso? In questo caso particolare (buco nero statico) il nostro destino è segnato. Il diagramma di Penrose può, però, mostrarci molto di più e, magari, darci una speranza. La figura, infatti, può ancora svilupparsi.

Universo parallelo

Non è certo difficile prolungare qualche linea e ripetere le considerazioni precedenti. Quello che otterremmo è la Fig. 22.

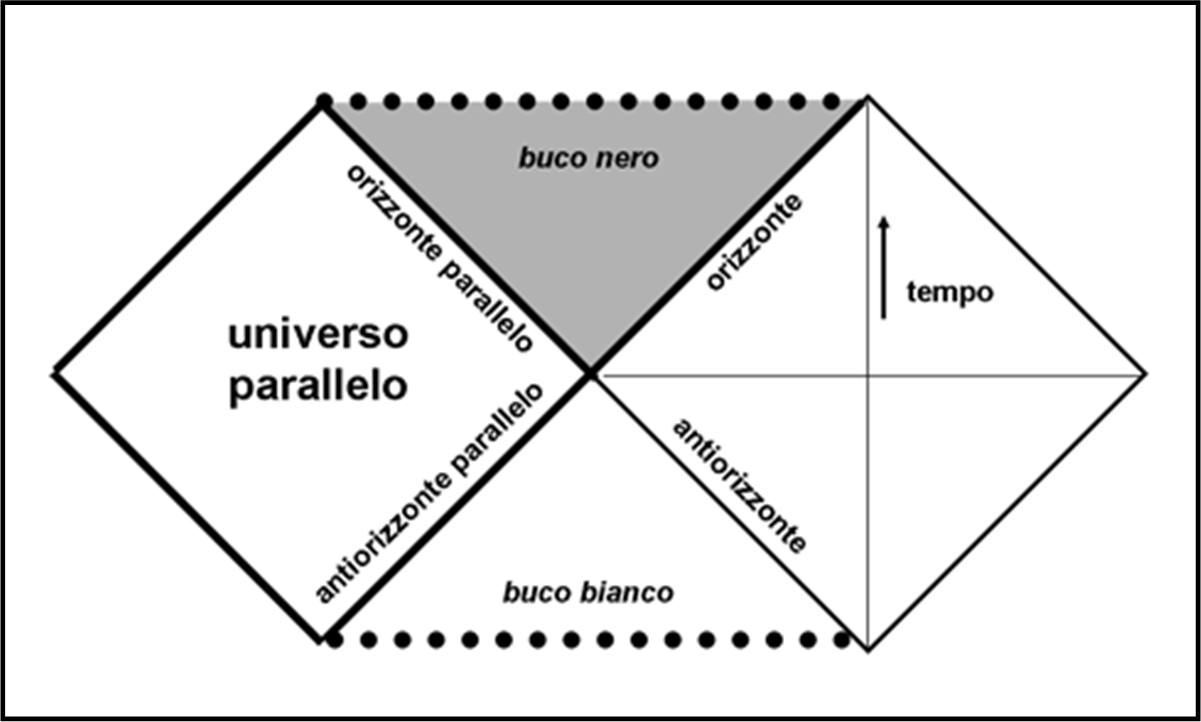
Simmetricamente al triangolo del buco nero, si può facilmente costruire un triangolo uguale e opposto. Anch’esso contiene una singolarità, ma essa ha una caratteristica inversa: da lei si può solo scappare (la direzione della cascata è invertita). Un oggetto posto al suo interno verrebbe espulso verso il nostro Universo attraverso l’antiorizzonte. Insomma, altri non è che un buco bianco. Ricordando quanto detto precedentemente, questa singolarità è del tutto nuda, dato che niente vieta il passaggio verso lo spaziotempo piatto.

Non solo però… Si può anche costruire un quadrato uguale a quello che ha dato il via al diagramma: un Universo parallelo, con le stesse caratteristiche del nostro, ma irraggiungibile. Perché irraggiungibile? Basterebbe riuscire a entrare dentro al buco bianco e potremmo essere cacciati fuori nell’altro Universo. Purtroppo no. Per entrare nel buco bianco dovremmo viaggiare verso il passato. Sfortunatamente, la cosa ci è vietata. Analoghe condizioni sarebbero valide per gli abitanti dell’Universo parallelo. E pensare che i due “buchi” hanno un punto in comune, un passaggio segreto, ma non praticabile (nelle nostre ipotesi).

Il diagramma di Penrose applicato a un buco nero statico ammette e descrive benissimo i buchi bianchi e gli Universi paralleli, ma non lascia speranze di contatti “alieni” tra Universi. Noi non potremmo raggiungere i nostri amici e nemmeno potremmo vederne sbucare qualcuno da un buco bianco, in quanto non ci sarebbero potuti entrare.

Incontri momentanei

No, non siate così tristi. Molte cose possono essere ottenute… basta non avere paura. Immaginiamo un esploratore terrestre A1 e uno A2 del pianeta Terra2, dell’altro Universo, che non temano l’ingresso in buco nero. Essi, prima della fine o, almeno, prima dell’incontro misterioso con la singolarità, avrebbero modo di conoscersi.

Non è difficile descrivere le traiettorie dei nostri avventurosi astronauti (Fig. 23). I due pianeti Terra e Terra2 seguono le loro linee di Universo, mentre le due astronavi valicano i loro orizzonti degli eventi futuri e possono incontrasi prima di cadere dentro la singolarità.

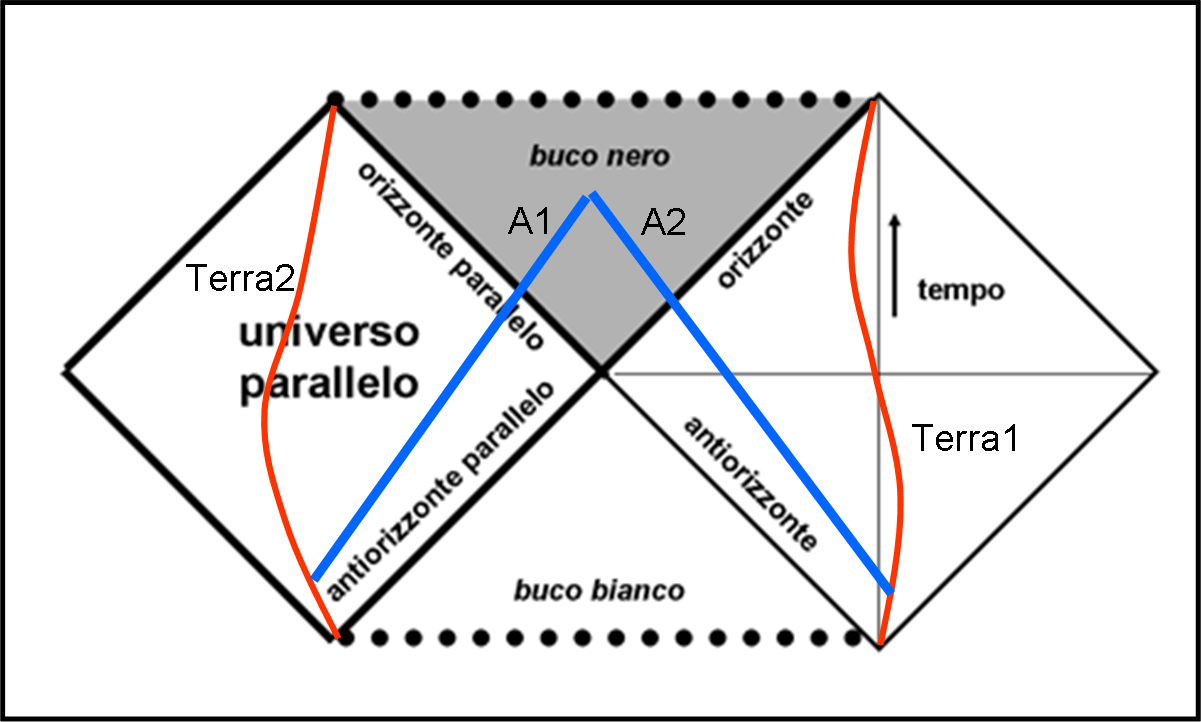
Vale, però, anche il contrario (Fig. 24)… due astronauti caduti in un buco bianco (non chiedetemi come!) o nati al suo interno (magari era uno solo che si è sdoppiato... ), possono tranquillamente uscire attraverso l’orizzonte passato e andare a vivere in due universi diversi.

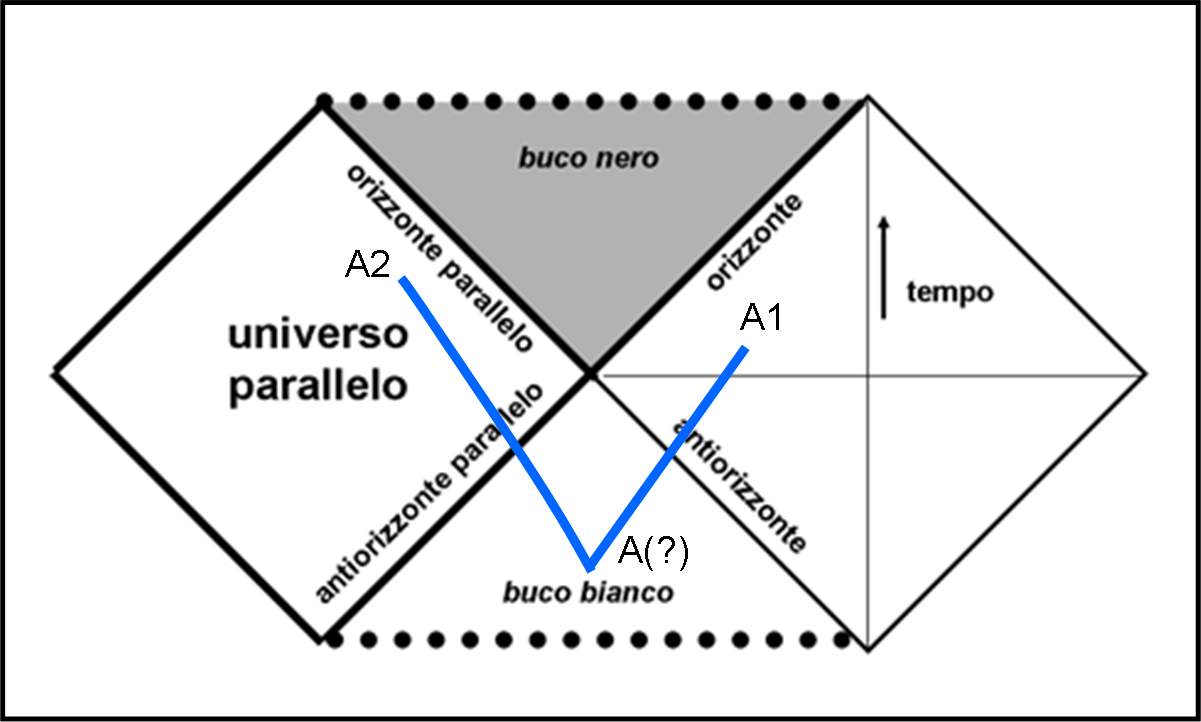
Potrebbero anche ricordarsi del loro passato in cui erano molto amici. Talmente amici che ognuno faceva esattamente quello che faceva il compagno. Nei rispettivi universi in cui sono usciti questa memoria potrebbe rimanere per sempre. Se questa possibilità non ricorda, in qualche modo, l’entanglement delle particelle quantistiche, prendetemi pure a sassate! Non andiamo oltre, ma riflettiamo, ancora una volta, su quanto sia davvero fondamentale riuscire a descrivere una relatività quantistica (tra poco ci torneremo sopra).

Altre possibilità di viaggio sono escluse, dato che implicherebbero il superamento della velocità della luce e questo è impossibile.

Il diagramma di Penrose applicato a un buco nero statico ammette e descrive benissimo i buchi bianchi e gli Universi paralleli, ma non lascia speranze di contatti “alieni” tra Universi. Noi non potremmo raggiungere i nostri amici a casa loro e nemmeno potremmo vederne sbucare qualcuno da un buco bianco, in quanto non ci sarebbero potuti entrare. Che peccato! Riusciamo a vedere il loro confine (l’antiorizzonte) che ci ha ingannato facendosi passare per orizzonte degli eventi, ma mai potremo vedere uscire qualcosa da lui.

Wormhole

Vi è, però, un punto molto particolare in questo scenario fantastico: il punto di contatto tra due Universi paralleli.

Esso si trova attraverso le equazioni di Einstein, tanto per cambiare, e prende il nome di ponte di Einstein-Rosen. Un passaggio puramente teorico, ricavabile attraverso la metrica di Karl applicata al buco nero eterno, che non scongiura, però, il fatto che per attraversarlo in qualche modo bisognerebbe sempre superare la velocità della luce.

Per dare solo una vaga idea pensiamo allo spaziotempo di Karl che rappresenta la situazione a mano a mano che ci si avvicina alla singolarità (diagramma embedding). Considerando anche valori negativi delle radici quadrate si ottiene un imbuto alla rovescia perfettamente simmetrico a quello che già conosciamo (Fig. 25), ossia un buco bianco.

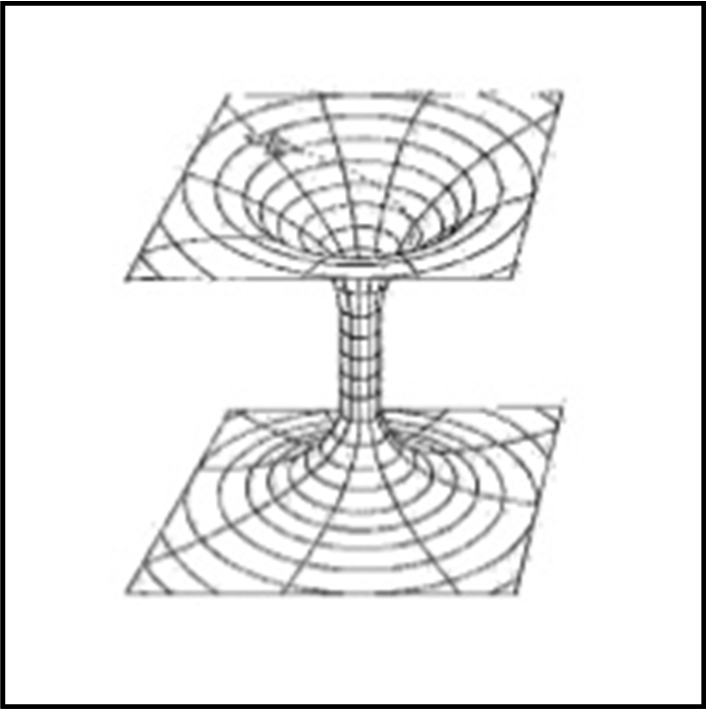
La sfera di dimensioni decrescenti che dà luogo ai vari cerchi del diagramma embedding non diventa mai veramente un punto e questo fatto implica una specie di tunnel che permetterebbe il passaggio tra i due universi (Fig. 26). Il passaggio ci sarebbe, ma andrebbe comunque superato andando più veloci della luce.

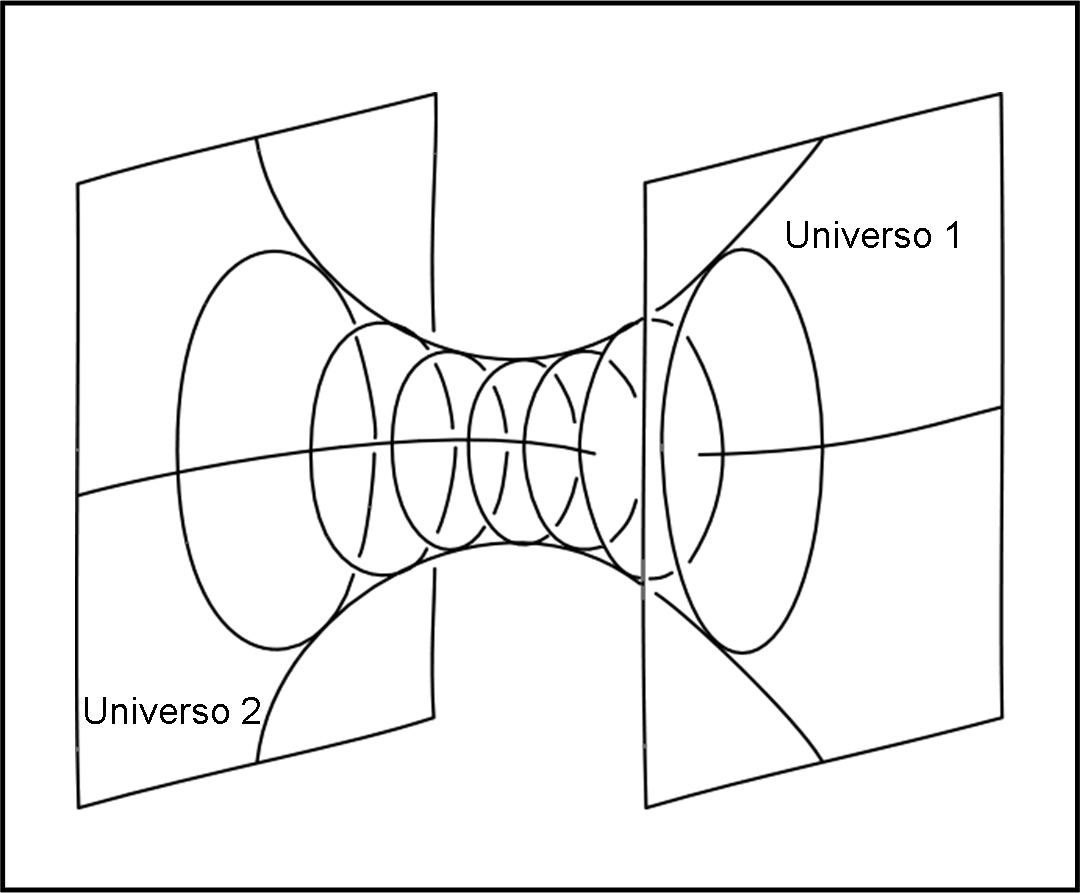
Un ponte che nessuno pretendeva potesse essere reale per il macrocosmo, ma per un qualcosa confinato nel microcosmo: un ponte di Einstein-Rosen rappresentato da un elettrone inteso come foro spaziotemporale in cui convergono linee di forza elettriche. Volando con la fantasia il nostro imbuto non potrebbe rappresentare due particelle entangled? Esse sarebbero separate dal meccanismo dell’entanglement così come i due Universi sarebbero separati dal ponte di Einstein-Rosen.  Questi “ponti”, chiamati anche wormhole (buco del verme) sono ipotetiche vie di passaggio dello spaziotempo che possono abbreviare enormemente la vera distanza tra due eventi.  L’ Entanglement non è altro che un’altra via per connettere due oggetti molto distanti tra loro, che continuano a essere collegati (Fig. 27).

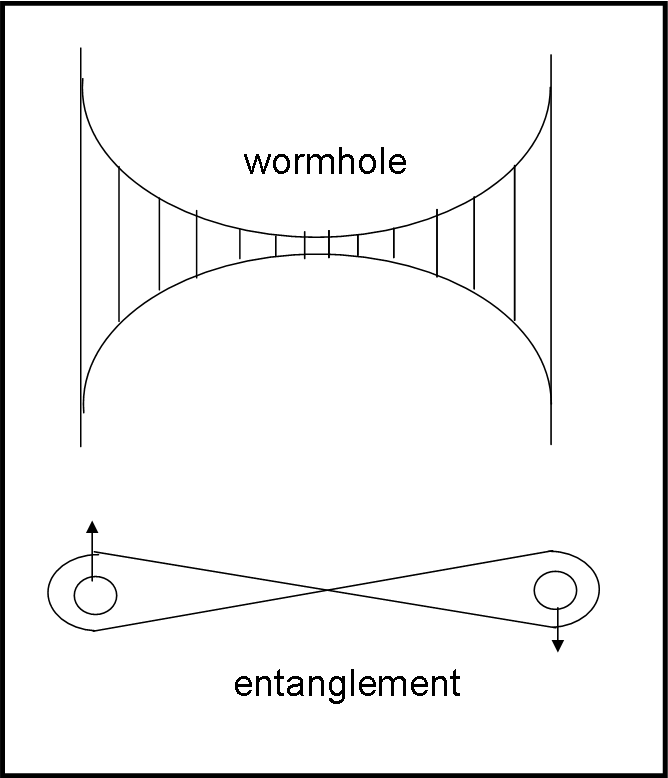
Mentre il secondo meccanismo è stato dimostrato, il ponte non lo è ancora stato. Forse, tutto si risolverebbe applicando la tanto ricercata relatività quantistica. Oppure, potrebbe darsi che certi “passaggi” restino aperti solo per sistemi isolati e non per strutture troppo complesse. Basta, basta! Altrimenti la testa comincia a girare.

Conclusioni

A proposito di giramenti e/o di rotazioni, considerando buchi neri rotanti e/o carichi, la situazione evolve in modo ancora più stupefacente (insieme alla matematica che li descrive) e il diagramma di Penrose si allarga sia sopra che sotto, permettendo teoricamente di passare da un buco nero a uno bianco e visitare altri Universi. Tuttavia, non è cosa per noi, anche se tutto ciò è scritto nel libro di Einstein e, quindi, un giorno chissà…

Non voglio, infine, discutere della radiazione di Hawking. Essa sembrerebbe permettere l’uscita di qualcosa da un buco nero. Tuttavia, è una visione molto ambigua… In realtà, niente esce dal buco nero, ma potrebbe capitare che una particella riesca a sfuggire prima di entrare, mentre la sua antiparticella no. Si avrebbe, quindi, una perdita di energia o qualcosa del genere, ma non una vera uscita di materia. La teoria è ancora troppo poco affiancata da osservazioni reali e preferisco lasciarla tra quelle fantascientifiche. Il problema della perdita di informazione resta aperto e senza l’aiuto delle particelle quantistiche rimane qualcosa di insolubile.

Un commento molto generale (che probabilmente ripeterò in altri articoli…)

Voglio ricordare cosa diceva Einstein riguardo all’etere. In qualche modo troviamo un collegamento con i nostri articoli sulla velocità della luce e questi sui buchi neri. Egli, in fondo, credeva nell’etere e, benché la sua teoria della RR nasce proprio dall’annullamento di questa sostanza misteriosa, continuava a pensare che, in fondo, il suo spaziotempo, capace di curvarsi, di reagire e partecipare alle azioni fisiche, poteva proprio prendere il posto dell’etere. Uno spaziotempo quasi “materiale”. All’opposto, egli era dubbioso sulla reale contrazione delle lunghezze, ma, alla fine, il suo spaziotempo così attivo poteva realmente reagire a un oggetto in moto e contrarlo, come proposto da Lorentz. Niente da fare, cari amici, quanto un effetto sia fisicamente reale (sempre che si capisca cosa sia realmente reale) rimane un problema aperto.

Nuovamente, basterebbe considerare il vuoto teorico come un “non vuoto”, abitato da una popolazione incredibile di particelle (o di energia, come preferite) che lo rendano nuovamente simile a una specie di etere. Folletti che nascono e scompaiono in un tempo immisurabile. Forse, per capire quanto siano reali le conseguente della RR e della RG, bisognerebbe veramente capire il linguaggio forbito e perfetto di questo microcosmo, ancora quasi del tutto incompreso. Ci vorrebbe una pietra di Rosetta per la relatività quantistica.

Feynman, con la sua visione giocosa e senza freni dei rapporti tra fotoni ed elettroni (energia e materia) aveva forse intuito la strada, ma, al momento nessuno è in grado di seguirla. Spariamo che tra i giovani lettori del nostro Circolo ci sia proprio questa mente abbastanza infantile da credere alle favole e abbastanza matura per dedurne la morale più nascosta. La speranza, anche nel mondo di facebook, è l’ultima a morire!

 

NEWS del 10/4/2019 - Ottenuta la prima prova visiva diretta di un buco nero!