Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo

 

Dopo la favoletta della volta scorsa, non ci rimane che spiegare l’esperimento di Michelson e Morley in maniera un po’ più scientifica, utilizzando (poca) matematica e geometria.

Qualche considerazione preliminare

Non sono pochi quelli che credono che il Nobel sia stato dato all’esperimento e alle sue conclusioni, trovando ciò poco onesto, in quanto il risultato è stato, in realtà, un completo fallimento. A parte il fatto che dimostrare che non c’è bisogno di etere per trasportare le onde elettromagnetiche sarebbe già un risultato non da poco, il Nobel è stato dato SOLO a Michelson (e non a Morley che aveva collaborato alla pari nell’esperimento, portando migliorie decisive) per il metodo che aveva ideato. Utilizzare il fenomeno dell’interferenza luminosa (QUI e QUI) per misurare differenze di percorso (meglio dire “cammino ottico”) o di tempo, ben al di sotto delle possibilità degli strumenti tradizionali, ha aperto le porte a una tecnologia eccezionale, che ancora oggi viene usata in mille e una situazione. Nobel all’interferometro, perciò, e non alla scomparsa dell’etere.

Un minimo di storia

La teoria ondulatoria della luce è generalmente fatta risalire a Huygens, tra il 1678 e il 1690. Egli non poteva che assumere un’analogia fra la luce e il suono e, quindi, non poteva fare altro che pensare all’esistenza di una certa “materia” tra la sorgente della luce e l’osservatore. Non potendo certo essere lo spostamento della materia a trasportare la luce, essa, come il suono, doveva consistere in oscillazioni che si propagavano in un mezzo materiale. Nel 1802 Young ipotizzò “un etere luminifero, rarefatto ed elastico: tutte le volte che un corpo emette luce, vengono eccitate delle onde nell’etere”.

Nacque così il concetto di un etere trasportatore della luce, simile a un fluido rarefatto, elastico, senza peso, presente in tutto l'Universo. Nel 1804, ancora Young sosteneva: “... Sono disposto a credere che l'etere luminifero pervada la sostanza di tutti i corpi materiali, con resistenza piccola o nulla, forse liberamente, come il vento passa attraverso un boschetto di alberi …”

Nel frattempo, il genio di Maxwell operava la sintesi dell’elettromagnetismo, dimostrando che sia le azioni elettriche che quelle magnetiche si propagavano come onde di velocità uguale a quella della luce visibile, che ne era, quindi, un caso del tutto particolare.

L'etere diventava così la base fondamentale per le azioni elettriche e magnetiche. Qualunque cosa fosse, doveva pervadere tutto lo spazio. Lo stesso Maxwell nel 1878 scriveva: Qualunque difficoltà possiamo avere nel formare un'idea consistente della costituzione dell'etere, non ci può essere dubbio che gli spazi interplanetari e interstellari non siano vuoti, ma siano occupati da una sostanza materiale o corpo, che è certamente il più grande e probabilmente il corpo più uniforme fra quelli di cui abbiamo qualche conoscenza.”

Ma l’etere era fermo o si muoveva? Diverse erano le ipotesi… secondo alcuni, i corpi celesti potevano trascinare l'etere con sé nel loro moto in prossimità della superficie (come una specie di atmosfera). Secondo altri lo potevano fare, parzialmente, solo corpi dotati di particolari proprietà ottiche (come quelli trasparenti). Oppure, come diceva Lorentz, l'etere era a riposo. In quest'ultima ipotesi, la velocità della luce che era c rispetto all'etere, rispetto a un altro corpo in moto con velocità v nell'etere, doveva essere c +/- v, con grande soddisfazione di Galileo Galilei.

Esperimenti condotti sulla Terra con sorgenti di luce terrestri avrebbero dovuto mettere in evidenza tale cambiamento di velocità. Questo fatto equivaleva ad ammettere che, almeno per i fenomeni elettromagnetici e ottici, l'etere costituiva un riferimento assoluto. La velocità della luce con sorgenti terrestri fu proprio determinata in questo modo, utilizzando esperimenti in cui la luce percorreva una certa distanza sia in un verso che nell’altro (li vedremo tra non molto in un altro articolo sulla misura della velocità della luce). Lo stesso percorso rettilineo eseguito all’andata e al ritorno permetteva di fare la media, trascurando i termini di secondo grado in v/c.

Infatti, se d è la lunghezza del percorso, si ha che il tempo totale, tra andata e ritorno, vale:

t = d/(c + v) + d/(c – v) = d(1/(c + v) + 1/(c – v)) = d(c + v + c – v)/(c² – v²)

t = 2d c/(c² – v²)

Misurato il tempo, basta dividere la lunghezza totale del percorso (andata e ritorno) per il tempo percorso e si ottiene la velocità della luce a meno di un fattore del second’ordine in v/c, che può essere trascurato:

2d/t = c/(c² – v²) = c (1 – v²/c²) ≈ c

Maxwell osservava: “Se fosse possibile determinare la velocità della luce, osservando il tempo che impiega per viaggiare tra una stazione e un'altra sulla superficie della Terra, potremmo, confrontando le velocità osservate in direzioni opposte, determinare la velocità dell'etere rispetto a queste stazioni terrestri. Però tutti i metodi con cui è possibile determinare la velocità della luce da esperimenti terrestri dipendono dalla misura del tempo richiesto per il doppio cammino da una stazione all'altra e ritorno, e l'aumento di questo tempo .... sarebbe non rilevabile”.  In poche parole, bisognava essere in grado di evidenziare grandezze dell’ordine di (v/c)².

Questo è stato il problema che Michelson decise di affrontare nel 1881 (in modo troppo “rozzo”) e nel 1887 insieme a Morley.  Doveva evidenziare la differenza di velocità della luce dovuta al moto della Terra attraverso l'etere, cioè provare sperimentalmente l'ipotesi dell'etere a riposo, data per certa la sua esistenza.  Per far ciò, come già detto, doveva usare un metodo sensibile a una variazione del secondo ordine di v/c. E questo metodo non poteva basarsi certo su misure dirette.

Nel 1881 disse: “La teoria ondulatoria della luce assume l'esistenza di un mezzo chiamato etere, le cui vibrazioni producono i fenomeni della luce, e che è supposto riempire tutto lo spazio… Assumendo che l'etere è a riposo, mentre la Terra si muove attraverso di esso, il tempo richiesto perché la luce passi da un punto all'altro della superficie della Terra, dipenderebbe dalla direzione in cui viaggia”. Poi proseguì, ricordando le asserzioni di Maxwell: “Fino ad ora non avevamo alcun metodo per misurare la velocità della luce che non comprendesse la necessità di far ritornare la luce sul suo cammino, per il quale motivo essa perderebbe circa tanto quanto ha guadagnato nell'andata. Poiché la differenza dipende dal quadrato del rapporto fra le due velocità, secondo Maxwell, è troppo piccola per essere misurata”.

L'idea geniale di Michelson fu di ricorrere all’utilizzo della lunghezza d’onda della luce come unità di misura, valutando i tempi attraverso la variazione di fase osservata al punto di arrivo. In altre parole, usò il fenomeno dell'interferenza, che permetteva di misurare sena problemi gli effetti del secondo ordine in v/c attraverso lo spostamento delle frange di interferenza, in funzione del cammino ottico.

Ritardare la luce

L’idea di base era quella di inviare due raggi luminosi in direzioni perpendicolari tra loro che coprissero un percorso uguale. Essi si sarebbero mossi con velocità c. Tuttavia, il raggio che si muoveva nella stessa direzione della Terra attorno al Sole avrebbe dovuto "nuotare" lungo il vento dell’etere, una volta in moto contrario e una volta a favore, mentre il raggio a 90° l’avrebbe attraversato sempre avendolo perpendicolare.

Spieghiamoci meglio. Se l’etere esisteva ed era fermo rispetto alla Terra, chi si muoveva con la Terra doveva subire un vento di etere di intensità uguale e opposta al moto della Terra. Ossia, il vento dell’etere si doveva muovere con velocità –v. All’andata, al pari del nuotatore della favola, la luce avrebbe trovato un ostacolo nel propagarsi, mentre al ritorno avrebbe avuto un aiuto. In ogni caso il tempo totale  sarebbe stato maggiore di quello del “nuotatore” perpendicolare. Un cammino ottico più lungo avrebbe provocato uno sfasamento nell’onda luminosa, perfettamente misurabile attraverso il fenomeno dell’interferenza. Un’idea geniale e rivoluzionaria!

Qualche calcolo facile facile

 La Fig. 1 mostra lo schema dell’esperimento.

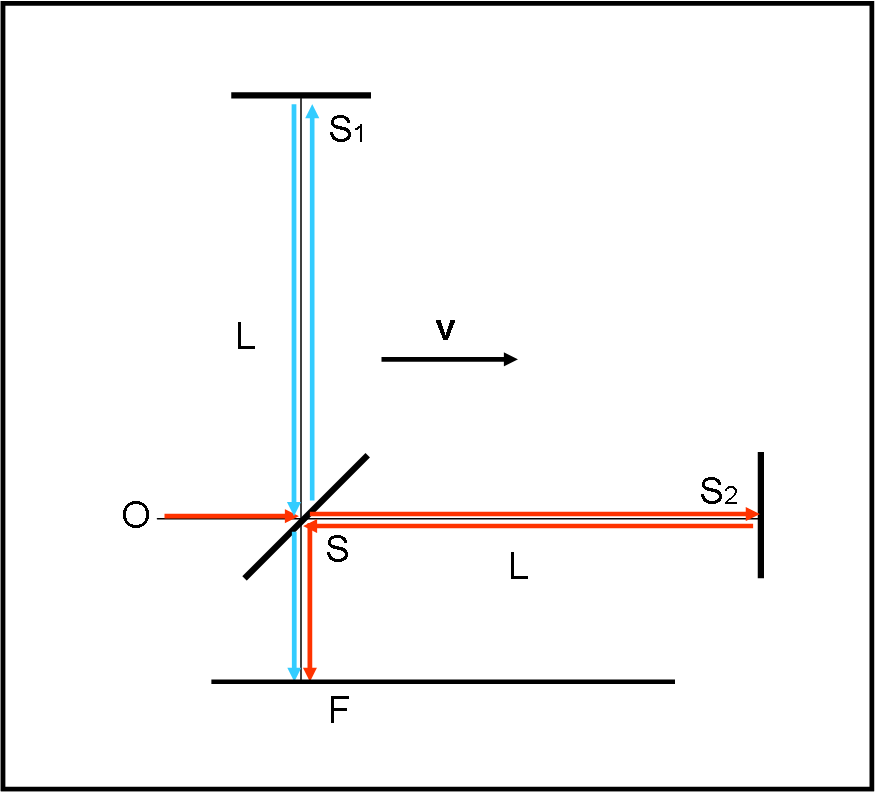
La luce parte da O e si dirige, nel verso del moto terrestre, fino a uno specchietto S inclinato di 45°, che permette al raggio di riflettersi e di attraversarlo (specchio semiriflettente). Il raggio, ancora perfettamente in fase, si sdoppia. Una parte di esso (quello blu, riflesso) si dirige verso S₁, specchio completamente riflettente, e torna indietro. Incontra nuovamente S, lo attraversa e va a formare l’immagine in F.

Il secondo raggio (rosso) prosegue verso S₂, un altro specchio riflettente, e torna indietro fino a S. Si riflette e si dirige verso F.

Aver colorato in rosso e blu i due raggi è solo di aiuto al disegno, in quanto la luce inviata non cambia la propria lunghezza d’onda lungo il percorso. Nel calcolo dei tempi impiegati dai raggi non si considerano quelli relativi al tratto OS e SF, dato che sono perfettamente identici tra loro. Ci limitiamo, quindi, solo alla parte SS₁S e SS₂S. Le distanze SS₁ e SS₂ sono uguali e valgono L (ma poco cambierebbe concettualmente anche se fossero diverse).

Cominciamo con il raggio rosso. Il tempo impiegato tra andata e ritorno da S a S₁, e viceversa, sembrerebbe veramente banale da scrivere:

t₁ = 2 L/c

Vedremo tra poco che questa relazione, usata subito da Michelson, non è esatta e fu corretta solo in seguito.

Passiamo, momentaneamente, al raggio blu che attraversa, all’andata, lo specchio S e percorre la  lunghezza L fino ad arrivare a S₂, dove viene riflesso. In questo caso, dobbiamo fare entrare in azione il vento dell’etere. All’andata la velocità è data da c – v, mentre al ritorno è data da c + v (come abbiamo già visto precedentemente):

t_2A= L(c – v)

t_2R= L(c + v)

t₂ = L/(c – v) + L/(c – v)

maneggiando un po’ la formula, come già fatto all’inizio, si ottiene:

t₂ = 2L/(c² – v²) = 2L/(c (1- v²/c²)) = 2Lγ²/c          …. (1)

ponendo (guarda caso…)

γ = 1/(1- v²/c²)^1/2

Ci fermassimo qui, potremmo dire facilmente che t₂ > t₁. Tuttavia, non possiamo dimenticare il fatto che t₁ è SBAGLIATO. La ragione sta nel fatto che lo specchio S si muove con la Terra (qualcosa di simile all’orologio di luce…) alla velocità v,  e il raggio che va da S a S₁ è costretto a muoversi “in diagonale” sia all’andata che al ritorno. Per calcolare esattamente il tempo t₁, bisogna, allora, fare intervenire il teorema di Pitagora e guardare la Fig. 2.

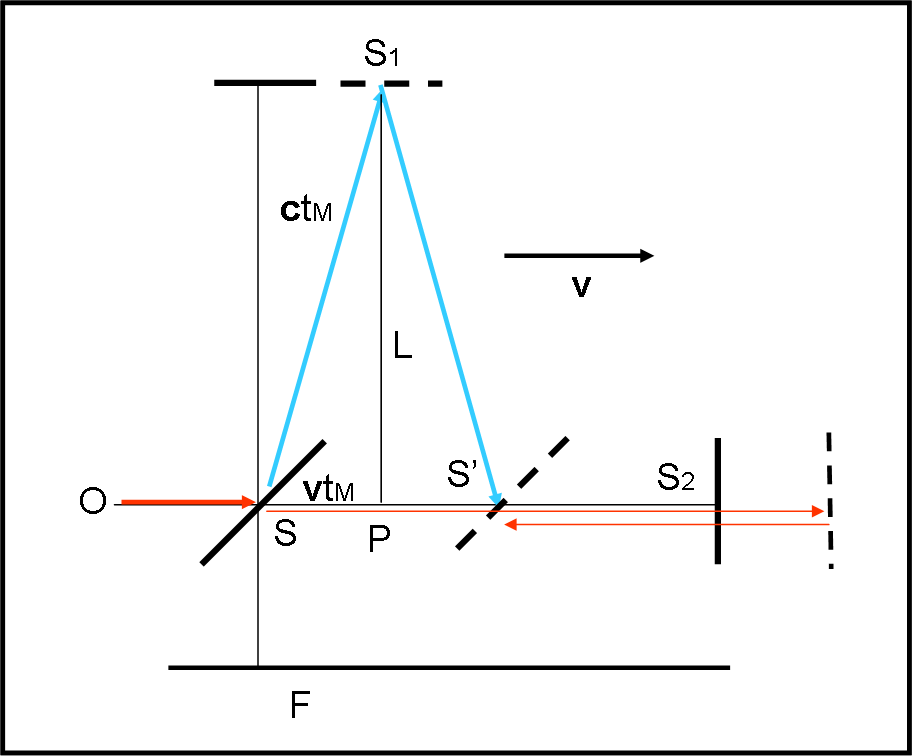
Si ha subito che il tempo totale t₁ è dato dalla somma del tempo impiegato per arrivare da S a S1 e di quello impiegato per andare da S1 a S’ (posizione finale dello specchio S). Ma i due tempi sono uguali (la stessa cosa che capitava per il nuotatore che attraversava il fiume) e quindi il tempo totale t₁ è il doppio del tempo impiegato per andare da S a S1. In poche parole, calcoliamo t_M, il tempo impiegato per andare da S a S₁, e poi lo raddoppiamo. Per fare ciò basta applicare il teorema di Pitagora al triangolo SS₁P.

SS₁² = SP² + L²

c²t_M² = v²t_M² + L²

t_M² = L²/(c² – v²)

t_M = L/(c² – v²)^1/2

t₁ = 2t_M = 2L/(c² – v²)^1/2

t₁ = 2L/c (1 – v²/c²)^1/2

t₁ = 2Lγ/c                                   …. (2)

E’ immediato notare che t₁ risulta sempre minore di t₂ e quindi i tempi impiegati dai due raggi sono decisamente differenti (anche se per quantità dell’ordine di v²/c^2.).

Facciamo la differenza tra i due tempi, ossia facciamo la differenza tra la (1) e la (2):

t₂ – t₁ = 2Lγ²/c - 2Lγ/c               …. (3)

La strumentazione poteva essere ruotata, in modo che il braccio diretto verso il moto della Terra si venisse a trovare a 90° rispetto a prima e i tempi si sarebbero invertiti. In tale modo si otteneva uno sfasamento doppio. Moltiplicando per c si aveva la differenza di cammino ottico nei due casi.

Δ₀ = 2Lγ² - 2Lγ

Δ₉₀ = 2Lγ - 2Lγ²

Dividendo la loro differenza per la lunghezza d’onda usata (giallo), si ricavava lo spostamento n delle frange di interferenza (assumendo, come già detto, un etere fermo rispetto alla Terra).

n = (Δ₀ - Δ₉₀)/λ

Nell’esperimento, la lunghezza L era di 11 metri (facendo andare avanti e indietro la luce per parecchie volte), mentre λ = 500 nm.

Ne risultava uno spostamento atteso delle frange di 0.44. Un qualcosa di estremamente ben visibile!

E, invece, niente!

Come spiegare il fallimento?

Si cercò di darne una spiegazione, ma risultò estremamente difficile. Si poteva dire che l’etere si muoveva con la Terra, ma in questo caso (come già detto QUI) si sarebbe andati contro l’aberrazione della luce. Si tentò anche con qualche via di mezzo, ma le spiegazioni risultavano prive di senso fisico. Una spiegazione più valida venne data da Fitzgerald (1889) e da Lorentz (1892), ipotizzando che le distanze si contraessero nel verso del moto. Questa contrazione la conosciamo molto bene ed è data dal fattore γ. In parole più tecniche, la lunghezza nel verso del moto terrestre sarebbe diventata:

L_c = L/γ

In verità, se andiamo a sostituire L_c al valore di L, per il tragitto nel verso del moto, la (3) diventa:

t₂ – t₁ = 2L_cγ²/c - 2Lγ/c = 2Lγ/c - 2Lγ/c = 0

Lo spostamento delle frange si annullerebbe proprio!

Questa ipotesi si basava sul fatto che i campi elettrostatici si deformavano quando erano in movimento. Tuttavia, a quei tempi, questa spiegazione apparve subito come una soluzione  “ad hoc”, non basata su conoscenze fisiche accettabili (poco si sapeva delle forze intermolecolari). Solo Einstein, nel 1905, riuscì a distruggere questa critica, dimostrando che non vi era alcuna necessità di muoversi attraverso l’etere per avere una contrazione delle lunghezze. Bastava cambiare completamente le idee di spazio, tempo e simultaneità e descrivere la relatività ristretta, assumendo una velocità della luce costante in ogni sistema di riferimento!

Einstein distrugge l’etere e, quindi, in particolare, l’essenza fisica della contrazione. Un fenomeno dovuto solamente al sistema di riferimento. Tuttavia, come già detto altrove, l’esclusione di un mezzo che permeava tutto l’Universo non lo soddisfaceva del tutto: all’etere, in pratica, sostituì il concetto di campo, le cui equazioni descrivono lo spaziotempo attraverso la relatività generale. In qualche modo, questo concetto riporta la contrazione verso un significato nuovamente fisico.

Chi vivrà vedrà e (forse) saprà...

 

Volete vedere Gatto Gualtiero (con le sue fusa) che si "propaga" su Alan, mentre ci racconta il fallimento più importante della storia della Fisica? Eccolo QUI!