Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo

 

Vediamo cosa avrebbe fatto Archimede per risolvere questo quiz… fermo restando che sono ammesse alcune varianti. L’importante è il concetto di fondo e la velocità di Pegaso & co. Leggetelo perché è di grande aiuto per la parte "seria" che seguirà...

Innanzitutto, pone uno specchio piano a una distanza di 10 km dalla sua posizione di misura. Di specchi ne aveva a iosa e per lui era uno scherzo farne uno anche piuttosto grande. Lo specchio era, ovviamente, sistemato perpendicolarmente alla linea immaginaria che lo univa ad Archimede. Per misurare la distanza, si dice che Archimede abbia veramente usato un dromedario, stretto parente di quello di Eratostene.

La misura sarebbe stata fatta quando il Sole era perfettamente alle spalle di Archimede, sulla stella linea Archimede-specchio. Sembra che una configurazione di questo tipo sia stata ottenuta aggiungendo un po’ di specchi (anche se non necessari, ma Archy era un vero fanatico…) e un diaframma che limitasse le dimensioni del Sole, riducendolo a un punto luminoso.

In poche parole, Archimede, specchio e Sole erano piazzati come in Figura 1.

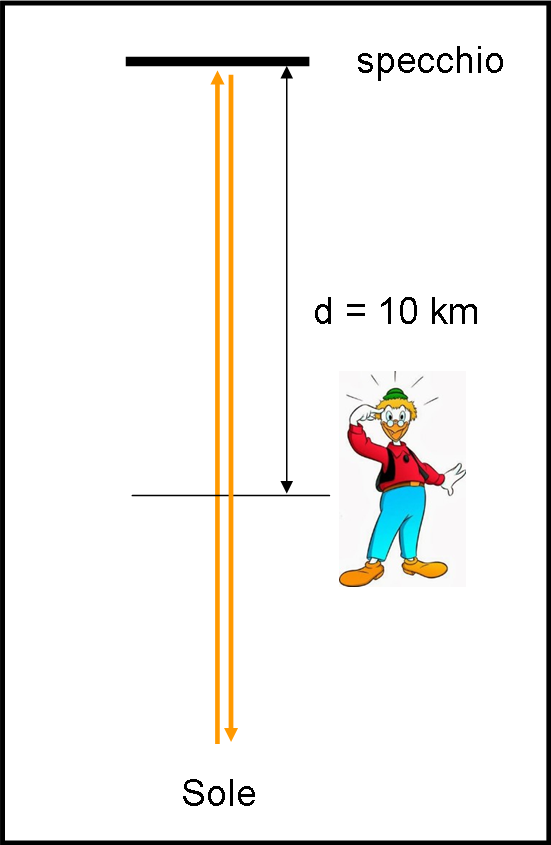
I raggi solari, molto limitati, sarebbero tornati perfettamente indietro fino a raggiungere nuovamente Archimede. Se chiamiamo c (celeritas) la velocità della luce, vale la relazione:

t_R – t_A = 2d/c

con t_A e t_R i  tempi di andata e di ritorno della luce da Archimede

Archimede aveva a disposizione solo clessidre e orologi ben poco precisi e, di conseguenza, sapeva benissimo di non poter misurare il tempo in cui la luce avrebbe percorso il tratto Archimede-specchio più quello di ritorno specchio-Archimede. Infatti, oggi sappiamo bene che la velocità della luce vale circa 300 000 km/s. Il che vuole dire che avrebbe percorso 2·10 = 20 km in un tempo pari a:

t_R – t_A = 20/300 000 = 0.0001 secondi (circa)

qualcosa di impensabile anche per una clessidra di precisione (ma anche per i nostri orologi da polso…).

Era, quindi, necessario fare sparire il tempo dalla misura. Per ottenere ciò doveva far svolgere nello stesso tempo una qualche altra azione, più facilmente misurabile.

Ed ecco, allora, chiamare in soccorso il cavallo Pegaso (gli deve essere costato una bella cifra!) con tre amici della stessa forza fisica. Si sapeva che la velocità dei quattro cavalli avrebbe raggiunto i 540 km/h, anche trasportando un peso non indifferente. Descriviamo, allora, qual è questo “peso” supplementare. Innanzitutto una biga e due soldati muniti di due scudi lavorati in modo perfetto: i loro bordi erano lisci e dritti come pochi, sicuramente spaccavano il millimetro e anche meno.

Il sistema cavalli-biga-soldati con lo scudo avrebbe dovuto passare a grande velocità davanti ad Archimede, in direzione perpendicolare alla congiungente Sole-specchio, come mostrato schematicamente in Fig. 2. Nella figura non si sono disegnati i due soldati che si sono nascosti abilmente dietro ai propri scudi.

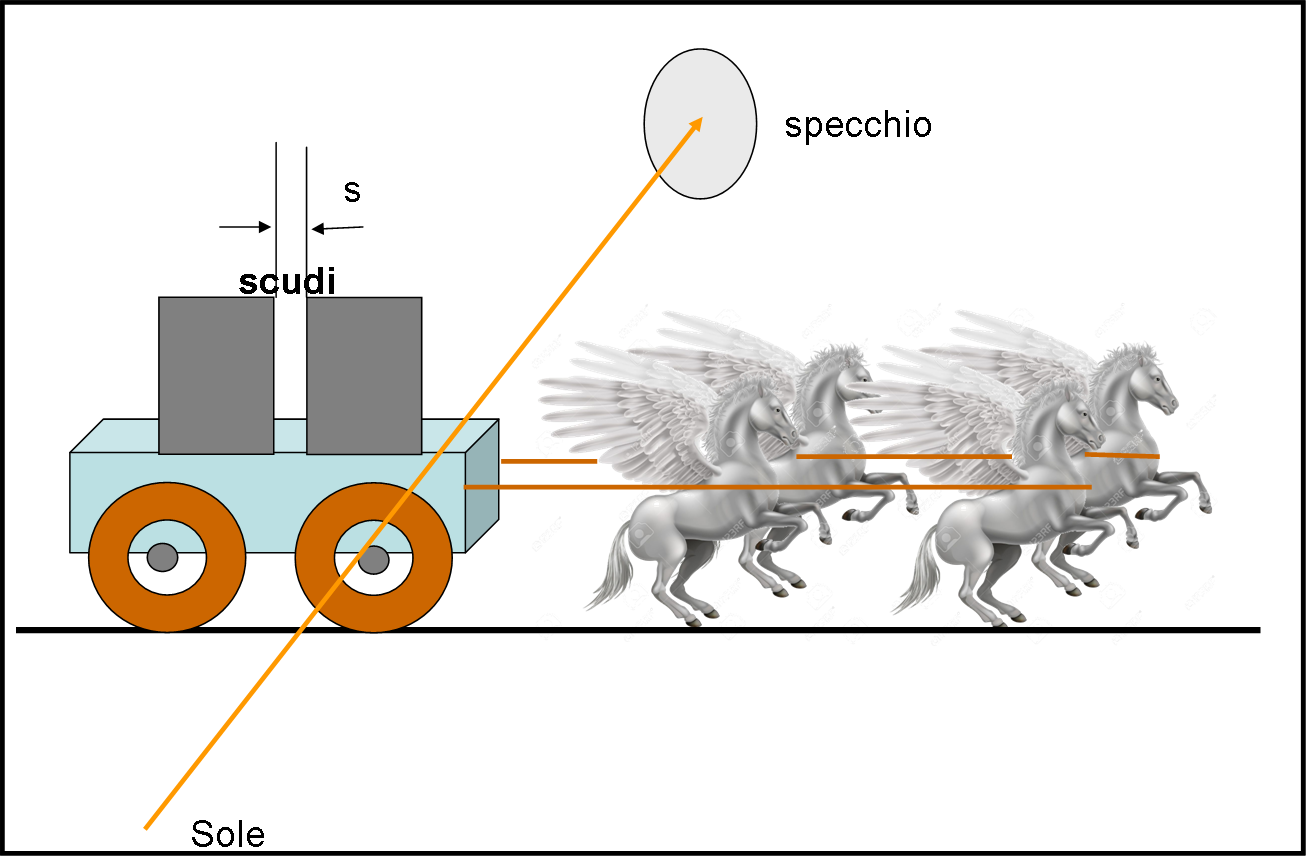
Adesso, le cose si complicano un pochino, ma Archimede era o non era un genio? Lui ragiona e pensa: “Se la luce solare incontra uno scudo non riesce a raggiungere lo specchio e io, guardando in quella direzione, non vedrò nulla. Se, invece, la luce passa tra uno scudo e l’altro, vedrò il riflesso del Sole causato dallo specchio. Devo fare in modo di mettere i due scudi a una distanza, l’uno dall’altro, tale che, mentre i cavalli sono al galoppo, sia sicuro di vedere a un certo istante la prima luce dopo il buio causato dal primo scudo." Spieghiamoci meglio…

Cominciamo col mettere gli scudi troppo vicini tra loro (s molto piccolo). Quello che succede è raffigurato in Fig. 3.

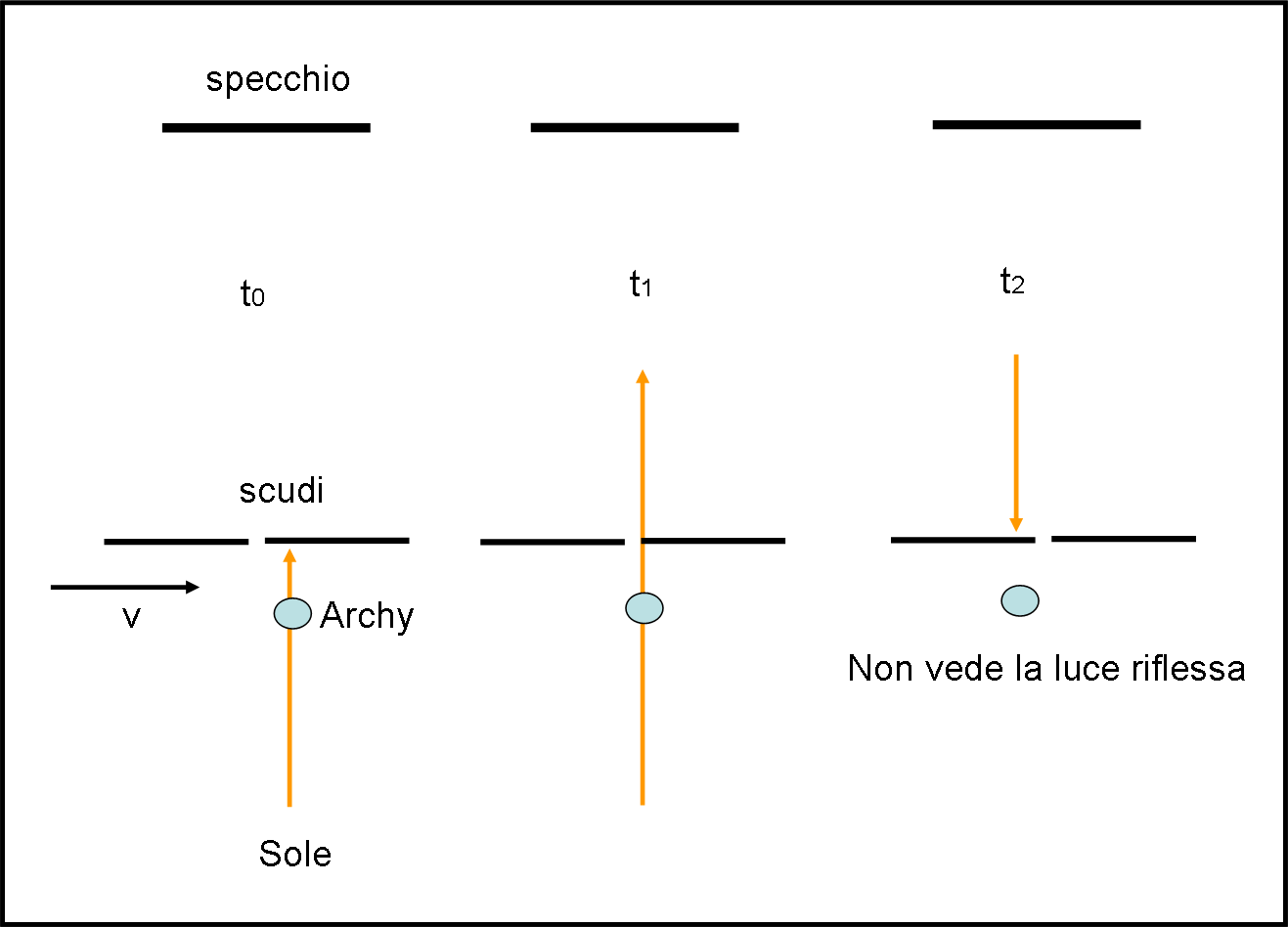
Al tempo t₀ il primo scudo blocca la luce del Sole e Archy non vede niente. Al tempo t₁ la luce riesce finalmente a passare nello spazio tra i due scudi. Quello è il raggio che Archy deve vedere tornare dopo essersi riflesso sullo specchio. Ma, la luce, per veloce che vada, impiega un certo tempo per tornare indietro. Lo spazio s è troppo piccolo e quando questo raggio ritorna, al tempo  t_2, all’altezza degli scudi non trova più lo spazio libero, ma il secondo scudo. Niente da fare, Archy non riesce a vedere la luce che torna indietro: per lui è sempre buio.

Facciamo, adesso, l’errore contrario, ossia lasciamo uno spazio troppo grande tra uno scudo e l’altro. Vediamo il risultato in Fig. 4.

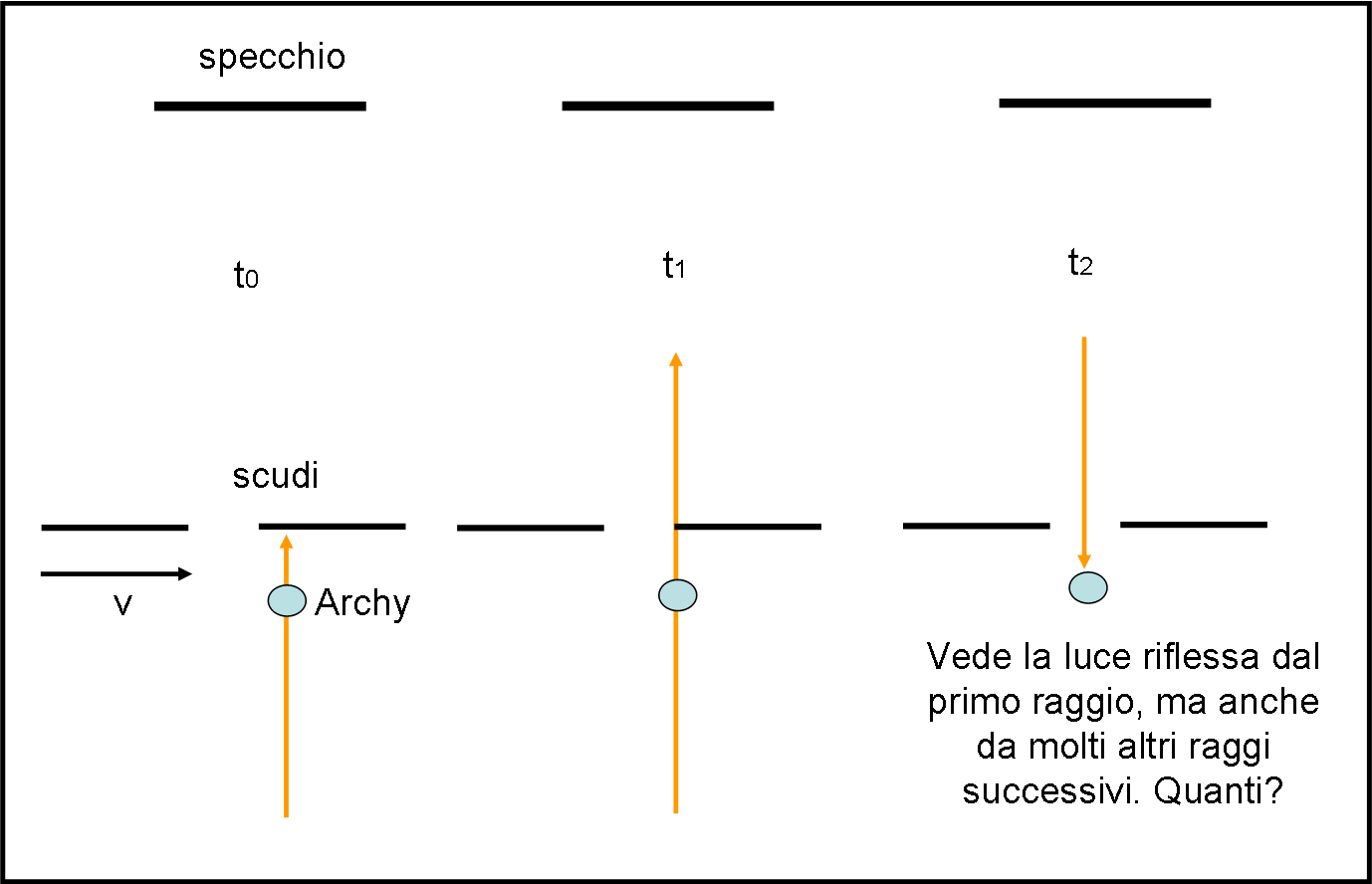
Al tempo t₀ il primo scudo blocca la luce, come nel caso precedente. All’istante t₁ il primo raggio riesce a passare. Quando torna indietro raggiunge lo spazio tra gli scudi al tempo t₂. Magnifico! No, non molto… anche negli istanti successivi Archy vede la luce riflessa e quindi è come se vedesse il secondo, il terzo, il quarto raggio e via dicendo. Non può certo sapere quante volte è successo e quindi non può concludere niente.

Pegaso e i suoi amici sono molto servizievoli (se ben pagati) e sono disposti a ripetere l’operazione un gran numero di volte. Ogni tentativo vede lo spazio diminuire sempre di più, in modo da passare dal secondo caso al primo. Stando molto attento, Archy nota un caso estremamente particolare: vede la luce solo per un istante brevissimo. Se lo spazio è solo leggermente più piccolo non vede più niente, se è solo un po’ più grande (e continua a crescere) nota che la luce riflessa rimane visibile sempre più a lungo. Lo spazio giusto da imporre ai due scudi è proprio quella che ha causato il lampo di luce più breve, subito dopo aver visto sempre buio. Le condizioni ideali sono quelle di Fig. 5.

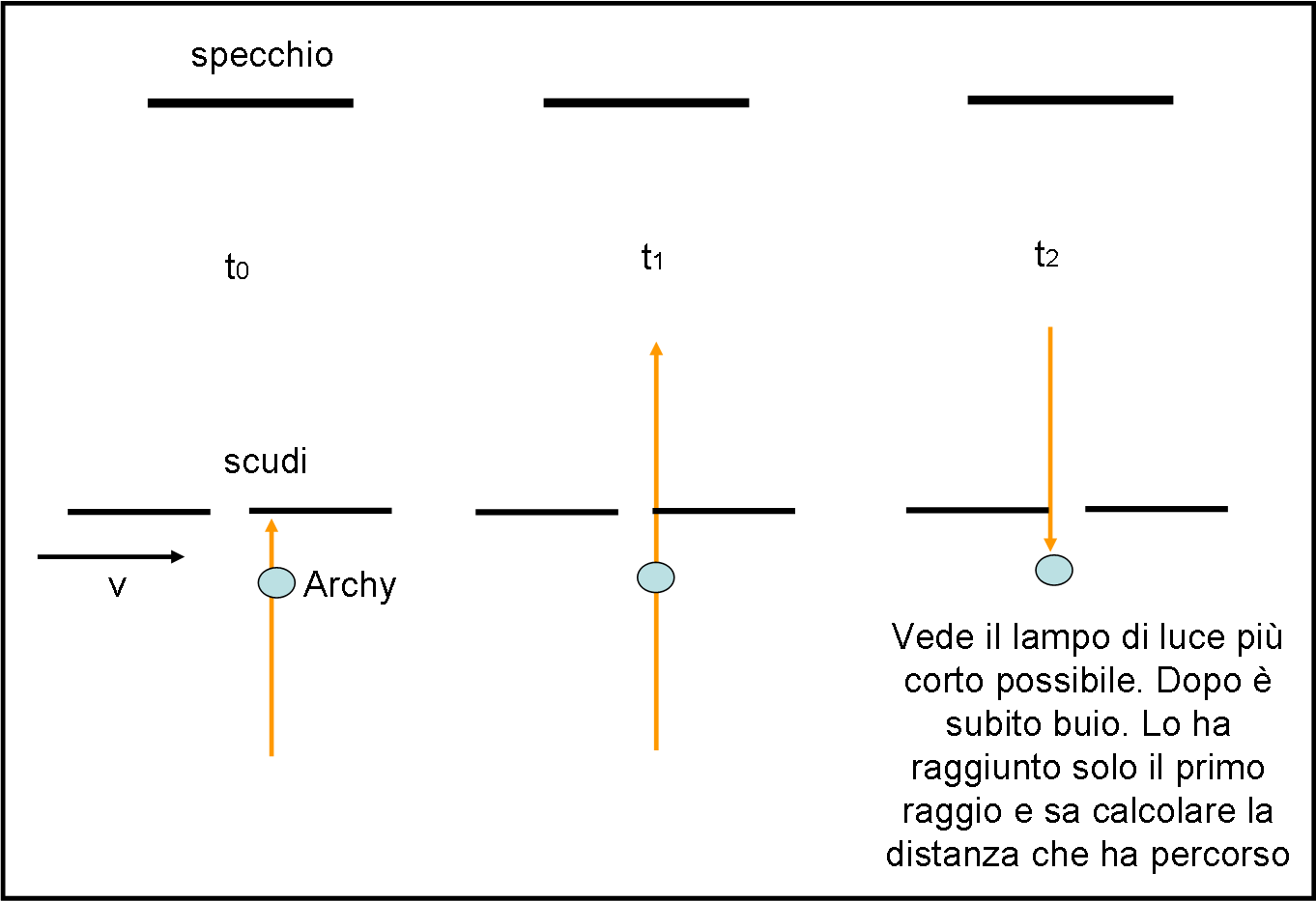
In t₀ succede sempre lo stesso. In t₁ il primo raggio passa dallo spazio vuoto. In t₂ il raggio riesce a passare “al pelo”, dato che quello successivo viene già bloccato dal secondo scudo. Eureka! Adesso sì che ci siamo. Abbiamo tutti i dati necessari a risolvere il problema.

Nello stesso intervallo di tempo che un raggio di luce impiega a passare nello spazio tra i due scudi e a tornare indietro fino ad Archy, Pegaso e i suoi amici si muovono di una lunghezza che è pari allo spazio tra i due scudi! Basta allora scrivere questo tempo in due modi, uno in relazione al percorso scudo-specchio-scudo, compiuto dalla luce, e l’altro in relazione allo spostamento degli scudi in funzione della velocità di Pegaso.

La prima relazione l’abbiamo già scritta:

t_R – t_A =  t₂ – t₁ = 2d/c                …. (1)

d è noto, mentre c è la grandezza da determinare.

La seconda è altrettanto semplice:

t₂ – t₁ = s/v                                 …. (2)

Ma v è la velocità costante di Pegaso, che è stata misurata su spazi e tempi ben più lunghi e vale 540 km/h, s non è altro che la distanza tra gli scudi che dà luogo al lampo più breve. Archy lo ha misurato e ha trovato s = 1 cm = 0.01 m = 0.00001 km. Trasformiamo la velocità di Pegaso in km/s. Si ha:

v = 540/3600 = 0.15 km/s

Basta allora uguagliare la (1) e la (2) (eliminando il tempo) e ricavare c:

2d/c = s/v

c = 2d v/s

c = 20·0.15/0.00001 = 300 000 km/s

Niente male! E bravo Archy, ma bravi anche Pegaso & co, senza dimenticare i due soldati e colui che ha lavorato gli scudi.

E bravi anche i maghi e maghetti vari…

Da qui a Fizeau il passo è breve…

 

In attesa che siano riuniti in un unico approfondimento, QUI trovate tutti gli articoli dedicati alla misura della velocità della luce finora pubblicati