Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

Risolviamo velocemente il quiz della pallina e del treno che, immagino, tutti siano stati in grado di risolvere anche senza scriverlo nei commenti (un grazie particolare a Edoardo e anche a Gianni). In realtà lo scopo era di riattivare certi concetti di base per affrontare il problema non banalissimo della forza di Coriolis. Consideriamo, quindi, questo breve articolo come la puntata ZERO di un discorso molto più ampio che tocca torri, aerei, cicloni e giostre varie.

La soluzione della prima parte è ovvia e si basa sul primo principio della dinamica: un corpo mantiene la propria velocità se non interviene alcuna forza a perturbarlo. Esso, da solo, ci dice che la pallina lasciata libera  deve mantenere la sua velocità, ossia quella del treno e del bambino (se è fermo sul treno). Già questo basta per affermare che, rispetto a un punto fisso esterno al treno (nella direzione opposta al suo moto), la pallina deve allontanarsi.

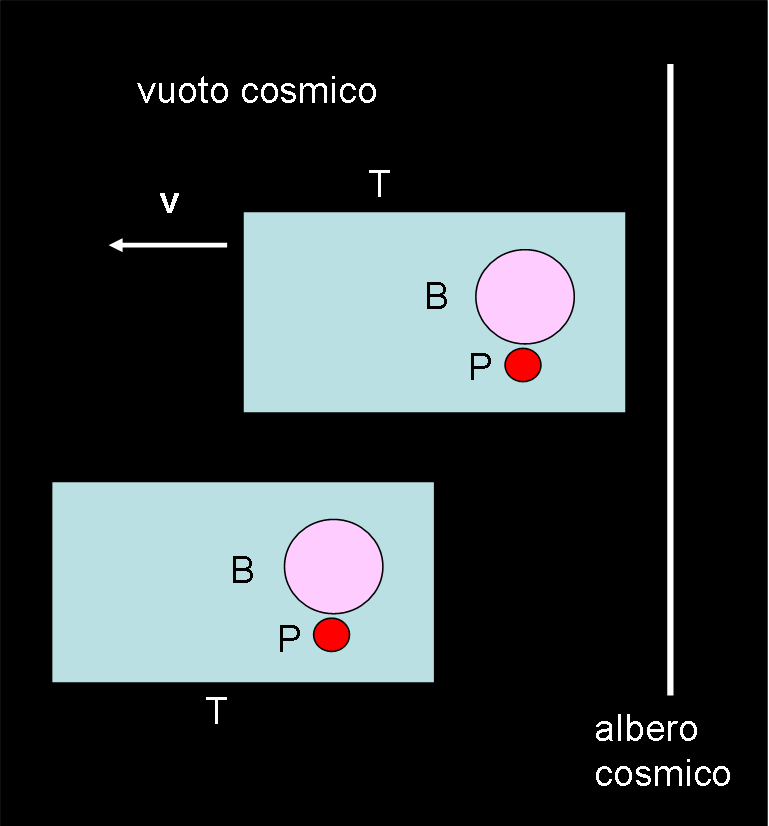
Questo primo risultato si applicherebbe benissimo a un treno T (molto schematizzato) che viaggi nello spazio a velocità v, lontano da qualsiasi oggetto celeste. La pallina P non subirebbe nessuna forza e rimarrebbe nella stessa posizione rispetto al bambino B (Fig. 1). In parole semplici, galleggerebbe senza cadere, sospesa nel vuoto. Tuttavia, rispetto a un punto fisso dello spazio (albero cosmico)la pallina si allontana.

Nel nostro caso, però, esiste una forza che agisce sia sul treno che sul bambino che sulla pallina: la forza di gravità. Il treno, però, non cade perché il suolo e le rotaie glielo vietano. Il bambino fa lo stesso, dato che i suoi piedi sono poggiati sul pavimento del treno. La pallina, invece, è libera di cadere obbedendo alla forza di gravità. Nel far questo, cerca anch’essa di raggiungere il terreno, per poi fermarsi a causa dell’attrito della terra che annulla la sua velocità (il treno va su rotaie lisce e queste non lo frenano).

Il moto della pallina, rispetto all’albero fermo, è quindi determinato da semplici formule cinematiche che tengano in conto sia la sua velocità orizzontale (quella del treno) sia la velocità leggermente crescente durante la caduta, dovuta alla gravità (una forza determina un’accelerazione che fa variare la velocità). Il moto finale è rappresentato da una mezza parabola con la concavità rivolta verso il basso (Fig. 2). Nella figura abbiamo visualizzato quattro istanti successivi, che poi sono stati inseriti tutti nel primo,  in modo da evidenziare il percorso effettuato dalla pallina. rispetto all'albero fisso. In realtà, l’accelerazione di gravità non è costante e dipende dalla distanza del corpo dalla Terra, ma noi possiamo tranquillamente considerarla costante (la famosa g).

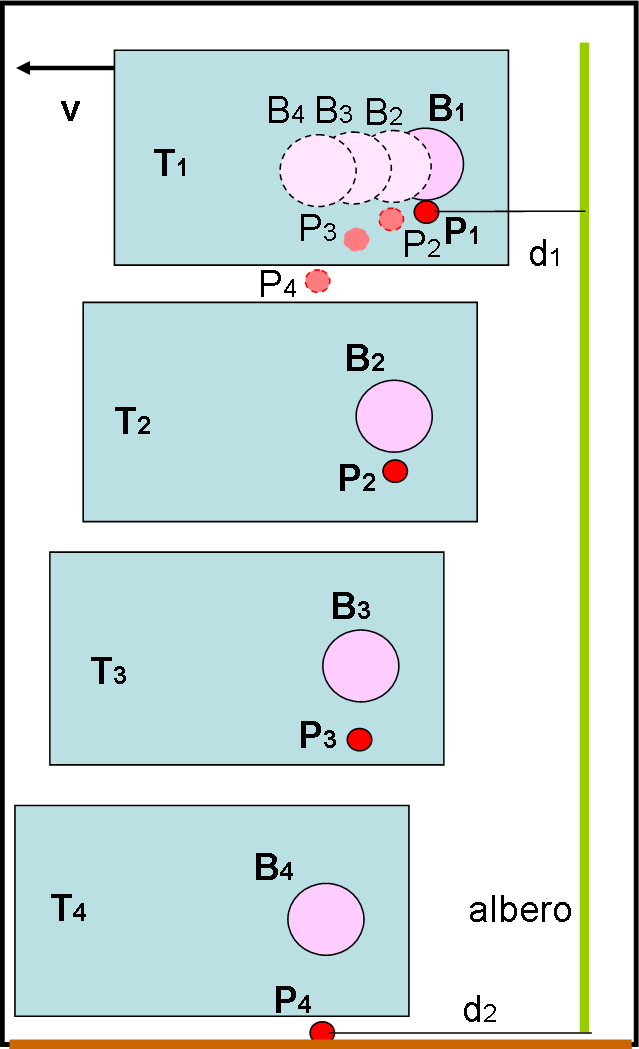
Ne segue che la pallina cade sicuramente più lontana dall’albero rispetto a quando è stata lasciata libera dal bambino. Più il treno va veloce e più la distanza cresce (l’accelerazione di gravità rimane sempre la stessa).

Tuttavia, merita fare una riflessione in più. Il bambino, se non guardasse l’albero, ma solo la pallina, la vedrebbe cadere in modo perfettamente verticale. Dato che anche lui si è spostato della stessa distanza rispetto all’albero. Ossia, sia che sia realmente fermo sia che sia in moto con velocità costante, il bambino vedrebbe sempre lo stesso fenomeno. Questo è sempre vero perché il treno si muove rispetto al suolo con una velocità costante e quindi rappresenta un sistema inerziale. Questo fatto è ben conosciuto ed è parte essenziale della relatività galileiana (anche se era già stata formulata da Giordano Bruno). In parole semplici, si può dire che i fenomeni della meccanica rimangono perfettamente uguali passando da un sistema inerziale a un altro. Ciò vuole anche dire che nessun esperimento di meccanica può far capire se ci si muove di moto rettilineo uniforme oppure no.

Anche se questo quiz è veramente di fisica elementare, ci permette di ribadire un concetto che ci tornerà estremamente utile in seguito: la velocità di un corpo cerca di mantenersi costante (principio di inerzia).

La seconda parte del quiz, sembrerebbe banalissimo. Se il treno è fermo appartiene allo stesso sistema di riferimento dell’albero e, di conseguenza, la pallina cadrebbe perfettamente verticale rispetto all’albero, mantenendo la sua distanza. In altre parole, agirebbe soltanto la forza di gravità.

Il problema è che, avvicinandosi al terreno, la velocità tangenziale della Terra dovuta alla sua rotazione diminuisce e la pallina, che è libera di mantenere la sua velocità tangenziale, cade più avanti rispetto al suolo, che si è spostato di meno. In poche parole, la pallina vede il suolo che scorre in senso opposto alla rotazione della Terra e dell’albero che è ancorato a lei. La pallina si avvicina all’albero, anche se di una quantità estremamente piccola, solo a portata di formiche o anche meno.

Per cominciare a prendere dimestichezza con questo fenomeno andate a leggere questa storia tragicomica ma molto istruttiva di Mauritius. Vi posso già preannunciare che tutto ciò capita perché la Terra non è, in realtà, un sistema inerziale e se si vuole spiegare un fenomeno come è visto da lei bisogna introdurre delle forze “fittizie” (ma che si sentono e come!). Una la conosciamo già molto bene ed è la forza centrifuga; l’altra l’andremo a spiegare, con molta attenzione e semplicità, ed è la forza di Coriolis. A lei si deve lo spostamento verso est della pallina, la correzione di rotta degli aerei, la formazione dei cicloni e degli anticicloni, lo sbandamento che si subisce nei tram o nei treni quando curvano, e molte altre cose, ma non la rotazione dell’acqua nello scarico del lavandino!

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis