Questo lungo articolo è stato inserito nell'approfondimento dedicato alla velocità della luce che tratta l'argomento in modo organico

 

Parliamo della determinazione della velocità della luce e di come abbia influenzato pesantemente la scomparsa dell'etere. Questo articolo unisce l'esperienza "fallimentare", ma fondamentale, di Michelson e Morley con i vari tentativi astronomici e terrestri utilizzati per la determinazione della velocità della luce. Al suo interno, anche due quiz risolti allegramente.

Un quiz per i figli

Un grande scienziato propose questo QUIZ ai suoi figli:

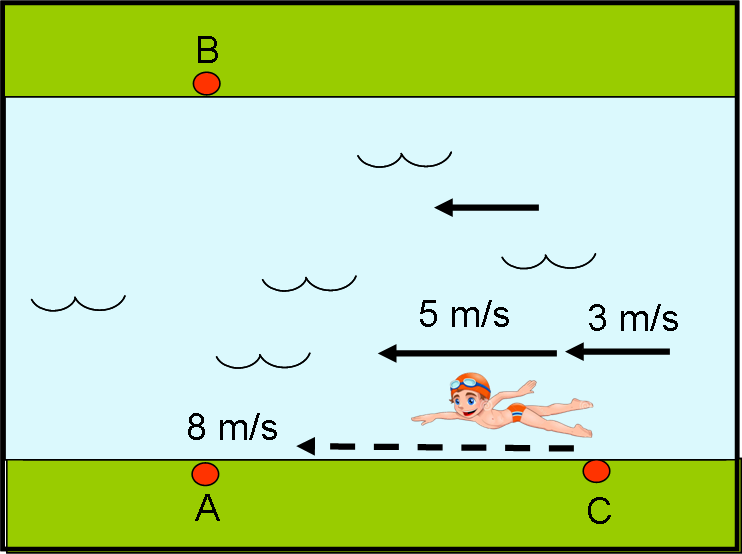
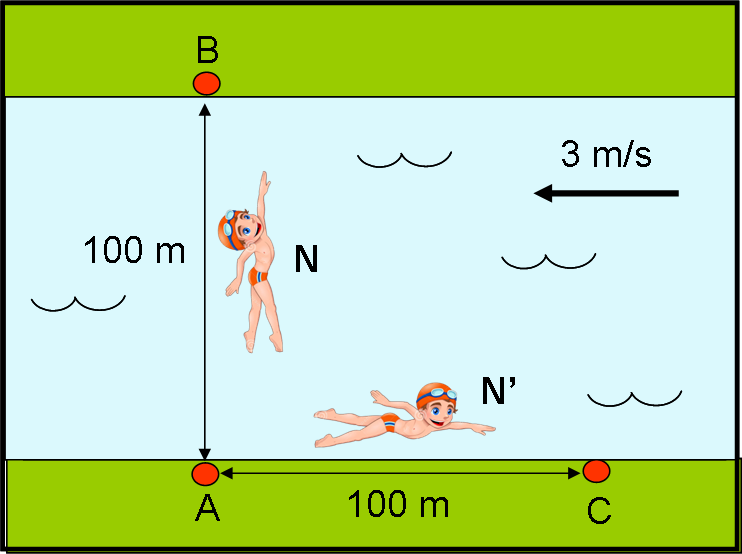
Supponete di essere presso un fiume che è largo 100 m. Siete due ragazzi (N e N') che nuotate alla stessa velocità di 5 m/s. Il fiume ha una corrente da destra verso sinistra pari a 3 m/s. Il primo di voi parte da A e deve attraversare il fiume toccando il punto B e tornare al punto A. Il secondo deve nuotare lungo la sponda del fiume da A fino a C e tornare in A. La distanza tra A e C è uguale a quella tra A e B. Chi di voi impiegherà meno tempo? 

Un semplice calcolo e la soluzione è a portata di ... bracciata!

Questo quiz, apparentemente di estrema semplicità, è valso un Premio Nobel allo scienziato. Il suo nome: Albert A. Michelson. Il metodo usato: fantastico. Il risultato: negativo, ma ha cambiato la fisica.

Continuiamo a usare l'esempio per bambini (o poco più) e solo dopo torneremo all'esperimento vero e proprio, con la dovuta serietà e attenzione

Impostiamolo, quindi, proprio come una favola. Ciò comporta qualche inesattezza,  di secondaria importanza rispetto al concetto di fondo. Le favole, spesso, possono dire molto di più che la la fredda e precisa realtà. Comunque, dopo la favola seguirà una descrizione di carattere scientifico. Per adesso, seguendo il nostro stile, via libera a una favola vietata ai maggiori di X anni, con X che tende a infinito…

Uno scienziato e due fotoni

In un mondo incantato (il nostro Universo), esistono due strani folletti, che ormai conosciamo molto bene, avendoli spesso chiamati per nome: fotoni. Essi sono molto allegri e spesso dispettosi, ma hanno un compito veramente straordinario, quello di trasportare la luce. Senza di loro non potremmo vedere né i nostri familiari, né gli animali, le piante, il nostro pianeta, il Sole, le stelle e le galassie. Insomma, saremmo completamente ciechi. I fotoni sanno quanto sono importanti, per cui cercano di correre al massimo delle loro possibilità. Ci riescono benissimo, in quanto, nell’Universo, non c’è niente che vada più veloce di loro. Essi percorrono, infatti, ben 300 000 chilometri in un secondo, ossia raggiungono quella che noi chiamiamo velocità della luce.

Un lavoro veramente stressante. Pensate che per riuscire a raggiungere questa velocità in modo costante essi non si devono fermare mai. Anzi, possono esistere solo se corrono sempre al massimo. Non potremo mai dirgli grazie abbastanza e gli si possono facilmente perdonare alcuni scherzi e giochi che compiono con i loro amici elettroni.

Bene… conosciuti i nostri due eroi, vediamo per cosa un certo grande scienziato, di nome Michelson, pensò di utilizzarli. Potremmo considerarlo un vero mago con i suoi due assistenti…

Innanzitutto, un po’ di storia molto semplice. Il comportamento dei fotoni è alquanto bizzarro, come si diceva prima. Essi, a volte, sembrano delle vere e proprie particelle, ma, altre volte, si comportano come onde (questa favola ce l'hanno raccontata Fotino e i suoi fratelli) e gli scienziati hanno cambiato idea molte volte a riguardo. In realtà le due cose sono del tutto compatibili, ma ai tempi del nostro scienziato non si era ancora compresa appieno questa capacità dei piccoli fotoni (e di molti altri loro piccoli amici). A quei tempi si parlava di onde, come quelle del suono, capaci di trasmettere i rumori. Onde, capaci di trasmettere la luce.

Tuttavia, sorgeva un grave problema: le onde del suono si propagano perché c’è l’aria. In parole ancora più semplici: loro mettono in vibrazione l’aria che ondeggia, appunto, e permette di trasportare il segnale rumoroso. Qualcosa di molto simile alle onde del mare che si propagano nell’acqua e la fanno alzare ed abbassare al loro passaggio.

Il che voleva dire che se la luce, intesa come onda, poteva viaggiare tra le stelle e arrivare fino ai nostri occhi, doveva esistere una specie di acqua o aria che potesse vibrare. Un qualcosa che doveva impregnare tutto l’Universo. Gli scienziati l’avevano chiamata etere, una specie di sostanza molto rarefatta che non desse fastidio al movimento dei corpi celesti, ma che permettesse, comunque, di poter vibrare e trasportare le onde luminose.

Il signor Michelson decise di provare l’esistenza dell’etere attraverso l’utilizzo dei suoi due fotoni sempre disponibili a giocare. Per non complicare troppo le cose, immaginiamo che i fotoni siano proprio particelle che continuino a saltellare su è giù rispetto a una linea diritta, in modo da simulare un’onda dell’etere che si alza e si abbassa, come vediamo nella Fig. 1.

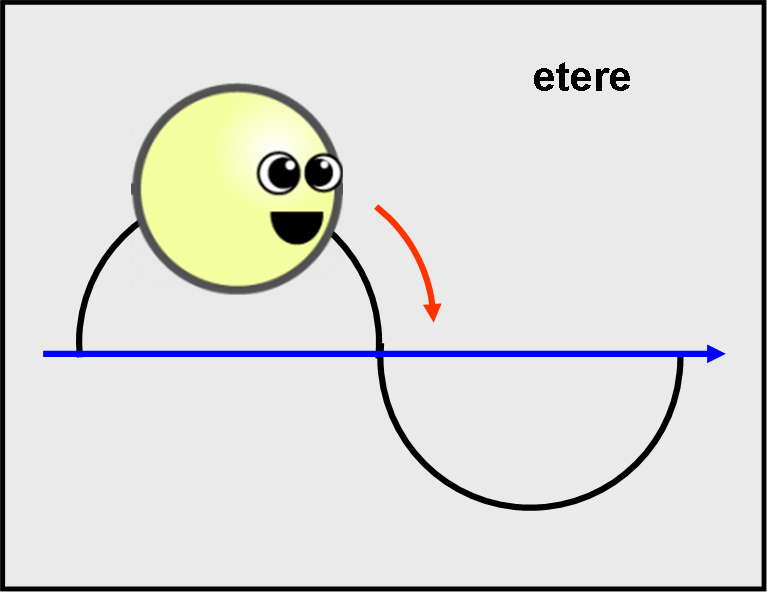
Lo stesso signor Michelson pensò che la Terra, durante il suo moto attorno al Sole, doveva muoversi attraverso l’etere, immaginato sempre immobile, e, quindi, doveva succedere la stessa cosa che a noi capita quando corriamo velocemente. Anche se non c’è vento, sentiamo l’aria che ci sbatte in faccia. In questo modo ci accorgiamo che attorno a noi c’è aria, qualcosa di materiale, anche se è talmente rarefatta da non accorgercene normalmente, quando siamo fermi. La stessa cosa doveva succedere alla nostra Terra mentre si muoveva attorno al Sole. Lei viaggiava nell’etere e quindi muovendosi a una certa velocità doveva venire investita dall’etere che le sbatteva contro, come viene rappresentato in Fig. 2.

In altre parole, se la Terra si muovesse con una certa velocità, è come se si considerasse ferma e venisse investita da un vento di etere con pari velocità, ma diretto in senso contrario al moto della Terra. La stessa cosa che capiterebbe se, correndo, pensassimo di essere fermi e sentissimo il vento dell’aria colpirci con la stessa velocità con la quale in realtà stiamo correndo.

Ovviamente, se esisteva l’etere, anche i due fotoni scelti da Michelson dovevano subire l’effetto dell’etere. Se viaggiavano nella direzione del moto della Terra sarebbero stati investiti dal vento dell’etere e avrebbero dovuto trovare un po’ di resistenza nel correre, se invece fossero andati in senso contrario sarebbero stati aiutati nella loro corsa.

Per spiegare ancora meglio l’esperimento di Michelson, immaginiamo di essere nei pressi di un fiume. Esso ha una certa corrente, ossia la sua acqua è trascinata verso una direzione (dalla sorgente alla foce). La corrente del fiume simula molto bene ciò che fa il vento dell’etere: un qualcosa che si oppone al movimento se si va controcorrente e che l’aiuta se va in favore di corrente.

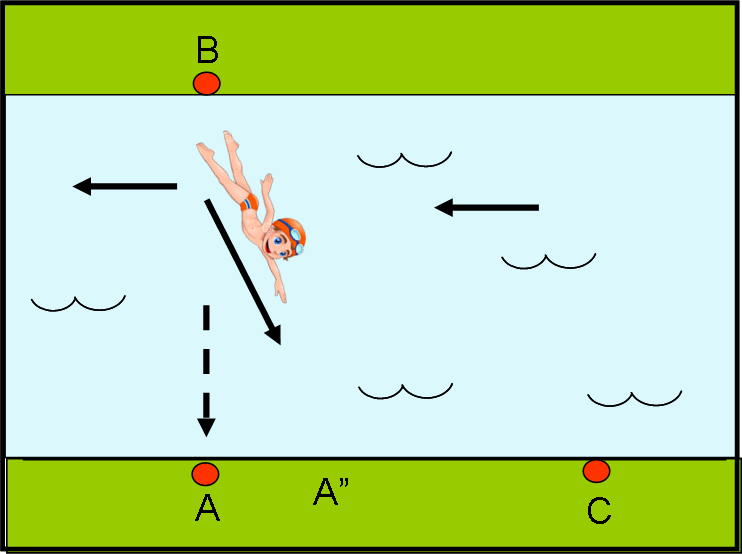
Prendiamo due nuotatori, ossia i nostri due fotoni. Con un colpo di bacchetta magica blocchiamo la corrente del fiume in modo che esso diventi una piscina con l’acqua immobile. Dopodiché, impostiamo una bella gara tra i due fotoni N e N’ (travestiti da veri nuotatori), come mostra la Fig. 3. Il primo deve partire da A, attraversare il fiume, toccare B e tornare esattamente indietro in A. Il secondo deve, invece, percorrere la distanza da A e C, vicino alla riva del fiume, e tornare in A. La distanza tra A e C (d) è ESATTAMENTE uguale a quella tra A e B. Vince la gara chi arriva per primo.

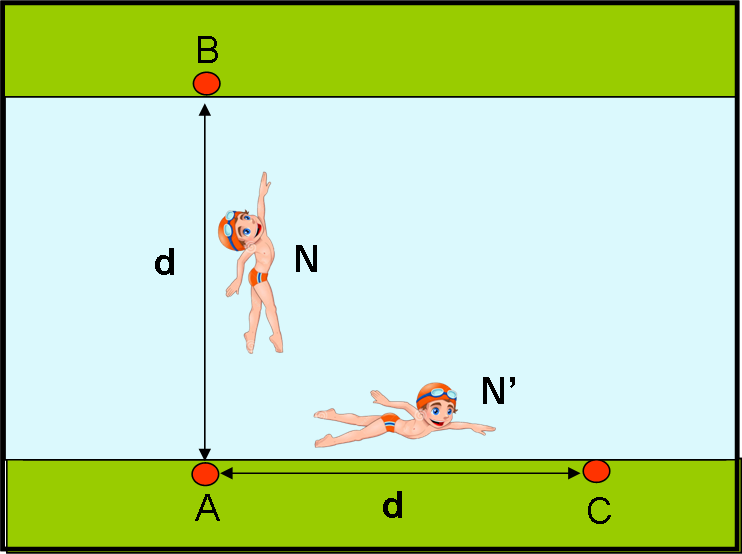
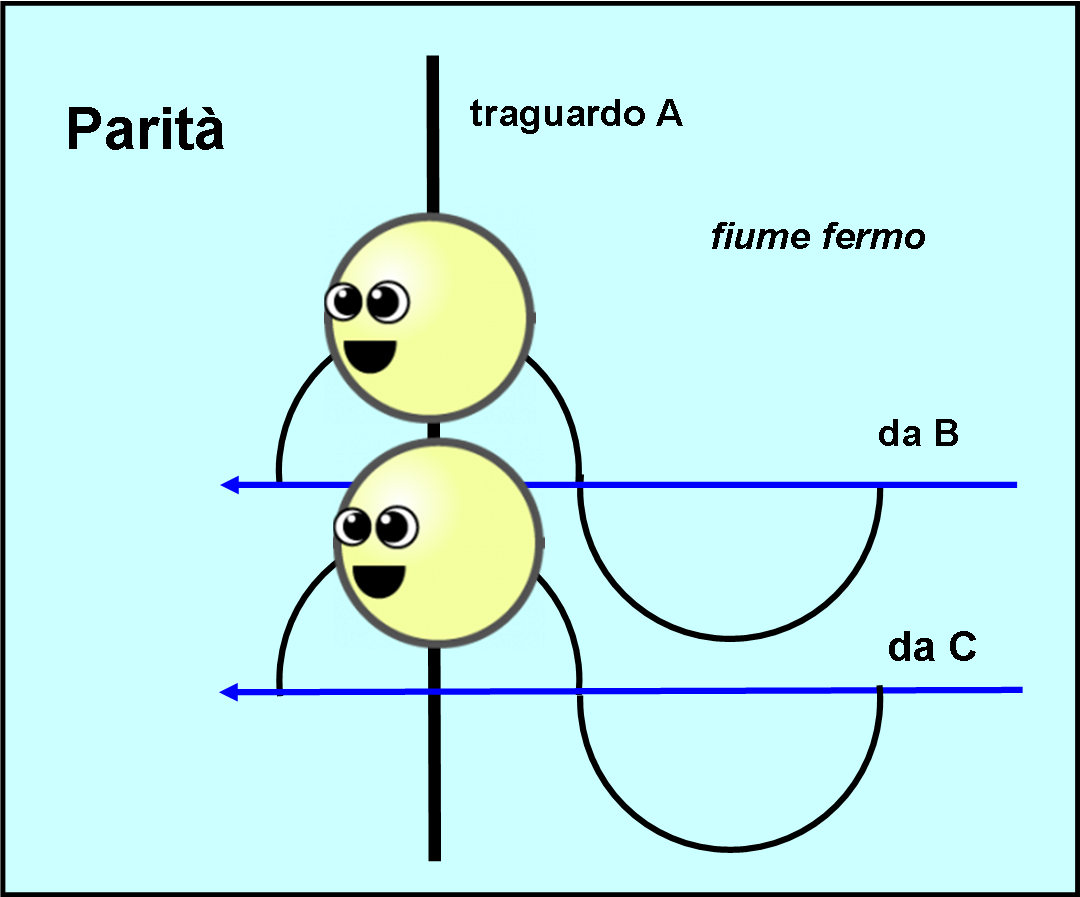
I fotoni sono contentissimi di questo gioco e non vedono l’ora di eseguirlo. Partono nello stesso istante da A e, saltellando, saltellando (nuotando, nuotando), tornano al punto di partenza. Michelson si accorge della parità dato che i fotoni effettuano lo stesso identico saltello quando arrivano al traguardo. L’acqua è ferma, le distanze uguali e la velocità dei fotoni esattamente la stessa (tutti i fotoni viaggiano alla stessa velocità): non poteva ottenere niente di diverso (Fig. 4).

Fin qui tutto bene. Adesso, la faccenda si complica, dato che al fiume viene permesso di scorrere tranquillamente. In altre parole, inseriamo il vento dell’etere, ossia la corrente del fiume. Vediamo passo dopo passo cosa capita ai nostri due fotoni. Consideriamo per primo quello che attraversa il fiume (Fig. 5a).

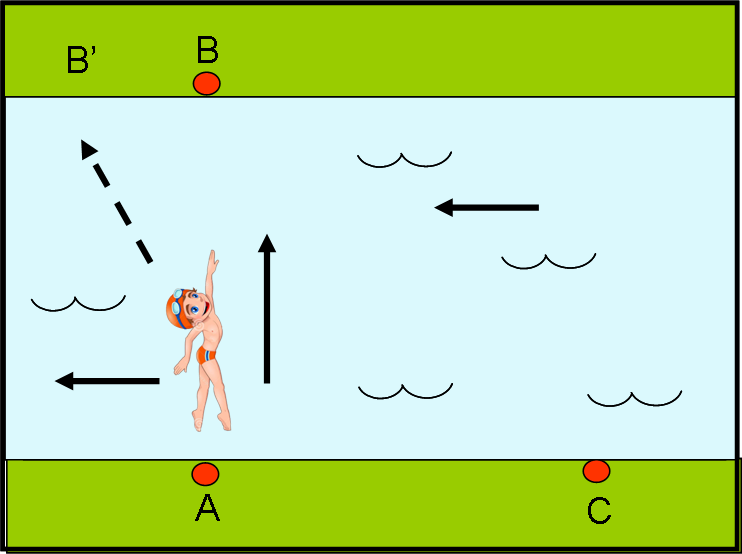
Il fotone non è uno sprovveduto e sa benissimo che se si dirigesse nella direzione in cui vede B alla partenza sarebbe ben presto trascinato dalla corrente verso sinistra e toccherebbe l’altra sponda in un punto diverso (B’). I fotoni sono piccolissimi, ma molto intelligenti e non è da meno il nostro nuotatore. Lui sa che deve dirigersi contro corrente di un certo angolo (verso B”), in modo che la sua velocità in quella direzione si sommi a quella della corrente del fiume e lo porti esattamente in B (Fig. 5b).

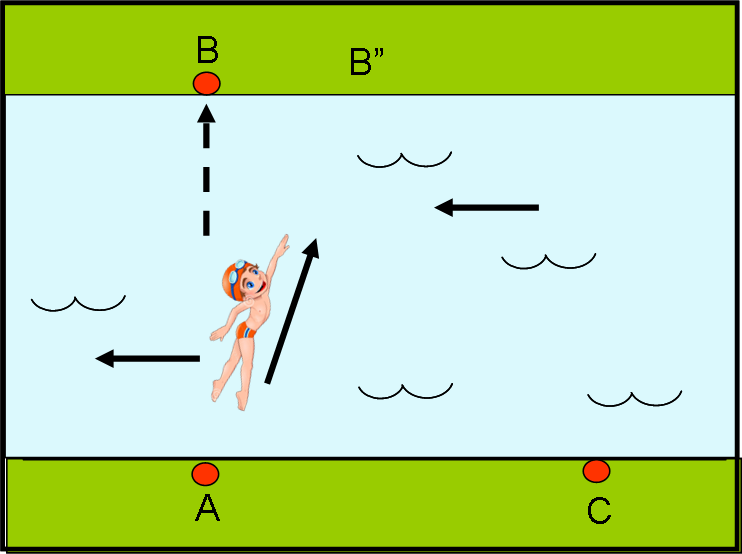
Mentre va verso destra viene costantemente spostato verso sinistra dalla corrente fino a raggiungere esattamente B. La stessa cosa deve fare al ritorno in modo perfettamente simmetrico (Fig. 5c).

Per coloro che conoscono il teorema di Pitagora è facile capire a che velocità va effettivamente il fotone. Se, ad esempio, la sua velocità fosse 5 m/s e quella del fiume 3 m/s, si otterrebbe una velocità di 4 m/s (√(5² – 3²) = √ (25 – 9) = √16 = 4), come mostrato in Fig. 6.

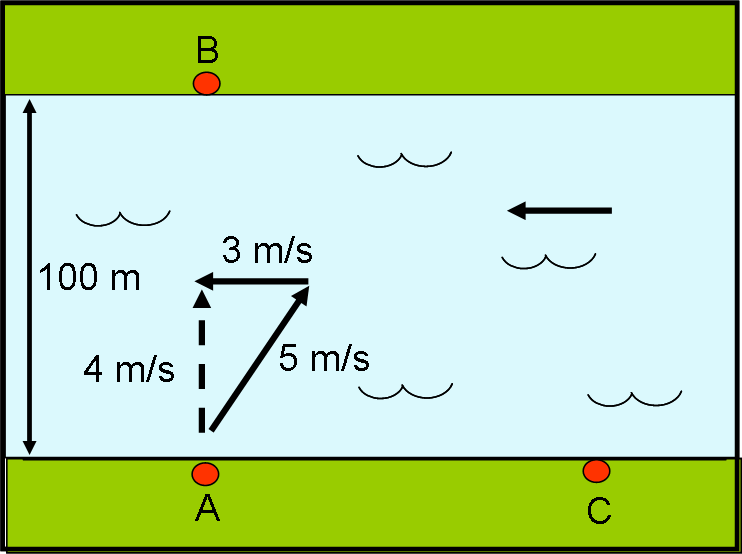
Ipotizzando un fiume largo 100 m, per raggiungere B il primo fotone impiegherebbe esattamente 25 secondi. Il ritorno sarebbe identico e quindi il traguardo sarebbe toccato dopo 50 secondi. Notiamo che il tempo impiegato sarebbe decisamente più lungo di quello ottenuto con il fiume fermo. In quel caso la velocità sarebbe sempre di 5 m/s e quindi l’andata e il ritorno si percorrerebbero entrambi in soli 100/5 = 20 secondi. Il tempo totale sarebbe di 40 secondi.

Vediamo, adesso, cosa succede al fotone che nuota lungo la sponda del fiume. Lui deve raggiungere C, andando in linea retta e alla velocità di 5 m/s, ma viene investito dalla corrente che cerca di trascinarlo indietro di 3 m/sec. In poche parole, in un secondo lui percorrerebbe 5 metri, ma sarebbe portato indietro di 3 metri. In conclusione, è proprio come se nuotasse a 5 – 3 = 2 m/s (Fig. 7a).

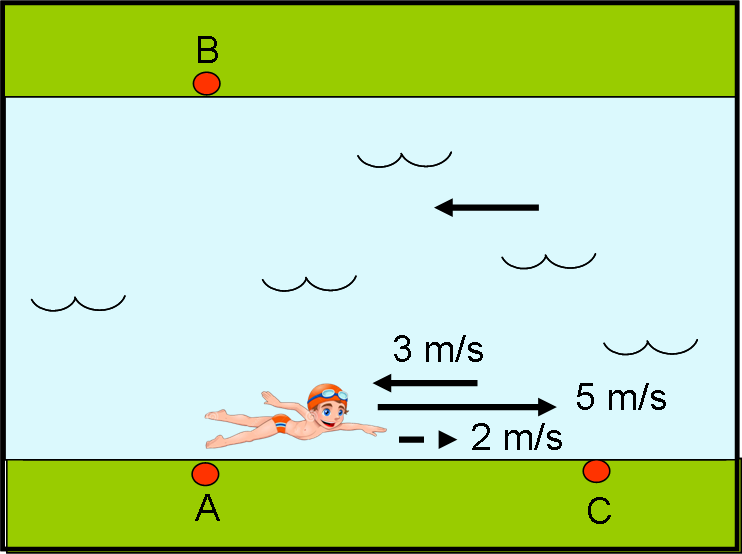
Per raggiungere C deve faticare molto e vi arriverebbe dolo 100/2 = 50 secondi (ricordiamo che la velocità si misura in metri diviso secondi, per cui dividendo i metri per la velocità si ottengono proprio i secondi impiegati).

Fortunatamente, il ritorno è decisamente più facile… Adesso, la corrente del fiume va nel verso del nuotatore e l’aiuta a spostarsi più velocemente. In un secondo il fotone percorrerebbe 5 metri, ai quali si aggiungono i 3 metri della corrente. Ne segue che il nuotatore si muove alla considerevole velocità di 5 + 3 = 8 m/s. I 100 metri del ritorno sarebbero, perciò, percorsi in solo 100/8 = 12.5 m/s (Fig. 7b).

Una vera saetta, ma… ormai è troppo tardi. Sommando i 50 dell’andata si ottiene un risultato finale di 50 + 12.5 = 62.5 secondi. Il secondo fotone arriverebbe al traguardo ben 12.5 secondi dopo l’arrivo del primo. Con pochi calcoli si potrebbe facilmente capire, da questo risultato, quanto vale la corrente del fiume, ossia quanto vale il vento dell’etere e - soprattutto - se esiste.

Parlando di velocità comparabili tra loro (3 e 5 metri al secondo), la gara avrebbe un netto vincitore e tutti i calcoli potrebbero essere fatti in modo banale. Ma, allora, perché dare un premio Nobel a un signore che ha inventato una gara così elementare e controllabile? Il fatto è che la differenza tra velocità del nuotatore e velocità della corrente del fiume è decisamente grande. I fotoni “nuotano” a 300 000 chilometri al secondo, mentre la Terra (e quindi il vento dell’etere) si muove a 30 chilometri al secondo. Il loro rapporto è 10 000, ossia i fotoni viaggiano 10 000 volte più veloci del vento dell’etere.

Questo fatto comporta una differenza tra i tempi impiegati dai due fotoni, praticamente impossibile da misurare ai tempi di Michelson (fine ottocento!).

Tuttavia, egli ebbe l’idea geniale che gli permise di ottenere il Nobel. Conoscendo bene i suoi due fotoni sapeva quanto velocemente riuscissero a saltellare sopra e sotto una linea diritta. Questi saltelli duravano pochissimo e tra il punto più alto di un saltello e quello del successivo saltello il tempo era dello stesso ordine della differenza di tempo impiegato dai due nuotatori. Guardando attentamente il punto A (di fine corsa) Michelson si sarebbe accorto che nell’istante in cui il primo fotone raggiungeva il punto più alto del saltello, il secondo sarebbe stato in ritardo e vicino al punto più basso. Questa differenza era facile da vedere e anche da fotografare. Una specie di fotofinish di una corsa ciclistica, analizzabile con molta calma e precisione.

Ovviamente, Michelson non usò un fiume, ma uno strano macchinario che mandava i fotoni in direzioni perpendicolari tra di loro, in modo da raggiungere una distanza uguale e tornare indietro. Ma il primo avrebbe subito il vento dell’etere come il nuotatore che ha attraversato il fiume; il secondo sarebbe andato nel verso del moto della Terra, ossia controcorrente nel fiume. Quest’ultimo sarebbe arrivato in ritardo di mezzo saltello circa! In tal modo, il nostro premio Nobel avrebbe potuto misurare, analizzando i saltelli (in parole tecniche la lunghezza d’onda), la velocità dell’etere, come fatto per la corrente del fiume (Fig. 8).

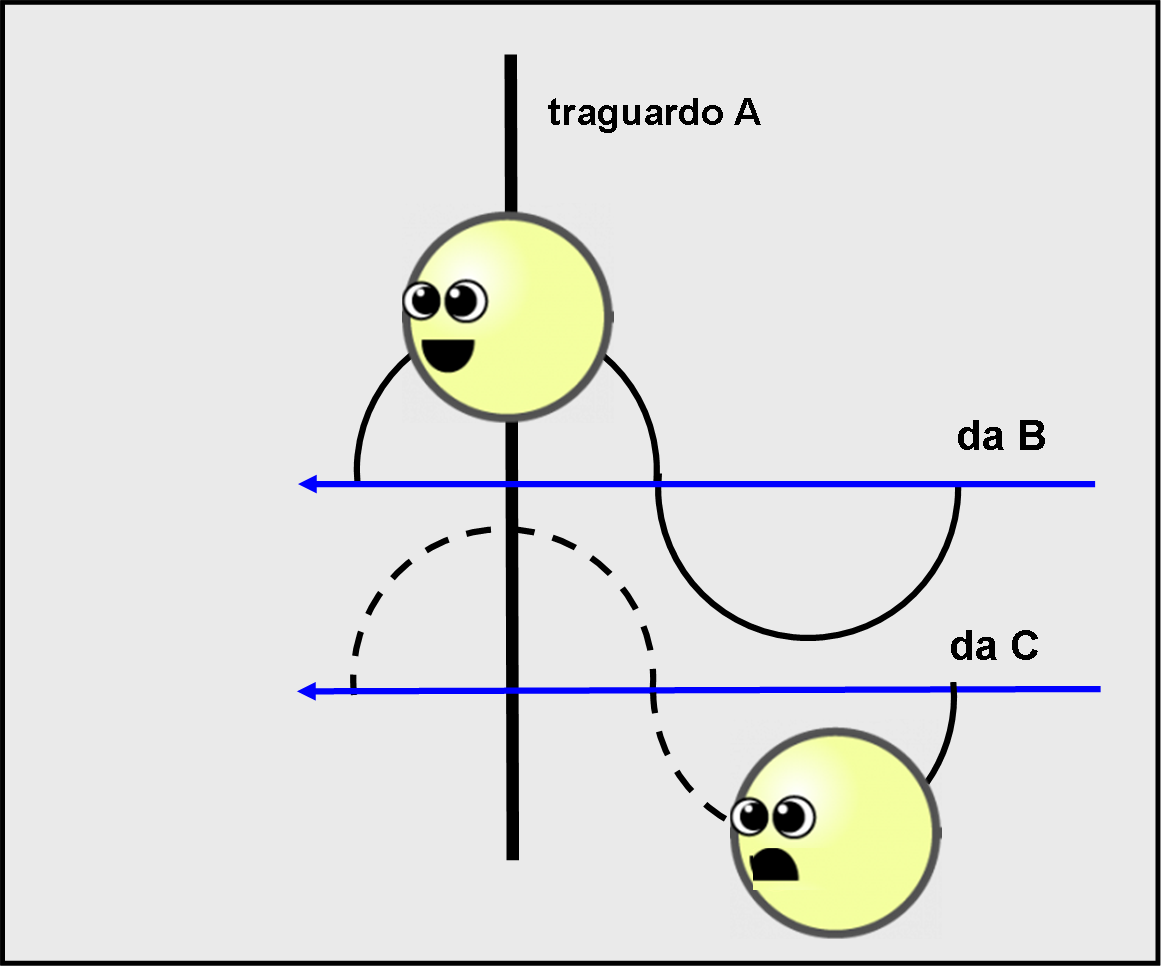
Più correttamente, i saltelli del secondo fotone sarebbero “sfasati” rispetto ai quelli del primo. Lo sfasamento, in realtà piccolissimo, si sarebbe, però, potuto misurare facilmente analizzando la luce che colpiva il traguardo, dove i due fotoni erano giunti.

Spieghiamoci meglio... Il secondo fotone arriva in ritardo rispetto al primo, ma la differenza di tempo è impossibile da misurare con un orologio. Tuttavia, in quella differenza di tempo così piccola, i fotoni sono capaci di effettuare almeno un saltello o poco meno. Ciò vuol dire che il secondo fotone arriva al traguardo dopo aver compiuto circa mezzo saltello in più (ha impiegato più tempo). La luce combinata dei due fotoni riesce a evidenziare questo sfasamento e valutare la differenza di tempo senza usare un orologio, ma solo attraverso lo sfasamento tra i saltelli. Invece del tic-tac dell'orologio si usa il rapidissimo tic-tac dei saltelli, molto più preciso e "facilmente" osservabile sulla linea del traguardo.

Tutto bene? Nemmeno per sogno! Compiendo l’esperimento nelle condizioni migliori a variando anche le direzioni dei due fotoni rispetto al moto della Terra (ossia della direzione del vento dell’etere) i due fotoni arrivavano sempre insieme al traguardo. Tutto succedeva come se non ci fosse corrente nel fiume, ossia come se la Terra non si muovesse. Dato, però, che la Terra si muove sicuramente, l’unica soluzione fu che non esisteva l’etere e quindi nemmeno il suo vento che favoriva o sfavoriva le due “nuotate”.

Un esperimento fallito, sicuramente, ma che permise di inventare un sistema per misurare differenze di tempo (e/o di metri) impossibili prima di allora. L’apparecchio di Michelson venne chiamato interferometro e si usa ancora adesso. Inoltre, la “scomparsa” dell’etere cambiò completamente la fisica dell’epoca, dimostrando che le onde luminose si propagano anche nel vuoto e che la velocità della luce resta sempre la stessa in qualsiasi sistema di riferimento si misuri: si era aperta la porta verso la relatività di Einstein.

Ma questa è tutta un’altra favola…

Parliamo più seriamente...

Dopo la favola  non ci rimane che spiegare l’esperimento di Michelson e Morley in maniera un po’ più scientifica, utilizzando (poca) matematica e geometria.

Qualche considerazione preliminare

Non sono pochi quelli che credono che il Nobel sia stato dato all’esperimento e alle sue conclusioni, trovando ciò poco onesto, in quanto il risultato è stato, in realtà, un completo fallimento. A parte il fatto che dimostrare che non c’è bisogno di etere per trasportare le onde elettromagnetiche sarebbe già un risultato non da poco, il Nobel è stato dato SOLO a Michelson (e non a Morley che aveva collaborato alla pari nell’esperimento, portando migliorie decisive) per il metodo che aveva ideato. Utilizzare il fenomeno dell’interferenza luminosa (QUI e QUI) per misurare differenze di percorso (meglio dire “cammino ottico”) o di tempo, ben al di sotto delle possibilità degli strumenti tradizionali, ha aperto le porte a una tecnologia eccezionale, che ancora oggi viene usata in mille e una situazione. Nobel all’interferometro, perciò, e non alla scomparsa dell’etere.

Un minimo di storia

La teoria ondulatoria della luce è generalmente fatta risalire a Huygens, tra il 1678 e il 1690. Egli non poteva che assumere un’analogia fra la luce e il suono e, quindi, non poteva fare altro che pensare all’esistenza di una certa “materia” tra la sorgente della luce e l’osservatore. Non potendo certo essere lo spostamento della materia a trasportare la luce, essa, come il suono, doveva consistere in oscillazioni che si propagavano in un mezzo materiale. Nel 1802 Young ipotizzò “un etere luminifero, rarefatto ed elastico: tutte le volte che un corpo emette luce, vengono eccitate delle onde nell’etere”.

Nacque così il concetto di un etere trasportatore della luce, simile a un fluido rarefatto, elastico, senza peso, presente in tutto l'Universo. Nel 1804, ancora Young sosteneva: “... Sono disposto a credere che l'etere luminifero pervada la sostanza di tutti i corpi materiali, con resistenza piccola o nulla, forse liberamente, come il vento passa attraverso un boschetto di alberi …”

Nel frattempo, il genio di Maxwell operava la sintesi dell’elettromagnetismo, dimostrando che sia le azioni elettriche che quelle magnetiche si propagavano come onde di velocità uguale a quella della luce visibile, che ne era, quindi, un caso del tutto particolare.

L'etere diventava così la base fondamentale per le azioni elettriche e magnetiche. Qualunque cosa fosse, doveva pervadere tutto lo spazio. Lo stesso Maxwell nel 1878 scriveva: "Qualunque difficoltà possiamo avere nel formare un'idea consistente della costituzione dell'etere, non ci può essere dubbio che gli spazi interplanetari e interstellari non siano vuoti, ma siano occupati da una sostanza materiale o corpo, che è certamente il più grande e probabilmente il corpo più uniforme fra quelli di cui abbiamo qualche conoscenza.”

Ma l’etere era fermo o si muoveva? Diverse erano le ipotesi… secondo alcuni, i corpi celesti potevano trascinare l'etere con sé nel loro moto in prossimità della superficie (come una specie di atmosfera). Secondo altri lo potevano fare, parzialmente, solo corpi dotati di particolari proprietà ottiche (come quelli trasparenti). Oppure, come diceva Lorentz, l'etere era a riposo. In quest'ultima ipotesi, la velocità della luce che era c rispetto all'etere, rispetto a un altro corpo in moto con velocità v nell'etere, doveva essere c +/- v, con grande soddisfazione di Galileo Galilei.

Esperimenti condotti sulla Terra con sorgenti di luce terrestri avrebbero dovuto mettere in evidenza tale cambiamento di velocità. Questo fatto equivaleva ad ammettere che, almeno per i fenomeni elettromagnetici e ottici, l'etere costituiva un riferimento assoluto. La velocità della luce con sorgenti terrestri fu proprio determinata in questo modo (ne parleremo più tardi), utilizzando esperimenti in cui la luce percorreva una certa distanza sia in un verso che nell’altro. Lo stesso percorso rettilineo eseguito all’andata e al ritorno permetteva di fare la media, trascurando i termini di secondo grado in v/c.

Infatti, se d è la lunghezza del percorso, si ha che il tempo totale, tra andata e ritorno, vale:

t = d/(c + v) + d/(c – v) = d(1/(c + v) + 1/(c – v)) = d(c + v + c – v)/(c² – v²)

t = 2d c/(c² – v²)

Misurato il tempo, basta dividere la lunghezza totale del percorso (andata e ritorno) per il tempo e si ottiene la velocità della luce a meno di un fattore del second’ordine in v/c, che può essere trascurato:

2d/t = c/(c² – v²) = c (1 – v²/c²) ≈ c

Maxwell osservava: “Se fosse possibile determinare la velocità della luce, osservando il tempo che impiega per viaggiare tra una stazione e un'altra sulla superficie della Terra, potremmo, confrontando le velocità osservate in direzioni opposte, determinare la velocità dell'etere rispetto a queste stazioni terrestri. Però tutti i metodi con cui è possibile determinare la velocità della luce da esperimenti terrestri dipendono dalla misura del tempo richiesto per il doppio cammino da una stazione all'altra e ritorno, e l'aumento di questo tempo .... sarebbe non rilevabile”.  In poche parole, bisognava essere in grado di evidenziare grandezze dell’ordine di (v/c)².

Questo è stato il problema che Michelson decise di affrontare nel 1881 (in modo troppo “rozzo”) e nel 1887 insieme a Morley.  Doveva evidenziare la differenza di velocità della luce dovuta al moto della Terra attraverso l'etere, cioè provare sperimentalmente l'ipotesi dell'etere a riposo, data per certa la sua esistenza.  Per far ciò, come già detto, doveva usare un metodo sensibile a una variazione del secondo ordine di v/c. E questo metodo non poteva basarsi certo su misure dirette.

Nel 1881 disse: “La teoria ondulatoria della luce assume l'esistenza di un mezzo chiamato etere, le cui vibrazioni producono i fenomeni della luce, e che è supposto riempire tutto lo spazio… Assumendo che l'etere è a riposo, mentre la Terra si muove attraverso di esso, il tempo richiesto perché la luce passi da un punto all'altro della superficie della Terra, dipenderebbe dalla direzione in cui viaggia”. Poi proseguì, ricordando le asserzioni di Maxwell: “Fino ad ora non avevamo alcun metodo per misurare la velocità della luce che non comprendesse la necessità di far ritornare la luce sul suo cammino, per il quale motivo essa perderebbe circa tanto quanto ha guadagnato nell'andata. Poiché la differenza dipende dal quadrato del rapporto fra le due velocità, secondo Maxwell, è troppo piccola per essere misurata”.

L'idea geniale di Michelson fu di ricorrere all’utilizzo della lunghezza d’onda della luce come unità di misura, valutando i tempi attraverso la variazione di fase osservata al punto di arrivo. In altre parole, usò il fenomeno dell'interferenza, che permetteva di misurare senza problemi gli effetti del secondo ordine in v/c attraverso lo spostamento delle frange di interferenza, in funzione del cammino ottico.

Ritardare la luce

L’idea di base era quella di inviare due raggi luminosi in direzioni perpendicolari tra loro che coprissero un percorso uguale. Essi si sarebbero mossi con velocità c. Tuttavia, il raggio che si muoveva nella stessa direzione della Terra attorno al Sole avrebbe dovuto "nuotare" lungo il vento dell’etere, una volta in moto contrario e una volta a favore, mentre il raggio a 90° l’avrebbe attraversato sempre avendolo perpendicolare.

Spieghiamoci meglio. Se l’etere esisteva ed era fermo rispetto alla Terra, chi si muoveva con la Terra doveva subire un vento di etere di intensità uguale e opposta al moto della Terra. Ossia, il vento dell’etere si doveva muovere con velocità –v. All’andata, al pari del nuotatore della favola, la luce avrebbe trovato un ostacolo nel propagarsi, mentre al ritorno avrebbe avuto un aiuto. In ogni caso il tempo totale  sarebbe stato maggiore di quello del “nuotatore” perpendicolare. Un cammino ottico più lungo avrebbe provocato uno sfasamento nell’onda luminosa, perfettamente misurabile attraverso il fenomeno dell’interferenza. Un’idea geniale e rivoluzionaria!

Qualche calcolo facile facile

La Fig. 9 mostra lo schema dell’esperimento.

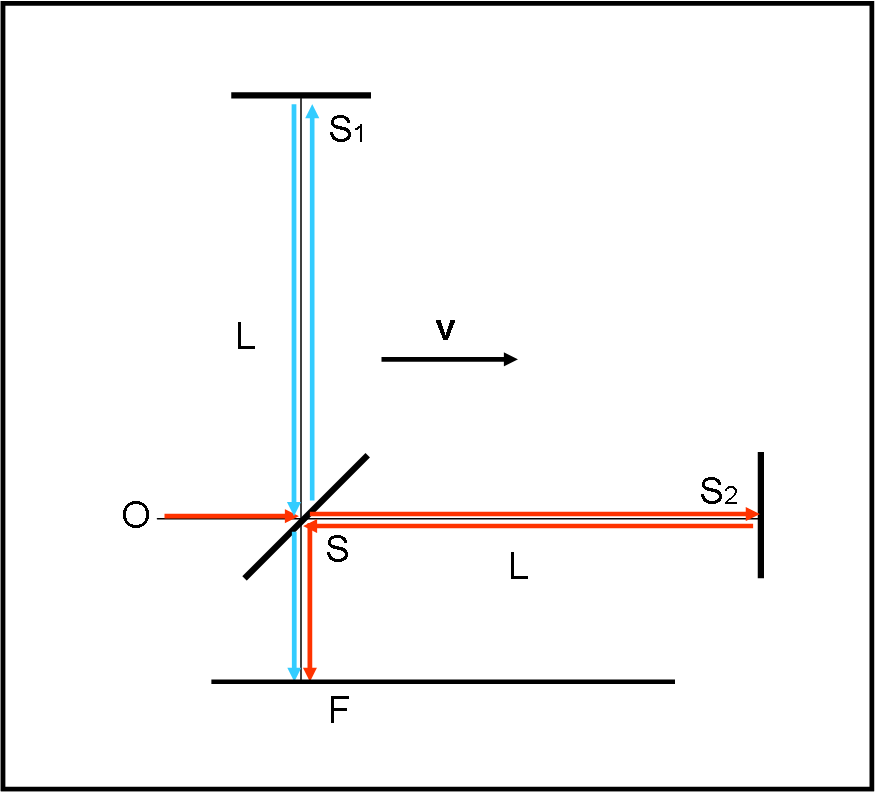
La luce parte da O e si dirige, nel verso del moto terrestre, fino a uno specchietto S inclinato di 45°, che permette al raggio di riflettersi e di attraversarlo (specchio semiriflettente). Il raggio, ancora perfettamente in fase, si sdoppia. Una parte di esso (quello blu, riflesso) si dirige verso S₁, specchio completamente riflettente, e torna indietro. Incontra nuovamente S, lo attraversa e va a formare l’immagine in F.

Il secondo raggio (rosso) prosegue verso S₂, un altro specchio riflettente, e torna indietro fino a S. Si riflette e si dirige verso F.

Aver colorato in rosso e blu i due raggi è solo di aiuto al disegno, in quanto la luce inviata non cambia la propria lunghezza d’onda lungo il percorso. Nel calcolo dei tempi impiegati dai raggi non si considerano quelli relativi al tratto OS e SF, dato che sono perfettamente identici tra loro. Ci limitiamo, quindi, solo alla parte SS₁S e SS₂S. Le distanze SS₁ e SS₂ sono uguali e valgono L (ma poco cambierebbe concettualmente anche se fossero diverse).

Cominciamo con il raggio rosso. Il tempo impiegato tra andata e ritorno da S a S₁, e viceversa, sembrerebbe veramente banale da scrivere:

t₁ = 2 L/c

Vedremo tra poco che questa relazione, usata subito da Michelson, non è esatta e fu corretta solo in seguito.

Passiamo, momentaneamente, al raggio blu che attraversa, all’andata, lo specchio S e percorre la  lunghezza L fino ad arrivare a S₂, dove viene riflesso. In questo caso, dobbiamo fare entrare in azione il vento dell’etere. All’andata la velocità è data da c – v, mentre al ritorno è data da c + v (come abbiamo già visto precedentemente):

t_2A= L(c – v)

t_2R= L(c + v)

t₂ = L/(c – v) + L/(c – v)

maneggiando un po’ la formula, come già fatto all’inizio, si ottiene:

t₂ = 2L/(c² – v²) = 2L/(c (1- v²/c²)) = 2Lγ²/c          …. (1)

ponendo (guarda caso…)

γ = 1/(1- v²/c²)^1/2

Ci fermassimo qui, potremmo dire facilmente che t₂ > t₁. Tuttavia, non possiamo dimenticare il fatto che t₁ è SBAGLIATO. La ragione sta nel fatto che lo specchio S si muove con la Terra (qualcosa di simile all’orologio di luce, visto nella relatività ristretta) alla velocità v,  e il raggio che va da S a S₁ è costretto a muoversi “in diagonale” sia all’andata che al ritorno. Per calcolare esattamente il tempo t₁, bisogna, allora, fare intervenire il teorema di Pitagora e guardare la Fig. 10.

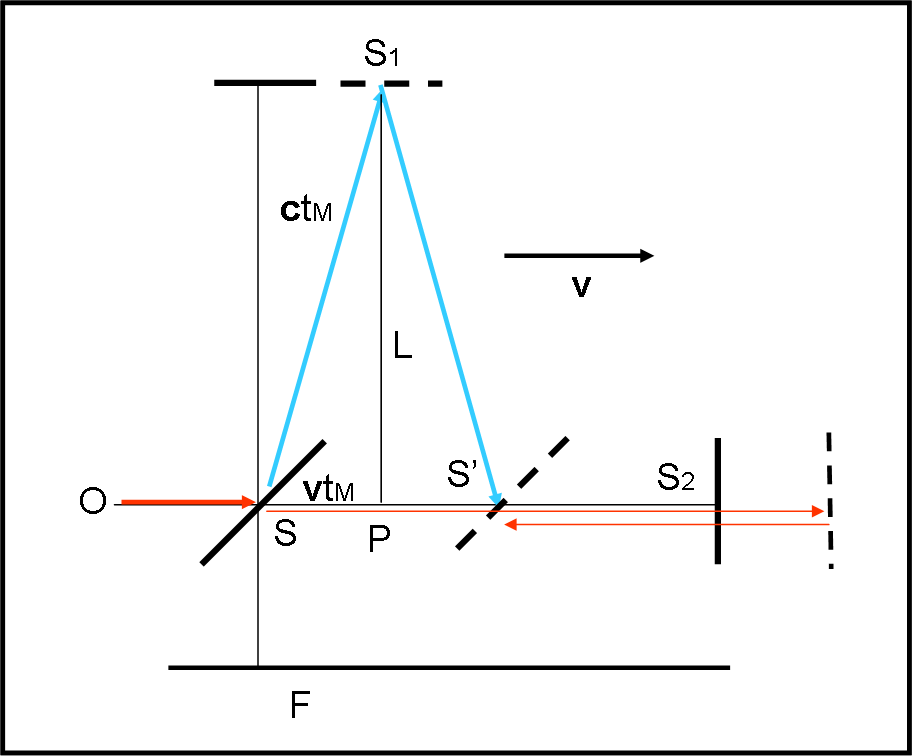
Si ha subito che il tempo totale t₁ è dato dalla somma del tempo impiegato per arrivare da S a S1 e di quello impiegato per andare da S1 a S’ (posizione finale dello specchio S). Ma i due tempi sono uguali (la stessa cosa che capitava per il nuotatore che attraversava il fiume) e quindi il tempo totale t₁ è il doppio del tempo impiegato per andare da S a S1. In poche parole, calcoliamo t_M, il tempo impiegato per andare da S a S₁, e poi lo raddoppiamo. Per fare ciò basta applicare il teorema di Pitagora al triangolo SS₁P.

SS₁² = SP² + L²

c²t_M² = v²t_M² + L²

t_M² = L²/(c² – v²)

t_M = L/(c² – v²)^1/2

t₁ = 2t_M = 2L/(c² – v²)^1/2

t₁ = 2L/c (1 – v²/c²)^1/2

t₁ = 2Lγ/c                                   …. (2)

E’ immediato notare che t₁ risulta sempre minore di t₂ e quindi i tempi impiegati dai due raggi sono decisamente differenti (anche se per quantità dell’ordine di v²/c^2.).

Facciamo la differenza tra i due tempi, ossia facciamo la differenza tra la (1) e la (2):

t₂ – t₁ = 2Lγ²/c - 2Lγ/c               …. (3)

La strumentazione poteva essere ruotata, in modo che il braccio diretto verso il moto della Terra si venisse a trovare a 90° rispetto a prima e i tempi si sarebbero invertiti. In tale modo si otteneva uno sfasamento doppio. Moltiplicando per c si aveva la differenza di cammino ottico nei due casi.

Δ₀ = 2Lγ² - 2Lγ

Δ₉₀ = 2Lγ - 2Lγ²

Dividendo la loro differenza per la lunghezza d’onda usata (giallo), si ricavava lo spostamento n delle frange di interferenza (assumendo, come già detto, un etere fermo rispetto alla Terra).

n = (Δ₀ - Δ₉₀)/λ

Nell’esperimento, la lunghezza L era di 11 metri (facendo andare avanti e indietro la luce  parecchie volte), mentre λ era di circa 500 nm.

Ne risultava uno spostamento atteso delle frange di 0.44. Un qualcosa di estremamente ben visibile!

E, invece, niente! Come spiegare il fallimento?

Si cercò di darne una spiegazione, ma risultò estremamente difficile. Si poteva dire che l’etere si muoveva con la Terra, ma in questo caso si sarebbe andati contro l’aberrazione della luce. Si tentò anche con qualche via di mezzo, ma le spiegazioni risultavano prive di senso fisico. Una spiegazione più valida venne data da Fitzgerald (1889) e da Lorentz (1892), ipotizzando che le distanze si contraessero nel verso del moto. Questa contrazione la conosciamo molto bene ed è data dal fattore γ. In parole più tecniche, la lunghezza nel verso del moto terrestre sarebbe diventata:

L_c = L/γ

In verità, se andiamo a sostituire L_c al valore di L, per il tragitto nel verso del moto, la (3) diventa:

t₂ – t₁ = 2L_cγ²/c - 2Lγ/c = 2Lγ/c - 2Lγ/c = 0

Lo spostamento delle frange si annullerebbe!

Questa ipotesi si basava sul fatto che i campi elettrostatici si deformano quando erano in movimento. Tuttavia, a quei tempi, questa spiegazione apparve subito come una soluzione  “ad hoc”, non basata su conoscenze fisiche accettabili (poco si sapeva delle forze intermolecolari). Solo Einstein, nel 1905, riuscì a distruggere questa critica, dimostrando che non vi era alcuna necessità di muoversi attraverso l’etere per avere una contrazione delle lunghezze. Bastava cambiare completamente le idee di spazio, tempo, simultaneità e descrivere la relatività ristretta, assumendo una velocità della luce costante in ogni sistema di riferimento!

Einstein distrusse l’etere e, quindi, in particolare, l’essenza fisica della contrazione. Un fenomeno dovuto solamente al sistema di riferimento. Tuttavia, come già detto altrove, l’esclusione di un mezzo che permeava tutto l’Universo non lo soddisfaceva del tutto: all’etere, in pratica, sostituì il concetto di campo, le cui equazioni descrivono lo spaziotempo attraverso la relatività generale. In qualche modo, questo concetto riporta la contrazione verso un significato nuovamente fisico.

Misurare la velocità della luce

Abbiamo visto come la velocità della luce non si sommi o si sottragga ad altre velocità, in disaccordo con quanto detto da Galileo. Ovviamente, Galileo non poteva calcolare la velocità della luce con esperimenti terrestri, essendo troppo alta, e quindi i tempi impiegati a percorrere brevi tragitti del tutto fuori portata (come vedremo tra poco). Lo stesso Michelson ha dovuto inventarsi un esperimento geniale che si basasse sull'interferenza. Tuttavia, la scoperta del telescopio permise di misurare, in modo abbastanza preciso, la velocità della luce ben prima degli esperimenti terrestri.

I metodi astronomici

Fin dai tempi più antichi ci si è sempre chiesti se la luce avesse una sua velocità o si propagasse istantaneamente. Sapendo, oggi, che essa si aggira intorno ai 300 000 km/s, risulta ovvio che nessuno avrebbe potuto rispondere, con le informazioni che si potevano ottenere sul nostro pianeta, troppo piccolo per permettere misure oltre ai limiti di una tecnologia ancora troppo rozza.

Il grande Galileo si era fatto quella domanda e aveva già intuito che la questione era ancora lontano dal potere essere risolta, dopo aver fatto tentativi ai limiti delle possibilità di quei tempi: orologi molto approssimativi e distanze troppo corte. Ne avevamo già parlato, ma ricordiamo, comunque, che aveva mandato un suo assistente su una collina piuttosto distante dalla sua, con una lampada in mano (o meglio torcia o qualcosa di simile). Galileo aveva acceso la sua torcia al tempo t₁, il suo assistente, una volta vista la luce, aveva mostrato la sua torcia (al tempo t₂) e infine Galileo aveva segnato il tempo t_3, in cui aveva ricevuto la luce dell’assistente. Malgrado avessero anche cercato di allungare il percorso con degli specchi, il risultato non poté che essere negativo.

Infatti, la velocità della luce avrebbe dovuta essere calcolata dividendo la doppia distanza 2d, tra Galileo e l’assistente,  per la differenza di tempo t₃ – t₁. Oggi ci viene da ridere, dato che t₃ – t₁ era troppo piccolo per essere misurato da orologi ancora primitivi (ma lo sarebbe tutt’ora) e quindi il risultato non poteva che essere: velocità infinta (d/0 => ∞)!

Tuttavia, Galileo aveva capito che il valore poteva benissimo essere finito, ma che per il momento non si poteva che accettare una velocità infinita, ossia assumere che la luce si propagasse in un tempo trascurabile a tutti gli effetti.

In altre parole, la Terra era troppo piccola per fornire distanze tali da accettare gli errori sui tempi e ottenere una velocità in qualche modo approssimata, ma sensata. Ci sarebbe voluto un assistente posto al di fuori del nostro pianeta o, quantomeno, un specchio molto, molto lontano, che inviasse indietro il raggio luminoso, permettendo che passasse un tempo, tra partenza e arrivo, abbastanza lungo.

Fu proprio Galileo a fornire la prima possibilità di misura della velocità della luce, attraverso la  scoperta del telescopio e dei satelliti medicei. Lui non ci pensò (probabilmente), ma aveva proprio “creato” la sorgente lontana, a distanza conosciuta, che poteva inviare il segnale luminoso!

Roemer e il satellite Io

I satelliti di Giove furono osservati a lungo negli anni successivi alla loro scoperta e così anche le eclissi dei suoi satelliti. Cassini eseguì osservazioni meravigliose a riguardo. Un astronomo olandese, Olaus Roemer, analizzò a lungo queste osservazioni e si accorse che qualche cosa non andava per il suo verso. Si poteva dire di conoscere abbastanza bene l’orbita terrestre e le orbite dei satelliti attorno a Giove e niente avrebbe potuto cambiarle (ipotesi più che valida per quei tempi). Ragione per cui l’ingresso dei satelliti nell’ombra di Giove, nelle varie configurazioni geometriche, doveva avvenire in istanti calcolabili abbastanza facilmente con la precisione degli orologi. E, invece, si trovavano differenze troppo elevate.

In particolare, più la Terra si avvicinava a Giove e più i tempi di ingresso nell’ombra anticipavano. L’esatto contrario, quando la Terra si allontanava (osservando, ad esempio, l’uscita dall’ombra). La Fig. 11 mostra bene la situazione per il satellite Io. Mentre la Terra passa da T1 a T2 gli ingressi anticipano; quando passa da T3 a T4 le uscite ritardano. Roemer, in realtà, valutava la durata dell’intera eclissi e trovava una sua durata variabile. Il succo del discorso è, però, esattamente lo stesso.

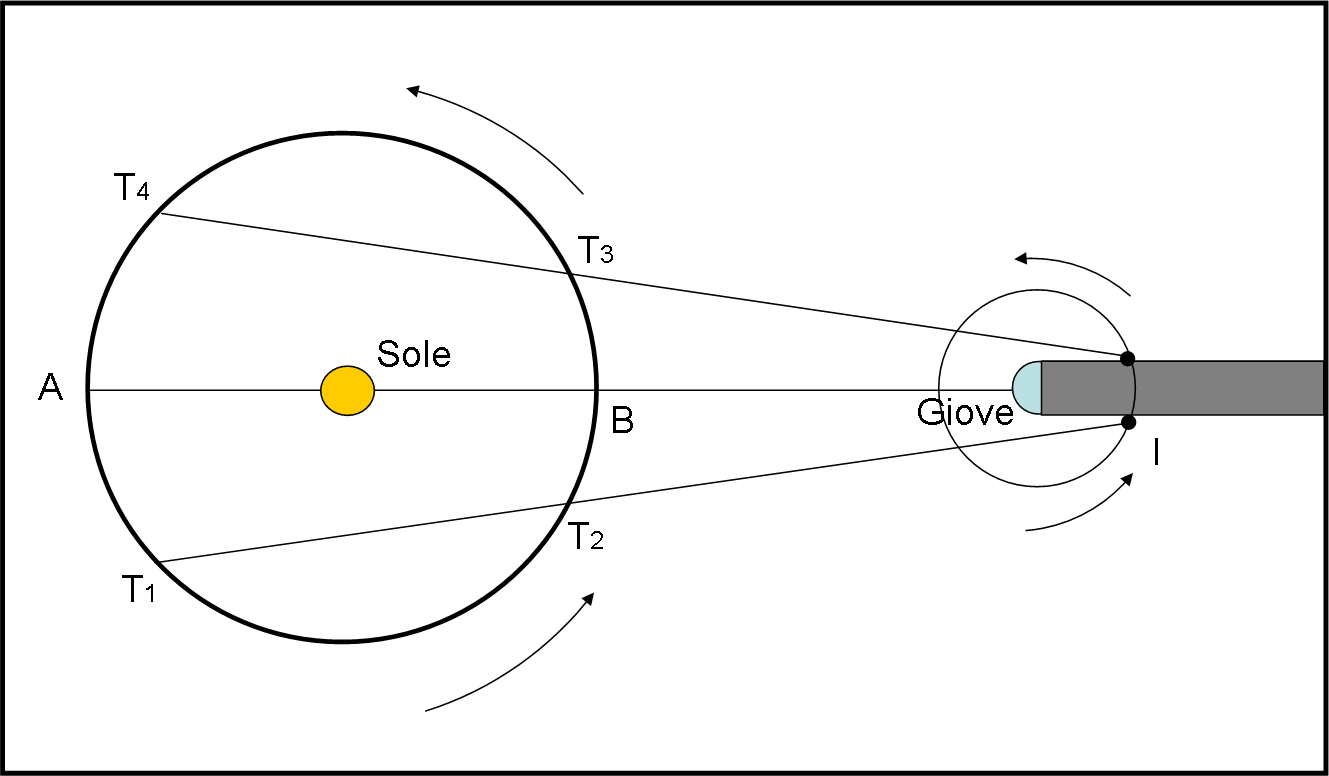
Come sempre, per le idee geniali, oggi sembrerebbe che ci volesse ben poco a capire che queste variazioni così regolari fossero dovute alla variazione della distanza tra la Terra e Giove o -meglio- alla distanza tra Io e la Terra, ma dobbiamo ricordare che molti colleghi scienziati di Roemer, anche prestigiosi, erano ancora convinti (seguendo Aristotele) che la luce dovesse propagarsi istantaneamente. I preconcetti sono duri a morire e certe conclusioni contro la credenza collettiva sono sempre atti di coraggio (rogo o non rogo).

Attraverso molte osservazioni, Roemer riuscì a riportare il problema a un semplicissimo schema, che introduceva le distanze di Giove misurata da A e da B e legava a loro le differenze di tempo tra due ingressi di Io nell’ombra. In semplicissime parole matematiche:

velocità luce = (A_I – B_I)/(t_A – t_B) = 2a/dt = c

Dove 2a è il diametro dell’orbita terrestre e dt la differenza di tempo massima calcolata attraverso molte osservazioni. La c che è stata associata alla velocità della luce viene dal latino “celeritas”.

Purtroppo, ai tempi di Roemer, la distanza Terra-Sole era conosciuta con grande imprecisione, così come vi era un errore ancora sensibile nella differenza dei tempi (dell'ordine dei venti minuti). Ne segue che il valore dedotto dal grande olandese nel 1676 fu di solo 210 000 km/s. Molto meno del valore reale, ma il concetto era giusto e a fine settecento si ottenne già un valore ben più preciso, pari a 310 000 km/s.

Galileo aveva ragione e la luce diventava una grandezza fisica a tutti gli effetti.

Bradley e l'aberrazione annua

Non era ancora passato mezzo secolo dalla determinazione di Roemer, che Bradley, nella continua ricerca di misurare la parallasse stellare, si convinse di esserci riuscito, osservando la stella gamma del Dragone. Il valore trovato fu di 20.5”. Veramente grande… troppo grande (la stella sarebbe stata troppo vicina!). Ma, ancor peggio, Bradley si accorse che anche le altre stelle mostravano la stessa parallasse annua. In poche parole non aveva misurato la parallasse, ma l’aberrazione annua, una scoperta estremamente importante per vari motivi.

Non voglio entrare nei dettagli, dato che l’abbiamo trattata molto attentamente in questo approfondimento.  Un approfondimento che è molto interessante non solo per la determinazione di c. In qualche modo, sto cercando di invogliarvi ad andare a rileggerlo, se non lo avete già fatto. Poi, quanto diremo di seguito, diventerà cosa più che banale.

Resta il fatto che l’angolo “apparente” sotto cui si vede una stella differisce da quello “vero” a causa della combinazione della direzione da cui proviene la luce e la direzione verso cui si sta muovendo la Terra nella sua orbita attorno al Sole. In altre parole, l’angolo dipende dal rapporto tra velocità della luce e velocità orbitale (La Fig. 12 riporta il concetto base dell’aberrazione).

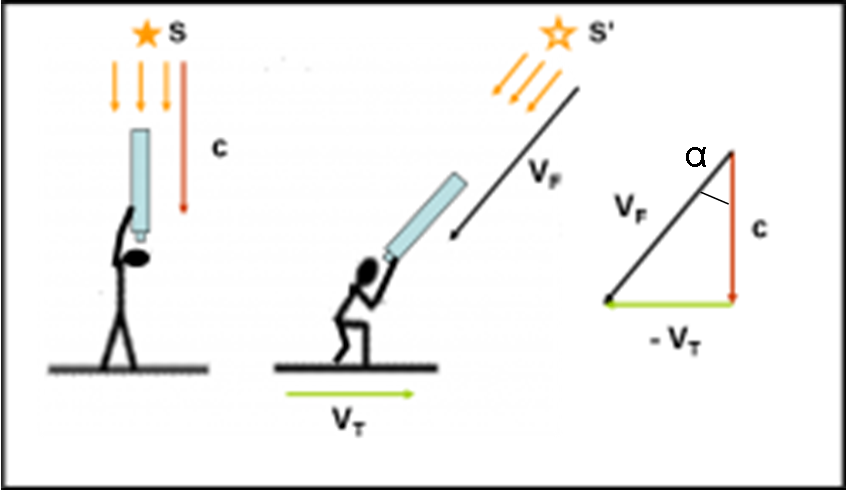
L’angolo α di aberrazione si misurava attraverso le osservazioni e la velocità della Terra era nota (30 km/sec). Ne seguiva immediatamente il valore di c, che risultò essere

c = 301 000 km/s

Una piccola-grande conseguenza dell’aberrazione annua, che riguarda più da vicino l’esperimento di Michelson e Morley (descritto all'inizio): se l’etere fosse stato a riposo rispetto alla Terra, esso si sarebbe mosso insieme a lei con la stessa velocità. Ma, in questo caso, anche il raggio di luce sarebbe stato trascinato insieme all’etere e l’aberrazione non avrebbe dovuto esistere. Questo fatto implicava, perciò, un etere fisso rispetto al moto del nostro pianeta e, di conseguenza, l’ipotesi di un vento dell’etere era più che accettabile.

Un manoscritto sconosciuto di Archimede

Prima di passare ai metodi "terrestri", divertiamoci un po' con una fantastoria (ma chissà...), che ci permette di avvicinarci a un certo Sig. Fizeau...

Le grandi scoperte si fanno anche passando ore e ore in vecchie e sconosciute biblioteche. E così sembra che sia saltato fuori addirittura un manoscritto di Archimede che descrive un esperimento che ha del favoloso! Purtroppo, il documento preziosissimo è molto rovinato. Vogliamo provare a ricostruirlo con le nostre conoscenze?  Altro che Galileo Galilei, le sue lampade e il povero assistente sperduto sui colli toscani…

Sembra che il grande scienziato greco fosse già stato in grado di ottenere un valore approssimato della velocità della luce. Come già detto, il manoscritto è molto rovinato, ma pare che siano stati necessari due soldati gemelli, come quelli della figura che segue, e una biga tirata da 4 velocissimi cavalli, estremamente regolari nella corsa (forse imparentati con il dromedario di Eratostene…). Una figura semi cancellata raffigura, addirittura, un cavallo alato... forse Pegaso?

Ovviamente Archimede ha anche utilizzato uno dei suoi attrezzi più famosi, lo specchio!

Cerchiamo di ricavare il metodo possibilmente usato dallo scienziato greco e, alla fine, di concludere se  il manoscritto è autentico o è solo una bufala estremamente ben preparata.

Vediamo cosa avrebbe fatto Archimede… fermo restando che sono ammesse alcune varianti. L’importante è il concetto di fondo e la velocità di Pegaso & co.

Innanzitutto, pone uno specchio piano a una distanza di 10 km dalla sua posizione di misura. Di specchi ne aveva a iosa e per lui era uno scherzo farne uno anche piuttosto grande. Lo specchio era, ovviamente, sistemato perpendicolarmente alla linea immaginaria che lo univa allo scienziato. Per misurare la distanza, sembra che Archimede abbia veramente usato un dromedario, stretto parente di quello di Eratostene.

La misura sarebbe stata fatta quando il Sole era perfettamente alle spalle di Archimede, sulla stella linea Archimede-specchio. Sembra che una configurazione di questo tipo sia stata ottenuta aggiungendo un po’ di specchi (anche se non necessari, ma Archy era un vero fanatico…) e un diaframma che limitasse le dimensioni del Sole, riducendolo a un punto luminoso.

In poche parole, Archimede, specchio e Sole erano piazzati come in Figura 13.

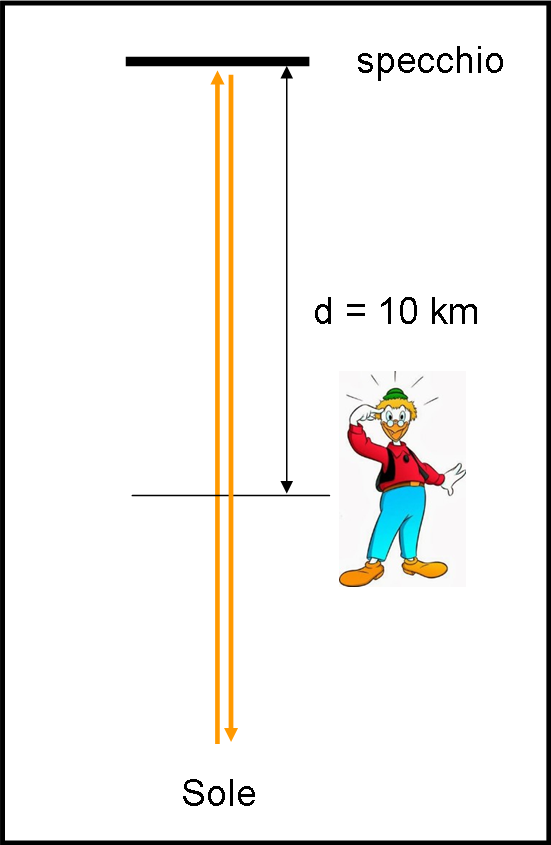
I raggi solari, molto limitati, sarebbero tornati perfettamente indietro fino a raggiungere nuovamente Archimede. Se chiamiamo c (celeritas) la velocità della luce, vale la relazione:

t_R – t_A = 2d/c

con t_R e t_A i  tempi di partenza e di ritorno della luce da Archimede

Archimede aveva a disposizione solo clessidre e orologi ben poco precisi e, di conseguenza, sapeva benissimo di non poter misurare il tempo in cui la luce avrebbe percorso il tratto Archimede-specchio più quello di ritorno specchio-Archimede (la stessa conclusione di Galileo). Infatti, oggi sappiamo bene che la velocità della luce vale circa 300 000 km/s. Il che vuole dire che avrebbe percorso 2·10 = 20 km in un tempo pari a:

t_R – t_A = 20/300 000 = 0.0001 secondi (circa)

qualcosa di impensabile anche per una clessidra di precisione (ma anche per i nostri orologi da polso…).

Era, quindi, necessario fare sparire il tempo dalla misura. Per ottenere ciò doveva far svolgere nello stesso tempo una qualche altra azione, più facilmente misurabile.

Ed ecco, allora, chiamare in soccorso il cavallo Pegaso (gli deve essere costato una bella cifra!) con tre amici della stessa forza fisica. Si sapeva che la velocità dei quattro cavalli avrebbe raggiunto i 540 km/h, anche trasportando un peso non indifferente. Descriviamo, allora, qual è questo “peso” supplementare: una biga e due soldati muniti di due scudi lavorati in modo perfetto. I loro bordi erano lisci e dritti come pochi, sicuramente spaccavano il millimetro e anche meno.

Il sistema cavalli-biga-soldati con lo scudo avrebbe dovuto passare a grande velocità davanti ad Archimede, in direzione perpendicolare alla congiungente Sole-specchio, come mostrato schematicamente in Fig. 14. Nella figura non si sono disegnati i due soldati che si sono nascosti abilmente dietro ai propri scudi.

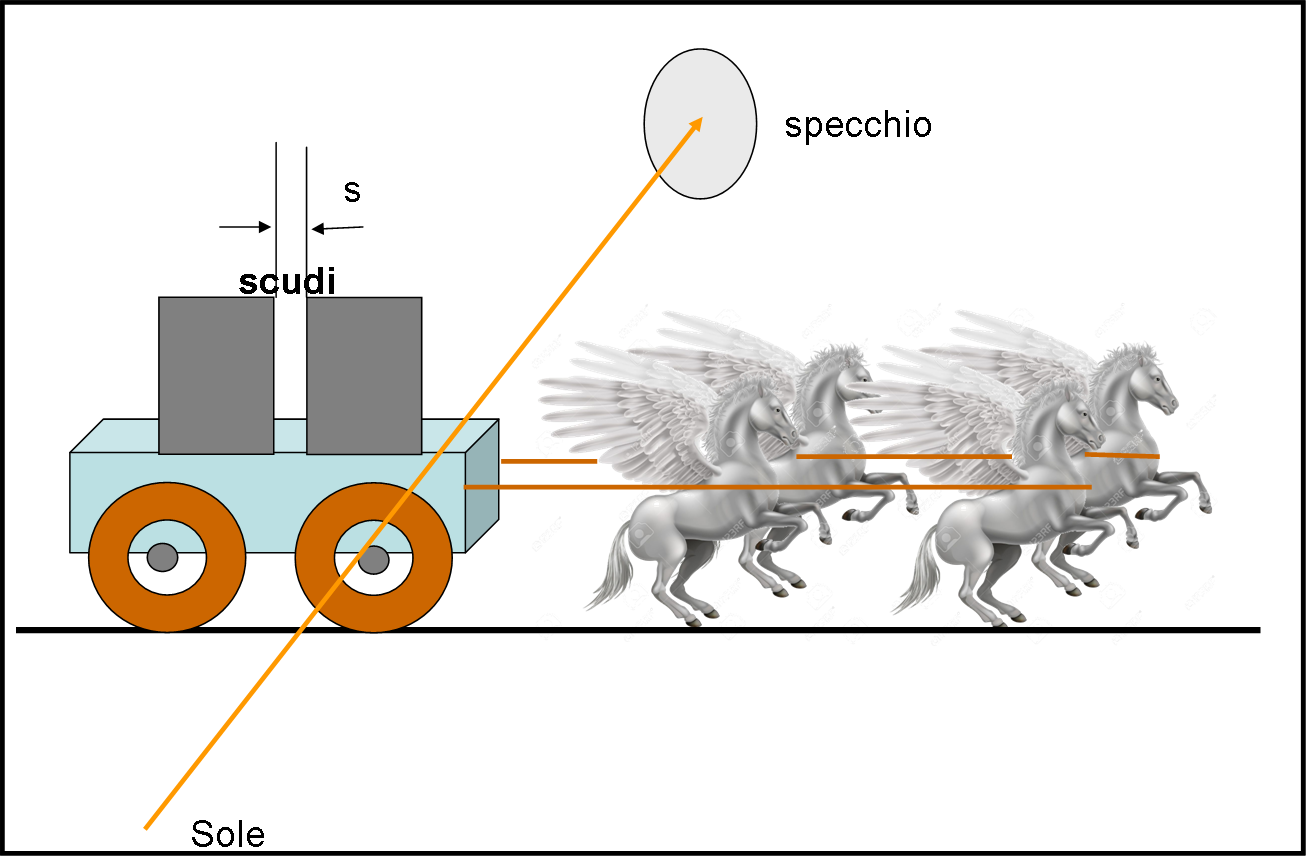
Adesso, le cose si complicano un pochino, ma Archimede era o non era un genio? Lui ragiona e pensa: “Se la luce solare incontra uno scudo non riesce a raggiungere lo specchio e io, guardando in quella direzione, non vedrò nulla. Se, invece, la luce passa tra uno scudo e l’altro, vedrò il riflesso del Sole causato dallo specchio. Devo fare in modo di mettere i due scudi a una distanza, l’uno dall’altro, tale che, mentre i cavalli sono al galoppo, sia sicuro di vedere a un certo istante la prima luce dopo il buio causato dal primo scudo." Spieghiamoci meglio…

Cominciamo col mettere gli scudi troppo vicini tra loro (s molto piccolo). Quello che succede è raffigurato in Fig. 15.

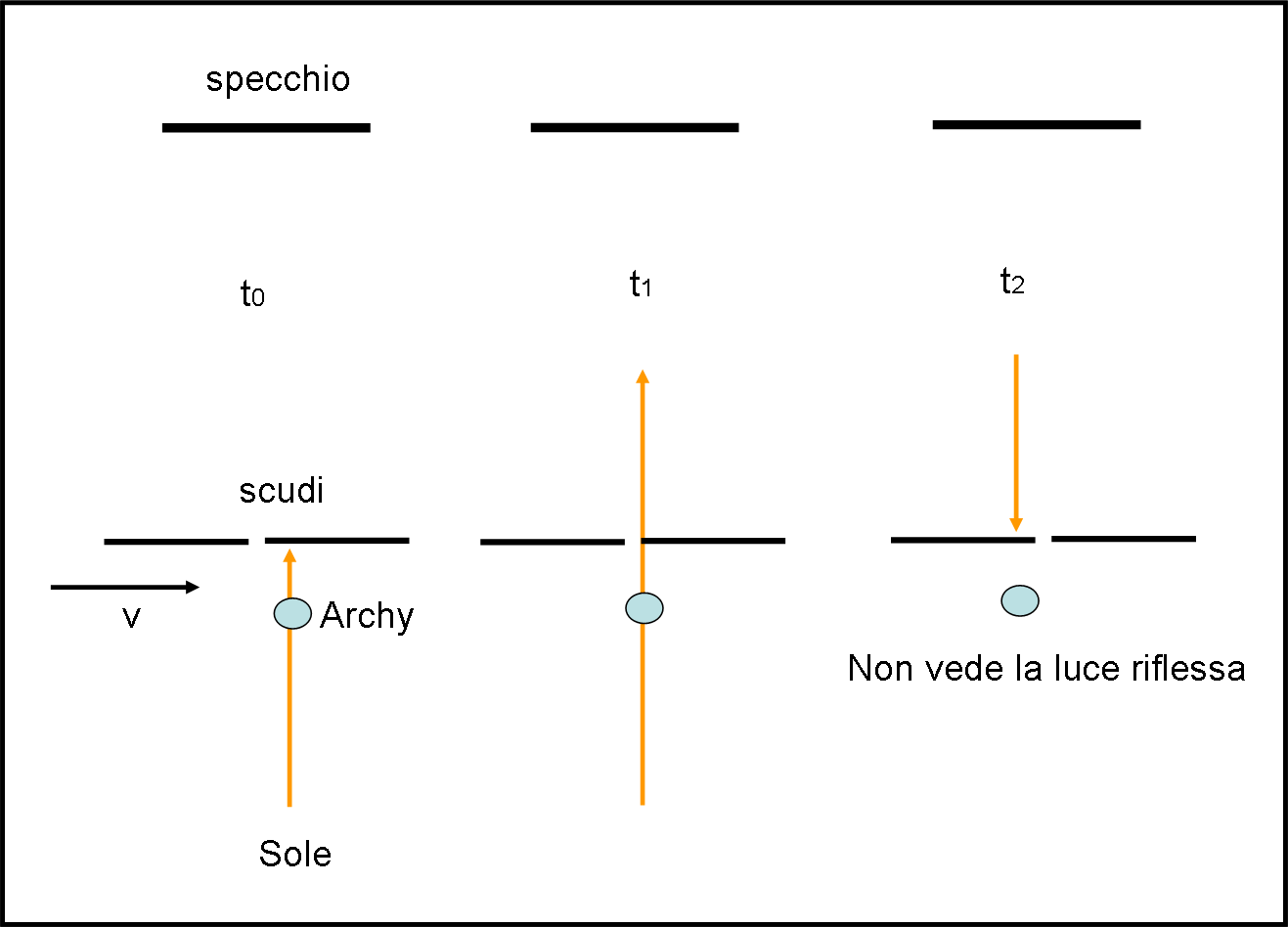
Al tempo t₀ il primo scudo blocca la luce del Sole e Archy non vede niente. Al tempo t₁ la luce riesce finalmente a passare nello spazio tra i due scudi. Quello è il raggio che Archy deve vedere tornare dopo essersi riflesso sullo specchio. Ma, la luce, per veloce che vada, impiega un certo tempo per tornare indietro. Lo spazio s è troppo piccolo e quando questo raggio ritorna, al tempo  t_2, all’altezza degli scudi non trova più lo spazio libero, ma il secondo scudo. Niente da fare, Archy non riesce a vedere la luce che torna indietro: per lui è sempre buio.

Facciamo, adesso, l’errore contrario, ossia lasciamo uno spazio troppo grande tra uno scudo e l’altro. Vediamo il risultato in Fig. 16.

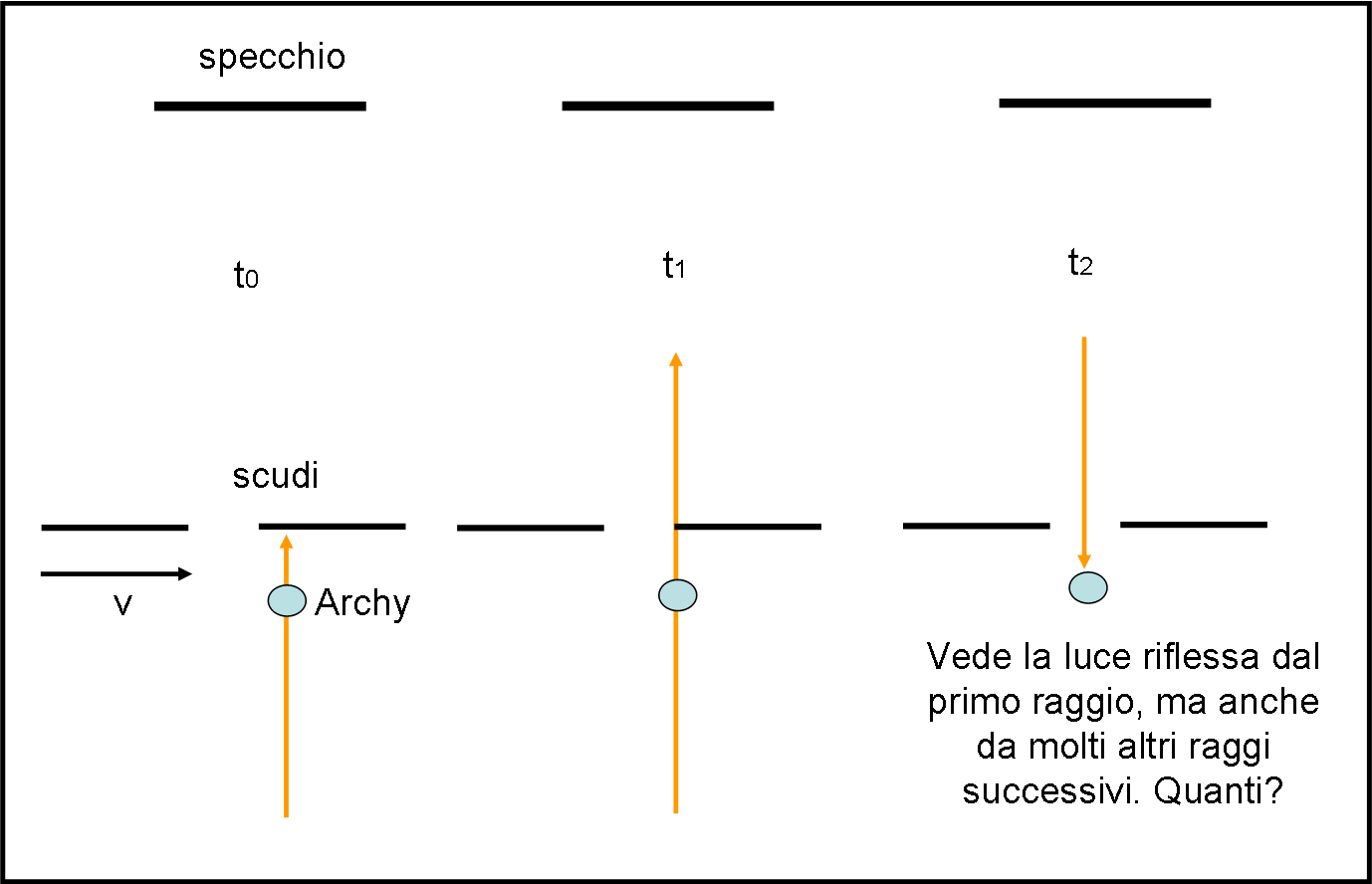
Al tempo t₀ il primo scudo blocca la luce, come nel caso precedente. All’istante t₁ il primo raggio riesce a passare. Quando torna indietro raggiunge lo spazio tra gli scudi al tempo t₂. Magnifico! No, non molto… anche negli istanti successivi Archy vede la luce riflessa e quindi è come se vedesse il secondo, il terzo, il quarto raggio e via dicendo. Non può certo sapere quante volte è successo e quindi non può concludere niente.

Pegaso e i suoi amici sono molto servizievoli (se ben pagati) e sono disposti a ripetere l’operazione un gran numero di volte. Ogni tentativo vede lo spazio diminuire sempre di più, in modo da passare dal secondo caso al primo. Stando molto attento, Archy nota un caso estremamente particolare: vede la luce solo per un istante brevissimo. Se lo spazio è solo leggermente più piccolo non vede più niente, se è solo un po’ più grande (e continua a crescere) nota che la luce riflessa rimane visibile sempre più a lungo. Lo spazio giusto da imporre ai due scudi è proprio quella che ha causato il lampo di luce più breve, subito dopo aver visto sempre buio. Le condizioni ideali sono quelle di Fig. 17.

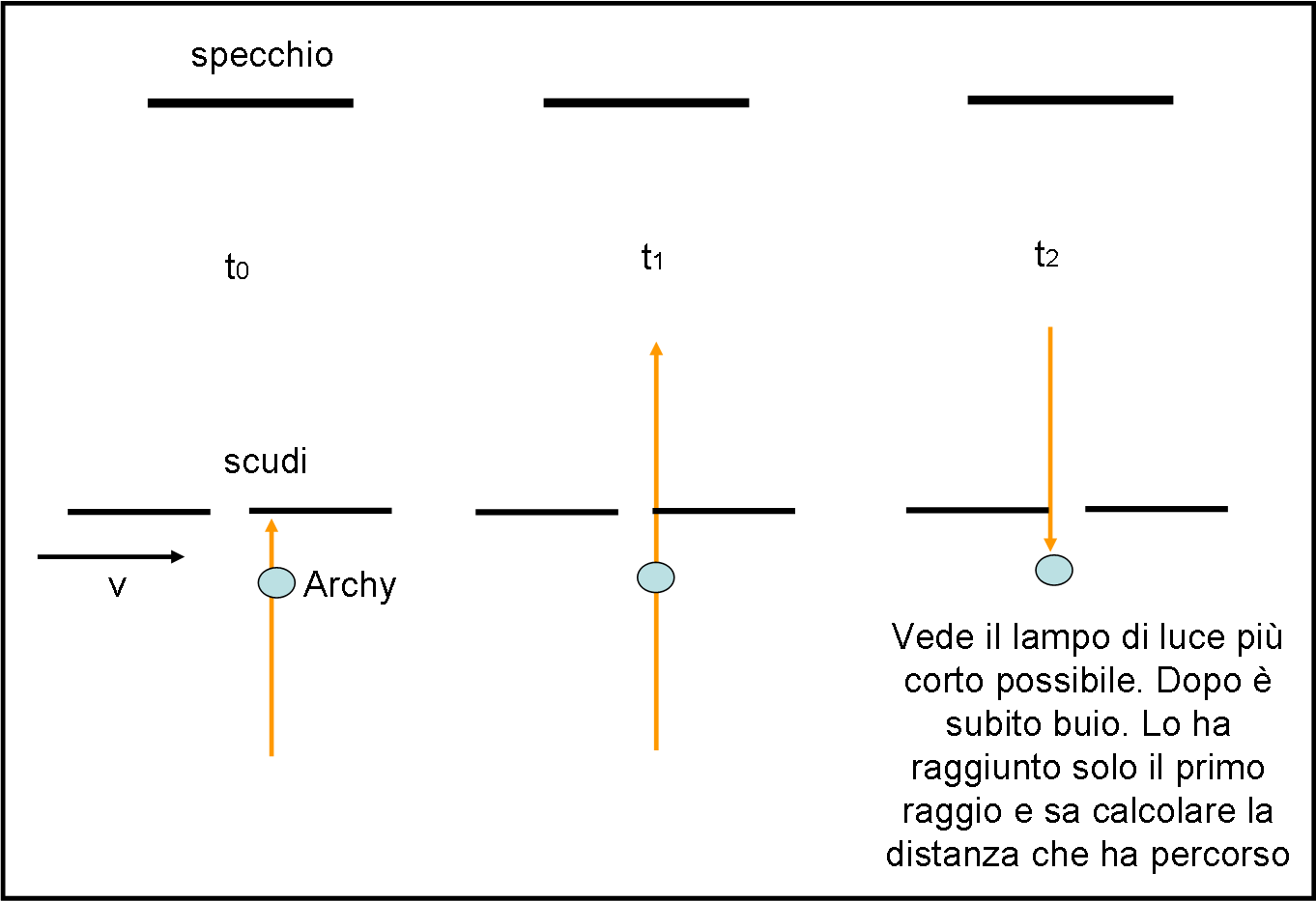
In t₀ succede sempre lo stesso. In t₁ il primo raggio passa dallo spazio vuoto. In t₂ il raggio riesce a passare “al pelo”, dato che quello successivo viene già bloccato dal secondo scudo. Eureka! Adesso sì che ci siamo. Abbiamo tutti i dati necessari per risolvere il problema.

Nello stesso intervallo di tempo che un raggio di luce impiega a passare nello spazio tra i due scudi e a tornare indietro fino ad Archy, Pegaso e i suoi amici si muovono di una lunghezza che è pari allo spazio tra i due scudi! Basta allora scrivere questo tempo in due modi, uno in relazione al percorso scudo-specchio-scudo, compiuto dalla luce, e l’altro in relazione allo spostamento degli scudi in funzione della velocità di Pegaso.

La prima relazione l’abbiamo già scritta:

t_R – t_A =  t₂ – t₁ = 2d/c                …. (1)

d è noto, mentre c è la grandezza da determinare.

La seconda è altrettanto semplice:

t₂ – t₁ = s/v                                 …. (2)

Ma v è la velocità costante di Pegaso, che è stata misurata su spazi e tempi ben più lunghi e vale 540 km/h. s non è altro che la distanza tra gli scudi che dà luogo al lampo più breve. Archy lo ha misurato e ha trovato s = 1 cm = 0.01 m = 0.00001 km. Trasformiamo la velocità di Pegaso in km/s. Si ha:

v = 540/3600 = 0.15 km/s

Basta allora uguagliare la (1) e la (2) (eliminando il tempo) e ricavare c:

2d/c = s/v

c = 2d v/s

c = 20·0.15/0.00001 = 300 000 km/s

Niente male! E bravo Archy, ma bravi anche Pegaso & co, senza dimenticare i due soldati e colui che ha lavorato gli scudi.

Da qui a Fizeau il passo è breve…

Va bene... abbiamo giocato un pochino, ma adesso torniamo a fare le cose seriamente.

Tutto sulla Terra

Prima di descrivere l’esperimento torniamo sul punto fondamentale, che Michelson ha risolto con l’interferometria e che Fizeau, nel 1849, aveva già risolto, come vedremo tra poco, in modo meno raffinato, ma altrettanto geniale. Per calcolare una velocità è necessario conoscere lo spazio percorso e il tempo impiegato a percorrerlo. Su questo dato di fatto c’è poco da fare. Nessun problema per uno spazio a misura d’uomo e la sua misura, ma molti e apparentemente invalicabili quelli riguardanti il tempo.

Utilizzando oggetti molto lontani, come i satelliti di Giove, il tempo diventa una grandezza alla portata di tutti, pur rimanendo molto impreciso. Al limite l’errore più grande proviene dalla conoscenza della distanza dei satelliti di Io ...

Se, invece, si vuole restare sulla Terra ed eseguire tutto in laboratorio o poco più, il “muro” del tempo ci riporta a quanto tentato inutilmente da Galileo. Michelson ha utilizzato una misura indiretta, ossia lo sfasamento dell’onda luminosa in funzione della differenza, anche piccolissima, del cammino ottico. Fizeau ha fatto qualcosa di molto più semplice, ma comunque geniale. Lo scopo finale è, come fatto dal nostro Archy, quello di eliminare l’intervallo di tempo impiegato, ossia trovare un altro fenomeno, che si svolga nello stesso infinitesimo tempo impiegato dalla luce tra andata e ritorno, i cui effetti siano ben visibili e calcolabili.

La ruota dentata di Fizeau

In parole molto povere se non possiamo risolvere la semplice equazione:

c = s/t

basta trovare un’altra velocità tale che

v = d/t

L’importante è che v, s e d siano noti e che t sia lo stesso. Si otterrebbe subito:

t = s/c

t = d/v

s/c = d/v

e infine:

c = s v/d

Come abbiamo visto, Archy aveva usato 4 cavalli alati e due scudi, Fizeau si è limitato a una ruota dentata, estremamente più facile da rifinire perfettamente e far girare a una velocità abbastanza ben determinata.

Raccontiamo il suo esperimento, utilizzando lo schema di Fig. 18.

la luce solare (o meglio di una potente lampadina S) viene inviata su uno specchio S₁ semitrasparente, inclinato di 45°, che la dirige parzialmente verso uno specchio S₂ posto a una distanza d. La luce torna indietro fino ad arrivare all’occhio O di Fizeau attraversando lo specchio S₁. Per “maneggiare” al meglio i raggi luminosi vengono usate varie lenti, che possiamo permetterci di trascurare, ma che si possono vedere nello schema originale di Fig. 19.

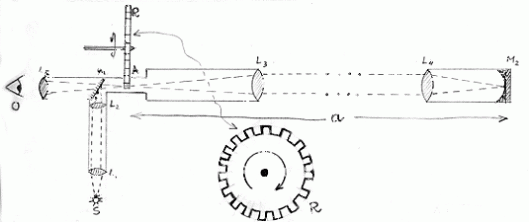
La cosa veramente importante è inserire una ruota dentata rotante R, attraverso i cui denti la luce è costretta a passare sia all’andata che al ritorno. La velocità della luce è data da:

 c = 2d/t

2d è conosciuto, ma non lo è t, il tempo impiegato dalla luce a percorrere il tratto ruota-specchio-ruota ed è impossibile misurarlo direttamente.

La luce inviata verso lo specchio, così come quella di ritorno, viene bloccata o lasciata passare a seconda che si trovi di fronte un dente vuoto o pieno della ruota. All’inizio, a ruota ferma, la  si sistema in modo che la luce proveniente da S passi da un vuoto. In tali condizioni O vede la luce al massimo della sua intensità, dopo che ha rimbalzato sullo specchio S₂. Poi viene messa in moto. Per velocità angolari ancora basse, la luce riesce ad andare e tornare attraversando lo stesso dente vuoto della ruota. Aumentando la velocità, la luce comincia a diminuire d’intensità, in quanto, al suo ritorno, comincia ad inserirsi il dente pieno. Per una certa velocità, la luce sparisce del tutto, in quanto il dente pieno ha presso esattamente il posto di quello vuoto. Se la ruota girasse ancora più velocemente, si tornerebbe a vedere un po’ di luce fino a che si avrebbe di nuovo un dente “vuoto” e la luce sarebbe nuovamente al massimo della sua luminosità.

Cosa è successo?

La ruota ha n denti pieni, ossia 2n intervalli tra il centro di un dente pieno e il centro di un dente vuoto. Sia ω la velocità angolare della ruota.

Sappiamo che:

ω = 2π/P

dove P è il periodo di rotazione della ruota. In altre parole, uno stesso dente si ritrova esattamente nella posizione originale dopo P secondi. Risulta, quindi, che il tempo necessario per passare da un dente vuoto a uno pieno è uguale a P/2n.

Quando appare il buio completo all’osservatore vuol dire che il tempo P/2n è esattamente uguale al tempo che la luce ha impiegato dal primo passaggio attraverso la ruota al suo ritorno. Il tempo impiegato dalla ruota è facile da calcolare, conoscendo la sua velocità di rotazione. Più facilmente si conoscono i giri al secondo compiuti dalla ruota, ossia la sua frequenza f = 1/P.

Il tempo t, ricavato dalla ruota, è:

t = P/2n = 1/2fn

La formula che dà la velocità della luce diventa, di conseguenza:

c = 2d/t = 4dfn

Fizeau aveva utilizzato:

d = 8.633 km

f = 12.6 giri al secondo

n = 720

da cui:

c = 4 · 8.633 · 12.6 · 720 ≈ 313.000 km/s

Il valore risutò piuttosto alto, dipendendo fortemente dalla misura di f. Nel 1850 Foucalt migliorò la strumentazione e dedusse un valore quasi perfetto (che descriveremo la prossima volta).

E' importante osservare che la velocità della luce così misurata è una media su un tragitto percorso due volte. La cosa era importante ai tempi di Fizeau, dato che si pensava ancora all’etere. Tuttavia, dato che il percorso era di andata e ritorno si poteva supporre che gli effetti della composizione della velocità della luce con quella del vento dell’etere si compensassero. Oggi, ossia dopo Michelson e Morley, sappiamo che la faccenda non aveva alcuna rilevanza.

Uno specchio rotante

Da Fizeau a oggi i maggiori passi in avanti sono stati soprattutto di tipo tecnologico. Noi ci limitiamo a descrivere le più importanti variazioni sul tema, che ci portano fino ad oggi.

L’esperimento di Fizeau aveva molti punti critici di tipo soprattutto tecnologico, ma era geniale nella sua impostazione di base. Era soprattutto la ruota dentata a dare i maggiori problemi. Ne seguì che gli sforzi posteriori si basarono soprattutto sulla sostituzione della ruota dentata con una strumentazione ottica più accurata. Ancora oggi è l’esperimento più usato per la determinazione della velocità della luce, utilizzando ovviamente quanto di più sofisticato ci sia in commercio.

Vale, quindi, la pena descrivere brevemente quanto fatto da Foucault l’anno dopo (1850), probabilmente in stretta collaborazione con lo stesso Fizeau. In particolare, il nuovo esperimento fu eseguito completamente in laboratorio, senza bisogno di avere grandi distanze a disposizione. Al posto della ruota dentata si inserì uno specchio rotante, capace di deflettere la luce di un angolo misurabile.

Innanzitutto, descriviamo uno dei punti fondamentali dell’apparato: il legame tra angolo di deflessione e angolo di rotazione dello specchio. Consideriamo la Fig. 20

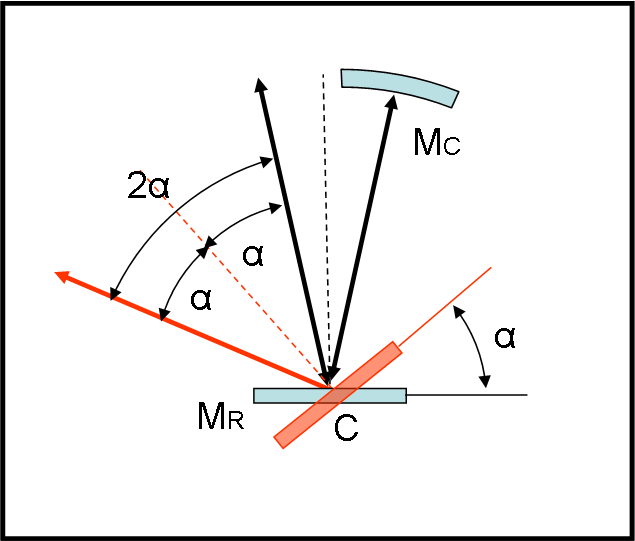
Per comodità sistemiamo lo specchio rotante M_R in posizione orizzontale. La luce proviene da S e viene riflessa mantenendo l’angolo di incidenza e va a colpire uno specchio M_C curvo, tale che il suo centro di curvatura sia proprio il punto C attorno a cui può ruotare M_R. Questa scelta comporta che tutti i raggi luminosi che vanno da C a un punto qualsiasi di M_C devono tornare indietro verso C per la stesso percorso.

Il raggio ritorna, quindi, in C. Lo specchio M_R non si è mosso e tutto è perfettamente uguale a ciò che è successo all’andata. Ragione per cui, il raggio di ritorno si riflette su M_R e torna verso S. Tutto questo percorso (di andata e ritorno) è segnato con le linee nere.

Il passo successivo ha l’inizio tale e quale: la luce parte da S, colpisce M_R in C e  si riflette raggiungendo M_C. Poi torna indietro per la stessa strada. Nel frattempo, però, lo specchio M_R è stato ruotato di un angolo α. Il raggio che proviene da M_C colpisce M_R in C, ma la riflessione deve avvenire simmetricamente rispetto all’asse dello specchio che è ora la linea tratteggiata rossa. Il raggio, perciò, torna indietro seguendo la linea rossa continua. Da considerazioni geometriche immediate, segue che l’angolo tra raggio di andata (nero) e raggio di ritorno (rosso) è esattamente uguale a 2α. Questa conclusione è di grande importanza dato che lo spostamento tra la sorgente e l’immagine finale è strettamente legata all’angolo 2α.

Guardiamo, allora, lo schema dell’intero apparato in Fig. 21.

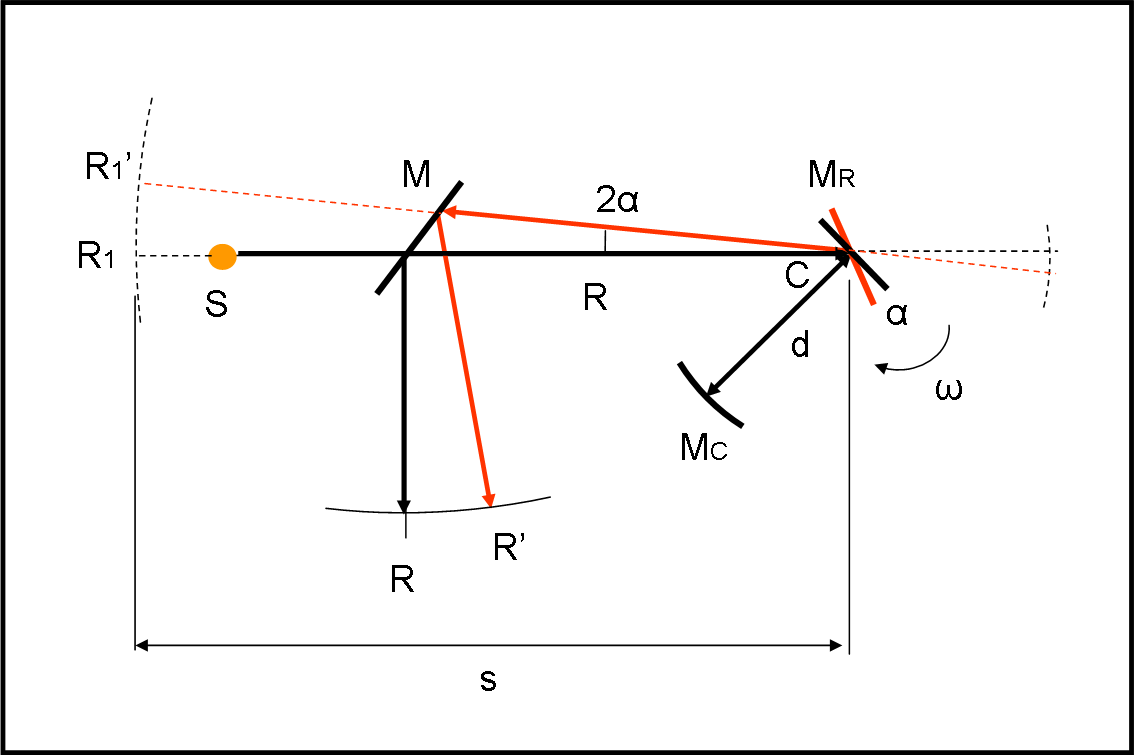
La sorgente S invia la luce che attraversa uno specchio M semiriflettente, in modo che una parte prosegua verso lo specchio rotante. L’andata è rappresentata dalla linea nera. Se lo specchio rotante è fermo, la luce torna indietro per lo stesso percorso e lo specchio M la invia verso la superficie di raccolta finemente graduata. Si ottiene la posizione R. Ripetiamo l’osservazione, ruotando però lo specchio M_R durante il “viaggio” M_R-M_C e ritorno. Lo specchio M_R è ruotato di α, mentre il raggio rosso che torna indietro è adesso ruotato di 2α rispetto a quello precedente. Esso va a colpire la superficie di raccolta in R’.

Sappiamo quanto vale la velocità angolare della rotazione dello specchio M_R:

ω = 2π/P

P è, ovviamente, il periodo di rotazione.

Ma vale anche:

ω = α/t

t = α/ω          …. (1)

Andiamo, adesso, a studiare da vicino cosa succede tra M_R e M_C. In un certo tempo t la luce deve andare da M_R e tornare dopo la riflessione. Si ha perciò che la velocità della luce  è data da:

c = 2d/t         …. (2)

Nello stesso tempo, però, sappiamo di quanto è ruotato lo specchio attraverso la (1). Sostituendola nella (2) si ha:

c = 2dω/α

d è noto e ω può essere cambiato dall’operatore. Ovviamente, essendo il tempo sempre lo stesso (dipende solo dalla distanza d e dalla velocità della luce) la (1) ci dice che per avere un angolo α misurabile deve anche essere molto elevata la ω.

Ma come facciamo a misurare l’angolo α? Niente di più facile! Guardando di quanto si sposta la posizione di R’ rispetto a R. Infatti, R e R’ possono essere ribaltati in R₁ e R₁’. Facendo centro in C si ottiene l’arco di cerchio R₁R₁’. Misurare RR’ è come misurare R₁R₁’ e conoscendo la distanza s si misura facilmente l’angolo 2α.

Questo fatto comporterebbe una deformazione circolare della superficie di osservazione. In realtà, l’angolo è molto piccolo e si può tranquillamente approssimare l’angolo con la sua tangente e quindi usare una superficie piana.

La strumentazione era decisamente più complicata, dovendo tener conto di lenti aggiuntive che dovevano focalizzare i fasci di luce. Il concetto, però, è quello illustrato precedentemente in modo semplificato.

Foucault ottenne un valore di c pari a 298 000 km/s, decisamente migliore di quella di Fizeau. Ricordiamo che quello  accettato oggi è pari a 299 792 km/s

Dopo Foucault, molti altri utilizzarono il suo metodo, cercando di migliorare le condizioni di misura e la strumentazione. Uno di questi fu proprio Michelson che provò svariate volte, sostituendo anche lo specchio rotante con uno specchio ottagonale e aumentando enormemente la distanza tra specchio rotante e specchio fisso (35 km): il primo sul Monte Wilson e il secondo sul monte Backly (Fig. 22). Egli ottenne il valore di  (299 796 +/- 4) km/s.

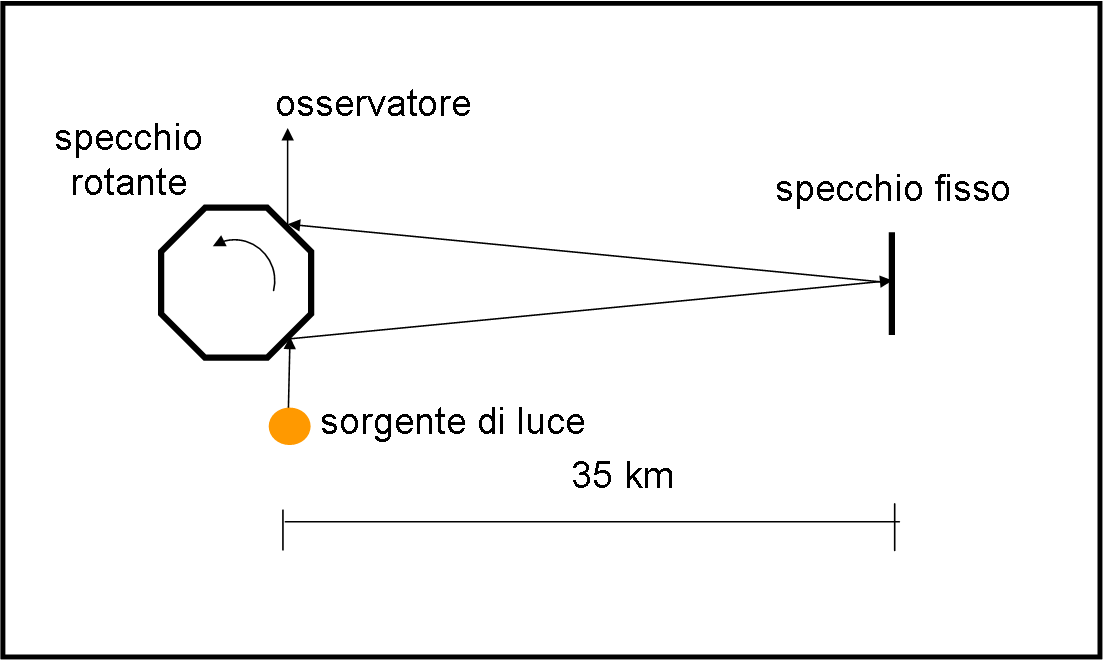
Lo schema è molto semplice e la velocità di rotazione è quella in grado di ottenere la situazione simmetrica della figura. Lascio a voi i facili calcoli necessari…

E’ interessante comprendere quanta accuratezza veniva messa nelle misurazioni e nelle apparecchiature. A titolo di esempio, riportiamo un articolo scritto dallo stesso Michelson mentre lavorava al Naval Observatory di Washington (circondato da un magnifico parco che pullula di simpaticissimi procioni lavoratori… non me ne sarei più andato…).

 

Volete vedere Gatto Gualtiero (con le sue fusa) che si "propaga" su Alan, mentre ci racconta il fallimento più importante della storia della Fisica? Eccolo QUI!

Se siete abbastanza curiosi, QUI troverete alcuni "strani" metodi casalinghi (o quasi) per misurare la velocità della luce!

E se la velocità della luce fosse diversa da quella che è? Ne abbiamo parlato QUI...