Categorie: Fisica classica
Tags: forza di Coriolis forze fittizie moto circolare quiz sistemi NON inerziali traiettorie velocità angolare
Scritto da: Vincenzo Zappalà
Commenti:28
Quiz geometrico sui sistemi non inerziali: tagliamo la corda! **
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
Dopo esserci esercitati con i sistemi inerziali, proviamo a fare un passo in avanti e introduciamo un sistema rotante. Il gioco si complica un poco, ma ritroveremo una cara amica conosciuta da poco…
Finora ci siamo divertiti con palline che cadono dal treno o pezzi di ferro lanciati verso l’alto. Abbiamo visto che ciò che comanda il tutto è solo e soltanto il principio d’inerzia. Tutto ciò che corre o sta sul treno si muove a velocità costante e quindi mai nessuno potrebbe dire se si muove o se sta fermo. Inoltre, ciò che capita stando fermi deve capitare perfettamente anche in un sistema che si muova a velocità costante. Sono cose che già sapevano bene sia giordano Bruno (prima) che Galileo (dopo).
Si potrebbe, adesso, fare muovere il treno con velocità crescente o fare scappare il bimbo a velocità maggiore. I sistemi (quello “fermo” e quello in movimento) non vedrebbero più la stessa cosa, dato che non sono più inerziali. Tuttavia, sono concetti che già abbiamo trattato e, quindi, facciamo un passo un po’ più lungo ed entriamo nei sistemi in rotazione. Proprio per essere buoni, facciamo, però, ruotare il sistema con velocità angolare costante.
La matematica ci è già venuta in aiuto, permettendoci la trasformazione della posizione, velocità e accelerazione (QUI). Tuttavia, basta con la matematica e limitiamoci alla geometria. Le cose da scoprire sono, comunque, tante e magari anche inaspettate.
Facciamo, allora, tornare in campo i nostri cari amici Pippo e Pappo (ricordate?), ormai diventati “grandi”, ma sempre volenterosi di scoprire il mondo della fisica. Non fanno più scommesse per guadagnarsi un pezzo di torta in più, ma discutono spesso sui fenomeni della Natura e si pongono l’un l’altro tante domande, stimolando vari esperimenti di facile costruzione.
Entriamo, perciò, nel loro giardino e ascoltiamo il discorso che sembra molto interessante. Al centro vediamo una piattaforma circolare (probabilmente una vecchia giostra di quando erano bambini) che può ruotare a velocità costante. Su di lei, proprio lungo il bordo esterno, vediamo Pippo, con una pallina in mano, seduto su un seggiolino. Pappo, invece, è situato al di fuori della “giostra”.
Stanno parlando di forze centripete e centrifughe e sono piuttosto accalorati. Innanzitutto, capiamo benissimo che stanno escludendo del tutto la forza di gravità terrestre, ossia cercano di costruire un esperimento come se fossero liberi nello spazio, lontano da qualsiasi massa ingombrante. Va bene, lo facciamo anche noi…
Il succo di tutto è esprimibile con una domanda ben chiara: “Che traiettoria segue la pallina se viene lasciata libera da Pippo mentre sta girando con la giostra?” Non vogliono fare calcoli più o meno difficili, ma solo risolvere il problema con la geometria. Prima di far girare la giostra e vedere la soluzione, vogliono prevedere il risultato. Non sono sprovveduti e quindi sanno già cosa aspettarsi e, soprattutto, sanno che ciò che vede Pappo è ben diverso da quello che vede Pappo. Il fenomeno meccanico deve essere lo stesso, ma la sua descrizione completamente diversa, dato che i loro sistemi di riferimento non sono inerziali.
Abbiamo capito ciò che vogliono fare e possiamo tornare nel nostro studio e, con carta, matita e compasso (e magari un goniometro, ma non ce ne sarebbe nemmeno bisogno…), imitare i nostri amici e magari fare più in fretta di loro. Usiamo solo la nostra testa e le nostre mani o –ce lo possiamo permettere- il PC come matita, compasso e goniometro, ma evitiamo di cercare programmi già preparati allo scopo (almeno in una prima fase).
Semplifichiamo il problema da risolvere, considerando due sistemi di riferimento, aventi la stessa origine, e manteniamo tesa un corda fissata all’origine, che porta all’altra estremità una palla di ferro. In altre parole, simuliamo un lanciatore di martello. Chi è fuori dalla pedana, nello stadio, vede ruotare la palla, tenuta a distanza costante dal centro, attraverso la corda che deve rimanere ben tesa. La sfera, invece, si sente sempre ferma nel suo sistema rotante. Possiamo dire tranquillamente (un piccolo aiuto che è alla portata di tutti) che per chi è nello stadio esiste solo una forza centripeta (la corda) che evita che la palla scappi verso il pubblico. E’ lei che costringe la palla a ruotare invece di mantenere il suo moto rettilineo uniforme. La palla, invece, si sente ferma e SENTE, anche molto bene, una forza che la porterebbe verso l’esterno, in direzione opposta a quella del centro. Se non ci fosse la corda che la tiene ferma seguirebbe questa forza estremamente violenta (dipende molto dalla rotazione impartita). In parole semplici. Lo spettatore dello stadio vede la palla ruotare, mentre la palla vede corda e se stessa sempre ferme.
Le domande che ci facciamo sono quindi le stesse di Pippo e Pappo: invece di lasciare libera la pallina... tagliamo la corda! No, no, non andarcene via, ma tagliare veramente la corda che tiene unita la palla con l’origine degli assi. A questo punto ci chiediamo:
1. Che traiettoria segue la palla se il fenomeno è visto dal sistema “stadio”, ossia dal sistema che possiamo considerare fermo?
2. Che traiettoria segue la palla se il fenomeno è visto dal sistema rotante (che continua a ruotare anche se la corda viene tagliata)?
Senza troppi fronzoli, la situazione è quella rappresentata in Fig. 1.
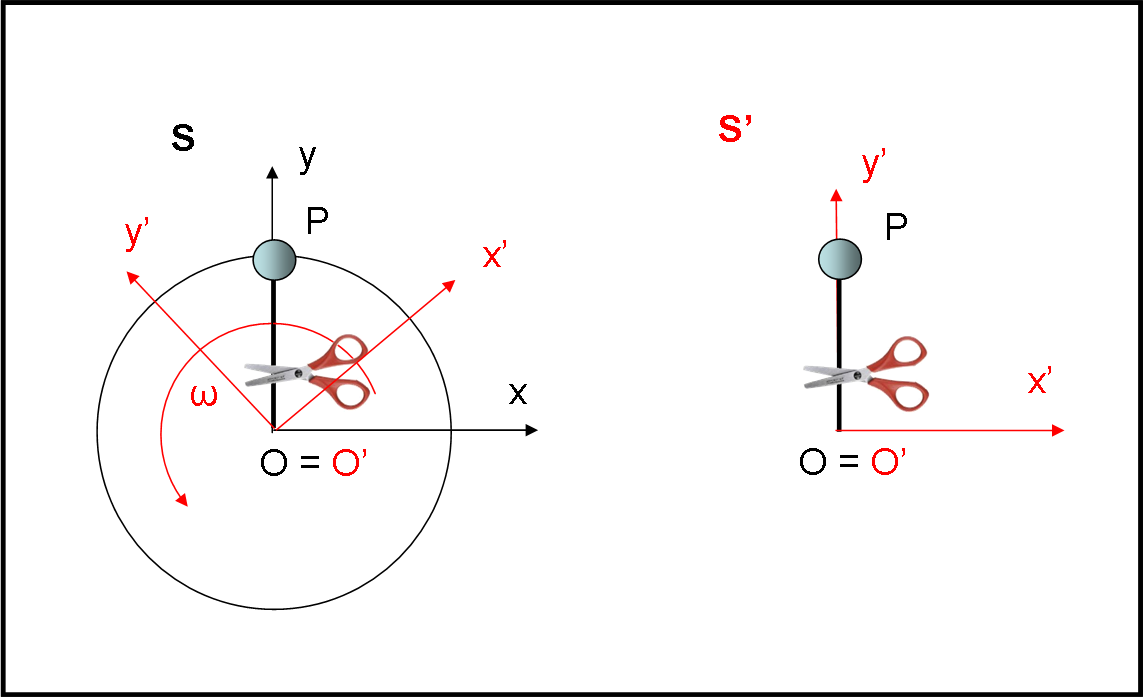
Abbiamo due sistemi di riferimento: uno nero (fermo) e uno rosso (rotante con velocità angolare ω). La palla P è solidale, ovviamente, con il sistema rotante. Uno ha assi x, y e z, l’altro x’, y’ e z’. Tuttavia, l’asse z coincide con z’, dato che rappresenta l’asse di rotazione. Possiamo immaginarlo diretto verso di noi, perpendicolare al foglio e quindi evitare di disegnarlo. Limitiamoci al piano x,y che coincide con il piano x’,y’ (il piano, non gli assi!). Per rispondere alla prima domanda dobbiamo riferire il moto agli assi immobili x e y. Per rispondere alla seconda domanda dobbiamo riferire il moto agli assi x’ e y’ immaginati fermi.
Per rendere più quantitativo il nostro problemino, diamo dei valori numerici. Il minimo indispensabile!
Raggio OP = O’P = 4 metri
Periodo di rotazione del sistema (e quindi anche della palla prima del taglio della corda) = 16 secondi (notate che la scelta non è casuale, ma permette di disegnare al meglio momenti diversi della rotazione.
La descrizione del fenomeno deve essere fatta per punti e poi cercare di unirli nel modo migliore, sempre che ve ne sia bisogno…
Ricordiamo ancora: abbiamo escluso la forza di gravità che tenderebbe a far cadere al suolo la palla in tempi piuttosto brevi.
Un’ultima richiesta: tracciamo il percorso della palla almeno per metà del periodo di rotazione!
Evitiamo, comunque, tentativi analitici di soluzione… vogliamo che tutti possano ottenere il risultato con mezzi elementari.
QUI la soluzione
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis






28 commenti
Anche senza compasso e goniometro (che a me piace molto ma non sempre mi lasciano usare) si può fare questa osservazione:
Il peso si allontana dal centro del cerchio lungo una traiettoria rettilinea, secondo la direzione tangenziale alla circonferenza nel momento in cui è stata tagliata la corda, e si muove con moto uniforme. Nel frattempo il sistema di riferimento rotante(rosso) continua a girare con velocità angolare costante.
Dopo un giro completo, il sistema rotante si ritrova con gli assi orientati esattamente come all'inizio. In questa situazione vedrà che la palla P si è allontanata lungo l'asse x ( della distanza coperta nel periodo di rotazione di 16 secondi, alla velocità che si può facilmente calcolare, che aveva al momento del taglio della corda) mentre la distanza lungo l'asse y è la medesima misurata in quello stesso momento , uguale al raggio.
Questa situazione si ripete ad ogni ciclo...
Non dico altro su cosa succede nelle altre posizioni del sistema rotante se no il prof. mi licenzia.
Abbiamo due sistemi di riferimento, uno in moto rotatorio rispetto all’altro e che condividono la stessa origine O = O’.
Assumendo come verso di rotazione del sistema X’O’Y’ quello antiorario, con i dati:
R = 4 m.
P = 16 sec.
Si avrà una frequenza di rotazione pari a:
f = 1 / P = 1 / 16 = 0,0625 giri/sec
velocità angolare della palla e della corda:
ω = 2πf = 2 * 3,1415 * 0,0625 ≈ 0,3927 sec^-1 π / 8 sec^-1
velocità angolare misurata in gradi:
ω° = 360° * f = 360° * 0,0625 = 22°,5 sec^-1
ovvero il raggio spazza 22°,5 al secondo
velocità tangenziale della palla:
v = ωR = 0,3927 * 4 ≈ 1,571 m/sec π / 2 m/sec
Per semplicità, si può ipotizzare di tagliare la corda quando il sistema X’O’Y’ è perfettamente sovrapposto con il sistema XOY (angolo di rotazione 0°).
Nell’istante del taglio della corda,
1. Che traiettoria segue la palla se il fenomeno è visto dal sistema “stadio”, ossia dal sistema che possiamo considerare fermo?
lo spettatore del sistema di riferimento stadio (quello “fisso”) XOY, dovrebbe vedere la palla viaggiare in linea retta (si usa dire: è partita per la tangente), con direzione perpendicolare a quella della corda (direzione X’=X), con direzione parallela all'asse Y, verso quello dell’asse positivo Y e con velocità costante (moto rettilineo uniforme);
2. Che traiettoria segue la palla se il fenomeno è visto dal sistema rotante (che continua a ruotare anche se la corda viene tagliata)?
l’ipotetico osservatore posto a “cavallo” della corda e solidale con essa, sistema di riferimento rotante X’O’Y’, vedrebbe la palla disegnare sul piano di rotazione una traiettoria curvilinea verso destra (verso positivo asse X).
La distanza percorsa dalla palla, nel sistema di riferimento XOY (quello fisso, lo stesso dello stadio) sarà:
Sy = v * t = (π/2) * t (metri)
Tempo t in secondi distanza percorsa in metri
1 π/2 ≈ 1,571
2 2*π/2 ≈ 3,142
3 3*π/2 ≈ 4,712
4 4*π/2 ≈ 6.283
5 5*π/2 ≈ 7.854
6 6*π/2 ≈ 9,425
7 7*π/2 ≈ 10,996
8 8*π/2 ≈ 12.566
9 9*π/2 ≈ 14.137
10 10*π/2 ≈ 15,708
11 11*π/2 ≈ 17,279
12 12*π/2 ≈ 18,850
13 13*π/2 ≈ 20,420
14 14*π/2 ≈ 21,991
15 15*π/2 ≈ 23,562
16 16*π/2 ≈ 25,133
Come sempre, chiedo anticipatamente venia al prof. Zappalà per eventuali baggianate scritte
cari amici miei... tutto molto interessante, ma io chiedevo anche di disegnare la traiettoria per punti...
" La descrizione del fenomeno deve essere fatta per punti e poi cercare di unirli nel modo migliore, sempre che ve ne sia bisogno…"
Un disegno... voglio vedere un disegno
Chi non ha l'accesso diretto, come Andy, può anche inviarlo a Scherzy (ne sarà CONTENTISSIMO ) e lo pubblicherà lui... Vanno bene anche disegni a mano libera, ma che spieghino bene le operazioni fatte...
) e lo pubblicherà lui... Vanno bene anche disegni a mano libera, ma che spieghino bene le operazioni fatte...
Pippo e Pappo stanno lavorando e anche bene, da quanto vedo... Sbrigatevi!!!!!
Ok, ok... chi ha bisogno di pubblicare un'immagine (va bene anche una foto) e non sa come fare, la può inviare a papalscherzone@gmail.com
Scusa, Scherzy , ma la foto deve essere con l'espressione seria come per la carta di identità ? o va bene anche un'istantanea?
Va bene tutto... ma il burka no, per carità!
Allora, andiamo per gradini....
Fatto il disegno del sistema rotante e trasferite le coordinate con cui individua il punto in movimento ad ogni secondo ( solo per i primi 4 secondi). Verrebbe una cosa così...
Se non si capisce bene ( che, data la qualità del disegno sarebbe anche logico) chiedete pure, che qui a Cuneo siamo sempre disponibili.
la finite di fare i buffoni! I disegni, voglio i disegni.... non chiacchiere... alla fine crederanno che questo sia una specie di BLOB, non un BLOG scientifico (o quasi...)
Questo è un disegno, magari non sarà preciso, ma è un disegno, a differenza della pipa di Magritte.
In effetti... l'ultimo punto H è proprio sbagliato, perché in quel punto la coordinata y' è negativa e vale -R.
Quindi il disegno (giusto?) per il primo mezzo giro, che si compie in 8 secondi, è questo:
1. Che traiettoria segue la palla se il fenomeno è visto dal sistema “stadio”, ossia dal sistema che possiamo considerare fermo?
La palla segue una traiettoria rettilinea tangente alla circonferenza nel punto P.
2. Che traiettoria segue la palla se il fenomeno è visto dal sistema rotante (che continua a ruotare anche se la corda viene tagliata)?
In pratica si tratta di osservare la palla , che dall'istante t=0 di taglio della corda percorre una traiettoria rettilinea tangente alla circonferenza nel punto P, nel sistema di riferimento solidale alla giostra, cioè in rotazione con velocità angolare omega. Il quesito chiede di determinare la traiettoria della palla, non di dire cosa vede l'osservatore solidale alla giostra e che gira insieme ad essa. Infatti, se io mi trovassi in corrispondenza dell'asse di rotazione della giostra e girassi attorno ad esso insieme ad essa, a parte il fatto che dopo un po' comincerebbe a girarmi la testa e cadrei per terra, vedrei la palla finché rientra nel mio campo visivo. Ad un certo punto mi ritroverei con le spalle verso la palla che va per la tangente, quindi non potrei vederla. Poi, continuando io a ruotare, ad un certo punto la palla rientrerebbe nel mio campo visivo anche se mi apparirebbe più lontana avendo essa nel frattempo percorso una certa distanza e così via.
Tornando al quesito, abbiamo che la palla, al momento del taglio della corda ha velocità tangenziale v = omega * R che, per i dati del problema, vale pigreco/2 m/s. Essendo la velocità angolare della giostra pari a 2pigreco radianti in 16 secondi, ogni 2 secondi la giostra girerà di un angolo pari a pigreco/4 . Corrispondentemente, la palla si sposterà verso sinistra ogni 2 secondi di pigreco metri.
Ho, allora, disegnato la circonferenza, gli assi cartesiani e la posizione della palla (indicata con la lettera Q nel sistema fisso e con la lettera P in quello della giostra) ogni 2 secondi. Purtroppo, il disegno in bella è venuto troppo grande, per cui già per t=6 s il punto Q esce quasi fuori dal foglio. Ad ogni modo, per ciascun istante considerato ho anche disegnato il sistema cartesiano della giostra, centrato sempre in O e ruotato in senso antiorario di un angolo teta pari a quello spazzato da t=0 all'istante t considerato. Sono poi andato a misurare con il righello le coordinate del punto Q rispetto a tali assi cartesiani ruotati, ottenendo così le coordinate dei punti P , cioè delle posizioni della palla nel sistema della giostra. Infine, ho disegnato un nuovo sistema cartesiano di riferimento in cui ho disegnato (per i primo mezzo giro) la posizione dei punti P in base alle suddette coordinate ed ho ottenuto la traiettoria cercata. Essa somiglia ad un tratto di spirale.
la butto lì veloce. Nel sistema stadio è ovviamente una retta tangente.
Ma nel sistema "rotante" , per il principio di relatività (galileiana) ciò il rotante vede la palla come la palla vede il rotante. Ma se la palla sta su una retta tangente alla circonferenza la curva descritta dalla circonferenza si chiama cicloide, curva facile da disegnare.
Ho messo un disegno qui:
https://i.imgur.com/058pNw4.jpg
Vedremo
Proseguendo nella tracciatura della curva fino ad un giro completo (16 secondi), si ottiene questo grafico che fa proprio pensare che la curva sia una spirale, come già si intuiva dopo il primo mezzo giro ( Arturo lo ha anche scritto).
Ma dirò di più... se è vero che, data la velocità costante, ad ogni giro che si completa la x varia sempre della stessa quantità rispetto al giro precedente.... si tratta di una spirale di Archimede!
Bene, bene... bei disegni...
diciamo che c'interessa abbastanza poco il tipo di curva descritta (da un punto di vista matematico), ma il fatto stesso che sia una ... curva. Sappiamo bene che per avere una traiettoria curva, è necessario che sul corpo agisca una forza. Ma chi l'ha mai data alla nostra pallina? L'unica che aveva (centripeta) gliel'ha abbiamo tolta.
Per Arturo:
noi non vogliamo metterci sulla pallina che, ovviamente, si considererebbe ferma, ma vogliamo vedere il suo percorso se stessimo girando con il sistema rotante, ossia se fossimo solidali con l'asse x' o y' o quello che vuoi. Il fatto di girare la testa ha poca importanza. Potremmo anche alzarci in volo lungo l'asse z e guardare il tutto dall'alto, dato che continuiamo a ruotare con il sistema x',y',z'. Il sistema non è solo il piano, ma il percorso della pallina si svolge su un piano.
Non mi piace infatti che la pallina vada verso sinistra...
Si, Vincenzo, in effetti se il sistema solidale alla giostra ruota in senso antiorario, la pallina, rispetto all'osservatore solidale alla giostra (nel senso che hai detto, cioè come se fosse sollevato dalla giostra e la guardasse restandoci vincolato) va via in senso orario. Basta cambiare segno alle ascisse dei punti unendo i quali ho ottenuto la traiettoria.
Il sistema rotante non è un sistema inerziale e vede le cose a modo suo.
Quando la forza (centripeta) c'era non la vedeva, infatti credeva che la pallina fosse addirittura in quiete. Adesso che abbiamo tolto la forza (centripeta), interpreta la soppressione della forza come l'applicazione alla pallina di una forza (uguale e contraria a quella centripeta) , e vede la traiettoria della pallina curvarsi per l'azione di tale forza, mentre in realtà la curva è solo l'apparenza prodotta dalla sua stessa rotazione. Se la smettesse di ruotare diventerebbe un sistema inerziale e non vedrebbe più la curvatura a spirale. Ma i sistemi rotanti sono testardi e non c'è modo di convincerli.
Perfetto... ma qual è questa forza? la centrifuga? o che altro?
Dovrebbe essere "che altro", perché sembra agire in una direzione trasversale alla traiettoria...deviando la pallina.
magari leggendo l'articolo su Coriolis... si può capire (e costruire anche la velocità ...)
http://www.infinitoteatrodelcosmo.it/2017/11/11/gira-mondo-gira-la-forza-coriolis-1-determinazione-matematica/
Nel sistema di riferimento in rotazione, chi sta dentro vede che, dal momento del taglio della corda, la palla:
1) sembra trascinata lateralmente da un filo invisibile mentre avanza;
2) allo scorrere di pezzettini di tempo tutti uguali tra di loro, “appare” che la palla copra pezzi di spazio di ampiezza differente, il precedente dall’attuale, l’attuale dal successivo.
Cominciano a ricadere dei sospetti sul nostro amico Coriolis
Leggendo l'articolo fino in fondo si può sapere anche da quali componenti è costituita l'accelerazione, e dare il giusto nome alle corrispondenti forze... Tutto è scritto, nel grande libro dell'infinito Teatro, il perché e il percome.
A me viene una figura di questo tipo. Quella sopra è nel riferimento dello stadio e quella sotto nel riferimento rotante.
La palla mantiene il valore della sua velocità iniziale che al taglio è diventata rettilinea.
La distanza percorsa dalla palla dopo un giro completo del riferimento è pari a quella della circonferenza.
Nella figura P0 P16 = 6,28*4 sia nella figura sopra che in quella sotto.
Per questo le linee blu sono quelle che otterrei avvolgento un filo al circonferenza per poi srotolarlo mentenedolo teso.
Nel sistema rotante la palla si allontana dal centro quindi ci deve essere una accelerazione centrifuga.
Inoltre le distanze percorse in tempi uguali sembrano aumentare. Questo dovrebbe corrispondere ad una accelerazione nella direzione del suo moto.
Quantitativamente non riesco a derivarle dal grafico.
caro Fabrizio,
basta applicare le formule dei sistemi relativi... ci sono solo prodotti vettoriali, tra vettori sempre ortogonali... I moduli sono tutti noti...
Quindi la curva è l'evolvente della circonferenza... Interessante.
Le considerazioni che ho fatto sulle accelerazioni non sono totalmente corrette perchè fanno pensare che l'accelerazione che allontana la palla dal centro del riferimento sia diversa da quella che fa aumentare la velocità della palla. Ho fatto confusione tra radiale rispetto al riferimento e radiale rispetto al moto della palla.
Invece l'accelerazione radiale rispetto al riferimento può essere la stessa che produce l'accelerazione nella direzione del moto della palla. E' evidente subito dopo il taglio della corda quando il movimente della palla è prevalentemente radiale rispetto al riferimento. Qui si vede anche l'accelerazione perpendicolare al moto della palla che la fa deviare a destra.