In questo articolo vogliamo spiegare bene come agire per risolvere le  domande del quiz sull’astronave aliena, in modo da ottenere una piena comprensione delle rappresentazioni nei sistemi non inerziali (si fa sempre molta fatica...).  La spiegazione era già stata data nella risposta al quiz del taglio della corda, ma forse è meglio richiamarla sia per comprendere ancora meglio quanto trattato in quel quiz, sia per essere pronti ad andare verso costruzioni leggermente più difficili…

Il mistero degli alieni che sembrano avercela proprio con l’Italia è di una banalità spaventosa e, proprio per questo, temo che crei dei problemi del tutto inesistenti. A volte il troppo facile e il troppo difficile si toccano. Lo scopo, comunque, non è tanto risolvere il quiz, quanto prendere sempre più dimestichezza con le rappresentazioni in un sistema non inerziale.

Se in quello esterno, fisso, tutto torna molto bene (basta mettersi in un punto esterno e guardare cosa succede), è molto più complicato, mentalmente, immaginarsi fermo in un sistema rotante. E’ vero che lo proviamo tutti i giorni, sia in macchina che su una giostra, ma noi SAPPIAMO di stare ruotando e molte cose che capitano vengono travisate o confuse. Dobbiamo fare lo sforzo mentale di sentirci veramente FERMI, anche quando ci si muove!

La cosa migliore da fare, per rappresentare ciò che si vede in un sistema rotante, è bloccare le condizioni di partenza e riferire tutto ciò che si osserva a quelle condizioni. In tal modo l’osservatore si considera fermo qualsiasi cosa faccia il suo sistema di riferimento.

Prima, risolviamo il piccolo mistero con il solo ragionamento e poi lo descriveremo con un disegno riferito al sistema rotante. Utilizziamo lo schema di Fig. 1.

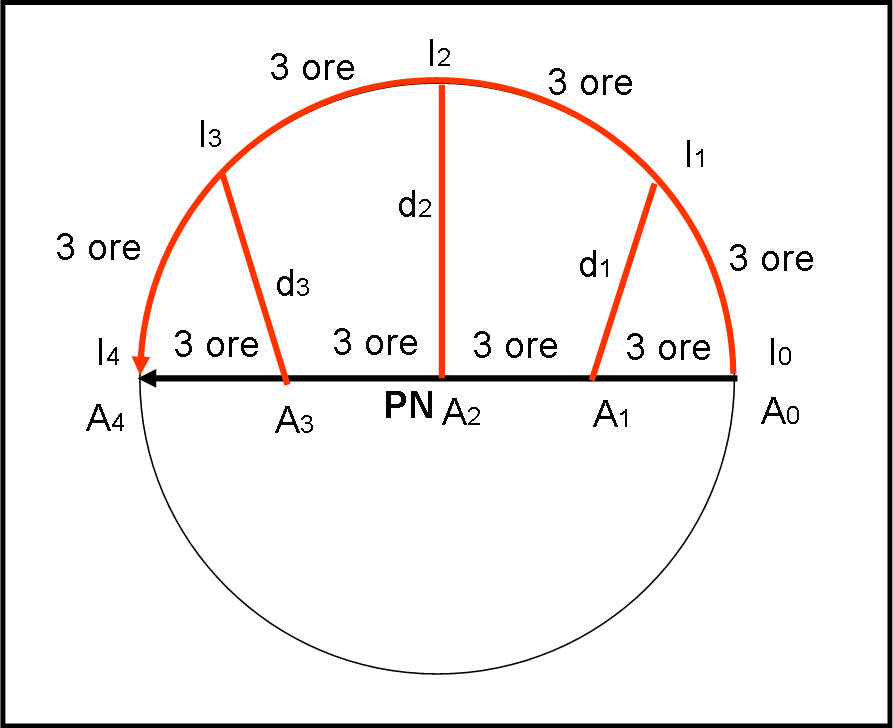
Continuiamo a proiettare tutto nel piano perpendicolare al Polo Nord. In un certo istante t₀ l’astronave A₀ e l’Italia I₀ si trovano proprio una sopra l’altra: a parte l’altezza (che nella proiezione non si vede), la loro distanza è esattamente zero. Facciamo passare tre ore (un quarto del percorso di entrambi i “contendenti”) e siamo nelle condizioni I₁ e A₁. Beh… è indubbio che la distanza d1 non è più zero e che l’astronave si sta allontanando dal nostro Bel Paese.

La situazione diventa ancora più rilassante dopo altre tre ore: l’astronave è in A₂ e la sua distanza, sul piano del foglio, è diventata proprio il raggio della circonferenza su cui sta girando l’Italia, che si trova in I₂. A questo punto, però, le cose cambiano…

Dopo altre tre ore l’Italia si viene a trovare in I₃, mentre l’astronave in A₃. Accidenti, la distanza è tornata come quando eravamo in I₁, ossia sta diminuendo. La catastrofe (se così vogliamo chiamarla) capita quando l’Italia arriva in I₄. Sono passate dodici ore dalla partenza, lo stesso tempo che l’astronave ha impiegato per arrivare in A₄. Siamo di nuovo nelle condizioni di partenza (I₀, A₀): l’astronave è tornata sopra la nostra testa!

Noi, italiani, non ci siamo accorti di aver fatto una mezza circonferenza nello stesso tempo in cui l’astronave ha compiuto la sua traversata , quindi, ci siamo considerati FERMI. In tale rappresentazione l’astronave è sembrata proprio allontanarsi per poi tornare indietro. E’ un po’ come se avessimo sparato con una pistola e poi, facendo un altro percorso, fossimo arrivati a incontrare il proiettile ancora in volo: un suicidio molto particolare…

Torniamo ai nostri sistemi e applichiamo il metodo consigliato precedentemente, per disegnare ciò che si vede in un sistema rotante. In altre parole la congiungente Italia-Polo Nord deve rimanere sempre la stessa. Una costruzione molto simile (e anche più facile) di quella necessaria a descrivere la traiettoria di una palla rotante a cui abbiamo tagliato la corda che la faceva girare attorno a un centro fisso. Attraverso questa descrizione, sarà ancora più semplice tornare al quiz precedente e capire le varie manovre che avevamo eseguito.

Utilizziamo la Fig. 2.

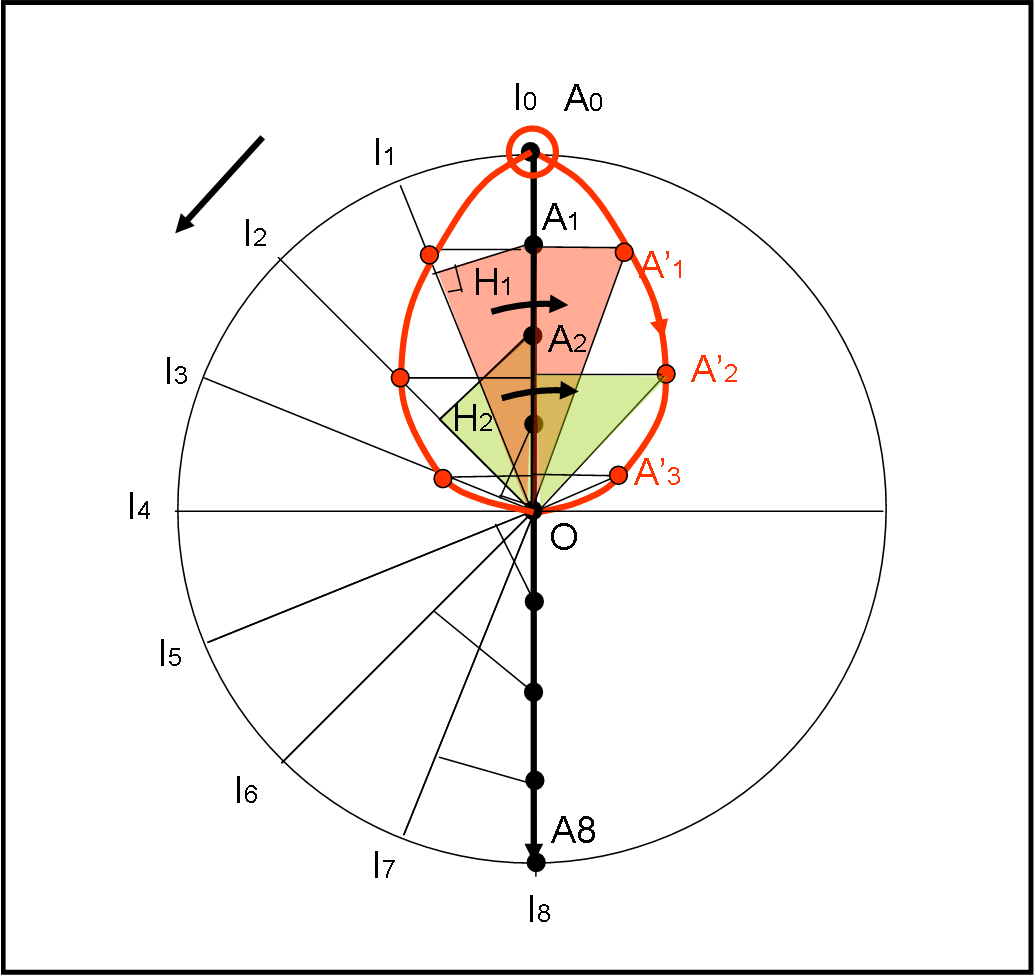
Per costruire meglio la traiettoria descritta dall’astronave nel sistema rotante dell’Italia, utilizziamo intervalli di tempo (e quindi angolari) minori di tre ore, ad esempio un’ora e mezza (ossia 180°/8 = 22.5°). In altre parole, abbiamo diviso il viaggio dell’astronave in 8 intervalli (punti neri), così come quello dell’Italia.

Vediamoli nel sistema fisso di un alieno, dove abbiamo chiamato O il Polo Nord (l’unico punto che resta fermo in entrambi i sistemi). Ogni intervallo angolare percorso dall’Italia va da 1 a 8, così come le posizioni dell’astronave. Come si vede bene (da un sistema fisso esterno), l’Italia, dopo 12 ore (I₈), coincide con l’astronave nel suo punto finale A₈. Avremmo già risolto il problema di partenza (si sono di nuovo incontrate!), ma a noi interessa, adesso, vedere come appare la traiettoria dell’astronave dall’Italia considerata ferma nel suo sistema rotante. Solo così vedremo agire l’accelerazione di Coriolis…

Ne consegue che, praticamente, prima dobbiamo utilizzare la posizione relativa tra Italia e astronave nel sistema inerziale fisso e poi far coincidere il punto relativo all’Italia con quello iniziale. Se in questo caso, la faccenda è quasi ridicola, non lo sarà più per movimenti meno semplici… fidatevi!

Cominciamo a considerare l’Italia nel punto I₁. Nello stesso istante l’astronave coincide con il punto A₁. Cosa dobbiamo fare adesso? Considerare l’asse OI₁ come nuovo asse del sistema rotante rispetto a cui riferire la posizione dell’astronave. Basta allora tracciare la perpendicolare dal punto A₁ al l’asse OI1. Per riportare il tutto nelle condizioni iniziali, dobbiamo far coincidere A₁ con A₀ (pallino rosso grande), ossia dobbiamo far ruotare il triangolo OH₁A₁ verso destra fino a far coincidere A₁ con A₀. Ne segue che il punto A₁ si sposta in A’₁. Questo è il primo punto del percorso dell’astronave visto da A₀, considerato fermo. Stiamo costruendo, lo ripetiamo, la traiettoria dell’astronave come viene vista dall’Italia considerata ferma e sempre coincidente con I₀.

Non ci resta che proseguire con questo giochino, spostandoci  nel nuovo asse OI₂: Nello stesso istante l’astronave si è portata in A₂. Tracciamo da A₂ la perpendicolare a OI₂ e otteniamo il nuovo triangolo rettangolo verde IH₂P₂. Solita rotazione verso destra fino a che I₂ coincida con I₀ e il gioco è fatto: abbiamo trovato A’₂. Per non pasticciare troppo la figura continuiamo a ripetere il meccanismo fino ad arrivare nel punto O, dove giunge anche l’astronave A₄ e dove si posiziona anche A’₄.

L’astronave continua ad andare verso il basso, mentre l’Italia continua a girare in senso antiorario. Poco male, continuiamo a tracciare le perpendicolari dai punti relativi all’astronave agli assi rotanti che congiungono il centro con l’Italia. Ci accorgiamo subito che la faccenda è perfettamente simmetrica a prima e che, riportando gli assi sopra quello iniziale I₀O, si ottiene una curva simmetrica a quella dell’andata, rispetto all’asse iniziale Italia-Polo Nord (I₀O).

Eh sì, è proprio vero… L’astronave torna verso l’Italia (che si considera FERMA), descrivendo una curva (Coriolis non perdona) molto interessante e forse inaspettata.

Teniamo conto di una semplificazione che abbiamo fatto: abbiamo considerato la distanza, tra Italia e astronave, solo nel piano del foglio (come se la Terra fosse piatta), ma a noi interessava proprio questa distanza e quindi nessun problema per il risultato finale.

Esistono altri molti modi di agire per ottenere la curva finale. Noi abbiamo usato quello più “classico”, ossia che lavori con coordinate cartesiane (in pratica, i nostri triangoli hanno come cateti le coordinate dei punti dell’astronave rispetto a due assi che continuano a ruotare), ma potevamo anche sbizzarrirci, considerando altre coordinate. Tuttavia, consiglio di usare sempre questo metodo in quanto le cose diventeranno più ingarbugliate quando si cambieranno le traiettorie dell’astronave e/o quando cambierà la sua velocità.

A questo punto, direi che non vi sono più problemi teorici nel costruire nuovamente la traiettoria dell’astronave, dimezzando la sua velocità. Bisogna stare bene attenti a non confondersi e a utilizzare sempre punti e assi rotanti corrispondenti, oltre a tenere conto che le coordinate di riferimento possono diventare negative. Tuttavia, se ruotiamo nel giusto verso e della giusta “quantità”, non vi sono veri problemi: l'importante è che l'asse rotante vada a coincidere con quello di partenza, ruotando  il tutto(sia a destra che a sinistra, come si preferisce e/o come risulta più immediato).

Provate a svolgere il nuovo “compitino”, l’ultima domanda del quiz precedente, seguendo questa trattazione molto semplice, ricordando però di  mantenere fissa la congiungente Italia-Polo Nord, ossia I₀O. La nostra astronave ci farà spaventare solo per poco tempo e poi tireremo un sospiro di sollievo…

La Fig. 3 riassume il risultato in modo molto rapido (aumentando i punti, la curva si costruirebbe molto meglio, come hanno fatto Arturo e Andy).

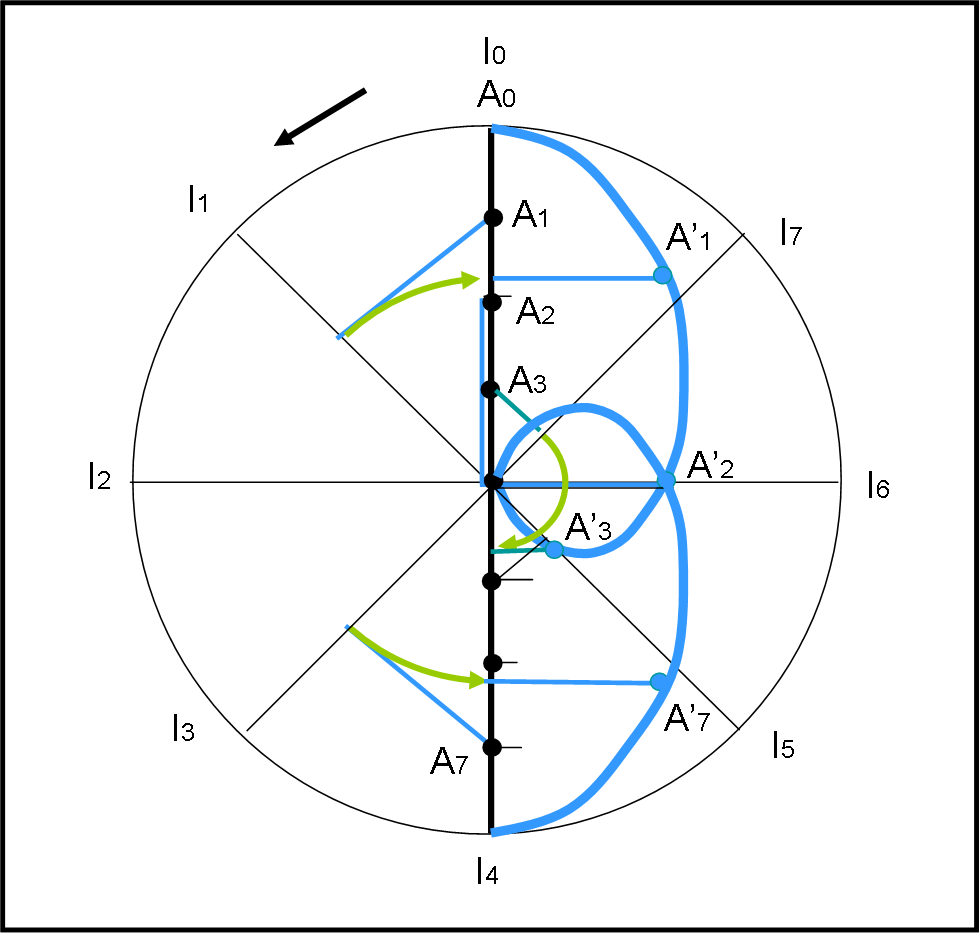
In essa ho costruito solo alcuni punti, disegnando in verde le frecce che servono a riportare l'asse rotante nella posizione originaria. Come si vede bene, dopo le 12 ore percorse dall'Italia, si può benissimo invertire il senso della freccia, dato che l'importante è tornare alle origini. Provate a farlo da soli, seguendo le tracce riportate nella figura: sarà molto istruttivo e divertente e, alla fine, si sarà acquisita la competenza e la sicurezza necessarie per affrontare anche qualcosa di più complicato.

Io la butto lì... ma qualcuno potrebbe provare a costruire la traiettoria per un'astronave che riduce ancora di più la sua velocità (ad esempio, impiegando 36 o 48 ore ad attraversare la Terra). Roba da far "girare" la testa...

Bando agli alieni più o meno veloci (che ci hanno aiutato molto a immaginarci fissi in un sistema non inerziale e a guardare in faccia gli effetti dell'accelerazione di Coriolis), la prossima volta proseguiremo verso  effetti più plateali ed evidenti.

N.B.: mi raccomando, se vi sono restati ancora dei dubbi, non abbiate paura a dirlo nei commenti. Tutti dobbiamo imparare e le vostre richieste pubbliche serviranno sicuramente anche a molti altri, che temono di uscire allo scoperto, e a me, per imparare a spiegare ancora meglio. Inoltre, se qualcosa è ancora restato nel vago, sorgeranno grossi problemi nel proseguire con il nostro simpatico Coriolis.